抛物线是极限状态的椭圆
张青山,李凤清(四川职业技术学院应用数学与经济系,四川 遂宁 629000)
抛物线是极限状态的椭圆
张青山,李凤清
(四川职业技术学院应用数学与经济系,四川遂宁629000)
本文给出结论:抛物线y2=2px(p>0)是椭圆+=1(a>p>0)当a趋于正无穷大时的极限状态.并举例说明如何从由椭圆的性质来探求抛物线的性质.
抛物线;椭圆;极限;性质;探究

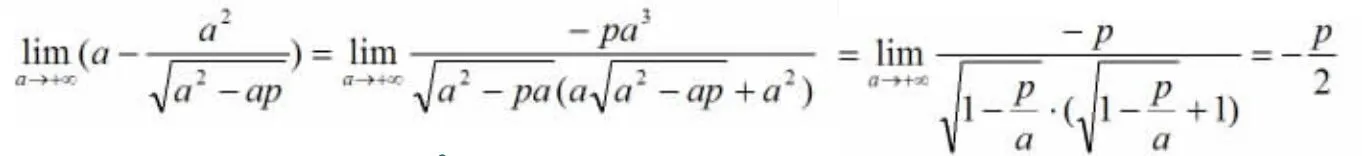
因此我们说,抛物线y2=2px(p>0)是椭圆+=1(a>p>0)当a趋于正无穷大时的极限状态.故我们可以把抛物线y2=2px(p>0)描述为一个长半轴为a,短半轴为,中心为(a,0),左焦点为(,0),右焦点为(2a-,0),左准线为x=-,右准线为x=2a+,且a为无穷大的椭圆.那么椭圆与抛物线应该具有一些共性,我们就可以运用类比的方法从椭圆的一些性质来探求抛物线的性质.下面略举几例.
1椭圆的光学性质为:由椭圆的一焦点射向椭圆上任一点的光波或声波,经该椭圆反射后会经过另一焦点.由于抛物线是极限状态的椭圆,其另一焦点在焦点所在对称轴上的无穷远点,即可推出抛物线的光学性质:由抛物线的焦点射向抛物线上任一点的光波或声波,经该抛物线反射后会沿平行于抛物线的对称轴射出.
2由文[1]命题一可得椭圆的一个性质:P(x0,y0)是椭圆+=1(a>p>0)上任意一点,PA,PB是两条互相垂直的弦,则动弦AB过定点
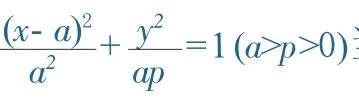
收稿日期:2015-05-28
作者简介:张青山(1962-),男,四川蓬溪人,四川职业技术学院副教授。研究方向:初等数学,数学教育。
抛物线的性质1(文[1]命题二):P(x0,y0)是抛物线y2=2px(p>0)上任意一点,PA,PB是两条互相垂直的弦,则动弦AB过定点P′(2p+x0,-y0).
由于抛物线y2=2px(p>0)是椭圆+
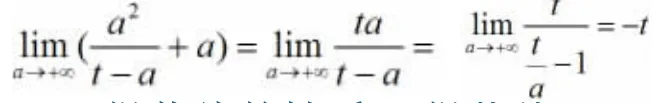
抛物线的性质2:抛物线y2=2px(p>0),过x轴上的定点P(t,0)(t>0)的直线交抛物线于A,B两点,以点A,B为切点分别作抛物线的切线,它们交于点C,则C必在直线x=-t上.
4.大家知道,圆有一个简单性质:对圆O及其圆O中异于圆心的定点P,过点P的弦AB与圆围成的弓形面积最小时,必然有PA=PB.
我们将圆O通过压伸变换成为椭圆,根据压伸变换不改变线段比、不改变面积比的性质即可得到下面结论.
椭圆的性质:对椭圆及其椭圆内异于中心的定点P,过点P的弦AB与椭圆围成的弓形面积最小时,必然有PA=PB.
由于抛物线是极限状态的椭圆,我们可得出下面结论.
抛物线的性质3:对抛物线及其抛物线内的定点P,过点P的弦AB与抛物线围成的弓形面积最小时,必然有PA=PB.
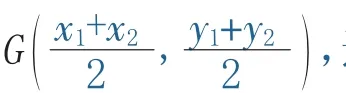
我们也可以说,抛物线y2=2px(p>0)是双曲线(x
a-2a)2-ayp2=1(a>0,p>0)的实半轴a趋近于正无穷大时的极限状态.本文对此不作赘述.
[1]季福根.圆锥曲线中伴随曲线与相关点线问题再探讨[J].数学通报,2013,(11).
责任编辑:张隆辉
G 633.6
A
1672-2094(2015)04-0167-02椭圆C+=1(a>p>0)的中心为(a,0),左焦点为(a-,0),右焦点(a+,0),左准线方程为x=a-,离心率为.
——对2018年广州市一道中考题的研究

