古塔的变形趋势数学模型

刘中宁（遂宁中学校，四川　遂宁　629000）

古塔的变形趋势数学模型

刘中宁
（遂宁中学校，四川遂宁629000）

本文要解决古塔各层中心位置坐标的通用求法，用数量关系刻画该塔倾斜、弯曲、扭曲的变形情况，还要分析该塔的变形趋势这些问题.我们用每层测得的数据作多元线性回归拟合，通过M atlab软件和Excel编程计算，得到各层的平面方程，在此平面上，用与到各测量点的距离相等的点建立超定方程求出层中心.用各层平面法向量分别对z轴的倾斜角、在oxy平面内的方位角、与x轴的方向角、与y轴的方向角来刻画倾斜和扭曲和用每三层层中心点所确定圆的曲率这些量各自的最大值来刻画倾斜、扭曲和弯曲程度，也可用各量的相对偏移量来表述.用各量4次测量计算的数据进行二次曲线拟合来描述古塔变形的变化趋势.

多元线性回归拟合；超定方程；初等数学模型；最大值

1　问题

某古塔已有上千年历史，是我国重点保护文物.管理部门委托测绘公司先后于1986年7月、1996年8月、2009年3月和2011年3月对该塔进行了4次观测.讨论以下问题：

1.给出确定古塔各层中心位置的通用方法，并列表给出各次测量的古塔各层中心坐标.

2.分析该塔倾斜、弯曲、扭曲等变形情况.

3.分析该塔的变形趋势.

2　问题分析

问题1：计算古塔各层中心位置.

我们用每层测得的数据作多元线性回归拟合，得到的线性函数就是该层的平面方程，在此平面上，用与到各测点的距离相等的点就是层中心.

问题2：古塔倾斜、弯曲、扭曲的刻画.

我们用各层平面法向量分别对z轴的倾斜角、在oxy平面内的方位角、与x轴的方向角、与y轴的方向角来刻画倾斜和扭曲和用每三层层中心点所确定圆的曲率这些量各自的最大值来刻画倾斜、扭曲和弯曲程度.由于前后各两次采集的数据应该分别是同一测位，我们分成两组比较各自的量差，得到偏移度，它们可以直观地反映出古塔倾斜、弯曲、扭曲的变形特征.

问题3：古塔的变形趋势.

我们分析上述四个时间段的相关量的最大值的变化规律，分别用曲线拟合来预测古塔的变形趋势.

3　模型假设

1、假设古塔的变形只受自然因素影响，不受人为影响.

2、假设古塔在1000年前基底是水平的，没有倾斜、弯曲、扭曲的任何变形.

3、假设每次的测量误差在允许精度范围内.

4　符号说明

r,R:圆的半径.α：直线的倾角.θ：直线的方位角.β：直线的轴向角.K:曲线的曲率.t:时间.

5　模型建立与求解

查阅有关参考书籍，设各层测点的坐标Mi(xi,yi,zi)i=1，2…m,中心位置坐标P(a,b,c)，平面的动点坐标M(x,y,z).

收稿日期:2015-06-24

作者简介：刘中宁（1976-），男，四川遂宁人，四川省遂宁中学校中学一级教师.

对于问题1，我们建立各层测点的平面方程数学模型：

由于这些点不全在一个平面上，因此用多元线性回归拟合方法求出系数A，B和C的值，同时求得层平面的法向量n軋=(B,C,-1).

在所求的平面上求出到各测点的距离相等的点的坐标，它就是各层面的中心坐标，建立如下数学模型：

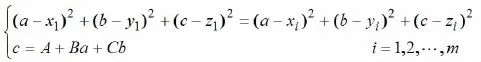
简化上述模型得：

解关于a、b、c的超定方程，得到层面中心位置坐标。

表5.1

?

对于问题2，我们由层平面法向量求关于z轴的倾斜角、oxy平面的方位角、与x轴的方向角和与y轴的方向角的数学模型：

取古塔相邻层面三个中心点Pi(ai,bi,ci),i=1,2,3作一个三角形，其三边的长度分别是e、f、g，用外接圆的半径的倒数来近似代替古塔的弯曲程度，数学模型如下：

代入相关数据求出各量测了四次的最大值和两组的偏移值。

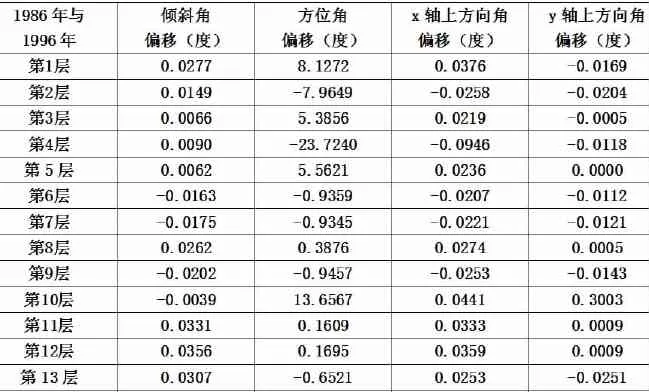
表5.2

对于问题3，以时间为自变量，以问题2中求得各量的最大值为函数，为了预测古塔的变化，我们建立数学模型是：

y=a+bx+cx2

作曲线拟合求出拟合函数，通过计算数值或作图，来预报古塔的变形.

表5.3

图5.1

对于倾斜角的变化趋势，我们得到二次多项式拟合函数是α=0.00000055108737-0.00005723778793t-0. 47932928200295t2倾斜角的变化趋势如图5.1所示.

对于方位角的变化趋势，我们得到二次多项式拟合函数是θ=-0.0004391492+1.48271078t-1035.014389t2方位角的变化趋势如图5.2所示。

图5.2

图5.3

对于轴方向角的变化趋势，我们得到二次多项式拟合函数是θx=-0.000010972110+0.122235092439t-109. 856699568783t2

x轴方向角的变化趋势如图5.3所示.

对于y轴方向角的变化趋势，我们得到二次多项式拟合函数是θy=-0.000140331180+0.508784645805t-365.232291811525t2

y轴方向角的变化趋势如图5.4所示.

图5.4

图5.5

对于曲率K的变化趋势，我们得到二次多项式拟合函数是K=-0.00000185490615+0.00556761279620t-3. 68633539644t2

曲率的变化趋势如图5.5所示.

[1]马莉.MATLAB数学建模实验与建模[M].北京：清华大学出版社，2010：61-62.

[2]华信卓越.Excel2007公式、函数与图表[M].北京：电子工业出版社，2008:12-14.

[4]梁海奎.古塔变形测量方法探讨[EB/OL].[2013-09-15].http://wenku.baidu.com/view.

[5]章绍辉.数学建模[M].北京：科学出版社，2010:48,62.

责任编辑：张隆辉

TU 196.1

A

1672-2094（2015）04-0169-06