基于递归特征分析的NURBS曲线插补算法

韩　江　江本赤　夏　链　田晓青

合肥工业大学，合肥，230009

基于递归特征分析的NURBS曲线插补算法

韩江江本赤夏链田晓青

合肥工业大学，合肥，230009

在分析NURBS曲线公式中基函数递归特征的基础上，提出了一种新的NURBS曲线插补算法。该算法通过前一个参数增量值和前一段插补弦长来确定下一个参数增量值，进而实现对参数的密化。仿真实验结果表明，该算法在改善弦长误差和减小计算量方面优于Taylor展开插补算法。

NURBS曲线；递归特征；迭代算法；插补

0　引言

在CAD/CAM系统中，一般采用参数形式来表示复杂的曲线和曲面。NURBS具备很强的形状控制能力，于1991年被ISO确定为定义产品形状的唯一数学方法[1]。然而，传统的CNC系统只能进行直线和圆弧插补，需要用大量微直线段和圆弧逼近自由曲线，不仅需要大量的存储空间，而且需要很长的计算时间，这显然不符合高速加工的实时性要求。更重要的一点是用多段直线和圆弧表示曲线，段间的不连续破坏了曲线或曲面的光滑度，同时会导致速度、加速度的不连续[2]。因此，学者们对多种NURBS曲线直接插补技术进行了研究[3-6]。通过将NURBS曲线参数传递给数控系统，然后由CNC系统生成轨迹点，实现对NURBS曲线的直接插补。NURBS曲线插补就是在已知当前参数的基础上，通过合理确定参数增量值来求取下一个参数值，然后从参数空间映射到轨迹空间，下一个插补点就是将新的参数值代入数学模型而得到的。因而，NURBS曲线插补的关键在于确定下一个插补点的参数，实现参数的密化。

Bedi等[7]首先提出将曲线参数在定义域内等分的方法，该方法会造成插补速度的波动。Shpitalni等[8]针对参数曲线提出了Taylor展开近似方法的插补算法。现有文献中报道的NURBS曲线插补算法大多是基于Taylor展开公式逼近而实现插补点的参数密化的[9-14]。由于Taylor一阶逼近会产生较大的截断误差，罗福源等[10]对基于Taylor一阶展开插补法的平稳性进行了研究。Shiuh等[11]在Taylor展开近似计算的基础上考虑了曲线的几何特性，提出了闭环控制NURBS插补算法。Farouki等[12]和Yeh等[13]分别采用Taylor二阶逼近和改变速度的方法来减小插补误差。Liu等[14]提出了考虑动力学的NURBS插补算法。Feng等[15]提出了考虑轴加速度限制的NURBS实时自适应插补算法。上述考虑加减速和机床动力学的NURBS曲线插补算法也采用了Taylor二阶逼近。无论采用哪一种算法，Taylor一阶逼近都会产生较高的插补弦长误差，而Taylor二阶逼近将大大增加运算量。

事实上，通过考察NURBS曲线的定义公式不难发现，其中的B样条基函数是由递推公式定义的，存在递归特性。该特性的几何意义体现在，当相邻的两个参数增量值接近时，通过插补所得到的两个弦长值亦较接近。因此，一方面，可以通过预估的参数增量值Δu初步获取所需弦长；另一方面，尽管参数与弦长之间不存在精确的解析关系，但仍可根据初步得到的弦长值反过来对参数增量值Δu进行适当的微调，经过少量的迭代计算得到理想的参数增量值。

本文提出了一种基于NURBS自身递归特征的NURBS曲线简易插补算法。该算法通过前一个参数增量值和前一个弦长值来获取下一个插补点的参数增量值。为得到理想的弦长值，在算法中设置了过渡参数增量值，最终的有效参数增量值则是利用上述递归特征更新过渡增量值而得到的。对一条典型NURBS曲线进行的插补仿真实验验证了所提算法的可行性。

1　NURBS曲线的定义

一条p次NURBS曲线定义为

(1)

a≤u≤b

其中，Pi为控制顶点；wi为权因子；Ni,p(u)是定义在非周期节点矢量U上的p次B样条基函数，它是在区间[ui,ui+p+1)上的非零多项式，其数值为

(2)

(3)

节点矢量U中，a和b的重复度都为p+1，除非特别声明，通常取a=0，b=1。

式(2)和式(3)为B样条基函数定义公式，不难看出其具有递归特征。以定义在节点矢量U=(0，0，0，0，0.25，0.5，0.75，1，1，1，1)上的3次基函数为例，考察基函数的变化情况，如图1所示。为便于观察，图1中只给出了其部分基函数。可见，各基函数是连续的，不存在突变。

图1　某3次NURBS曲线的部分基函数

当Δu=0.005时，取相邻两基函数的差值ΔNi,p(u)=Ni,p(u)-Ni-1,p(u)，可以更清楚地观察基函数的变化情况，如图2所示。可见，基函数的递归特征决定其变化的平滑性，因而利用递归特征求取均匀的插补弦长存在理论上的可行性。

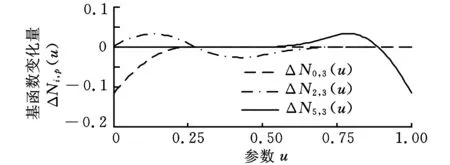
图2　相邻基函数的变化量

2　基于递归特征的NURBS曲线插补算法

NURBS曲线插补的关键在于求取下一个插补点对应的参数，而轨迹插补算法就是实现参数u在节点矢量区间上的密化。针对Taylor展开算法的不足，为减小运算量和改善插补弦长误差，本文提出了基于NURBS自身递归特征的插补算法。

2.1求取初始参数增量Δu1的算法

设节点区间为0≤u≤1，即umin=0，umax=1。按照递归特征求取参数增量值，需要前一个参数增量值和前一段插补弦长，但是用这种方法显然无法求出第一个参数增量值Δu1。考虑到当参数u从0增大到1时，就完成了对整个NURBS曲线的插补，即当参数的变化量为Δut=umax-umin时，弧长的变化量为NURBS曲线的总弧长Lt。设期望弦长值为Ld，可尝试用Δut∶Lt=Δu1∶Ld这个比例关系来初步求出Δu1。但是由于计算弧长Lt比较复杂，经分析NURBS曲线的有关参数信息，本文拟利用控制点之间的距离总长Lk(即控制多边形的总边长)代替Lt来初步求出Δu1，所产生的误差可以通过较简单的迭代计算来消除。Lk的计算公式为

(4)

式中，xP(i)、yP(i)为控制顶点Pi的坐标值。

由于Lt与Lk之间存在较大误差，将此处所求出的参数增量值称为过渡参数增量值，记作Δu1,1，其计算公式为

Δu1,1=ΔutLd/Lk

(5)

同理，记过渡参数值u2,1=u1+Δu1,1，利用NURBS公式求出过渡插补点C(u2,1)之后，可得到首个过渡弦长L1,1=|C(u2,1)-C(u1)|。将L1,1与期望弦长Ld之间相对误差率记为ε1，其表达式为

ε1=(Ld-L1,1)/Ld

(6)

记给定的许用相对误差为[εL]，当ε1>[εL]时，则需求出第2次过渡参数增量值，按照下式进行1次迭代计算(为了明确算法的计算量，将使用NURBS公式的次数称作迭代次数)：

Δu1,1=Δu1,1Ld/L1,1

(7)

同理，可得到过渡参数值u2,2=u1+Δu1,2和过渡弦长L1,2=|C(u2,2)-C(u1)|，并求出相对误差ε2。则求取初始参数增量值的通式为

Δu1,k=Δu1,k-1Ld/L1,k-1k≥2

(8)

连续应用式(8)，直到弦长相对误差满足要求为止，而此时的过渡值即为最终的有效值。即当εk≤[εL]时，Δu1,k=Δu1，u2,k=u2，L1,k=L1。计算Δu1所需迭代次数的确定方法将在实验仿真部分详细说明。

2.2求取其余参数增量Δui(i>1)的算法

按照上述对递归特征的分析，当两个参数增量值大小接近时，所得到的两弦长值也比较接近，即当Δui-1≈Δui时，Li-1≈Li，反之亦然。因此，可以通过期望弦长值反求Δui。上文已经求出了Δu1和u2，其余的插补点参数为ui+1=ui+Δui(i>1)，其中的参数增量Δui,1的计算公式为

Δui,1=Δui-1Ld/Li-1

(9)

类似于式(8)，通过m-1次迭代求取其余参数增量值的通式为

Δui,m=Δui,m-1Ld/Li,m-1m≥2

(10)

当εm≤[εL]时，Δui,m=Δui。特别地，当ui>umax时，取ui=umax。计算Δui(i>1)所需迭代次数的确定方法也将在实验仿真部分说明。

3　仿真实验与分析

为了验证本文算法的可行性并评估其性能，现以节点矢量U=(0,0,0,0,0.1,0.2,0.3,0.4,0.5,0.6,0.8,0.9,1,1,1,1)，控制顶点的坐标分别为(2.0,8)mm，(3.0,4.8)mm，(4.0,3.0)mm，(5.0,2.0)mm，(6.2,2.5)mm，(7.5,8.8)mm，(9.0,8.5)mm，(10.5,7.0)mm，(11.0,5.0)mm，(13.5,0)mm，(16.0,5.5)mm，(18.0,7.0)mm，wi=1，p=3的NURBS曲线为例进行仿真实验。如果将期望弦长设为恒定值，则利用本文算法所获得的插补点分布情况如图3所示。

图3　期望弦长设为恒定值时的插补点分布示意图

3.1迭代次数的确定

3.1.1确定计算Δu1所需迭代次数

第一个参数增量Δu1的求解，由于没有前一段弦长值可供参考，本文参照了NURBS曲线控制多边形的边长值，虽然会产生较大的弦长相对误差，但可通过后续的迭代计算来改善。为了控制误差范围，设置许用弦长误差率[εL]作为迭代计算的判断依据，即当前一次计算所得弦长的误差率超过[εL]时，就需进行下一次迭代计算。下面的仿真实验是按照2.1节所述的计算方法开展的。

实验结果表明，当期望弦长Ld=0.1mm时，未经迭代计算(仅根据控制多边形的边长值按比例求解)所得的过渡参数增量Δu1,1=2.9067×10-3，弦长误差率ε1=186.46%；经1次迭代计算后的Δu1,2=1.0147×10-3，弦长误差率ε2=1.33%；迭代2次所得的Δu1,3=1.0013×10-3，弦长误差率则降至ε3=0.01%。可见，对于该NURBS曲线，若设[εL]=2%作为控制条件，则只需进行1次迭代；若设[εL]=1%，则需进行2次迭代。

当期望弦长Ld=1μm时，未经迭代计算所得的Δu1,1=2.91×10-5，ε1=192.29%；经1次迭代计算后的Δu1,2=9.9445×10-6，而弦长误差率降至ε2=0.01%；迭代2次所得的Δu1,3=9.9432×10-6，弦长误差率则骤降至ε3=10-8。显然，当期望弦长值为μm级时，若以[εL]=1%作为控制条件，则只需进行1次迭代，而即使[εL]=0.1%，迭代2次已经足够。

作为首个参数增量，Δu1的精确度将影响后续参数增量Δui(i>1)计算的迭代效率。因此，必要时可以考虑减小[εL]值以适当增加迭代计算的次数，但是3次迭代已经能获得足够高的精度。

3.1.2确定计算Δui(i>1)所需迭代次数

对照上文计算Δu1的方法，来探究求解Δui(i>1)所需的迭代次数，仍分别取Ld=0.1mm和Ld=1μm进行实验。为了表征弦长值的波动情况，特引入标准差σ，其计算公式如下：

(11)

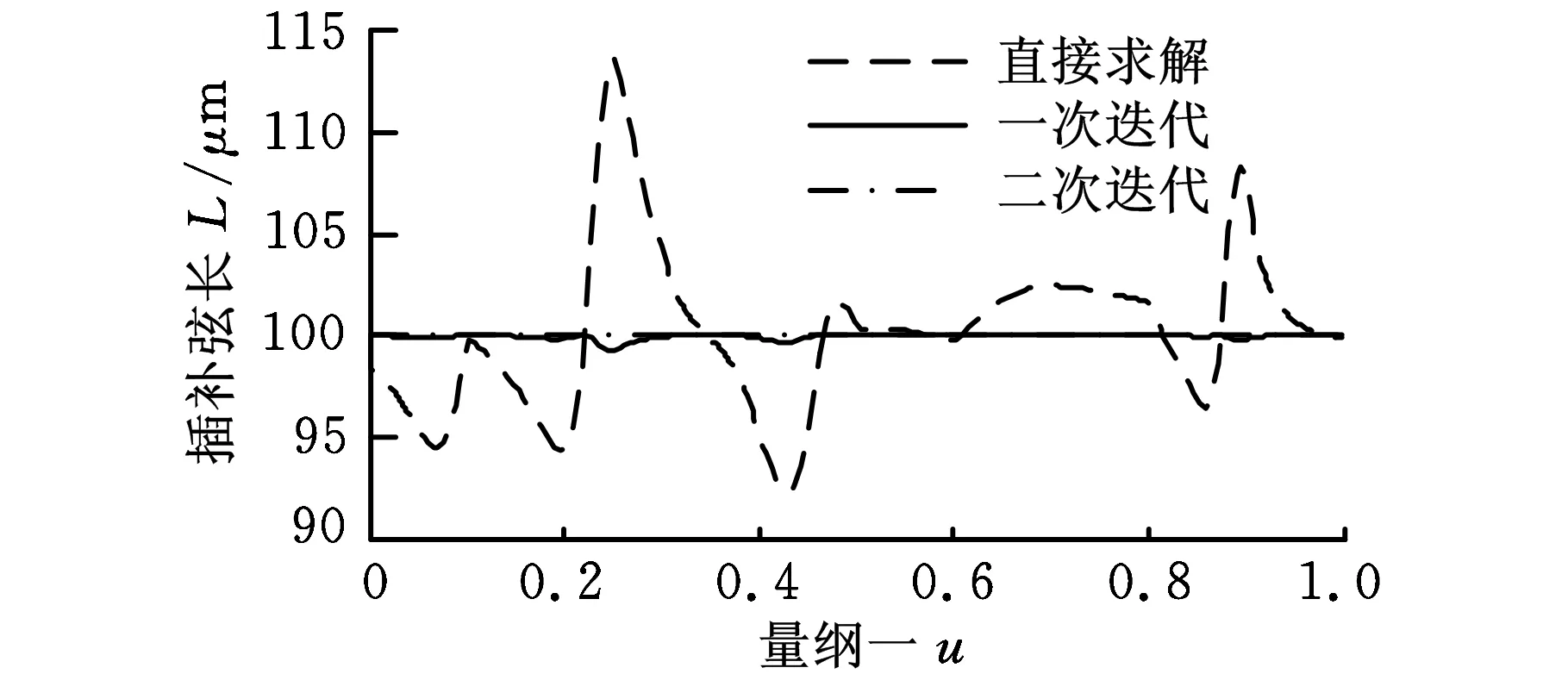
图4　Ld=0.1 mm时的插补弦长变化情况

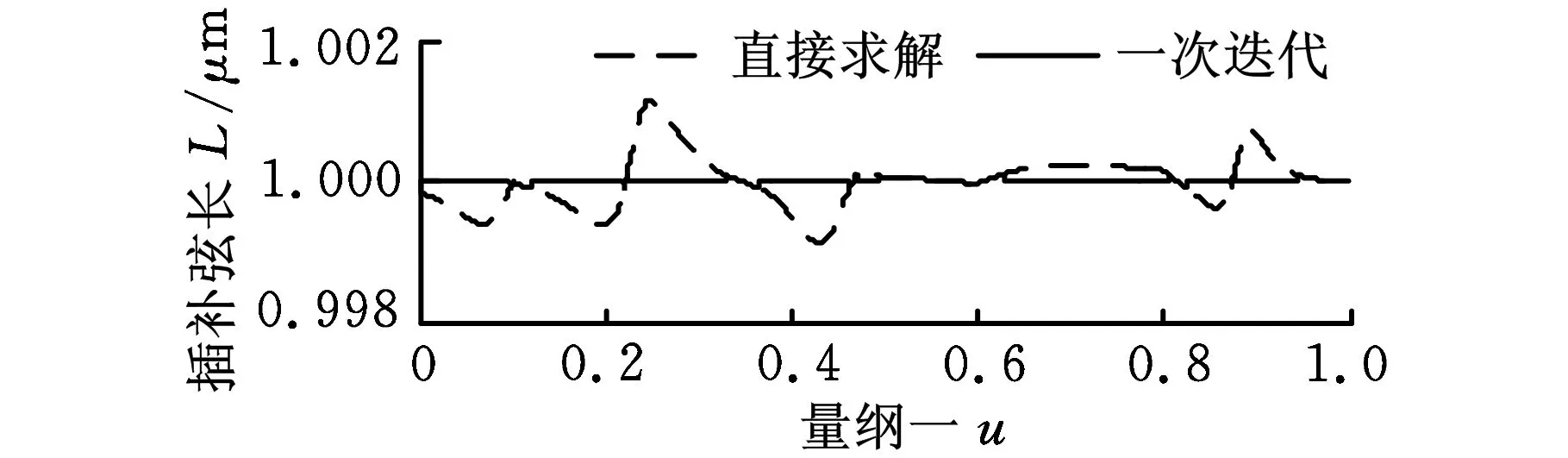
图5　Ld=1 μm时的插补弦长变化情况

综合图4和图5可见，在同等弦长误差率限制条件下，期望弦长Ld越小，求解参数增量Δui所需的迭代次数越少，当Ld为μm级时，未经迭代计算而根据递归特征直接求解即可得到非常高的计算精度。

3.2误差分析

曲线插补的误差一般分为径向误差和弦高误差。对于本文所提出的直接插补算法，由于插补点都是通过NURBS公式直接计算出来的，即所有插补点都落在曲线上，不存在径向误差。其弦高误差Ei计算公式为

(12)

式中，ri为第i个插补点C(ui)处的曲率半径；Li为第i段插补弦长。

由式(12)可以看出，当弦长值Li很小时，Ei也很小。以本文所用的NURBS曲线为例，其曲率分布情况如图6所示，当u=0.224时，曲率半径取得最小值rmin=0.559mm，此时的弦高误差Ei将达到最大值Emax。当Li=Ld=0.1mm时，Emax=2μm；当Li=Ld=1μm时，Emax=0.2236nm。

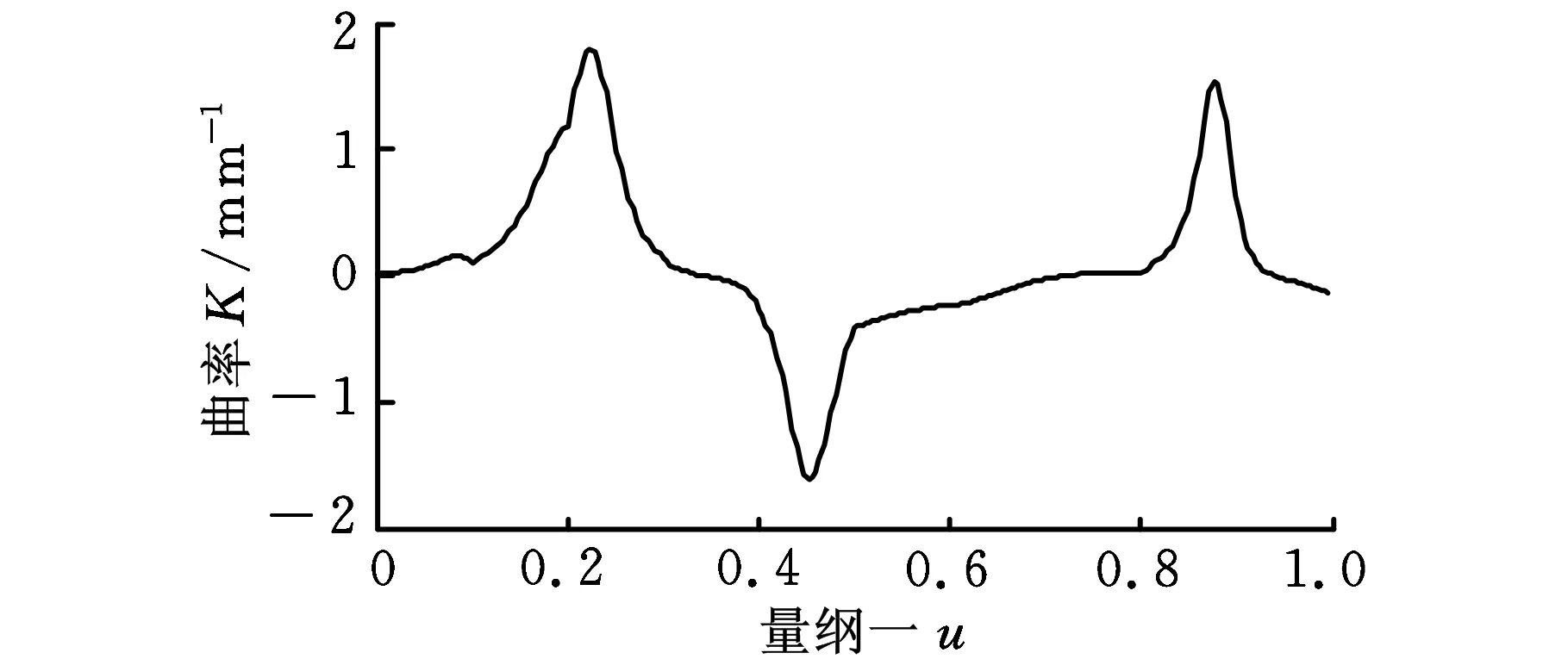
图6　NURBS曲线曲率分布图

可见，当期望弦长为μm级时，本文算法产生的弦高误差与目前数控机床的分辨率相比，完全可以忽略。

3.3与泰勒展开方法对比

为了进一步验证本算法的性能，从运算量和插补弦长误差两个方面，将其与常用的Taylor展开系列算法进行对比。

3.3.1插补运算量的比较

Taylor二阶展开插补算法常用的公式为

而本算法中当迭代次数为2次以上(m≥2)时所用的公式为

Δui,m=Δui,m-1Ld/Li,m-1

显然本算法极大地减少了运算量，更易于满足高速插补的实时性要求。

3.3.2插补弦长误差的比较

仍以图3所示的NURBS曲线为例，设置期望弦长Ld=0.1 mm，比较两种算法插补运算的弦长误差情况。

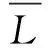
图7　一阶Taylor展开与一次迭代计算效果对比

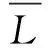
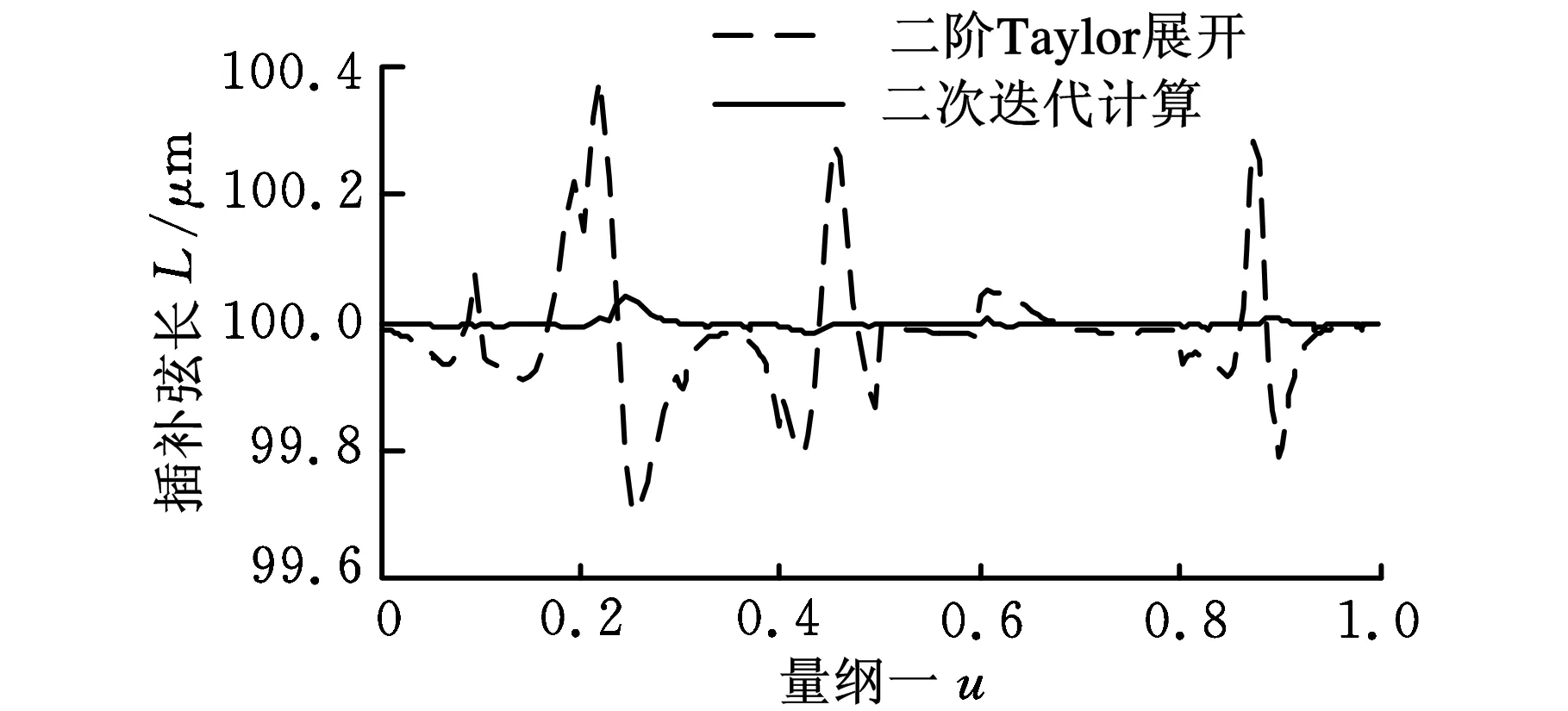
图8　二阶Taylor展开与二次迭代计算效果对比

结果表明，与Taylor展开系列算法相比，本算法不仅运算量小，而且弦长误差也更小，总体上优于基于Taylor展开的插补算法。

4　结语

在分析NURBS自身递归特征的基础上，本文提出了一种新的NURBS曲线插补算法。该算法通过前一段插补弦长和前一个参数增量的关系来获取下一个插补点对应的参数。实验结果表明：①通过利用NURBS公式进行少量的迭代计算可显著改善插补的弦长误差，并可根据所设置的精度自动调整迭代次数；②在运算量相当的条件下，期望弦长越短，插补效率越高，当期望弦长值为μm级时，未经迭代计算而根据递归特征直接求解亦可得到极高的插补精度，而且弦高误差也足够小。

由于该算法避免了复杂的NURBS曲线求导运算，代之以简单的四则运算，故其计算量远小于基于Taylor展开的系列算法，改善了插补的实时性。而且该算法插补弦长的标准差也小于Taylor展开算法，可以更有效地抑制插补速度的波动。

[1]王田苗,曹宇男,陈友东,等.基于de Boor算法的NURBS曲线插补和自适应速度控制研究[J].中国机械工程，2007,18(21):2608-2613.

Wang Tianmiao, Cao Yunan, Chen Youdong, et al. NURBS Interpolation and Feedrate Adaptive Control Based on de Boor Algorithm[J].China Mechanical Engineering, 2007, 18(21):2608-2613.

[2]叶佩青,赵慎良.微小直线段的连续插补控制算法研究[J].中国机械工程,2004,15(15):1354-1356.

Ye Peiqing, Zhao Shenliang. Study on Control Algorithm for Micro-line Continuous Interpolation[J].China Mechanical Engineering, 2004, 15(15):1354-1356.

[3]赵国勇,徐志祥,赵福令.高速高精度数控加工中NURBS曲线插补的研究[J].中国机械工程,2006,17(3):291-294.

Zhao Guoyong, Xu Zhixiang, Zhao Fuling.Study on NURBS Curve Interpolator in the High Speed and High Accuracy CNC Machining[J].China Mechanical Engineering, 2006, 17(3):291-294.

[4]游有鹏,王珉,朱剑英.NURBS曲线高速高精度加工的插补控制[J].计算机辅助设计与图形学学报, 2001, 13(10): 943-947.

You Youpeng, Wang Min, Zhu Jianying. An Interpolator for NURBS Curve Machining with High Speed and High Accuracy[J].Journal of Computer-Aided Design & Computer Graphics, 2001, 13(10): 943-947.

[5]Nam S H, Yang M Y.A Study on a Generalized Parametric Interpolator with Real-time Jerk-limited Acceleration[J]. Computer-Aided Design, 2004, 36(4): 27-36．

[6]彭芳瑜,何莹,罗忠诚,等.NURBS曲线机床动力学特性自适应直接插补[J].华中科技大学学报(自然科学版),2005,33(7):80-83.

Peng Fangyu, He Ying, Luo Zhongcheng, et al. NURBS Curve Interpolation Algorithm with the Adaptation to Machine Tool Kinetic Character[J]. J. Huazhong Univ. of Sci. & Tech. (Nature Science Edition), 2005,33(7):80-83.

[7]Bedi S, Ali I, Quan N. Advanced Techniques for CNC Machines[J].Journal of Engineering for Industry, 1993, 115(3): 329-336.

[8]Shpitalni M, Koren Y, Lo C C.Real-time Curve Interpolators[J]. Computer-Aided Design, 1994, 26(11): 832-838．

[9]刘宇,戴丽,刘杰,等. 泰勒展开NURBS曲线插补算法[J].东北大学学报(自然科学版)，2009，30(1)：117-120.

Liu Yu, Dai Li, Liu Jie, et al. Study on NURBS Interpolator with Taylor Expansion[J].Journal of Northeastern University (Natural Science)，2009，30(1)：117-120.

[10]罗福源,游有鹏,尹娟.NURBS曲线泰勒展开插补法的平稳性与改进研究[J].中国机械工程, 2012, 23(4):383-388.

Luo Fuyuan, You Youpeng, Yin Juan. Research on Stability and Improvement of Taylor-Expansion-Based Approach for NURBS Curve Interpolation[J].China Mechanical Engineering, 2012, 23(4):383-388．[11]Shiuh S, Hsu P. Adaptive-feedrate Interpolation for Parametric Curves with a Confined Chord Error[J].Computer-Aided Design, 2002, 34(3):229-237.

[12]Farouki R T, Tsai Y F．Exact Taylor Series Coefficients for Variable-feedrate CNC Curve Interpolators[J].Computer-Aided Design, 2001, 33(2): 155-165．

[13]Yeh S, Hsu P.The Speed-controlled Interpolator for Machining Parametric Curves[J]. Computer-Aided Design, 1999, 31(1): 349-357.

[14]Liu X B, Ahmad F, Yamazaki K, et al. Adaptive Interpolation Scheme for NURBS Curves with the Integration of Machining Dynamics[J].International Journal of Machine Tools and Manufacture, 2005, 45(4/5):433-444.

[15]Feng J C, Li Y H,Wang Y H,et al. Design of a Real-time Adaptive NURBS Interpolator with Axis Acceleration Limit[J].The International Journal of Advanced Manufacturing Technology,2010,48(1/4): 227-224.

(编辑陈勇)

NURBS Curve Interpolation Algorithm Based on Recursive Feature Analysis

Han JiangJiang BenchiXia LianTian Xiaoqing

Hefei University of Technology,Hefei,230009

Based on the recursive feature analysis of the base function in NURBS formula, a novel interpolation algorithm was put forwards. The method obtained the next parameter increment by a previous parameter increment and a previous chord length, and then the parameter interpolation was achieved.Simulation results show that, the proposed interpolation algorithm has obvious advantages in improving chord length errors and lessening computation load compared with those using Taylor’s equation.

NURBS curve；recursive feature；iterative algorithm；interpolation

2013-09-12

国家自然科学基金资助项目(51275147)

TP273< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.01.019

韩江，男，1963年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。主要研究方向为先进制造技术、数控技术与数控装备。发表论文100余篇。江本赤，男，1979年生。合肥工业大学机械与汽车工程学院博士研究生。夏链，女，1964年生。合肥工业大学机械与汽车工程学院教授。田晓青，女，1987年生。合肥工业大学机械与汽车工程学院讲师。