交叉杆并联机床结构参数优化
方喜峰 张思崇 许钦桓 汪通悦 刘远伟 陈小岗
1.江苏科技大学,镇江,212003 2.淮阴工学院,淮安,223001
交叉杆并联机床结构参数优化
方喜峰1张思崇1许钦桓1汪通悦2刘远伟2陈小岗2
1.江苏科技大学,镇江,2120032.淮阴工学院,淮安,223001
增大工作空间和提高灵巧度是并联机床设计的一项重要任务。依据运动学反解,采用三维搜索的方法得到了带约束条件的交叉杆并联机床的工作空间;利用自然坐标法推导了该机床的新型雅可比矩阵;基于工作空间和新型雅可比矩阵获得了交叉杆并联机床的灵巧度分布。在此基础上分析了机床各结构参数对工作空间和全域灵巧度指数的影响规律,然后用最小二乘法进行曲线拟合并以工作空间指数和全域灵巧度指数为优化目标对该机床进行优化,与优化前相比,两项指标分别增大了0.40倍和0.26倍,达到了机构优化的目的。
交叉杆并联机床;工作空间;新型雅可比矩阵;全域灵巧度指数;结构参数优化
0 引言
交叉杆并联机床的动平台采用上下两层结构,6个顶点交叉布置,具有中心对称性好、结构刚度高的优点,但同时也牺牲了部分工作空间、降低了运动灵巧性。因此,适当增大工作空间、提高灵巧度是交叉杆并联机床设计的一项重要任务。并联机构工作空间解析求解很大程度上依赖机构位置解的研究成果,至今仍没有完善的方法,目前主要还是通过数值法来求解[1]。Masory等[2]综合考虑杆长限制、驱动杆的尺寸干涉、转动副的转角限制,求解了并联机构的工作空间。陈小岗等[3]采用数值方法计算了6-UPS并联机床的工作空间并绘制了相应的位姿空间图谱。一些学者针对如何在并联机构整体尺寸有限的情况下获得更大的工作空间进行了结构尺寸参数优化研究[4-6]。传统方法推导的雅可比矩阵前3列为长度单位量,后3列为量纲一的量,导致雅可比矩阵呈非均匀性。为了解决这一问题,Gosselin[7]推导了一种新的雅可比矩阵,它是末端执行器上3点的速度向驱动杆速度的映射。Gosselin等[8]基于雅可比条件数提出了用全域灵巧度指数(global dexterity index,GDI)来衡量并联机床的整体运动学性能。
本文针对BJ-04-02(A)型交叉杆并联机床工作空间小、姿态实现能力有限等缺陷,采用三维搜索方法对其在杆长限制、杆件尺寸干涉及转动副转角限制约束条件下的工作空间进行求解,推导其操作度均匀的新型雅可比矩阵,分析机床各结构参数对工作空间和灵巧度的影响,以工作空间和灵巧度为优化目标,对该机床结构参数进行优化,为该类机床的结构改进提供理论依据。
1 交叉杆并联机床运动学反解
BJ-04-02(A)型交叉杆并联机床是Stewart并联机构的变异结构,如图1所示,定平台的6个铰链点Ai(i=1,2,…,6)的外接圆半径为Ra,弦A2A3、A4A5、A1A6所对应的圆心角为θ;动平台分上下两层,两层之间的距离为H,下层3个铰链点B1、B3、B5的外接圆半径为Rb,上层3个铰链点B2、B4、B6的外接圆半径为Rb/3;驱动杆的最小长度、最大长度分别为lmin、lmax;驱动杆的直径为D0。

(a)机床实物图(b)机床结构简图图1 BJ-04-02(A)型交叉杆并联机床
在机床静平台和动平台上分别建立静坐标系OXYZ和动坐标系oxyz,静坐标系的原点O位于静平台上各铰链点外接圆的圆心,Y轴为A1A2的中垂线,Z轴垂直于静平台向上,X轴由右手螺旋定则确定;动坐标系的原点o位于动平台下层各铰链点外接圆的圆心,y轴为B1B3的中垂线,z轴垂直于动平台向上,x轴由右手定则确定,如图1b所示。
当给定交叉杆并联机床结构尺寸Ra、θ、Rb、H后,由几何关系容易得到静平台和动平台上各铰链点在各自坐标系中的坐标向量Ai和bi。动平台上任一点在动坐标系oxyz中的向量bi可通过坐标变换方法变换到静坐标系中的向量Bi:
Bi=Tbi+P
(1)
其中,T为动平台姿态的方向余弦矩阵,P为动坐标系的原点在静坐标系中的坐标向量。由此可得到驱动杆在静坐标系中的杆长矢量li:
li=Bi-Ai=Tbi+P-Ai
(2)
从而得到位置反解计算方程:
(3)
2 交叉杆并联机床工作空间的求解
2.1约束条件
影响并联机床工作空间的因素有很多,其中杆长限制、驱动杆的尺寸干涉以及转动副转角的限制是最主要的3个因素[1]。
2.1.1杆长限制
交叉杆并联机床受其结构限制,其驱动杆杆长约束条件为
(4)
式中,lmin、lmax分别为各杆最小长度、最大长度。
2.1.2驱动杆的尺寸干涉
实际驱动杆是有一定几何尺寸的,仅依据运动学反解得到的工作空间内各杆是有可能发生干涉的。设相邻两驱动杆中心轴线的空间异面直线距离为Dj,k,则交叉杆并联机床驱动杆不发生干涉的条件为
Dj,k>D0
(5)
j=1,3,5;k=6,2,4或j=1,3,5;k=2,4,6
2.1.3转动副转角的限制
设交叉杆并联机床静平台和动平台与各驱动杆连接的虎克铰与球铰的最大转角分别为θAmax、θBmax,nAi、nBi分别表示与静平台第i个虎克铰的基座和与动平台第i个球铰的基座固结的坐标系Z轴方向的单位矢量,则转角约束条件为
(6)
2.2求解方法
本文用三维搜索的方法来求解交叉杆并联机床的工作空间,将三维空间微分成大小一样的正六面体(边长为e),判断并联机床动平台的参考点在每个正六面体中心处是否属于其定向工作空间。判断一个点是否属于其定向工作空间,取决于运动学逆解所得的机构位形是否满足2.1节中3个约束条件。
设单个正六面体的体积为ΔV,则整个工作空间的体积 (workspacevolume)Vws为
(7)
其中,w为满足约束条件的正六面体个数。工作空间的量纲一指数(workspacevolumeindex)Iwv定义为工作空间体积Vws与平台体积Vp的比值。即
Iwv=Vws/Vp
(8)
式中,Vp为包含机构及工作空间体积的圆柱体的体积。
3 基于新型雅可比矩阵的灵巧度计算
本文采用Gosselin[7]提出的末端执行器三点法来推导交叉杆并联机床量纲一致性的雅可比矩阵。在动平台下层面上定义3个线性无关的点T1(x1y1z1)、T2(x2y2z2)、T3(x3y3z3),动平台相对静平台的位姿就可以用点T1、T2、T3来表示。作直线QBj与T1T3平行且交T1T2于Q点,则Bj的绝对坐标就可用3个点T1、T2、T3表示,如图2所示。即
OBj=OQ+QBj=k1OT1+k2OT2+
k3(OT3-OT1)=kj,1OT1+kj,2OT2+kj,3OT3
(9)
其中,kj,1、kj,2、kj,3均为常数,与具体选定的3个点T1、T2、T3有关。
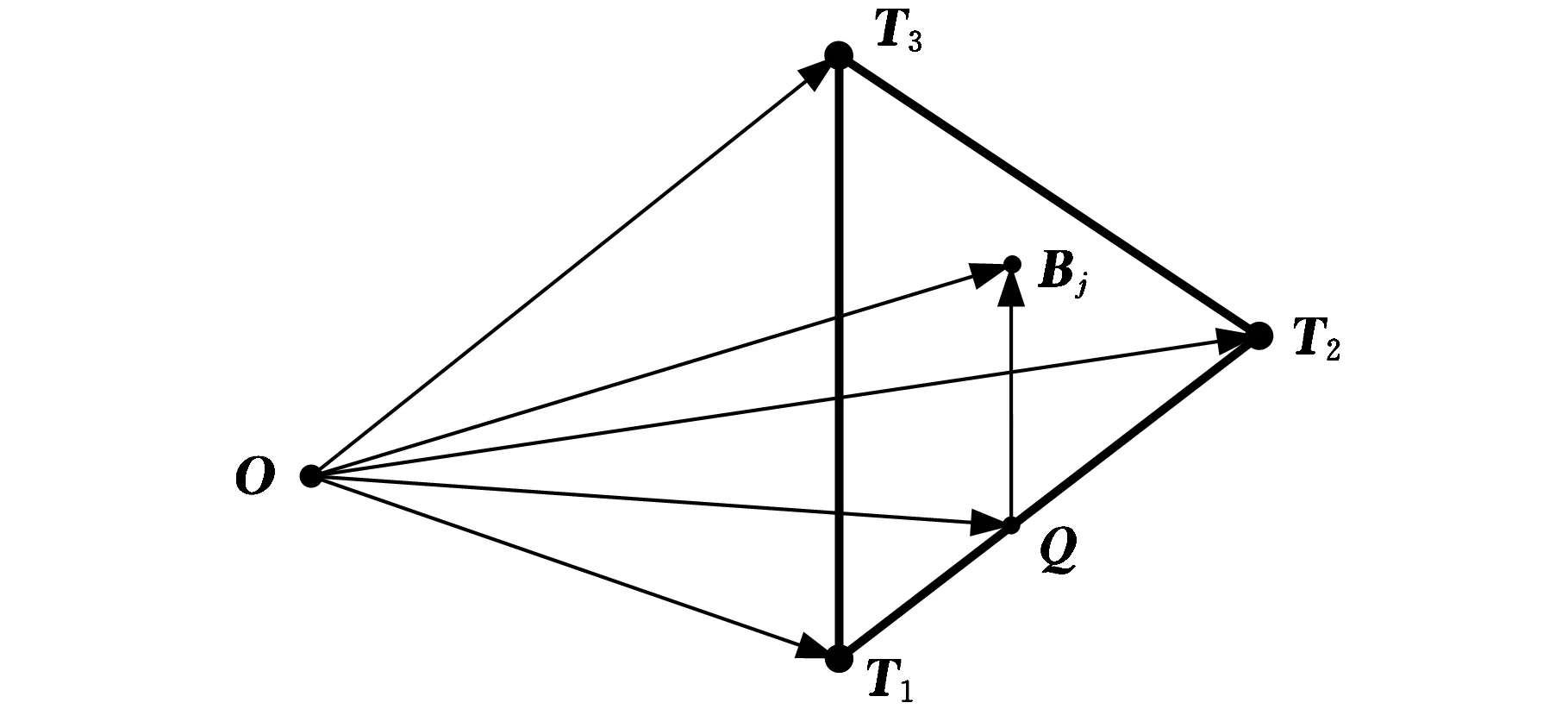
图2 动平台铰链点坐标的三点表示
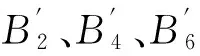
AjBj=ljuj=
(10)
其中,n0为动平台平面的单位法向量。对式(10)两边同时求导得
(11)
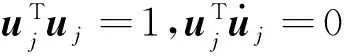
(12)
由几何关系可知,动平台任意时刻的平面法向量为
n=[n1n2n3]T=T1T2×T2T3=
(13)
设n=f1t1+f2t2+f3t3,则有
(14)
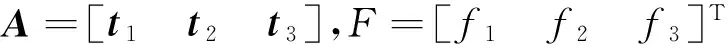
AF=n
(15)
联立式(13)~式(15)可以得到f1、f2、f3,因此有
(16)
理论上T1、T2、T3可以选取动平台上任意3个线性无关的点,为计算方便,选取动平台下层面的3个铰链点B1、B3、B5。将式(16)代入式(12)中得到的矩阵形式为
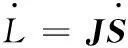
(17)
其中,J为新型雅可比矩阵,它是动平台速度向驱动关节速度的映射,具有可操作度均匀性的特点。
全域灵巧度性能度量指标IGD表示并联机床在其整个工作空间内或其工作空间的某个合理的中央部分灵巧度的平均值[8],即
(18)
其中,dW代表工作空间内某位置一个无限小的元素,k(J)是在指定工作点处雅可比矩阵的条件数。而雅可比矩阵的条件数又可定义为[9]
k(J)=‖J‖‖J-1‖
(19)
最终化简为
k(J)=σmax/σmin
(20)
其中,σmax为J的谱范数,其值为JTJ最大特征值的开方;1/σmin为J-1的谱范数,其值为JTJ最小特征值的开方。
4 交叉杆并联机床结构参数优化设计
(a)视角(-37.5 mm,30 mm)

(b)YZ向视图

(c)XZ向视图
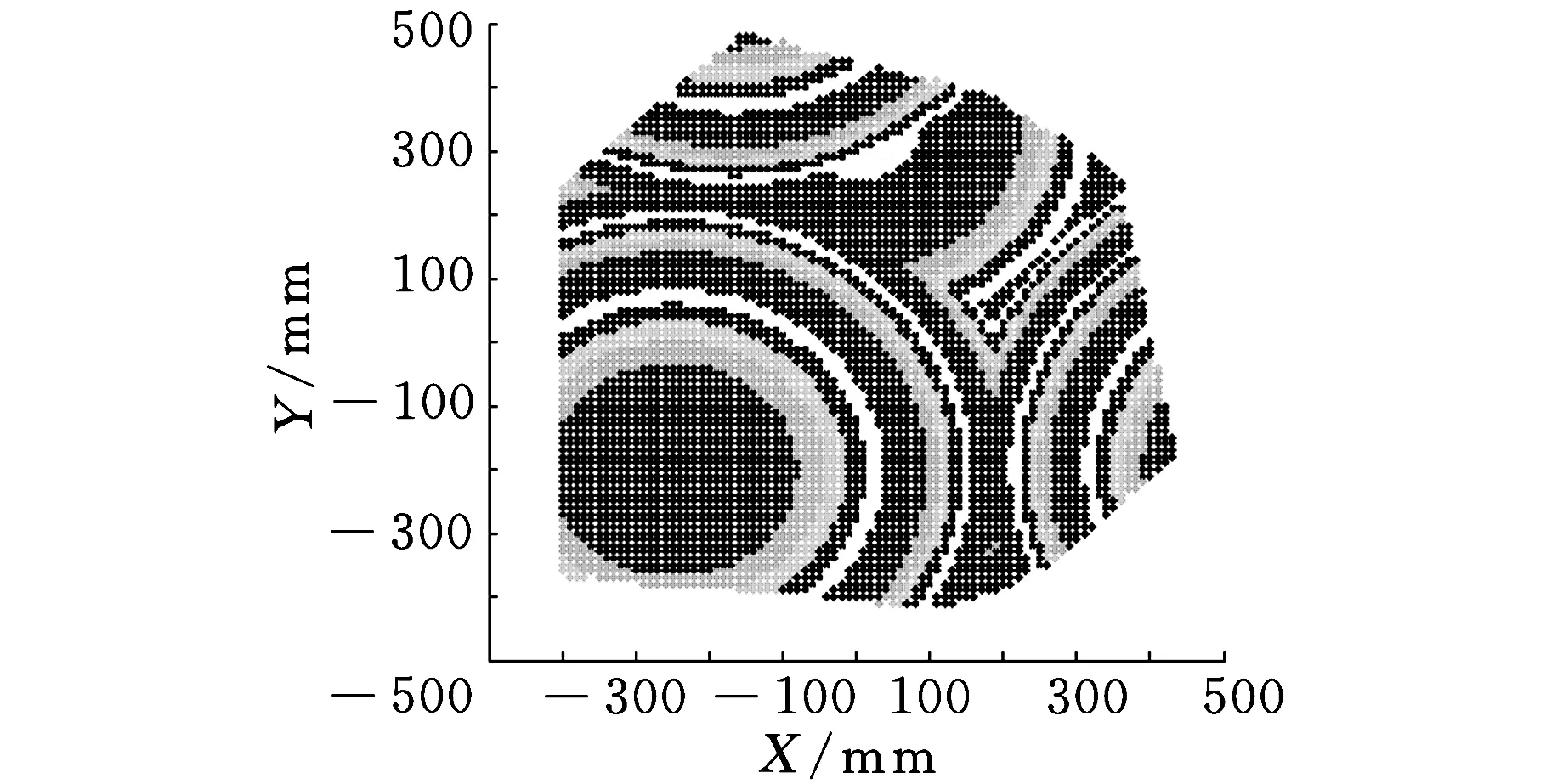
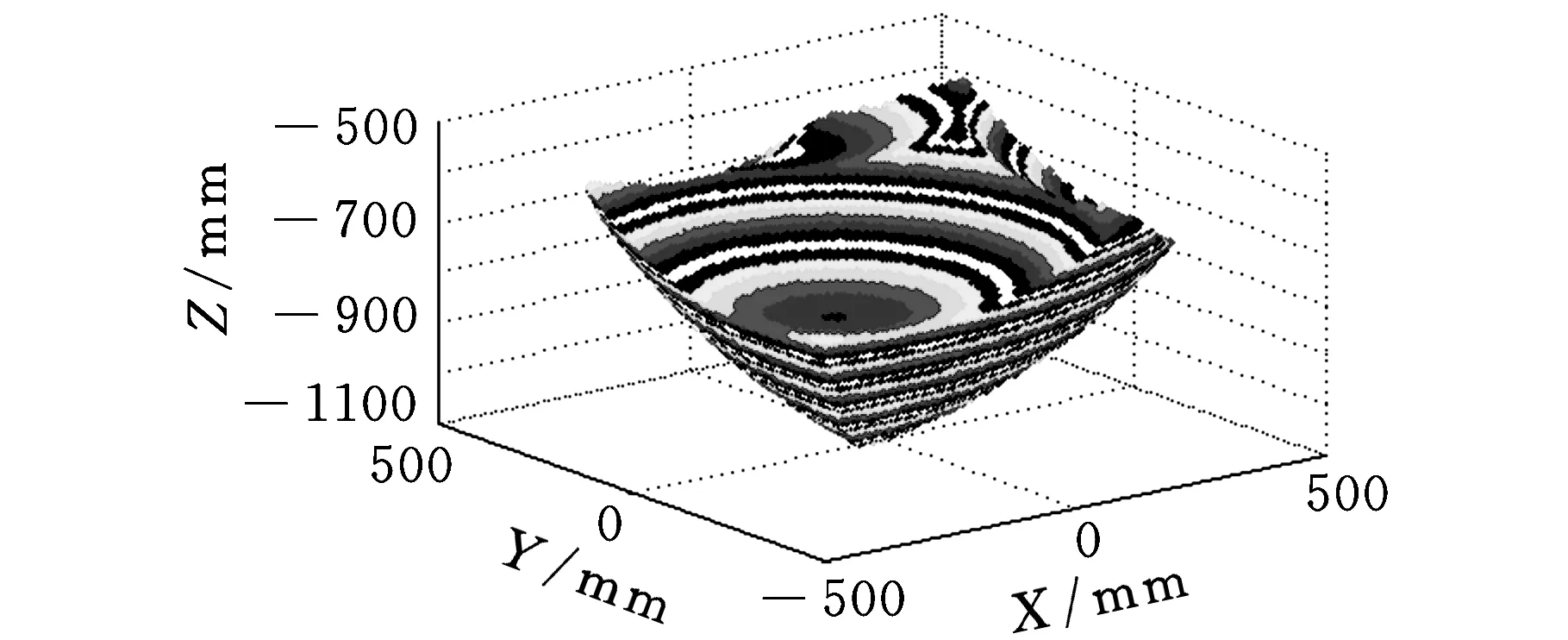
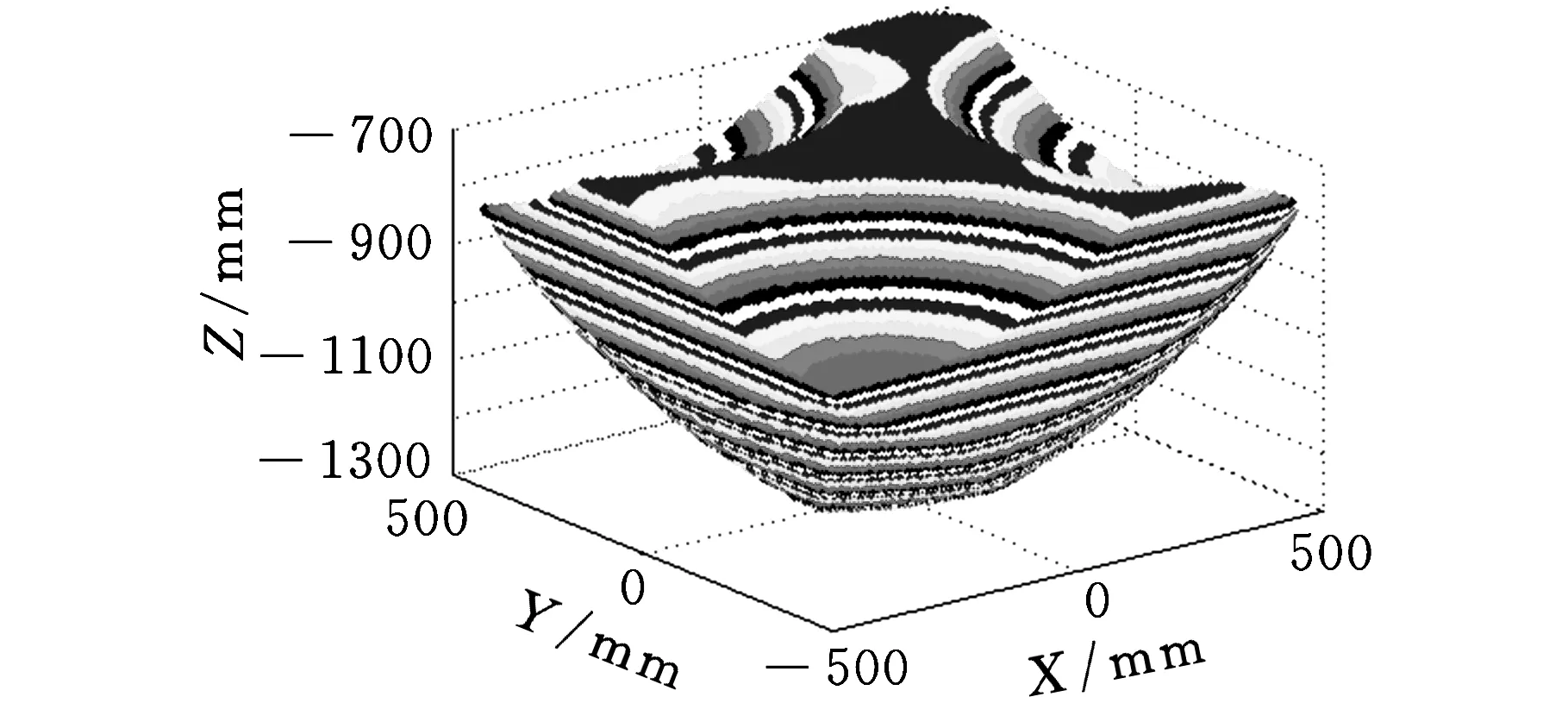
(d)XY向视图图3 交叉杆并联机床的工作空间
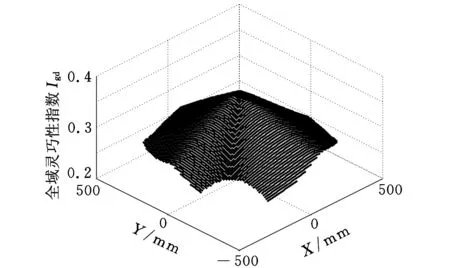
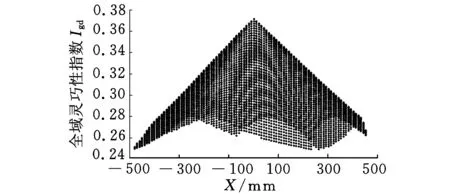
(a)视角(-45 mm,45 mm)

(b)YZ向视图
(c)XZ向视图
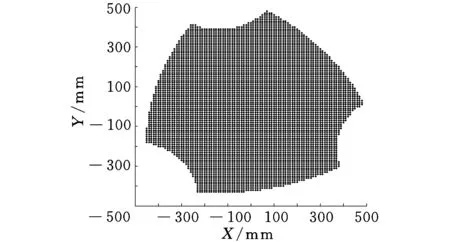
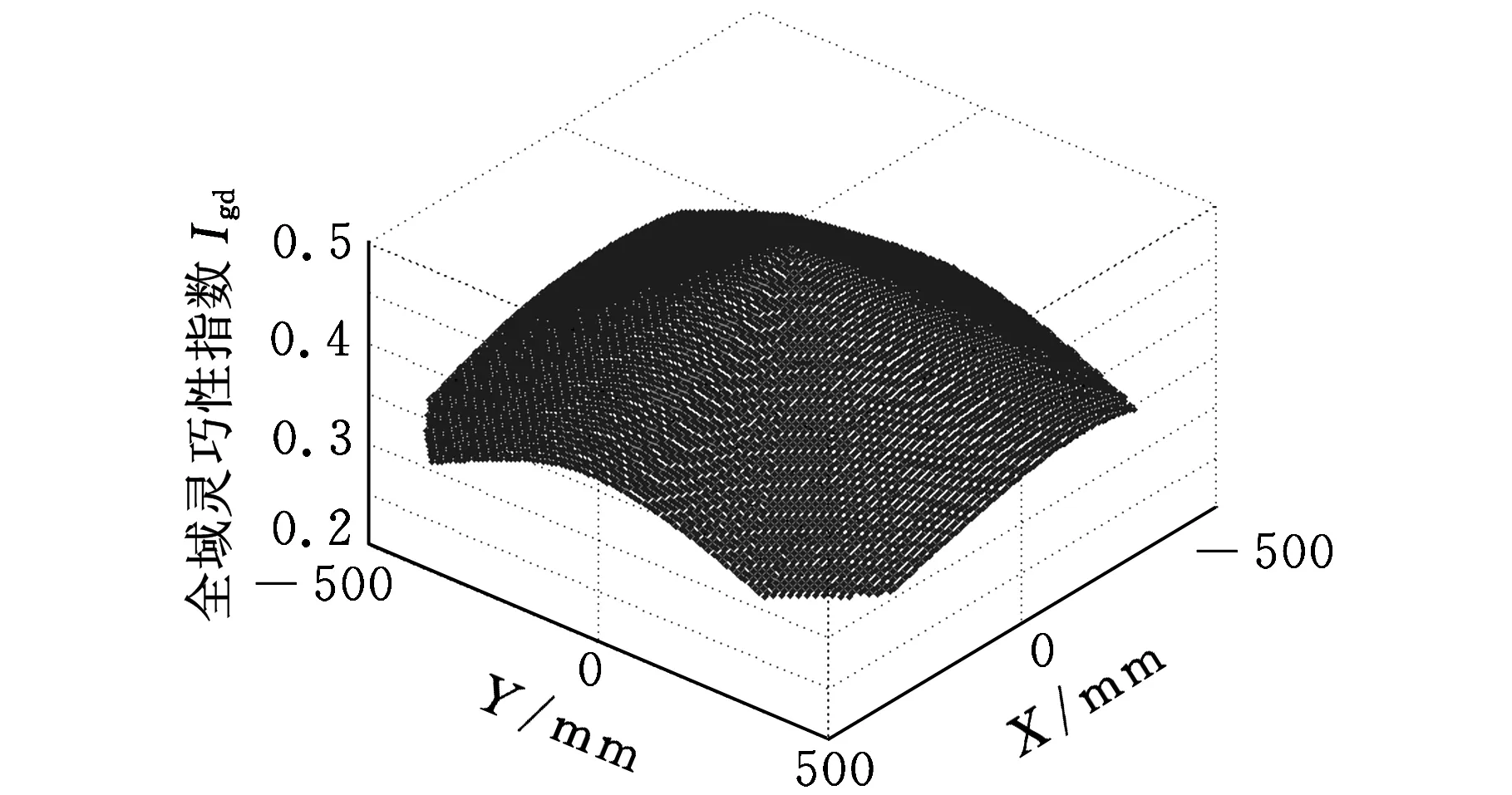
(d)XY向视图图4 交叉杆并联机床灵巧度分布
计算得到交叉杆并联机床随其各结构参数在一定范围内取离散值时工作空间的量纲一指数和全域灵巧度指数,如图5~图10所示。其中Rb、H、lmin、lmax-lmin均除以Ra,则横坐标变为量纲一的量。
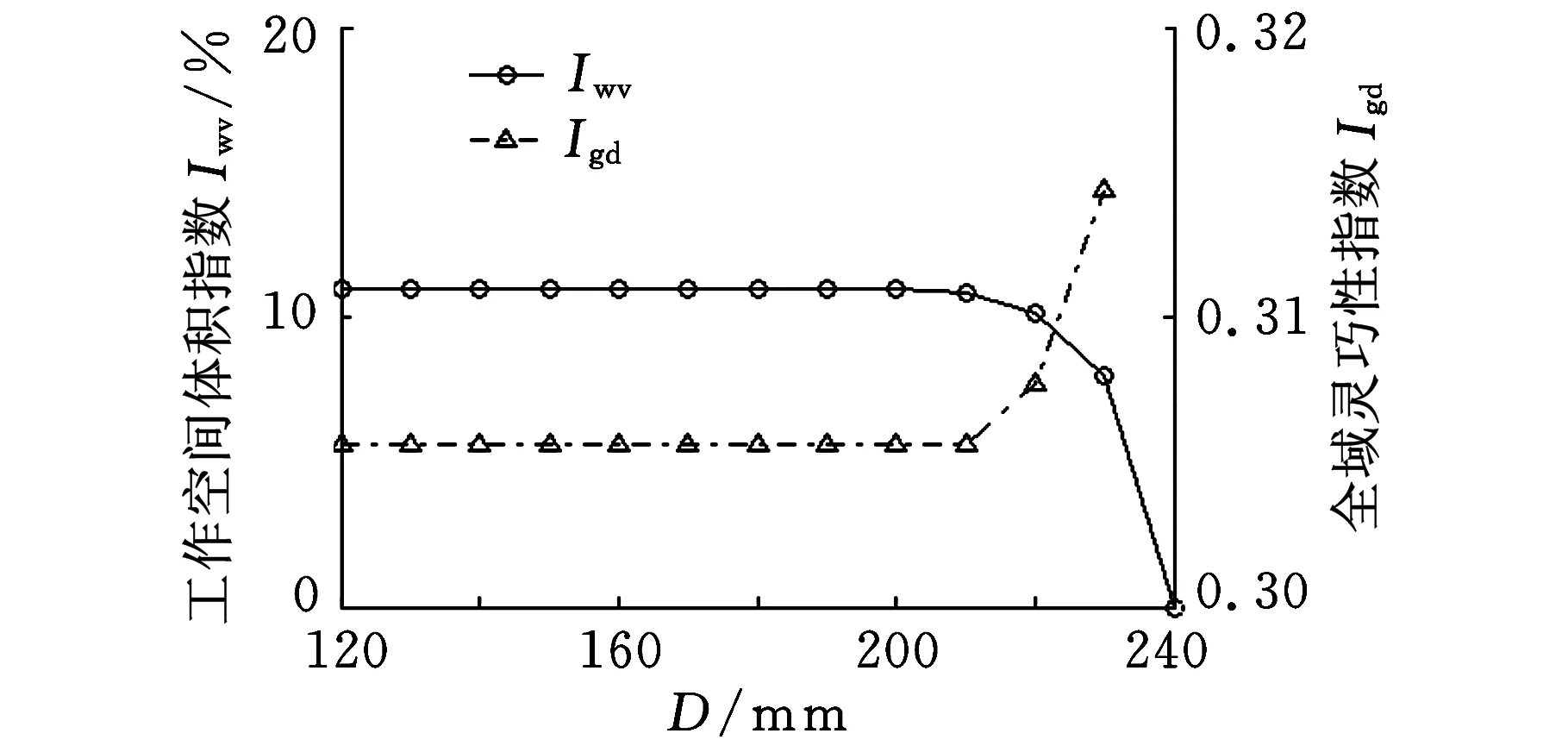
图5 Iwv和Igd随D变化曲线
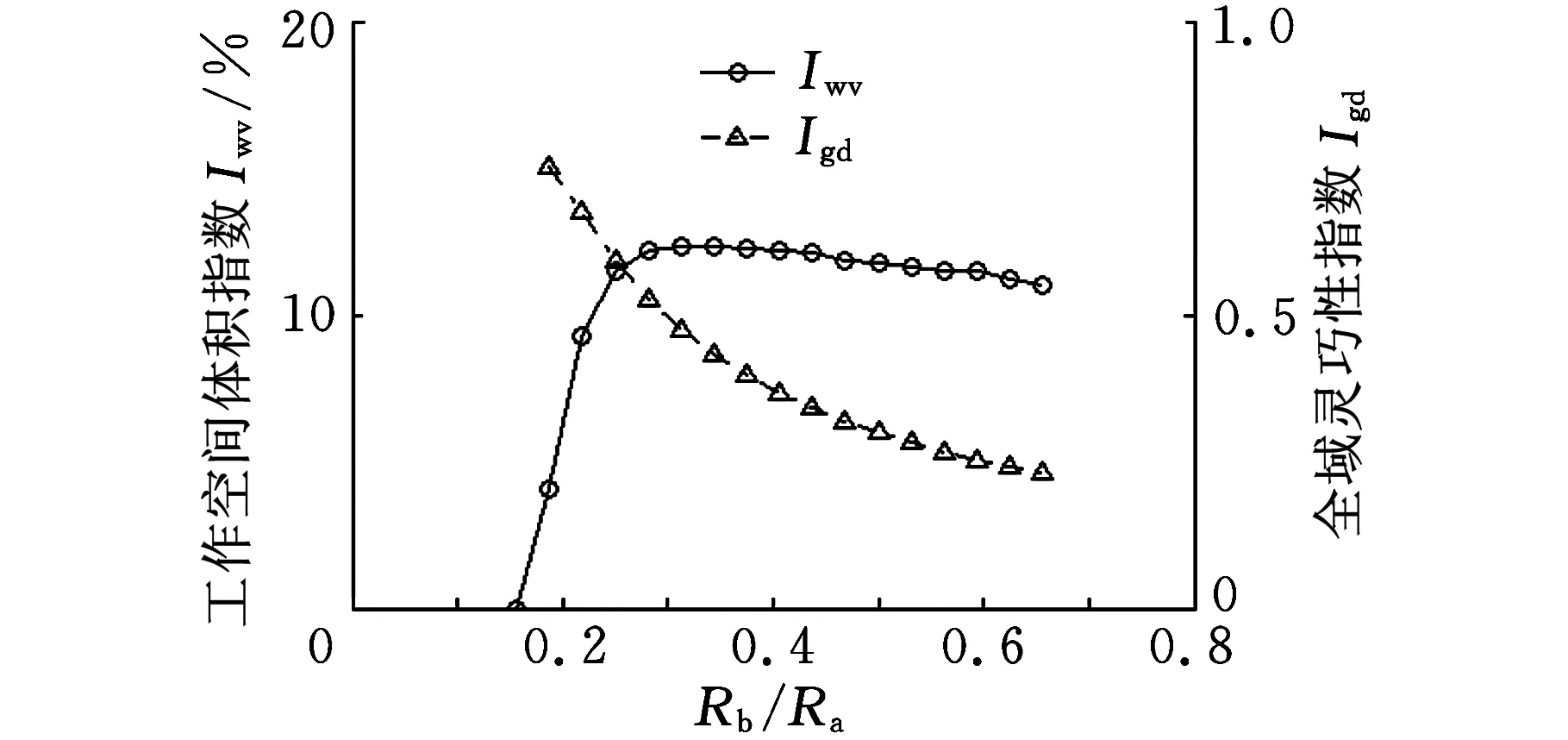
图6 Iwv和Igd随Rb/Ra变化曲线
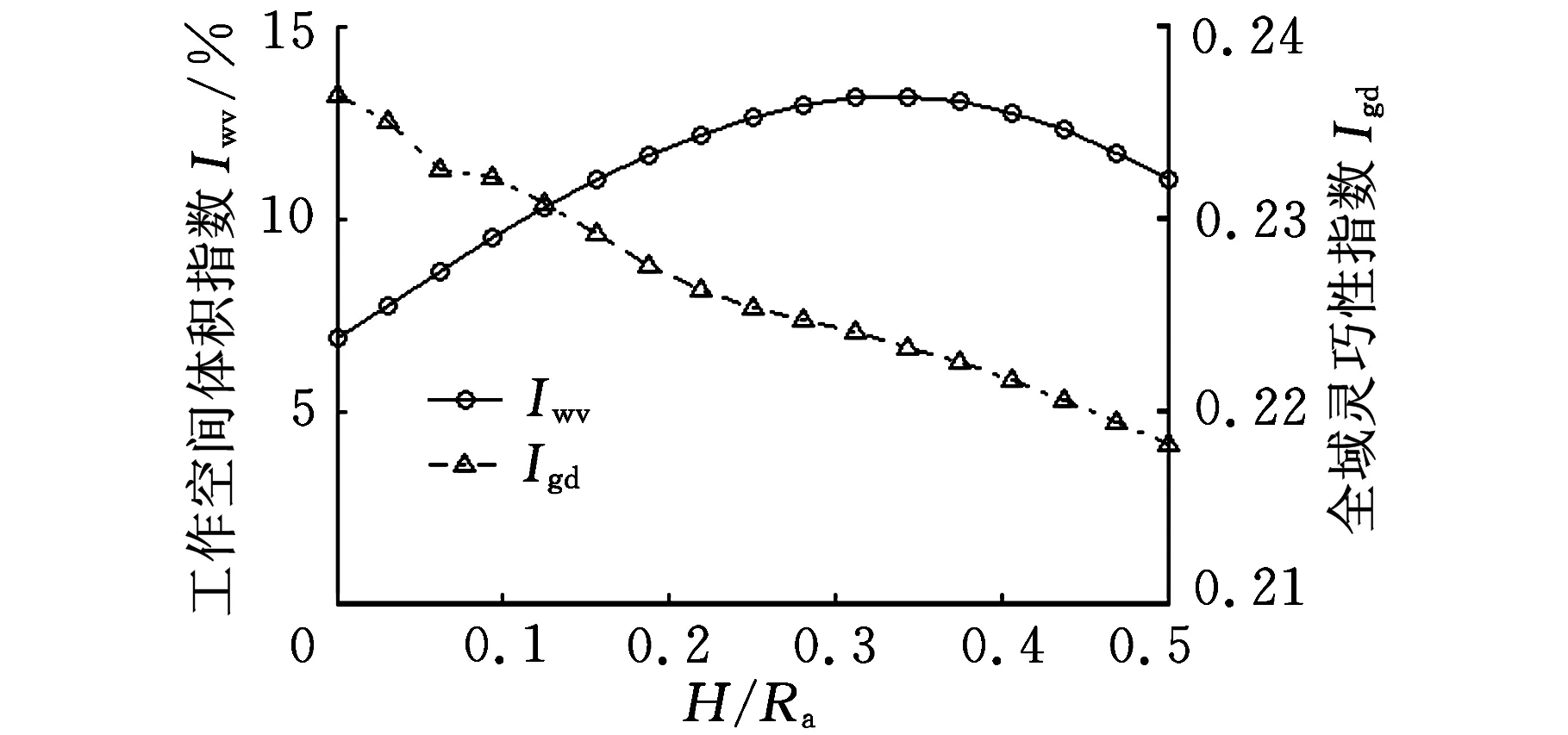
图7 Iwv和Igd随H/Ra
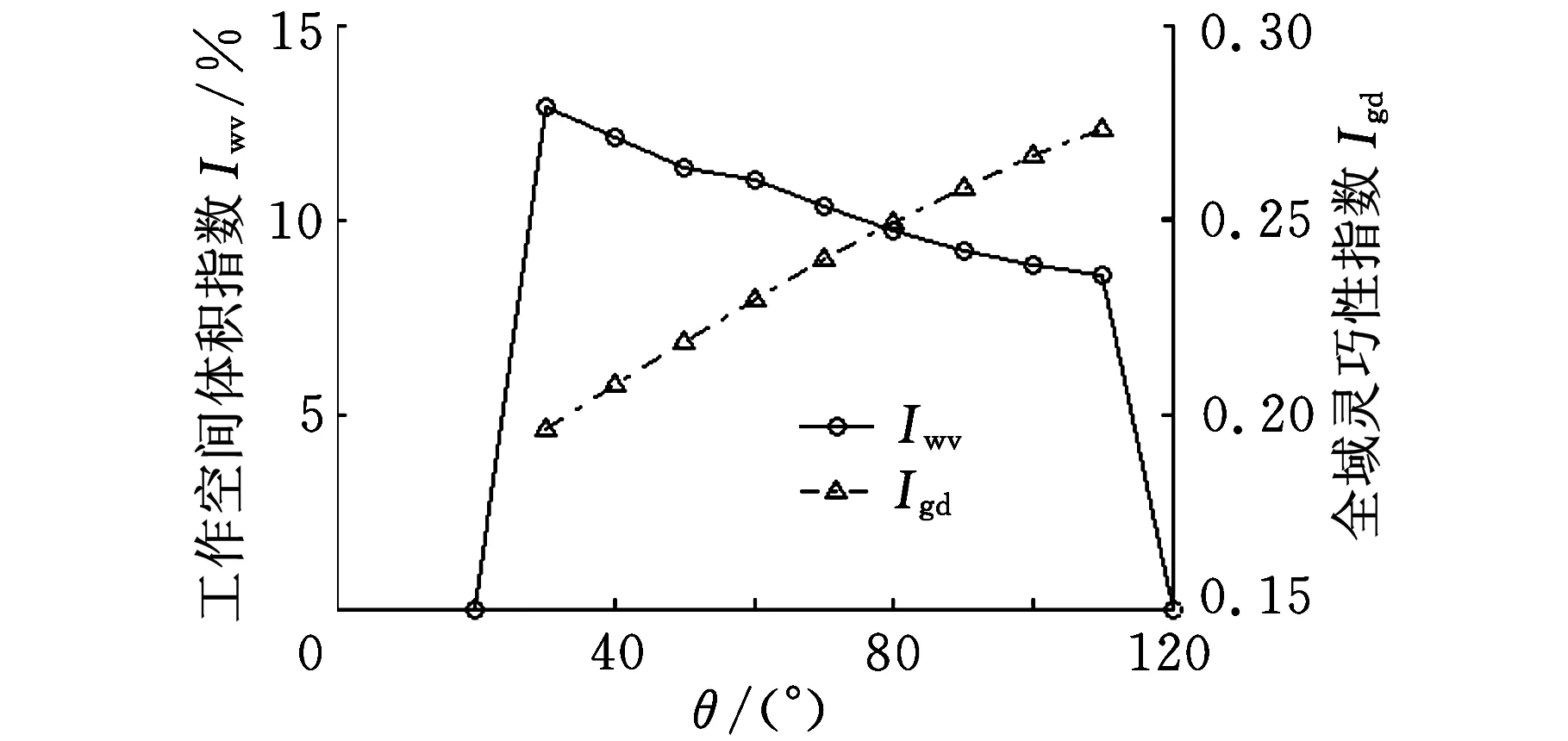
图8 Iwv和Igd随θ变化曲线
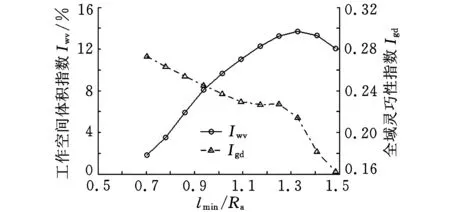
图9 Iwv和Igd随lmin/Ra变化曲线

图10 Iwv和Igd随(lmax-lmin)/Ra变化曲线
由图5~图10中的曲线变化可以得到如下规律:
(1)当驱动杆直径小于某个临界值时,动平台在整个工作空间运动时驱动杆都不会发生干涉;驱动杆直径不是并联机床灵巧度的影响因素,灵巧度变化是因为杆件尺寸干涉使工作空间减小。
(2)Iwv先随Rb/Ra的增大而增大,后随Rb/Ra的增大而缓慢减小,当Rb/Ra=0.34时,Iwv取得最大值;Igd随着Rb/Ra的增大而减小。
(3)Iwv先随H/Ra的增大而增大,后随H/Ra的增大而减小,当H/Ra=0.34时,Iwv取最大值;Igd与H/Ra成反比,但其变化幅度仅为0.02,因此H/Ra对Igd影响很小,可以忽略。
(4)当30°≤θ≤110°时,Iwv与θ成反比,但当θ<30°或θ>110°时,Iwv因驱动杆杆件尺寸干涉而严重减小;Igd与θ成正比。
(5)交叉杆并联机床驱动杆杆长自身约束条件为lmin>lmax-lmin,所以lmin/Ra>(lmax-lmin)/Ra=0.86,在此范围内,Iwv先随lmin/Ra的增大而增大,后随lmin/Ra的增大而减小,当lmin/Ra=1.33时,Iwv取得最大值;Igd与lmin/Ra成反比。
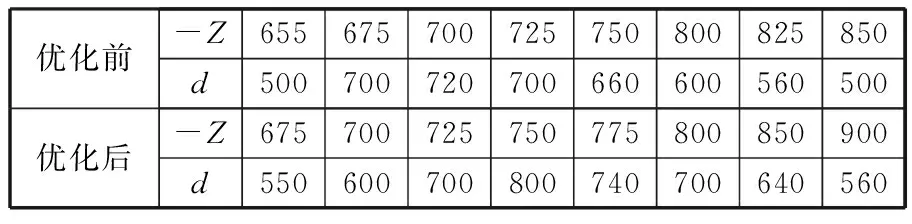
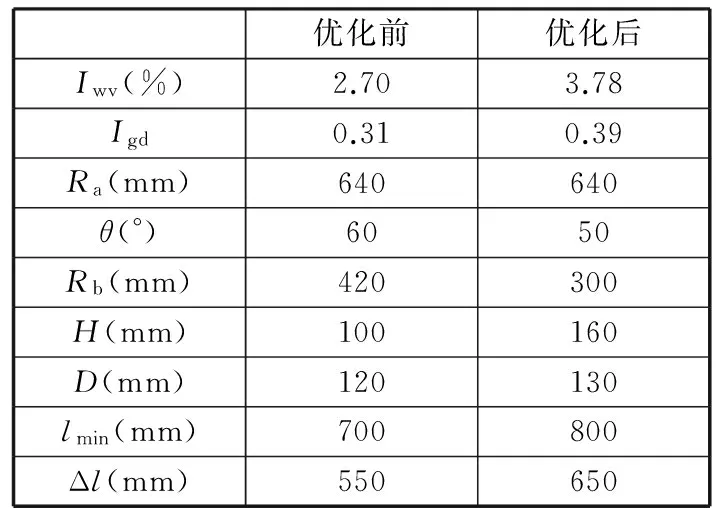
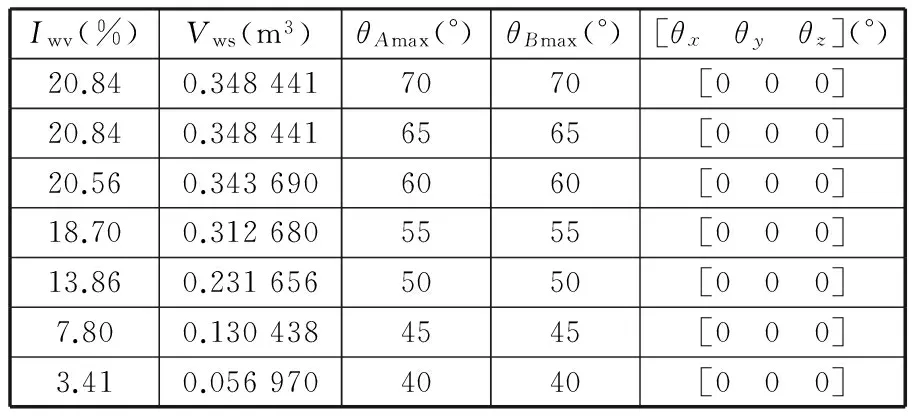
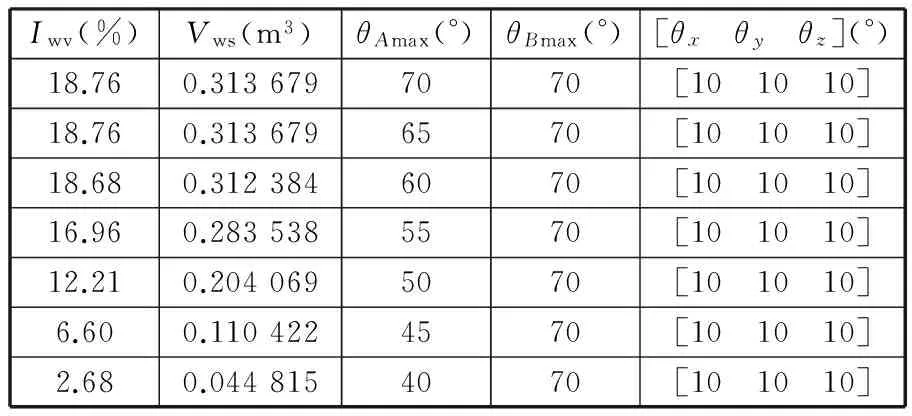
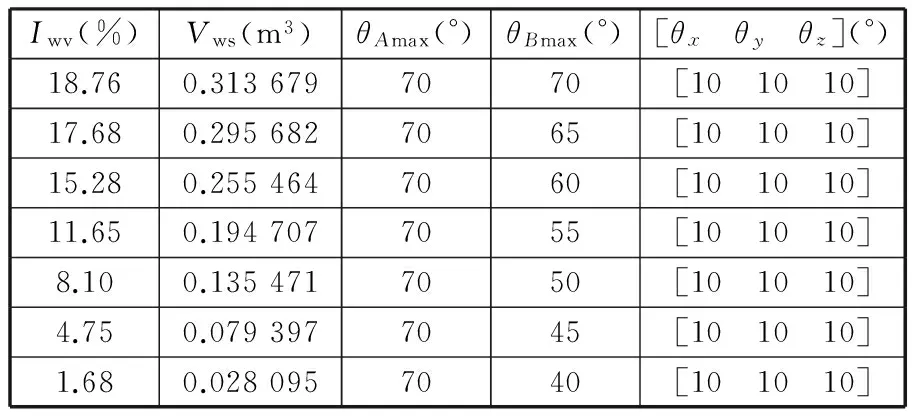
(6)在杆长自身约束条件(lmax-lmin)/Ra 图5~图10中的每条曲线都是通过连接相邻离散点得到的,并非真实的变量函数关系。为了揭示交叉杆并联机床的Iwv和Igd随其结构参数的具体变化关系,本文采用最小二乘法对图5~图10中交叉杆并联机床的Iwv和Igd关于其各结构参数的点列数据进行曲线拟合。 令x1=Rb,x2=H,x3=θ,x4=lmin,x5=lmax-lmin;f1(x)为机床工作空间关于机床各结构参数变量的函数;f2(x)为机床灵巧度关于机床各结构参数变量的函数。由此,得到交叉杆并联机床的Iwv和Igd关于其各结构参数变量的各具体函数f1(x1),f1(x2),…,f1(x5)和f2(x1),f2(x2),…,f2(x5)。 定义参数变量为 定义目标函数为 maxf1(X)=max(Iwv(X))= maxf2(X)=max(Igd(X))= 其中,约束条件为 利用Mathematica软件求解目标函数maxf1(X)和maxf2(X)的最大值,得到对应的参数变量:x11=370.107 mm,x12=210.939 mm,x13=30°,x14=850.704 mm,x15=768 mm和x21=96 mm,x22=2.64794×10-9mm,x23=110°,x24=550.4 mm,x25=384 mm。 由于工作空间对并联机床来说具有明确需求,而灵活度指标虽也重要,但其具体大小没有具体明确要求,即工作空间比灵活度相对于并联机床的权重较大。针对工作空间和灵巧度相对于并联机床的重要程度不同,采用加权系数法将机床多目标优化问题转化为单变量问题。即 xn=(k1x1n+k2x2n)/(k1+k2)n=1,2,…,5 其中,k1、k2分别为x1n、x2n的权重,且k1+k2=1。选取k1=0.5,0.6,…,0.9且k2=0.5,0.4,…,0.1这5种情况,得到对应的机床结构参数变量优化值,见表1。 表1 加权系数法得到的5组机床结构参数优化值 结合图5~图9中的曲线变化规律与表1的数据,在确保机床能够获得较大工作空间的同时兼顾机床灵巧度的情况下,并且考虑杆件尺寸干涉和机床刚度以及主轴安装等因素,最终选取D=130 mm、Rb=300 mm,H=160 mm,θ=50°,lmin=800 mm,lmax-lmin=650 mm,对该机床进行优化设计,得到参数优化后的工作空间和灵巧度分布,分别如图11和图12所示。 图11 交叉杆并联机床优化后的工作空间 图12 交叉杆并联机床优化后的灵巧度 为了适应多坐标数控加工的需要,将灵巧度工作空间的规则内接几何形体定义为机床的编程工作空间。对于Z取不同的值,工作空间截面图是不同的。表2给出了该机床优化前后部分工作空间截面所包含最大圆的直径尺寸d。 表2 交叉杆并联机床工作空间截面尺寸 mm 由表2可以发现,该机床优化前在Z=-700 mm时的工作空间截面最大,其Z向主要加工区域为-850 mm≤Z≤-655 mm,工作空间可包含直径为500 mm、高度为195 mm的圆柱体;优化后在Z=-750 mm时的工作空间截面最大,Z向主要加工区域为-900 mm≤Z≤-675 mm,工作空间可包含直径为550 mm、高度为225 mm的圆柱体。 表3给出了交叉杆并联机床优化前后的Iwv、Igd及其尺寸参数,工作空间增加了0.4倍,全域灵巧度指数提高了0.26倍,达到了预期目标。由于本文中Igd是以新型雅可比矩阵为基础得到的,不会随机床结构参数同级放大或缩小而改变,故优化得到的机床尺寸参数可根据需要按比例缩放。 表3 交叉杆并联机床优化前后的Iwv和Igd及其尺寸参数 以上分析都是在假定θAmax=θBmax=75°时得到的,下面通过改变虎克铰和球铰最大转角来分析转动副转角对工作空间的影响。表4给出了该机床结构参数取以上优化值且动平台姿态欧拉角为[0 0 0]时虎克铰和球铰最大转角取不同值的工作空间。表5和表6分别给出了该机床结构参数取以上优化值且动平台姿态欧拉角为[10° 10° 10°]时虎克铰和球铰最大转角取不同值的工作空间。这里工作空间是指满足3个约束条件的所有位姿点的总和,而实际能得到的规则内接几何形体要小得多。 表4 工作空间随虎克铰和球铰最大转角的变化 表5 工作空间随虎克铰最大转角的变化 表6 工作空间随球铰最大转角的变化 由表4~表6可以发现:当动平台只做平移运动,虎克铰和球铰最大转角均大于65°时,工作空间不会受转动副转角限制而减小;当动平台既平移又转动时,球铰转角范围比虎克铰转角范围对工作空间的影响要大;如果动平台姿态变化,则工作空间也将随之改变,且动平台姿态角越大,其工作空间就越小。有效增加虎克铰和球铰转角范围对于扩大并联机床工作空间能起到关键作用。 (1)本文求解了BJ-04-02(A)型交叉杆并联机床在约束条件下的工作空间并探究了有效增加关节转动副转角范围和适当改变驱动杆长度对扩大并联机床工作空间起到的关键作用,而杆件尺寸干涉的可能性很小。 (2)采用自然坐标法推导了交叉杆并联机床量纲一致性的新型雅可比矩阵,并得到了该机床工作空间内的全域灵巧度指数分布。 (3)研究了交叉杆并联机床的各机构参数对其工作空间和灵巧度的影响规律。以增大机床工作空间和提高机床灵巧度为目标,对机床结构参数进行了优化设计并给出了该机床优化前后的工作空间所包含的最大圆柱体大小。 [1]黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006. [2]MasoryO,WangJ.WorkspaceEvaluationofStewartPlatforms[J].AdvancedRobotics,1995,9(4):443-461. [3]陈小岗,孙宇,刘远伟,等.6-UPS并联机床位姿空间图谱[J].中国机械工程,2013,24(10):1331-1335. ChenXiaogang,SunYu,LiuYuanwei,etal.PositionandOrientationWorkspaceAtlasofa6-UPSParallelMachineTool[J].ChinaMechanicalEngineering,2013,24(10):1331-1335. [4]MonsarratB,GosselinCM.WorkspaceAnalysisandOptimalDesignofa3-leg6-DOFParallelPlatformMechanism[J].IEEETransactionsonRoboticsandAutomation,2003,19(6):954-966. [5]杨晓钧,王知行,钟诗胜.基于工作空间和灵活性的并联机床结构参数优化设计[J].机械与电子,2004(2):14-17. YangXiaojun,WangZhixing,ZhongShisheng.ParameterOptimalDesignoftheParallelMachineToolforWorkspaceandDexterity[J].Machinery&Electronics,2004(2):14-17. [6]曹永刚,张玉茹,马运忠.6-RSS型并联机构的工作空间分析与参数优化[J].机械工程学报,2008,44(1):19-24. CaoYonggang,ZhangYuru,MaYunzhong.WorkspaceAnalysisandParameterOptimizationof6-RSSParallelMechanism[J].ChineseJournalofMechanicalEngineering, 2008,44(1):19-24.[7]GosselinC.DexterityIndicesforPlanarandSpatialRoboticManipulators[C]//Proc.IEEEInt.Conf.RoboticsandAutomation.Cincinnati,1990:650-655.[8]GosselinC,AngelesJ.AGlobalPerformanceIndexfortheKinematicOptimizationofRoboticManipulators[J].ASMEJournalofMechanicalDesign,1991,113(3):220-226. [9]于靖军,刘辛军,丁希伦,等.机器人机构学的数学基础[M].北京:机械工业出版社,2008. (编辑陈勇) Structural Parameter Optimization of a Crossbar Parallel Machine Tool Fang Xifeng1Zhang Sichong1Xu Qinhuan1Wang Tongyue2Liu Yuanwei2Chen Xiaogang2 1.Jiangsu University of Science and Technology,Zhenjiang,Jiangsu,212003 2.Huaiyin Institute of Technology,Huaian,Jiangsu,223001 Increasing workspace and improving dexterity are important taskes for the design of parallel machine tool. On the basis of inverse kinematics, workspace of the crossbar parallel machine tool with constraints was obtained via three-dimensional search method. New Jacobian matrix of the machine was also deduced by using the natural coordinate method. Dexterity distribution of the machine was acquired as well based on the workspace and new Jacobian matrix. Then, the impacts of structural parameters on workspace and global dexterity index were analyzed, then least square method was applied to curve fitting and the optimization of these structural parameters were carried out by introducing workspace value index and global dexterity index as the global optimization goals. Compared with the original data, each of them increases by 0.40 and 0.26 times respectively, achieving the aim of mechanism optimization. crossbar parallel machine tool;workspace;new Jacobian matrix;global dexterity index;structural parameter optimization 2013-08-28 江苏省高校自然科学基金资助项目(09KJB460003);江苏省数字化制造技术重点实验室开放基金资助项目(HGDML-1102);江苏省船舶先进设计制造技术重点实验室开放基金资助项目(CJ1201) TH112;TH122< class="emphasis_italic">DOI :10.3969/j.issn.1004-132X.2015.01.007 方喜峰,男,1971年生。江苏科技大学机械工程学院教授、博士(后)。主要研究方向为智能设计与制造、数控加工技术等。发表论文40余篇,获省级科技进步奖3项。张思崇,男,1990年生。江苏科技大学机械工程学院硕士研究生。许钦桓,男,1990年生。江苏科技大学机械工程学院硕士研究生。汪通悦,男,1969年生。淮阴工学院江苏省数字化制造技术重点实验室教授、博士。刘远伟,男,1954年生。淮阴工学院江苏省数字化制造技术重点实验室教授。陈小岗,男,1981年生。淮阴工学院江苏省数字化制造技术重点实验室讲师、博士研究生。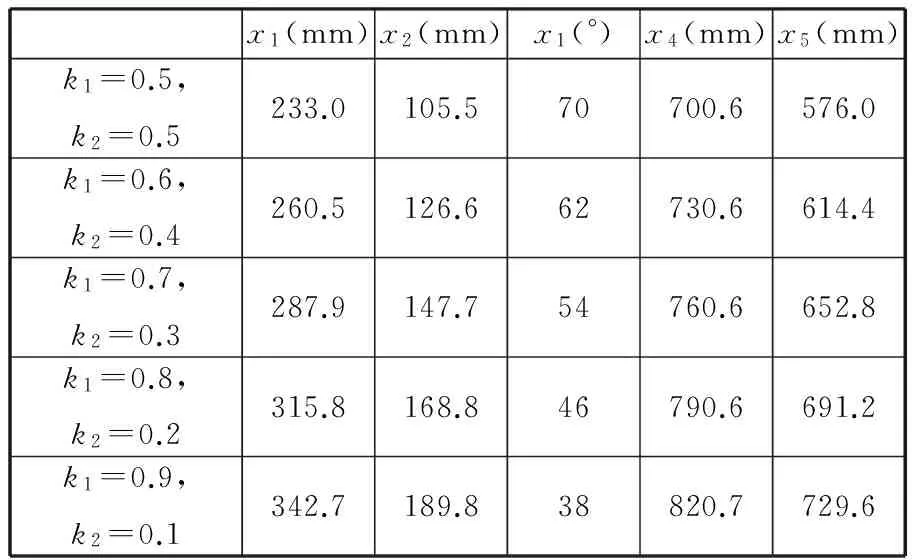
5 结论

