多杆高速机械压力机机构优化设计

李烨健　孙　宇　胡峰峰

南京理工大学，南京，210094

多杆高速机械压力机机构优化设计

李烨健孙宇胡峰峰

南京理工大学，南京，210094

为了有效发挥压力机的性能、解决机械压力机高速化带来的一系列问题，建立了一种以曲柄最短、冲压转角最大为评价指标的多杆高速机械压力机主传动机构几何参数综合优化数学模型，并利用MATLAB构建了该机构的优化模型。优化结果表明：该机构的冲压转角增大了13.5%，主滑块加速度减小了35.3%，在下死点附近，位移曲线较平滑，有利于冲裁过程中材料的充分变形和动平衡的设计，且有助于提高下死点的动态精度。

高速压力机；多杆机构；优化设计；运动轨迹

0　引言

近年来，随着电子、通信及汽车工业的迅猛发展，市场对冲压零件的需求量迅速增大，为了满足市场对冲压零件的需求，世界各国都在不断地提高压力机的速度[1-3]。然而，如何解决高速化给机构几何参数优化带来的一系列问题，充分发挥压力机的工作性能，使其高效地工作已成为人们非常关注并重点研究的课题。目前，国外对高速压力机传动机构的研究相对较成熟，如瑞士的Bruderer公司、美国的Minster公司都进行了深入研究并开发出相关产品[4-5]。近年来，国内有学者以下死点附近的滑块速度及其波动、曲柄驱动扭矩、速度和加速度误差、机构高度以及机构压力角或传动角等为评价指标，利用GA、SQP、SLP等算法以及步长搜索法对压力机八杆内滑块机构进行了优化，利用ANSYS、ADAMS的Insight功能模块对主传动系统各杆件几何参数进行优化，提高了设计的效率[6-9]。上述研究的研究对象均为低速压力机传动机构，几何参数优化的评价指标不一定适用于对高速压力机机构几何参数的评价。对于几何参数常规设计方法，首先给定机构的某些参数，然后利用作图法或解析法不断修改设计参数，直至得出满意的曲柄长度和连杆长度，重复工作量大，精度不高，设计的结果是唯一的，但不一定是最佳的。机构的运动规律与连杆机构的几何参数之间存在错综复杂的非线性关系，寻找一组满足各约束的机构几何参数有一定的困难[10]。目前，高速压力机的多杆主传动机构仍较复杂，存在构型种类繁多、设计理论不够完善和性能低等亟需解决的问题。因此，寻找合适的机构优化评价指标已成为高速压力机机构优化设计的关键问题。

为了提高压力机的工作性能，得到最优的工作曲线，降低后续设计的难度，本文根据多杆高速机械压力机的性能要求，以曲柄最短和冲压转角最大为评价指标，对研发中的多杆高速机械压力机机构几何参数进行优化设计。

1　机构模型的建立

多杆高速压力机传动机构原理示意图见图1。该机构主要由机架、对心曲柄滑块机构、拉杆、上下肘杆和主滑块组成。曲柄匀速圆周转动，通过连杆带动副滑块沿导轨在竖直方向运动，副滑块的竖直运动使拉杆上下摆动，从而使肘杆左右摆动，实现主滑块沿导轨的直线往复运动。在该机构中，肘杆可以放大驱动力，同时肘杆吸收了压力机工作时的大部分冲压载荷，避免电机直接受到工作载荷的冲击，使其运行平稳。

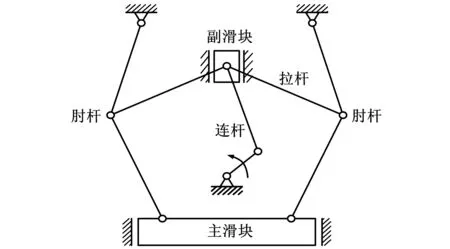
图1　多杆高速压力机原理示意图

2　多杆压力机的优化设计

一般的优化问题是在d维欧氏空间中寻找一个点x=(x1,x2,…,xd)T，在满足gi(x)≤0和hj(x)=0约束条件时，使f(x)取最小值。上述优化问题可简写为

式中，f(x)、gi(x)、hi(x)为d元函数；f(x)为目标函数；gi(x)为不等式约束条件；hi(x)为等式约束条件；x为设计变量。

2.1设计变量

为表述方便，建立图2所示的单边传动机构及坐标系，坐标原点位于曲柄的旋转中心O0，x轴正向为水平向右，y轴正向为垂直向上。图2中，m为上肘杆与机身上铰点水平距离；h为上肘杆与机身上铰点垂直距离；n为主滑块宽度尺寸。

图2　单边传动机构

对图2进行运动分析可知，决定该多杆机构运动规律的几何参数有曲柄长度l1，连杆长度l2，拉杆长度l3，上下肘杆长度l4、l5，主滑块铰点位置参数n和上铰点位置参数m、h。因此，该多杆压力机传动机构的独立设计参数共8个，故设计变量定义为

X=(x1,x2,x3,x4,x5,x6,x7,x8)T=

(l1,l2,l3,l4,l5,m,n,h)T

2.2目标函数

高速压力机主要用于落料和冲孔，工作在使工件产生弹性变形、塑性变形和断裂分离3个阶段，并且工作速度较高，冲裁时间较短，主滑块的工作特性对零件精度的影响至关重要。

为了使压力机得到较理想的运动规律输出，满足冲压工艺的要求，在给定设计要求的前提下，应合理确定压力机传动机构的评价指标。为提高经济性以及机床工作性能，本文提出了各杆长之和应最小、有较长的冲压时间、各杆件受力状况合理、主滑块速度波动及加速度应尽量小等设计要求。一般地，低速拉伸压力机只工作在使工件产生弹塑性变形阶段，对主滑块的工作速度和速度波动有一定限制，防止工件产生裂纹，以提高产品质量。

曲轴是机构的原动部分，其运行精度对下死点的运行精度有直接影响，对于高速压力机，热变形是无法忽略的。曲轴部位是整机的主要发热源，极易产生热变形，曲柄受力是影响发热的主要因素。曲柄长度与曲柄受力成正比，因此，应优化曲柄长度，以限制曲轴受力，从而减少曲轴发热，减小原动件的热变形，提高主滑块运行精度；同时也有助于减小驱动电机负载和转速波动，降低机构动平衡的设计难度，提高系统的可靠性和产品质量。

由压力机的实际工况和对机构的运动学分析可知，增大冲压转角，从而延长工件在冲压过程中的变形时间，使工件变形充分，机构的受力更加均匀，减小冲击，有助于提高机构的鲁棒性和产品的质量[11]。

机构的评价指标直接指引优化算法的搜索方向，所以在建立机构的评价指标时，合理确定优化目标函数非常重要。在机构的建模中，有学者直接以滑块速度最小、滑块速度波动最小、各杆长之和最小等为优化目标，利用加权系数法将它们组合成一个多目标函数。此时，滑块的速度波动、速度和杆的长度量纲是不一致的，而且它们的数量级相差也较大，在优化求解过程中，数量级大的优化目标分量会过于“强势”，极易出现“大数吃小数”的现象，最终难以得到满意结果。为了解决上述问题，本文对各个优化目标分量进行归一化处理，然后累加作为综合优化目标函数，解决了量纲不一致和数量级相差较大的问题。

某些优化目标在优化求解过程中，优化算法会干扰优化的搜索方向，会一味地沿着减小优化目标值的方向搜索，破坏机械压力机的传动角、相对位置等设计要求，难以得到良好的机械压力机设计方案。本文将这些优化目标转换为相应的约束函数来处理，减小其对总体性能的影响，保证压力机具有良好的综合性能。

综上所述，本文以减小曲轴受力、增大冲压转角作为优化目标，多杆压力机主转动机构的综合优化目标函数为

f(X)=l1/lc+φc/(φe-φs)

(1)

其中，lc为曲柄的优化目标长度，取20 mm；φe、φs分别为公称力行程结束和开始时对应的曲柄转角；φc是冲压转角的优化目标值，取0.5π。

2.3约束条件

对于给定的一种多杆高速压力机原理机构形式，与其匹配的机构参数有很多，但不是所有与其匹配的参数都能够作为压力机传动机构的工程化参数，需要综合考虑机构运动干涉、滑块行程、各杆件长度、机构高度及传动角等性能指标，同时结合机构成立的约束条件，建立机构工程化设计的约束条件[12-15]。约束条件如下。

(1)由于机身结构尺寸和装配需要的限制，需要对各构件长度和相对位置参数进行约束，不等式约束条件为

(2)

(2)为保证机构能正常运转以及装配和受力的需要，建立曲柄存在条件：

g3(X)=l1-l2+l≤0

(3)

式中，l为保证装配和受力需要选定的许用值，本文取260 mm。

(3)为保证整机的稳定性，需限制上梁的高度，则位置参数h的约束条件为

g4(X)=h-hmax≤0

(4)

式中，hmax为允许的上铰点最大高度。

(4)为保证主副滑块能正常运动，滑块可动的约束条件为

(5)

g6(X)=xO3-n-l5≤0

(6)

式中，xO3为O3点x坐标。

(5)为改善传动机构的受力状况，保证机构的正常运转和传力特性，减小工作过程中主轴和曲柄的受力，需使各点满足压力角的约束条件：

g7(X)=φ-φmax≤0

(7)

式中，φmax为允许的最大压力角，一般取40°～45°。

(6)为保证原理机构能实现预定的功能以及设计的合理性，当主滑块处于上死点位置时，拉杆不能处于水平姿态。

参照图2可得，当主滑块处于上死点位置时，拉杆与水平方向的夹角最小。此时，O2点坐标为(0,l2-l1)，图3中A点坐标为(0,h)，O4点坐标为(m,h)。

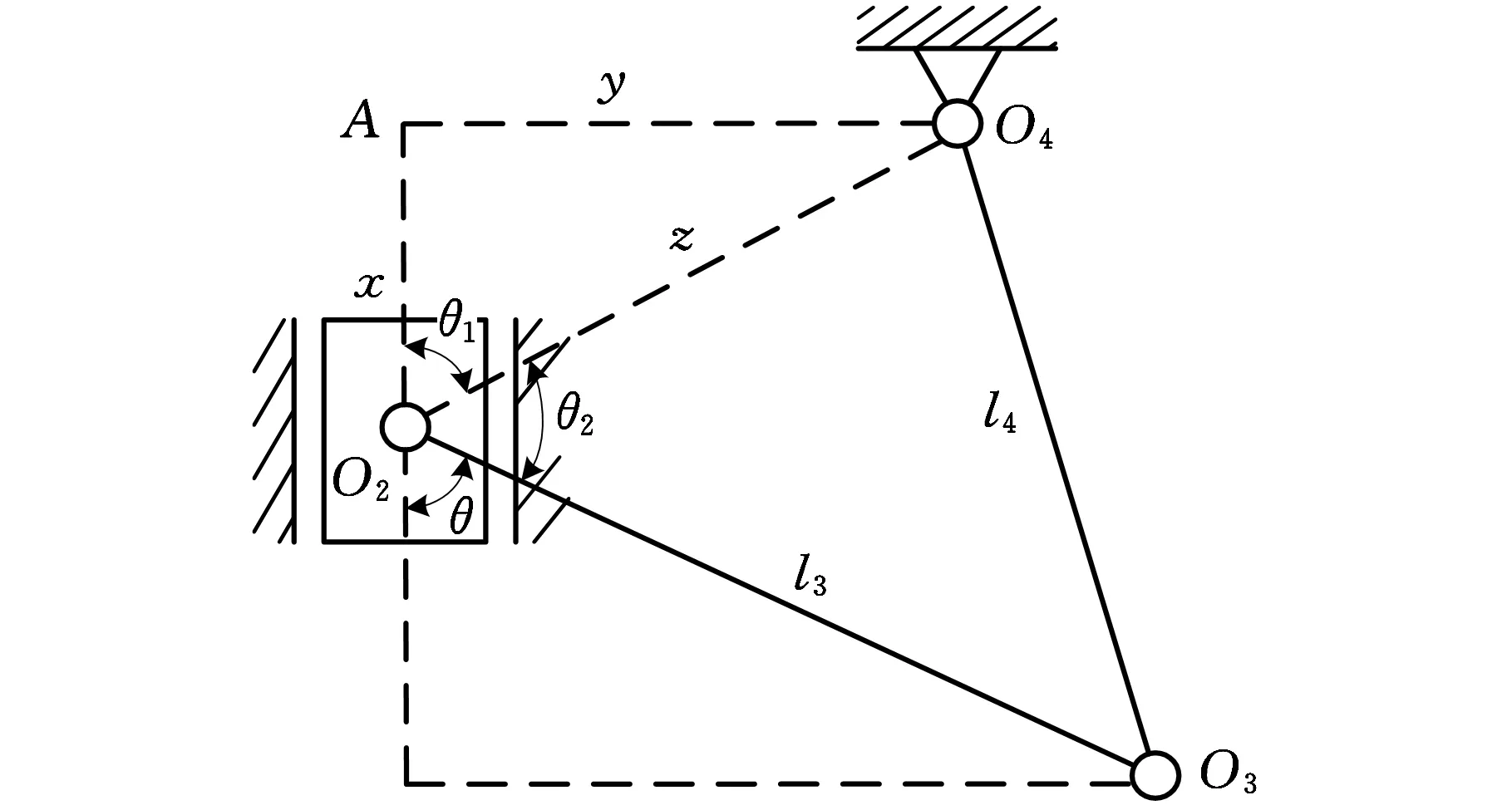
图3　拉杆约束简图

参照图3，并根据各点的位置关系可得

(8)

tanθ1=m/(h-l2+l1)

(9)

(10)

θ=π-(θ1+θ2)

(11)

由拉杆不能处于水平位置，建立姿态约束条件：

g8(X)=π/2-(θ1+θ2)≤0

(12)

(7)为了适应运动副间隙和零件的受力变形，使机构运行可靠且不出现奇异位形，当主滑块处于下死点位置时，必须保证O3点在O4与O5点连线的外侧。

参照图2，根据各杆件的配置方式，当主滑块处于下死点位置时，上下肘杆趋向于共线状态，所以只需约束该状态，即可使上下肘杆不出现共线状态。由图4可得，O2点坐标为(0,l1+l2)，A点坐标为(0,h)，O4点坐标为(m,h)。

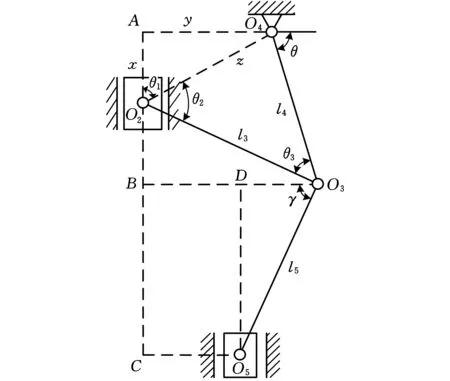
图4　上下肘杆约束简图

根据各点的位置关系可得

(13)

tanθ1=y/x=m/(h-l2-l1)

(14)

(15)

(16)

cosγ=(l3sinθ-n)/l5

(17)

θ=(θ1+θ2+θ3)-π/2

(18)

γ<π-θ

(19)

根据式(19)，建立不等式约束条件：

g9(X)=-cosγ-sin(θ1+θ2+θ3)≤0

(20)

根据加工要求，为保证连杆孔中心距的加工精度，各杆件几何参数必须是整数。在优化程序中加入整数约束条件，可以消除小数圆整带来的误差。2.4优化计算及结果

以正在研发中的某机械式多杆高速压力机单自由度主传动机构为例，考虑其主要用途，根据其主要工艺要求对设计机构的几何参数和运动参数进行多目标综合优化，并与一般机械式高速压力机主传动机构的传动性能进行对比，以验证优化的正确性与合理性。该压力机主传动机构的主要技术参数如下：公称压力为600kN，公称压力行程为3mm，滑块行程为20mm，主滑块最大工作频率为1000次/min。

机械压力机的多杆机构较复杂(杆件数目较多)，且对运动具有较高的要求，采用传统的综合方法效率较低，也不易满足良好的机构综合性能要求。步长搜索法方便易懂，其算法比GA算法、蚁群算法和遗传算法等算法简单，而且可以很好地控制搜索的范围和步长，编程容易，该算法几乎搜遍了全部的解，较容易得到最优解，但是该算法具有较高的时间复杂度，随着计算机技术的发展，该问题已经得到很好的解决，所以本文采用步长搜索法解决多杆机械压力机主传动机构的优化问题。

设计者依据知识和经验给定各参数的取值范围，指定参数变化的优先顺序，确定步长，将设计变量逐一离散化。设计变量共8个，设计变量的离散数最大为k，则可以得到一个用8k阶矩阵表示的变量空间(定义域)S，其中k值的大小直接关系到算法的时间复杂度，所以k值可以先取一个相对较小的值，得到一个最优解，在此基础上k再取较大值，就可以获得较低的时间复杂度。然后在空间S中根据给定的步长搜索，依次从空间下界循环至空间上界，直至最后一个循环中止为止，即遍历空间S的每一组参数。

在对空间S的搜索过程中，并不是所有的点都满足机构运行的约束条件和工程可行性条件。因此，首先对空间中的所有点根据约束条件g1(X),g2(X),…,g9(X)进行判断，满足条件则继续，否则不予计算，进而判断式(1)中的机构性能评价指标f(X)是否取得最小值，直至搜索到空间S的上界。图5为利用步长搜索法对多杆机构优化设计的流程图，其中，stp为步距。

根据上述主要技术参数，利用MATLAB编写优化程序，通过优化得到各杆件的几何参数，即设计变量X的最优解为

X*=(18,300,252,200,248,197,31,316)T

通过运动学分析，得到运动学曲线，如图6～图8所示。

图6所示为两种结构主滑块位移曲线，由图6可知，多杆结构的冲压转角(0.88rad)较一般结构的冲压转角(0.78rad)增大了13.5%，冲压转角的增大使工件材料的变形时间延长，有助于工件材料的充分变形，提高了工件的品质，同时也使机构受力均匀，减小了机构中各构件间的冲击，从而减小了振动。

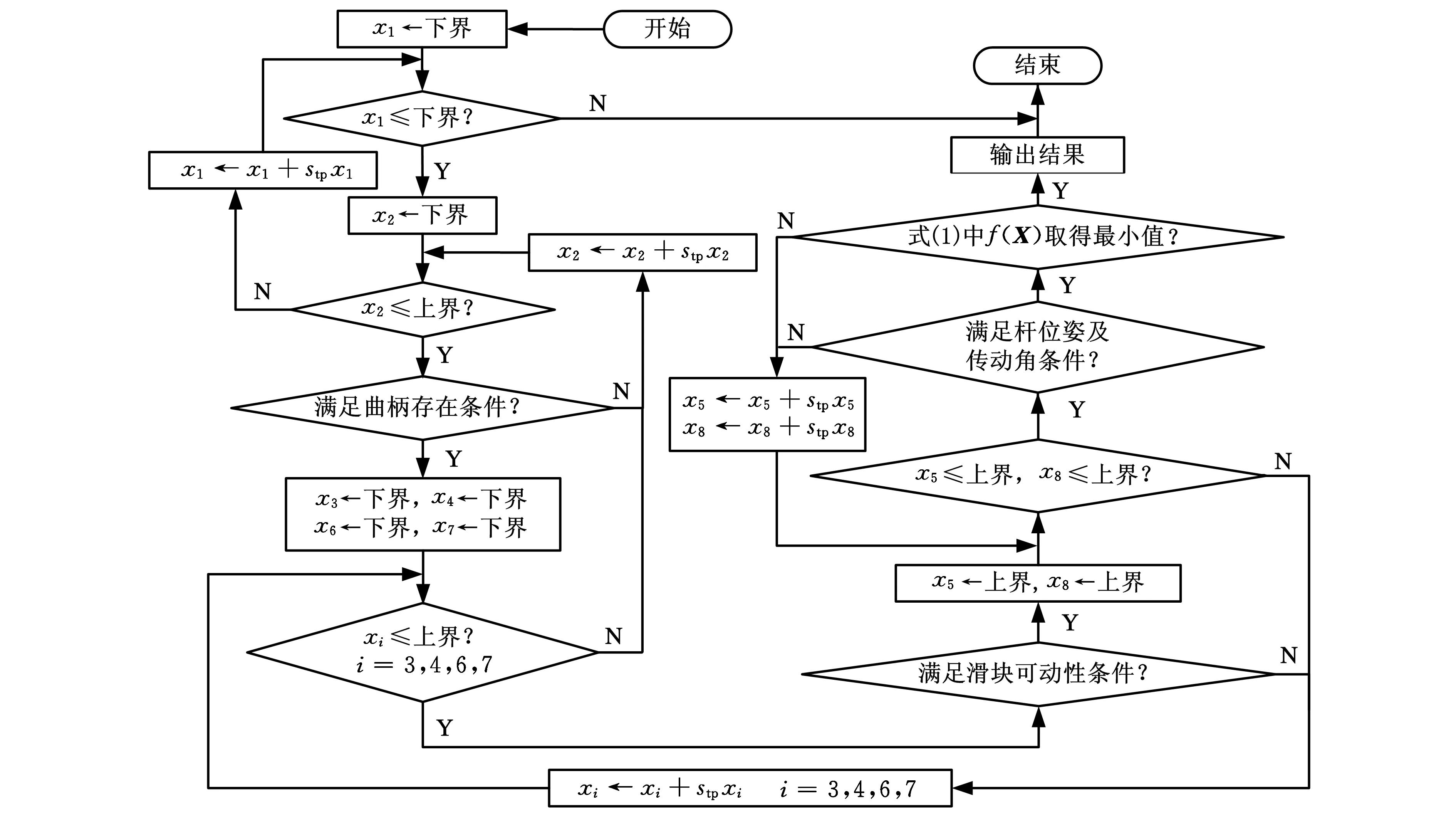
图5　多杆机构优化流程图

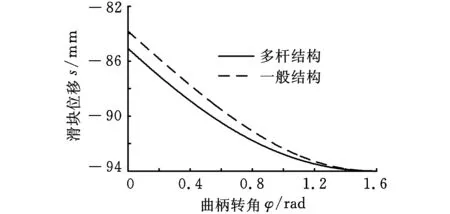
图6　位移曲线

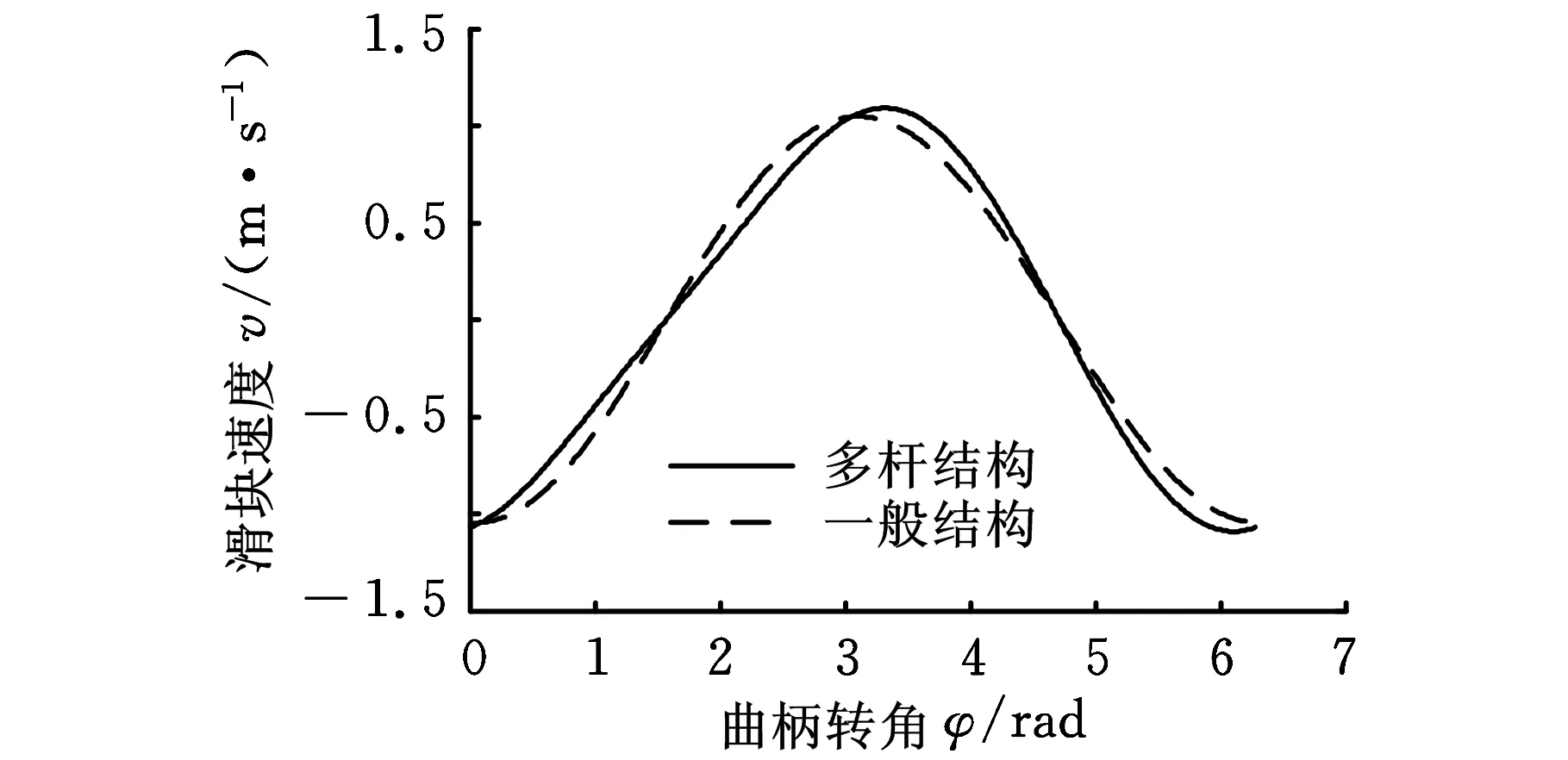
图7　速度曲线

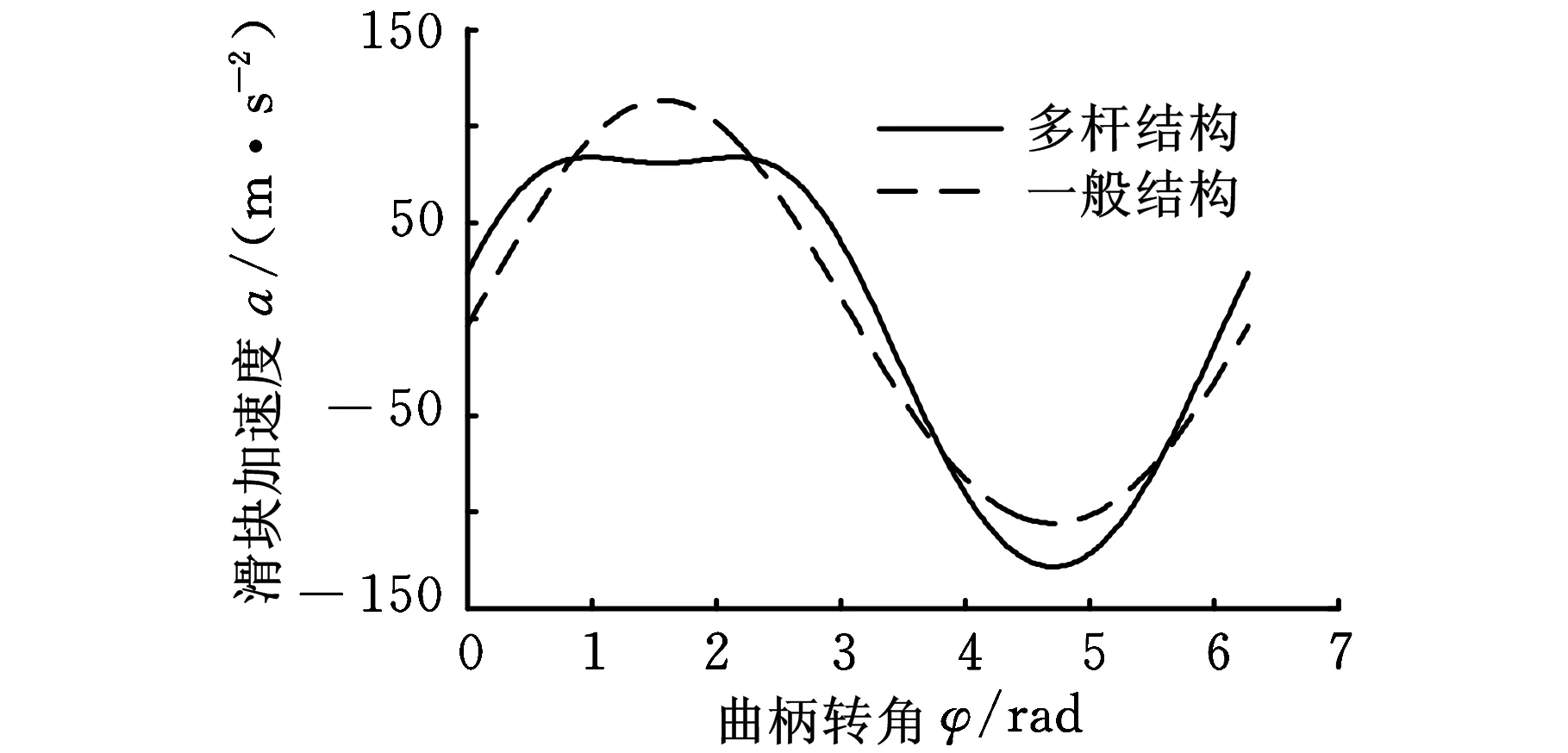
图8　加速度曲线

图7所示为两种结构主滑块速度曲线，由图7可以看出，在0～π段，多杆结构速度曲线的斜率较一般结构的斜率小，速度波动较小，上模接触金属带料时的速度较低，有助于减小冲击和噪声，从而提高压力机的寿命。多杆结构主滑块最大速度较一般结构主滑块最大速度增大了4.1%，该最大值在0.5π～1.5π段回程阶段内，从而缩短了回程时间。

图8所示为两种结构主滑块加速度曲线，由图8可知，多杆结构主滑块加速度较一般结构主滑块加速度减小了35.3%，系统惯性力减小，为动平衡的设计减小了难度，提高了主滑块运动精度，进一步提高了加工的成品率。在下死点附近，多杆结构的主滑块加速度变化较小，近似于保持一定值，这表明主滑块惯性力近似于定值，在压力机冲压阶段主滑块以相对恒定的冲压力冲压工件，上模在接触带料时接触速度减小，加速度和冲压力趋于稳定，从而减小了整机的振动和冲压阶段的冲击，保证了主电机和模具的寿命，以及产品的加工精度。

3　结论

(1)本文通过分析，给出了多杆高速机械压力机的原理传动机构，并建立了机构的多目标优化数学模型，提出了将曲柄长度和冲压转角作为综合评价机构性能优劣的指标。

(2)优化分析结果表明，曲柄长度较小，减小了曲轴的受力和发热，有利于提高机器的运行速度。公称力行程范围内，曲柄转角增大了13.5%，下死点附近位移曲线较平滑，有利于材料的充分变形，利于冲裁。主滑块最大速度增大了4.1%，主滑块最大加速度减小了35.3%，有利于减小机床的振动，提高下死点动态精度。

研究结果为多杆高速机械压力机主传动机构几何参数和运动参数的优化设计提供了参考。

[1]曾梁彬,孙宇,彭斌彬. 基于动态响应的高速压力机综合平衡优化[J].中国机械工程,2010, 21(18): 2143-2148.

ZengLiangbin，SunYu，PengBinbin.SyntheticDynamicBalanceOptimizationofHighSpeedPunchBasedonDynamicResponse[J].ChinaMechanicalEngineering, 2010, 21(18): 2143-2148.

[2]赵升吨,张学来, 高长宇，等.高速压力机惯性力平衡装置及其特性研究(一)[J].锻压设备与制造技术,2005,40(4):27-30.

ZhaoShengdun,ZhangXuelai,GaoChangyu，etal.InvestigationonInertialForceBalanceAssemblyUnitsandTheirDynamicCharacteristicsofaHighSpeedPress[J].ChinaMetalFormingEquipment&ManufacturingTechnology,2005,40(4):27-30.

[3]AzpilgainZ,OrtubayR,BlancoA,etal.Servo-mechanicalPress:aNewPressConceptforSemi-solidForging[J].DiffusionandDefectData:PartBSolidStatePhenomena, 2008, 141/143(3): 261-266.

[4]温庆普.BRUDERER高速冲压技术的优势[C]//第四届中国国际金属成形会议论文集.上海,2008.

[5]HongDK,WooBC,KangDH.ApplicationofFractionalDesignforImprovingPerformanceof60WTransverseFluxLinearMotor[J].JournalofAppliedPhysics, 2008, 103(7):1-3.

[6]王晓丽,周天源.压力机八杆内滑块机构的优化设计[J].农业机械学报, 2007, 38(12): 232-234.

WangXiaoli,ZhouTianyuan.TheOptimizationDesignofInnerSlidingBlockMechanismofEight-barLinkageforPress[J].TransactionsoftheChineseSocietyofAgriculturalMachinery, 2007, 38(12): 232-234.

[7]陈岳云. 多连杆伺服压力机动态性能分析与设计研究[D].上海:上海交通大学, 2008.

[8]李初晔,孙彩霞,郑会恩. 基于ANSYS的多连杆机构性能优化[J].锻压技术,2011,36(6):80-83.

LiChunye,SunCaixia,ZhengHuien.PerformanceOptimizationofMulti-linkageMechanismBasedonANSYS[J].Forging&StampingTechnology,2011,36(6):80-83.

[9]刘海彬. 基于ADAMS的多连杆压力机参数化设计与优化研究[D].青岛:山东科技大学, 2011.

[10]杨春峰,张盛,李云鹏，等. 机械压力机六连杆机构优化设计[J].大连理工大学学报,2013,53(1): 64-70.

YangChunfeng,ZhangSheng,LiYunpeng，etal.OptimizationDesignforSix-barLinkageofMechanicalPress[J].JournalofDalianUniversityofTechnology,2013,53(1): 64-70.

[11]谢嘉, 赵升吨,梁锦涛，等.压力机杆系优化求解的变量循序组合响应面法[J].西安交通大学学报,2012,46(5):57-62.

XieJia,ZhaoShengdun,LiangJintao，etal.VariableSequentialCombinationResponseSurfaceMethodologyforPressRodSystemOptimization[J].JournalofXi’anJiaotongUniversity,2012, 46(5):57-62.

[12]李辉,张策,孟彩芳. 基于正运动学分析的混合驱动压力机优化设计[J].中国机械工程,2004, 15(9): 771-774.

LiHui,ZhangCe,MengCaifang.OptimumDesignofHybrid-drivenMechanicalPressBasedonForwardKinematicsAnalysis[J].ChinaMechanicalEngineering,2004, 15(9): 771-774.

[13]ShangWanfeng,ZhaoShengdun,ShenYajing.AFlexibleToleranceGeneticAlgorithmforOptimalProblemswithNonlinearEqualityConstrains[J].AdvancedEngineeringInformatics, 2009, 23(6): 253-264.

[14]宋清玉,李建, 殷文齐. 基于多目标的机械压力机六连杆机构设计[J].农业机械学报,2012, 43(4): 225-229.

SongQingyu,LiJian,YinWenqi.MechanicalPressSix-linkMechanismDesignBasedonMulti-objective[J].TransactionsoftheChineseSocietyofAgriculturalMachinery,2012, 43(4): 225-229.

[15]林伟庆,李振石,李建平，等. 基于遗传算法的多连杆压力机运动优化方法[J].锻压技术,2011, 36(5): 81-84.

LinWeiqing,LiZhenshi,LiJianping，etal.OptimizationMethodforMovementofMulti-barPressBasedonGeneticAlgorithm[J].Forging&StampingTechnology,2011, 36(5): 81-84.

(编辑陈勇)

Optimization Design for Multi-linkage of High-speed Mechanical Press

Li YejianSun YuHu Fengfeng

Nanjing University of Science and Technology,Nanjing,210094

In order to exert the ability of press, and solve a series of problems of high-speed mechanical press, an compound optimal mathematic model about geometric parameters of main driving organization of high-speed mechanical press was established, which took minimum of crack and maximum of punching angle as the evaluation index. In the meantime, the optimal model was established with MATLAB. The optimization results show that the punching angle of organization is increased by 13.5%, and acceleration of main slider is decreased by 35.3%. The displacement curve is smooth in the near of bottom dead center. It is beneficial to a bundant deformation of materials in the process of stamping, the design of dynamic balance, and to improve the dynamic precision of the bottom dead center.

high-speed press; multi-linkage; optimization design; motion path

2013-08-20

国家科技重大专项(2013ZX04002-082)；江苏省科技支撑计划资助项目(BE2012174)

TH112< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.01.006

李烨健，男，1987年生。南京理工大学机械工程学院博士研究生。主要研究方向为先进制造工艺及装备。发表论文2篇。孙宇，男，1964年生。南京理工大学机械工程学院教授、博士研究生导师。胡峰峰，男，1988年生。南京理工大学机械工程学院博士研究生。