压电谐波传动系统活齿传动自由振动分析
李 冲 许立忠 邢继春
燕山大学,秦皇岛,066004
压电谐波传动系统活齿传动自由振动分析
李冲许立忠邢继春
燕山大学,秦皇岛,066004
提出了一种具有低速大转矩特性的机电集成压电谐波传动系统,该传动系统利用活齿传动输出转矩。分析了机电集成压电谐波传动的工作原理,建立了活齿传动动力学模型,推导了其动力学微分方程,给出了活齿传动自由振动特征方程,求出了系统固有频率及振型,并分析了结构参数对固有频率的影响。研究结果为机电集成压电谐波传动系统的进一步优化提供了新的思路和方法。
压电谐波传动;活齿传动;自由振动;模态分析
0 引言
近年来,我国能源、交通、航空和军事等领域的发展,对机械传动系统的精度、效率、微型化和功率密度等提出了更高的要求,在这一趋势下,基于压电陶瓷等材料的集机械、力学、电学和控制等多学科交叉的新型驱动成为研究的热点[1-3]。传统压电电机以定转子间的摩擦传动为主,其缺点是接触面磨损严重、寿命短且能量损耗严重[4-6]。非接触式压电电机虽然避免了摩擦,但其输出力矩小,承载能力低[7]。20世纪90年代,Ishida等[8]提出了一种利用应变波传动的摩擦型压电电机,该传动类似于谐波电机。2000年,Oliver[9]提出了一种利用谐波齿轮箱和8个压电堆传动的谐波压电电机,该电机用齿轮箱的柔轮代替了传统的行波发生器。2004年,辛洪兵等[10]利用位移放大机构设计了一台压电谐波电机。以上几类谐波电机大多采用谐波齿轮传动方式,柔轮承受较大的交变载荷,对柔轮材料的抗疲劳强度、加工等要求较高,且谐波齿轮传动比下限值较高。
本文提出了一种既能降低摩擦损耗、延长电机寿命,又能增大电机输出力矩的机电集成压电谐波传动系统。该传动系统利用活齿啮合取代定转子之间的摩擦力来驱动转子,从而实现系统要求的大传动比和大力矩,并保证转速稳定。活齿传动是一种要求较严格的传动,在传动过程中极易产生振动,活齿构件的振动往往会对传动系统的稳定性产生影响。梁尚明等[11]建立了摆动活齿传动系统的动力学模型。金向阳等[12]对航空用微小型正弦活齿系统的扭转振动动力学进行了研究和分析。本文针对机电集成压电谐波传动系统活齿传动建立了动力学模型,并推导了其动力学方程。
1 压电谐波传动系统工作原理
图1为压电谐波传动系统结构及原理图。图1c中,该系统以互为90°夹角的两路压电堆作为驱动源,初始时刻由于压缩弹簧的作用,各构件之间无间隙接触且摆动体朝压电堆方向存在一定的偏移量;当给两路压电堆输入相位差为90°且带有正偏置的正弦信号后,压电堆产生沿轴向伸长的变形量,该变形量通过弹性体的作用推动摆动体朝弹簧一侧摆动;当正弦信号处于零电势时摆动体通过弹簧的作用恢复到初始位置。相位差为90°的两路信号同时作用时,两方向的往复摆动在波发生器边缘处就形成了连续谐波。由于弹性体和摆动体都具有位移放大作用,波发生器边缘处可获得压电堆伸长量几十倍的偏移量(a)。将上述谐波通过活齿传动输出,取样机活齿数为30,中心轮波齿数为29,便获得传动比为30的机电集成压电谐波传动。
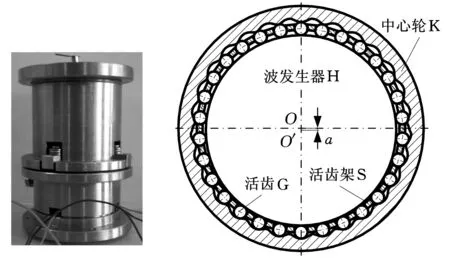
(a)样机装配图(b)活齿传动模型图
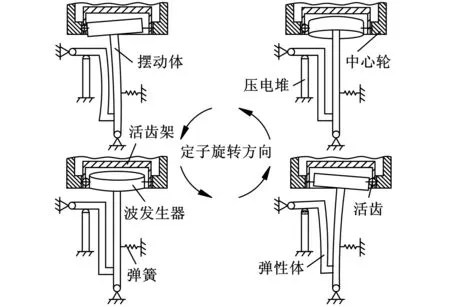
(c)工作原理简图图1 压电谐波传动系统结构及原理图
2 动力学模型的建立
2.1动力学模型
压电谐波传动系统活齿传动部分由波发生器、活齿架、活齿、中心轮等零件构成,借鉴行星轮传动扭转振动的研究成果[13],建立活齿传动自由振动动力学模型。在动力学分析中作以下假设:
(1)活齿传动不受轴向力,假设每个构件都在垂直于轴线的平面内振动,且活齿只考虑平移振动。
(2)主要构件简化为刚体,各构件啮合处简化为弹簧,中心轮、波发生器与活齿之间啮合处简化为作用在啮合法线方向上的线性弹簧。
(3)各活齿的质量、转动刚度和啮合刚度相同。
(4)不计阻尼及啮合处的摩擦力。
动力学模型如图2所示,OXY为固定坐标系,Oxy为活齿架坐标系,oixiyi为各活齿坐标系,i=1,2,…,z,其中z为活齿个数。活齿架坐标系随活齿架以角速度ωr等速转动,活齿坐标系随活齿架坐标系一起等速转动,活齿坐标系原点位于活齿中心。活齿、活齿架、中心轮和波发生器分别用下标p、r、c、s表示。图2中,uj表示各构件线位移,θj为构件j因系统振动而产生的角位移,则uj为
uj=rjθjj=r,c,s,p1,p2,…,pf,p(f+1),…,pz
(1)
式中,rj为各构件理论半径,m;f为啮合活齿数。

图2 动力学模型
每个构件j的位移向量qj以及与qj相应的质量矩阵Mj定义为
(2)
Mj=diag(mj,mj,Ij)
(3)
式中,mj、Ij分别为各构件的质量和等效质量,kg;xj、yj分别为各构件在x和y方向的振动位移,m。
2.2各构件加速度
假设各构件振动位移矢量r在固定坐标系OXY中的坐标分量分别为X、Y,在活齿架动坐标系Oxy中的坐标分量分别为x、y,则有
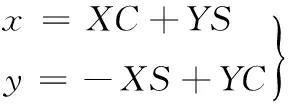
(4)
式中,C、S为常量。
由式(4)可得到在活齿架动坐标系中各构件j中心处的加速度分量:
(5)
式中,ωr为活齿架转角。
2.3各构件相对位移
图3所示为各构件啮合处的相对位置关系,设由波发生器指向活齿的方向为波发生器相对于活齿沿啮合线的正方向,则波发生器相对于活齿的位移沿啮合线方向的投影为
δsk=(Xs-xpi)cos(φk+φ3k)+
(Ys-ypi)sin(φk+φ3k)+ussinφ3k
(6)
式中,xpi、ypi分别为第i个活齿在x和y方向的线位移,m;Xs、Ys为波发生器在X和Y方向的线位移,m;us为波发生器沿圆周方向的线位移,m;φk为第i个活齿中心与活齿架中心的连线与固定坐标系中X轴正方向的夹角;φ3k为波发生器中心和第i个活齿中心连线与第i个活齿中心和活齿架中心连线的夹角。
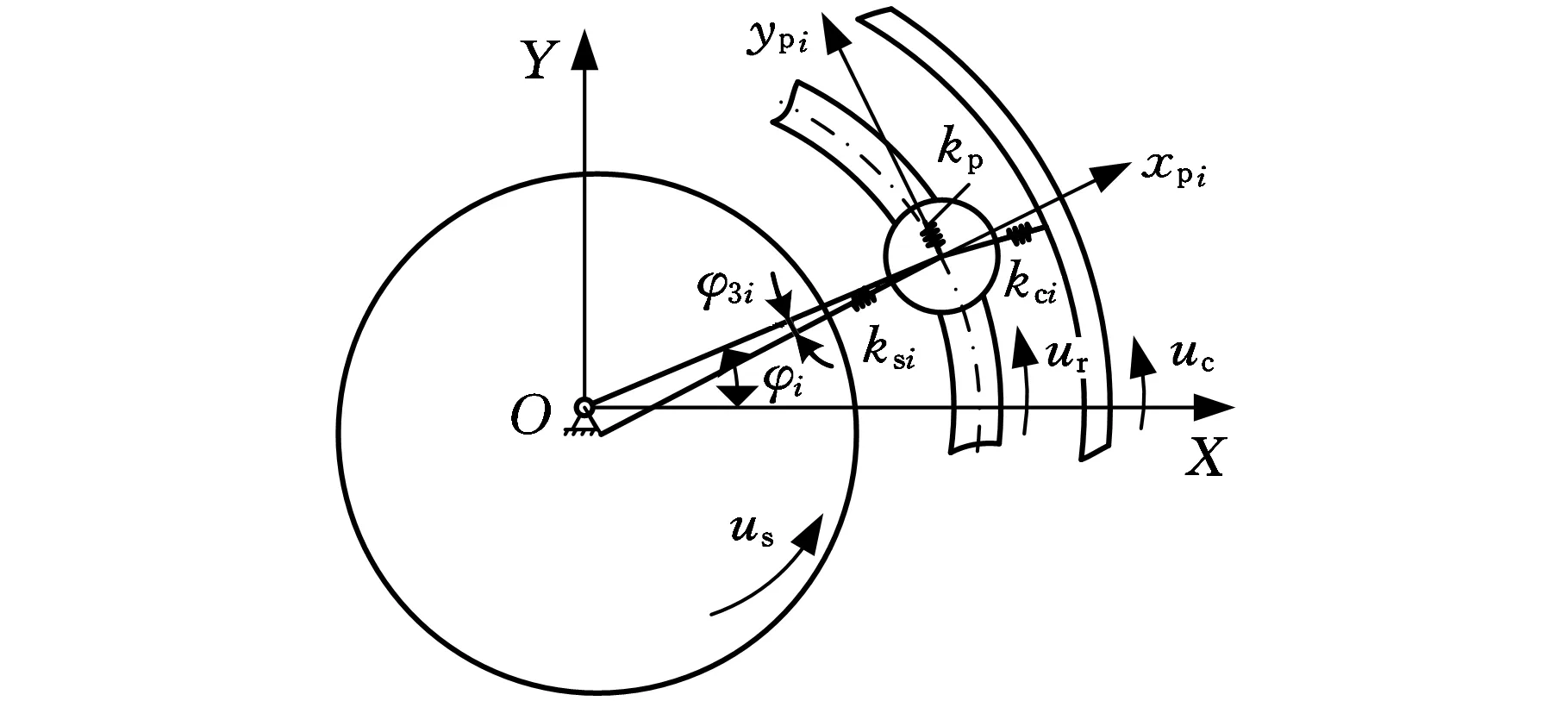
图3 各构件相对位移
设由活齿指向中心轮的方向为中心轮相对于活齿沿啮合线的正方向,则活齿相对于中心轮的位移沿啮合线方向的投影为
δck=(xc-xpi)cosθi+(yc-ypi)sinθi-ucsin(φk-θi)
(7)
式中,xc、yc分别为中心轮在x和y方向的线位移,m;uc为中心轮沿圆周方向的线位移,m。
活齿架相对于活齿的位移沿活齿架切向的投影为
δr i t=(xpi-xr)sinφk+(yr-ypi)cosφk-ur
(8)
式中,xr、yr分别为活齿架在x和y方向的线位移,m;ur为活齿架沿圆周方向的线位移,m。
2.4各构件动力学微分方程
由波发生器与活齿啮合处的相对位移关系,建立波发生器动力学微分方程:
(9)
k=1,2,…,fl=f+1,f+2,…,z
式中,ks、ksz、kst分别为活齿与波发生器的啮合刚度、波发生器径向支撑刚度和切向扭转刚度,N/m;δsk、δsl分别为波发生器相对于工作活齿和非工作活齿的位移沿啮合线方向的变形量,m。
由中心轮与活齿啮合处的相对位移关系,运用牛顿定律建立中心轮动力学微分方程:
(10)
式中,kc、kcz、kct分别为活齿与中心轮的啮合刚度、中心轮径向支撑刚度、切向扭转刚度,N/m;δck、δcl分别为工作活齿和非工作活齿相对于中心轮的位移沿啮合线方向的变形量,m。
由活齿架与活齿啮合处的相对位移关系,建立活齿架动力学微分方程:
(11)
式中,kp、krz、krt分别为活齿与活齿架之间的啮合刚度、活齿架径向支撑刚度和切向扭转刚度,N/m;δr k t、δr l t分别为活齿架相对于工作活齿和非工作活齿的位移沿啮合线方向的变形量,m。
由活齿与各构件啮合处的相对位移关系,建立活齿动力学微分方程:
(12)
2.5系统动力学微分方程
由于机电集成压电谐波传动系统工作在低速,ωr较小,故动力学方程中可以略去与ωr有关的量,由式(9)~式(12)可得简化后的系统动力学方程:
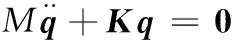
(13)
q=[xsysusxcycucxryrurxp1yp10 …xpzypz0]T
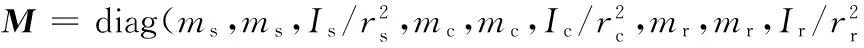
K=
其中,各矩阵和列阵的维数都是3Z+9,q为系统的广义坐标列阵;M为质量矩阵,是对角矩阵;K为刚度矩阵。
式(13)对应的特征方程为
(14)
式中,ωh为系统各阶固有频率;φh为振型矢量。
3 结果分析与讨论
3.1固有频率求解与分析
系统参数见表1,取样机的传动比为30,将表1中参数代入式(14),得到当啮合活齿数为15和16时的部分固有频率(表2),表2中m表示固有频率的重根数,z=30。
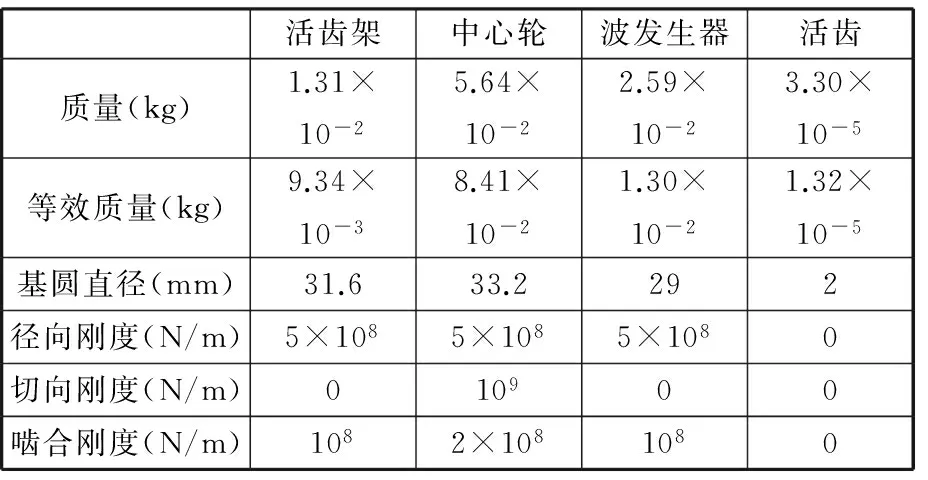
表1 活齿传动系统参数
表2活齿系统部分固有频率及振型

啮合活齿数为15时(rad/s)啮合活齿数为16时(rad/s)系统全振动m=12061、414882093、60582波发生器平移振动m=194191、142093347066、3018793中心轮静止振动m=11746511、17576091746780、1758777全部活齿平移振动m=11740416、17404401742268、1742466啮合活齿直线振动m=1030151133015113啮合活齿直线振动m=1117407761740776系统刚体运动m=z00固有频率总数9999
由表2可知:
(1)活齿传动自由振动固有频率总数恒定为3z+9个,由1个频率为0的z重根和2z+9个非零根组成,活齿总数为30时共有99个固有频率。
(2)不论啮合个数是15还是16,固有频率均有3 015 113 rad/s和1 740 776 rad/s的非零重根值,重根数都是m=10和m=11,且非零重根出现时的振动模态都是啮合活齿直线振动模态。
(3)活齿传动差齿个数为1时,固有频率为0的振动模态是以刚体的形式运动的,且固有频率0的重根数等于活齿个数z。
(4)活齿传动自由振动中共出现5种振动模态,分别是系统全振动模态、波发生器平移振动模态、中心轮静止振动模态、全部活齿平移振动模态以及啮合活齿直线振动模态。出现次数最多的是全部活齿平移振动模态,出现次数是32。
3.2振型分析与讨论
选取表2中啮合活齿数为16的部分固有频率值代入式(14),可求得部分模态振型。系统各振动模态如图4所示,其中图4a为系统全振动模态,图4b为波发生器平移振动模态,图4c为中心轮静止振动模态,图4d为全部活齿平移振动模态,图4e和图4f为啮合活齿直线振动模态。其中正负号表示相应的振动方向。由图4中得出以下规律:
(1)每一个单重根固有频率对应一种振型,在系统全振动模态对应的振型中,波发生器、中心轮和活齿架的线位移和沿圆周方向的角位移均不为0,既能平移振动又能旋转振动,活齿沿x、y方向的线位移不为0,沿圆周方向的角位移为0,只能产生平移振动,不能产生旋转振动。
(2)波发生器平移振动模态中,波发生器沿圆周方向的角位移为0,沿x、y方向的线位移不为0,其他构件各位移不为0。在中心轮静止振动模态中,中心轮的平移振动位移和旋转位移均为0,活齿架的平移振动位移和旋转位移均为非零数值,活齿在平面内平移振动。
(3)在全部活齿平移振动模态对应的振型中,中心轮和活齿架的线位移和角位移均为0,此时只有活齿存在振动,活齿的线位移为非零值,角位移为0,活齿在平面内产生平移振动。当固有频率为10重根3 015 113rad/s和11重根1 740 776rad/s时,活齿传动只有部分啮合活齿处于振动状态,且对应的振动模态都是直线振动。

(a)ω31=2093 rad/s (b)ω39=347 066 rad/s(c)ω67=1 758 777 rad/s
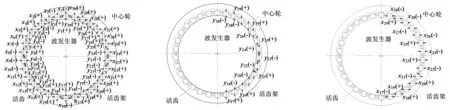
(d)ω62=1 742 466 rad/s (e)ω47=1 740 776 rad/s(f)ω88=3 015 113 rad/s图4 活齿传动系统各振动模态图
3.3参数对固有频率的影响
改变系统的结构参数,分析结构参数对固有频率的影响规律。图5~图7所示为固有频率随结构参数变化曲线。结构参数对中心轮静止模态和啮合活齿振动模态影响较小,因而未给出曲线,由图5~图7可得出以下结论:
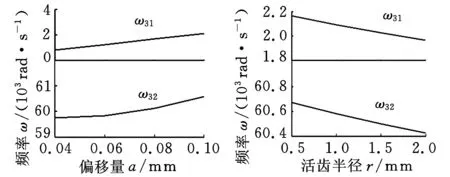
(a)偏移量a的影响(b)活齿半径r的影响
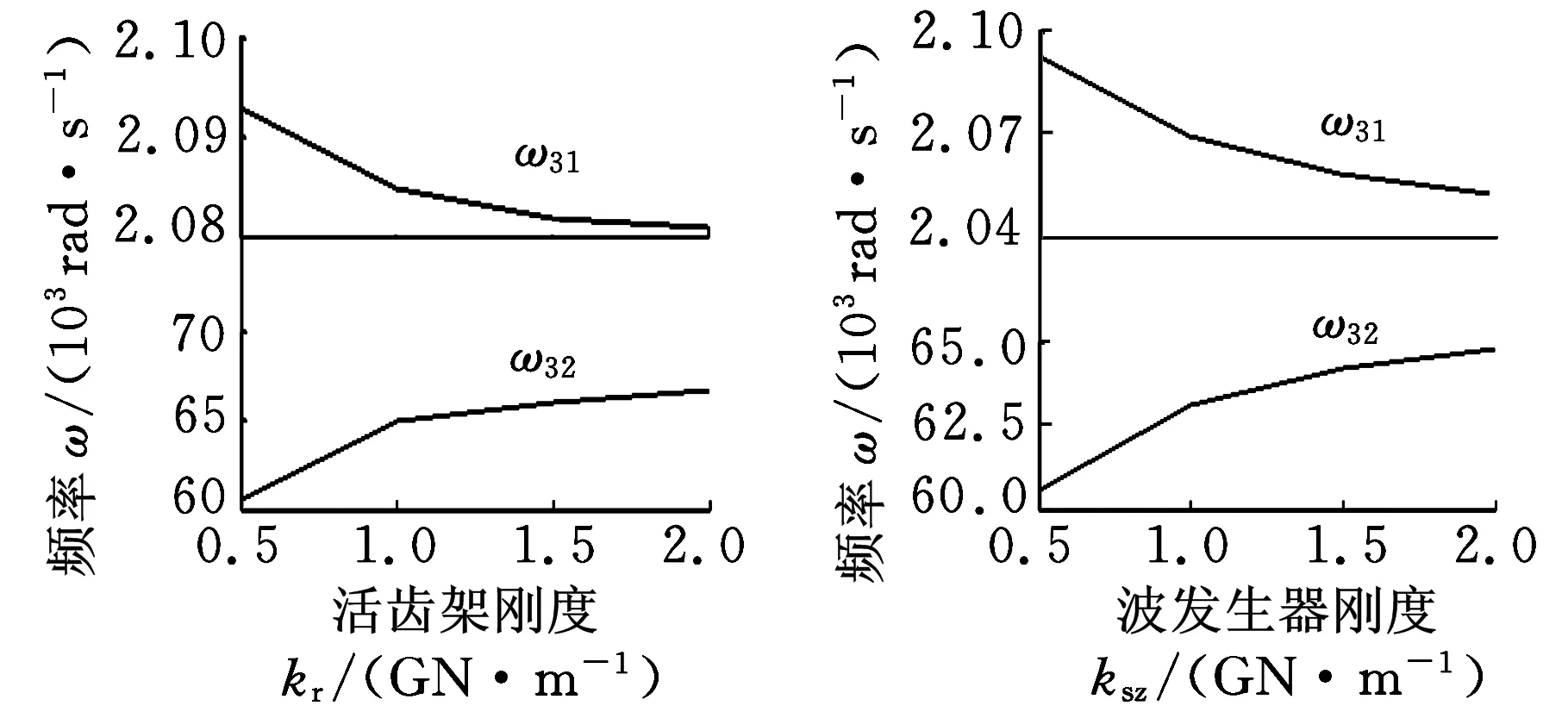
(c)活齿架支撑刚度kr的影响(d)波发生器支撑刚度ksz的影响图5 系统全振动模态参数对固有频率的影响

(a)偏移量a的影响(b)活齿半径r的影响
(1)系统全振动模态中,31阶、32阶固有频率都随偏移量的增大而增大,随活齿半径的增大而减小;活齿架支撑刚度和波发生器支撑刚度对不同阶固有频率的影响不同,31阶固有频率随支撑刚度增大而递减,32阶固有频率随支撑刚度增大而递增,可见支撑刚度对不同阶固有频率的影响具有不确定性。
(2)波发生器平移振动模态中,偏移量对固有频率的影响显著,固有频率随偏移量的增大非线性减小;活齿半径对固有频率有一定影响,固有频率与活齿半径成正比;活齿架和波发生器支撑刚度对曲线变化的影响不明显,对固有频率的影响较小。
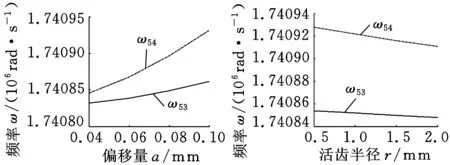
(a)偏移量a的影响(b)活齿半径r的影响

(c)活齿架支撑刚度kr的影响(d)波发生器支撑刚度ksz的影响图7 全部活齿平移振动模态参数对固有频率的影响
(3)全部活齿平移振动模态中,偏移量和活齿半径对固有频率的影响较明显,固有频率随偏移量的增大而增大,随活齿半径的增大而减小;活齿架和波发生器支撑刚度对固有频率的影响不明显。
4 实验验证
对样机进行固有频率测试,采用SZCJ锤击法振动测试系统,在活齿传动系统输出轴处制作一个电容传感器,通过对样机施加激励,使电容间隙发生改变,电容的改变经过测试系统的信号处理后在计算机上显示出固有频率。振动测试系统如图8所示。

图8 振动测试系统
振动测试曲线如图9所示,得到的共振频率分别为375Hz、5534Hz、9771Hz、12 651Hz,对应的理论计算频率分别为2 093rad/s(333Hz)、41 488rad/s(6606Hz)、60 582rad/s(9647Hz)、106 758rad/s(17kHz)。实验结果和理论推导结果误差分别为12.6%、16.2%、1.3%、25.6%,可看出前几阶固有频率误差较小,从而验证了理论推导的正确性。
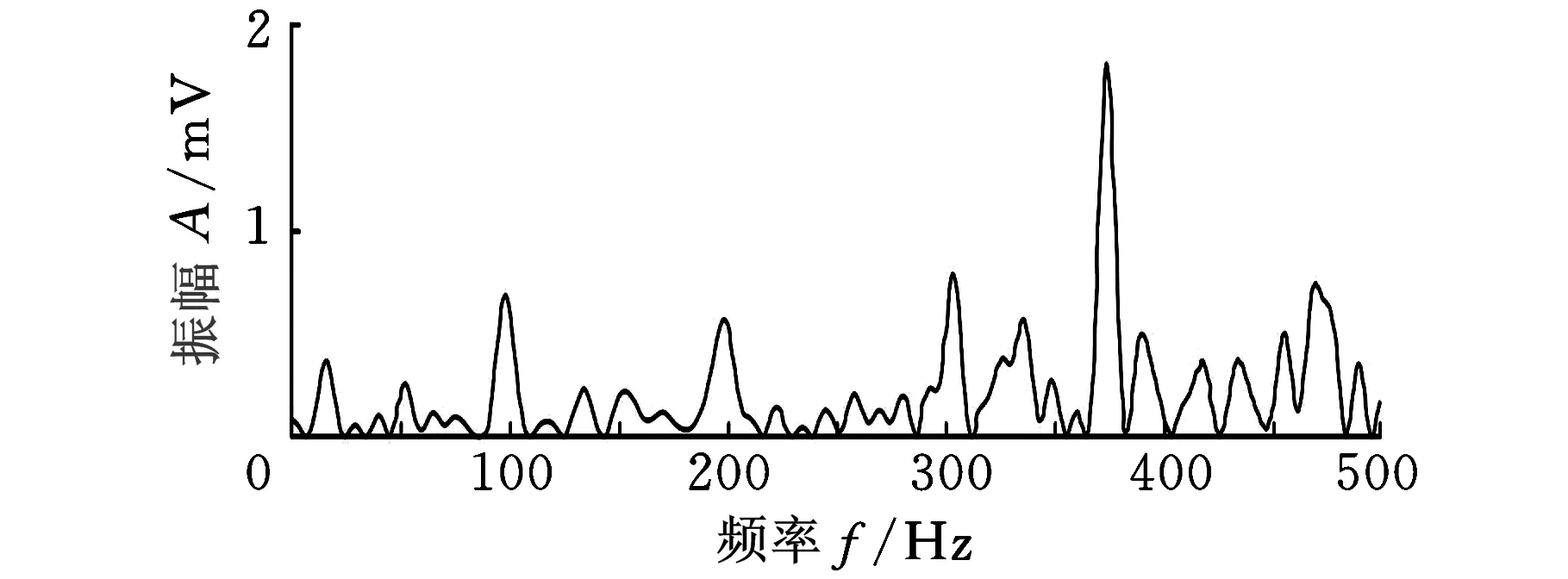
(a)0~500 Hz测试曲线
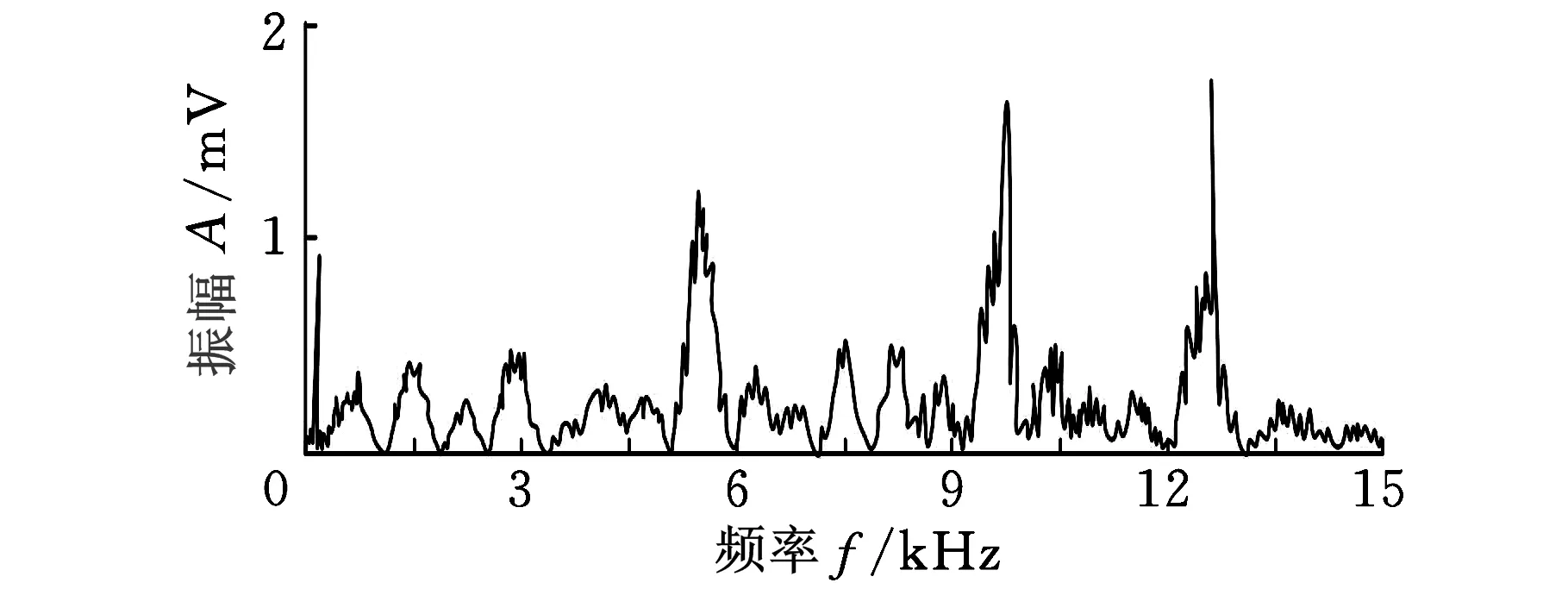
(b)0~15 kHz测试曲线图9 振动测试频率曲线
5 结语
本文在压电驱动和活齿传动的基础上提出了机电集成压电谐波传动系统,建立了活齿传动自由振动模型,推导了其动力学微分方程,求得了系统固有频率及振型,分析了结构参数对固有频率的影响,实验验证了固有频率推导公式的正确性。结果表明:系统全振动模态随结构参数的变化最为明显,波发生器平移振动模态和全部活齿平移振动模态随结构参数变化较小,中心轮静止模态和啮合活齿直线振动模态基本不随参数变化;固有频率对偏移量的变化最为敏感,偏移量是影响固有频率的极其重要的参数。研究结果为机电集成压电谐波传动系统结构优化及性能提高打下了理论基础。
[1]王国彪, 赖一楠, 范大鹏,等. 新型精密传动机构设计与制造综述[J].中国机械工程, 2010, 21(16): 1891-1897.
WangGuobiao,LaiYinan,FanDapeng,etal.SummaryofNewTypePrecisionTransmissionDesignandManufacture[J].ChinaMechanicalEngineering, 2010, 21(16): 1891-1897.[2]PasqualeM.MechanicalSensorsandActuators[J].SensorsandActuatorsA, 2003, 160(1/3): 142-148.[3]秦大同.机械传动科学技术的发展历史与研究进展[J]. 机械工程学报, 2003, 39(12): 37-43.
QinDatong.HistoryandProcessofScienceandTechnologyonMechanicalTransmission[J].ChineseJournalofMechanicalEngineering, 2003, 39(12): 37-43.
[4]WillamsW,BrownW.PiezoelectricMotor:US, 2439499[P]. 1942-08-20.
[5]董蜀湘, 李龙土, 周铁英. 新型驱动器─压电陶瓷马达与展望[J].科技导报, 1996(10): 25-27.
DongShuxiang,LiLongtu,ZhouTieying.ResearchonPoezoceramicMotor[J].Science&TechnologyReview, 1996(10): 25-27.
[6]许海, 赵淳生. 直线型超声电机的发展及应用[J].中国机械工程, 2003, 14(8): 715-717.Xu Hai, Zhao Chunsheng. Development and Application of Linear Ultrasonic Motors[J].China Mechanical Engineering, 2003, 14(8): 715-717.
[7]季叶, 赵淳生. 一种具有高转速的新型非接触式超
声电机[J]. 压电与声光, 2006, 28(5): 527-529.
Ji Ye, Zhao Chunsheng. A New Type Non-contact Ultrasonic Motor with Higher Revolution Speed[J]. Piezoelectrics & Acoustooptics, 2006, 28(5): 527-529.
[8]Ishida M, Hamaguchi J, Shirasuka K,et al. A New Friction-type Piezoelectric Motor Utilizing Mechanism of the Strain Wave Gearing[J].IEEE Transactions on Industrial Electronics, 1992, 39(1):30-35.
[9]Oliver B.Harmonic Piezodrive-miniaturized Servo Motor[J]. Mechatronics, 2000, 10(4):545-554.
[10]辛洪兵, 郑伟智. 压电谐波电机的研究[J].压电与声光, 2004, 26(2):122-125.
Xin Hongbing, Zheng Weizhi. Study on Harmonic Piezomotor[J].Piezoelectrics & Acoustooptics, 2004, 26(2):122-125.
[11]梁尚明, 张均富, 徐礼柜,等.摆动活齿传动系统振动的动力学模型[J].振动工程学报, 2003, 16(3):285-289.
Liang Shangming, Zhang Junfu, Xu Liju, et al. Dynamic Model of Swing Movable Teeth Transmission System Vibration[J].Journal of Vibration Engineering, 2003, 16(3): 285-289.
[12]金向阳, 于广滨, 关祥毅.航空用微小型正弦活齿系统扭转振动动力学分析[J].中北大学学报(自然科学版), 2007, 28(4):299-303.
Jin Xiangyang, Yu Guangbin, Guan Xiangyi. Torsion Dynamics of Aviation Micro Cylinder Sine Oscillating Tooth System[J].Journal of North University of China (Natural Science Edition), 2007, 28(4):299-303.
[13]Xu Lizhong,Zhu Xuejun.Natural Frequencies and Vibrating Modes for a Magnetic Planetary Gear Drive[J]. Shock and Vibration, 2012, 19(6): 1385-1401.
(编辑陈勇)
Free Vibration of Oscillating Tooth Drive for an Electromechanical Integrated Harmonic Piezodrive System
Li ChongXu LizhongXing Jichun
Yanshan University,Qinhuangdao,Hebei,066004
An electromechanical integrated harmonic piezodrive system was proposed, which had the characteristics of low speed and high torque. The system output torque through oscillating teeth. The principles of the electromechanical integrated harmonic piezodrive system were discussed, the dynamic models and dynamic equations were set up. Frequency equations of free vibration of oscillating tooth were given and the natural frequencies and vibration modes were solved, and the impacts of parameters on natural frequencies were analyzed. These results provide basis for the improvement and the further research of the electromechanical integrated harmonic piezodrive system.
harmonic piezodrive; oscillating tooth drive; free vibration; modal analysis
2013-08-26
国家自然科学基金资助项目(51275441)
TH113.1DOI:10.3969/j.issn.1004-132X.2015.01.003
李冲,男,1988年生。燕山大学机械工程学院博士研究生。主要研究方向为机电集成压电谐波传动系统。许立忠(通信作者),男,1962年生。燕山大学机械工程学院教授、博士研究生导师。邢继春,男,1983年生。燕山大学机械工程学院讲师。

