基于遗传算法与BP神经网络的微晶玻璃点磨削工艺参数优化

马廉洁　曹小兵　巩亚东　陈小辉

1.东北大学秦皇岛分校，秦皇岛，0660042.东北大学，沈阳，110819

基于遗传算法与BP神经网络的微晶玻璃点磨削工艺参数优化

马廉洁1,2曹小兵1巩亚东2陈小辉1

1.东北大学秦皇岛分校，秦皇岛，0660042.东北大学，沈阳，110819

通过低膨胀微晶玻璃点磨削实验，测试了加工表面粗糙度、表面硬度，分析了实验数据变化趋势。通过最小二乘拟合，建立了关于粗糙度、表面硬度的一元数值模型，并将模型预测值与实验值进行了比较，以验证模型的精确性，结果表明模型具有较高的精度。根据正交实验结果，基于BP神经网络算法和遗传算法，建立了粗糙度、表面硬度的多元数值模型并以此作为目标函数，以表面硬度最大和表面粗糙度最小作为优化目标，基于遗传算法进行了工艺参数的双目标优化，获得了一组点磨削工艺参数的最优解范围，实验验证结果表明优化结果是合理的。

BP神经网络；参数优化；点磨削；微晶玻璃

0　引言

高速点磨削是一种先进的加工技术，它兼具磨削的高表面质量和车削的高生产效率[1-3]，被认为是脆性材料实现延性域去除的有效方法之一。低膨胀微晶玻璃是一种新型无机材料，在精密仪器、激光技术、航空航天等领域应用前景十分广阔[1-4]。传统方法对低膨胀微晶玻璃进行加工时，难以获得高精密的表面质量，且效率很低[5]。

有关硬脆性材料加工技术的研究主要集中在性能分析、加工机理等方面，由于实验数据的离散化，对加工过程与工艺参数之间内在关系的研究报道较少。遗传算法是一种仿生智能优化算法，对解决高维不可导、不连续问题甚为有效，故其在上述方面应用广泛[6-7]。BP神经网络是多层前馈性神经网络，具有良好的泛化能力，在函数预测、数据挖掘、数值分析等方面有着广阔的应用[8-9]。

本文在点磨削实验数据分析的基础上，根据单因素实验建立了低膨胀微晶玻璃表面硬度和表面粗糙度与工艺系统因素的一元模型，根据正交实验进一步建立了多元模型，采用遗传算法进行了双目标工艺参数优化。

1　实验

实验在MK9025A型曲线磨床上进行，选用陶瓷结合剂CBN砂轮，砂轮直径为180 mm、磨料粒度为200、砂轮浓度为150%、宽度为7 mm、磨料厚度为5 mm。选用低膨胀微晶玻璃为实验材料，其主要性能参数为：密度2.53 g/cm3，体膨胀系数2.0～4.0×10-8/K，抗弯强度173 MPa。磨削后的表面粗糙度Ra在Micromeasurez三维表面轮廓仪(法国)上进行测量，加工表面的显微硬度用FM-ARS9000型全自动显微硬度测量系统进行测量。

通过单因素实验(表1)结合 BP神经网络算法进行了数值拟合，建立了表面硬度、表面粗糙度与工艺参数的一元模型，通过正交实验(表2和表3)，进一步建立了表面硬度、表面粗糙度的多元模型。以表面硬度和表面粗糙度为目标，利用遗传算法对点磨削工艺参数进行了双目标优化。为验证多元模型及优化结果的精确性，设计了表4所示的验证实验进行验证。

表1　单因素实验表

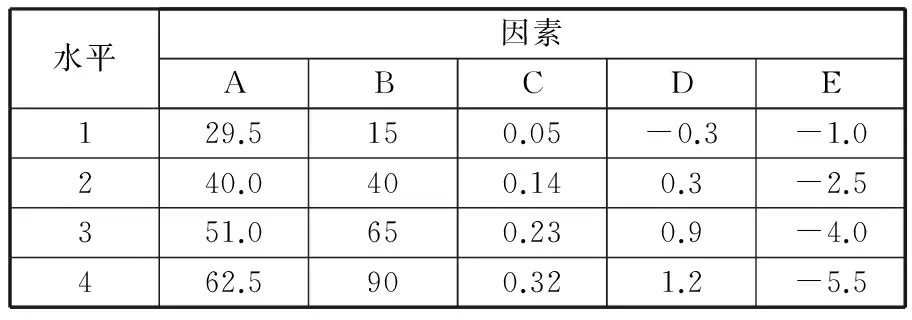
表2　正交实验水平-因素表

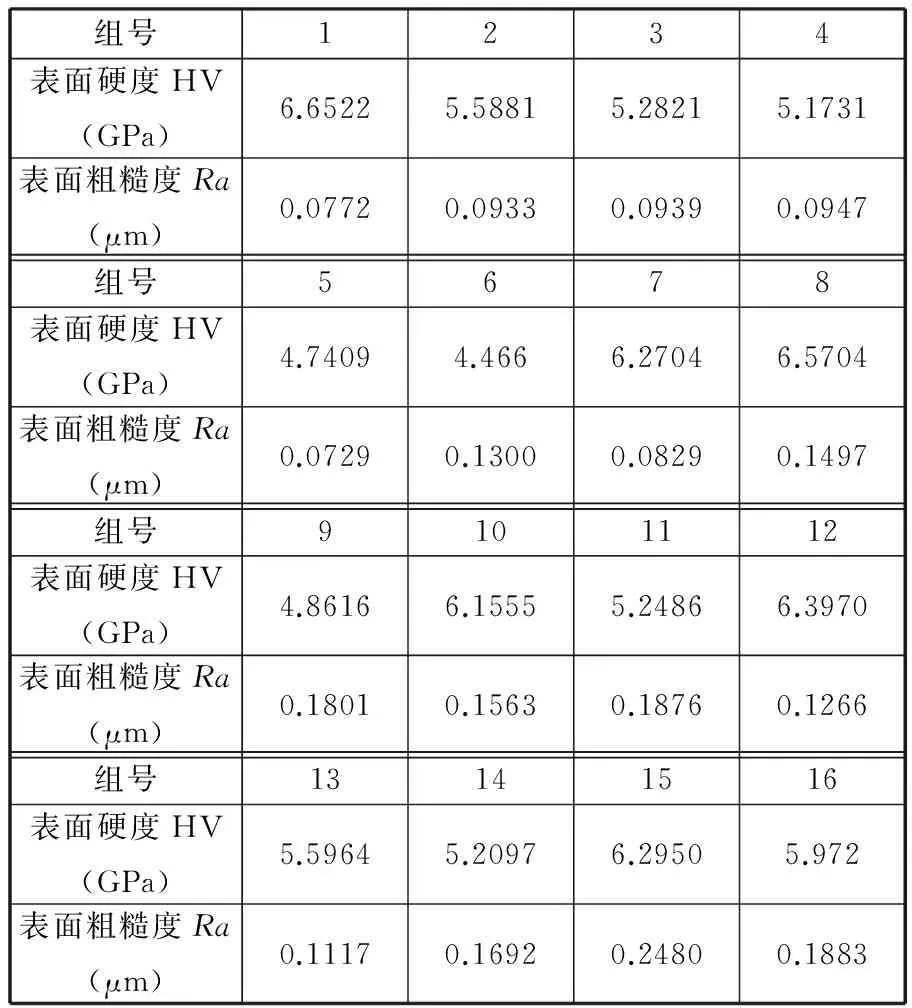
表3　正交实验结果

表4　验证实验

2　神经网络与遗传算法

2.1神经网络理论

BP神经网络是一种多层前向型神经网络，一般包含一个输入层、一个或多个隐含层和一个输出层，上下层之间全互连，同层节点之间互不相连。BP神经网络算法的数学理论如下：

设输入层节点为X=(x1,x2…,xm)，隐含层节点为P=(p1,p2,…,pd)，输出层节点为Y=(y1,y2,…,yn)，输出层期望向量为S=(s1,s2,…,sn)，隐含层的阈值向量为B=(b1,b2,…,bd)，输出层阈值向量为C=(c1,c2,…,cn)，输入层与隐含层间的网络权值为wij,隐含层与输出层间的网络权值为wjk，其中,i=1,2,…,m;j=1,2,…,d;k=1,2,…,n，则隐含层节点输出为

(1)

netj=wijxi-bj

式中，f(·)为激活函数。

输出层输出为

(2)

netk=wjkpj-ck

输出层误差函数为

(3)

基于误差函数对输出层各节点求偏导可得

(4)

基于输出层的δk与隐含层的误差函数，对隐含层各节点求偏导可得

(5)

基于输出层的δk与隐含层的θj，对权值wij和wjk进行修正，其最终的总误差计算表达式为

(6)

至此，BP神经网络完成一次学习过程，当误差达到预设精度时，算法结束，否则，进入下一轮学习，直至误差达到预设精度为止。

2.2遗传算法理论

遗传算法是一种基于生物遗传与进化机制的智能仿生优化算法，可以把问题参数编码为染色体，利用选择、交叉、变异等操作使种群中的染色体进化到搜索空间中越来越好的区域，最后收敛于符合优化目标的染色体。算法流程图见图1。

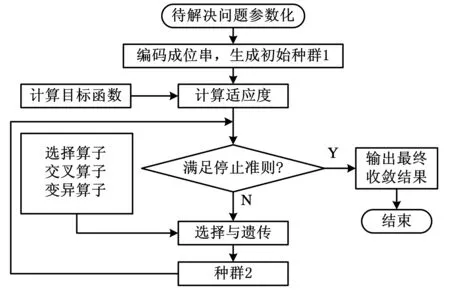
图1　遗传算法流程图

3　表面质量数值拟合

3.1表面硬度HV单因素数值拟合

图2所示为砂轮速度对表面硬度的影响。基于实验值与BP神经网络预测值，通过数值拟合，可解得表面硬度与砂轮速度vc的模型表达式：

H=-0.7832e-3.195×10-3(vc-41)2+5.585

(7)

式中，H为表面硬度HV。

式(7)中的模型决定系数R为0.9459。同理，表面硬度与进给率f、磨削深度ap、倾斜角α、偏转角β的数值模型可分别表示为

H=-111.1e6.02×10-6(f-22.1)2+117.3

(8)

(9)

H=0.4269αe-0.04111α2+6.11

(10)

H=-0.2686βe-0.0153β2+6.382

(11)

图2　砂轮速度对表面硬度的影响

式(8)～式(11)模型的决定系数R分别为0.9435、0.8535、0.946、0.8936。图3～图6所示分别为f、ap、α、β参数对表面硬度的影响曲线。

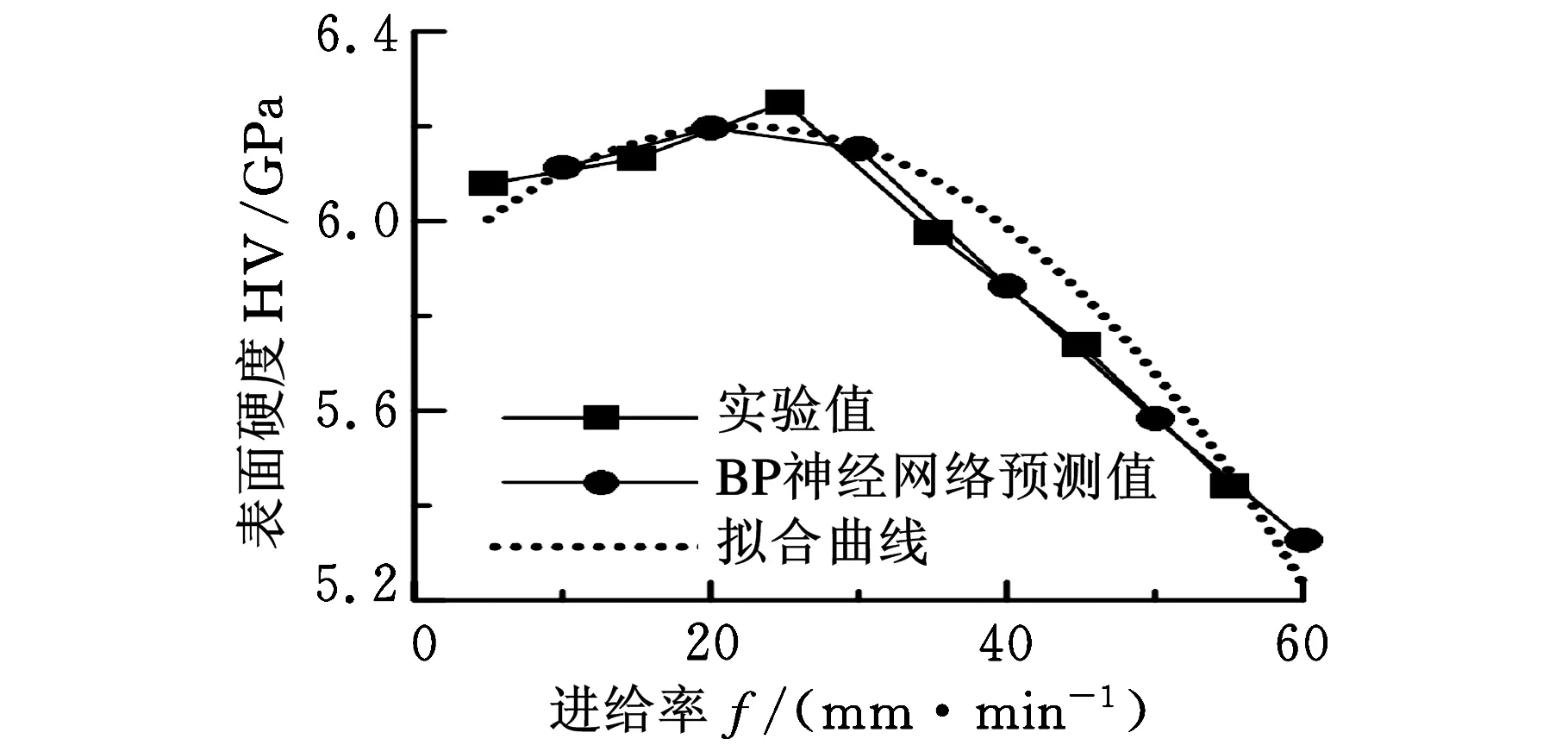
图3　进给率对表面硬度的影响

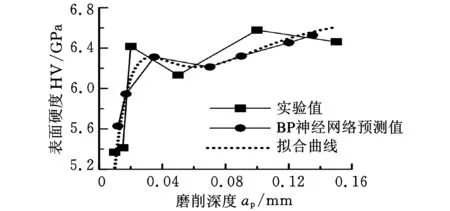
图4　磨削深度对表面硬度的影响

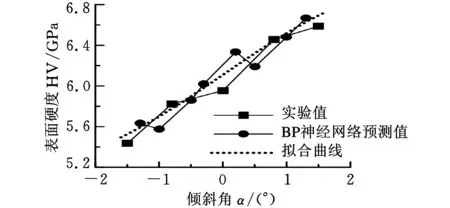
图5　倾斜角α对表面硬度的影响

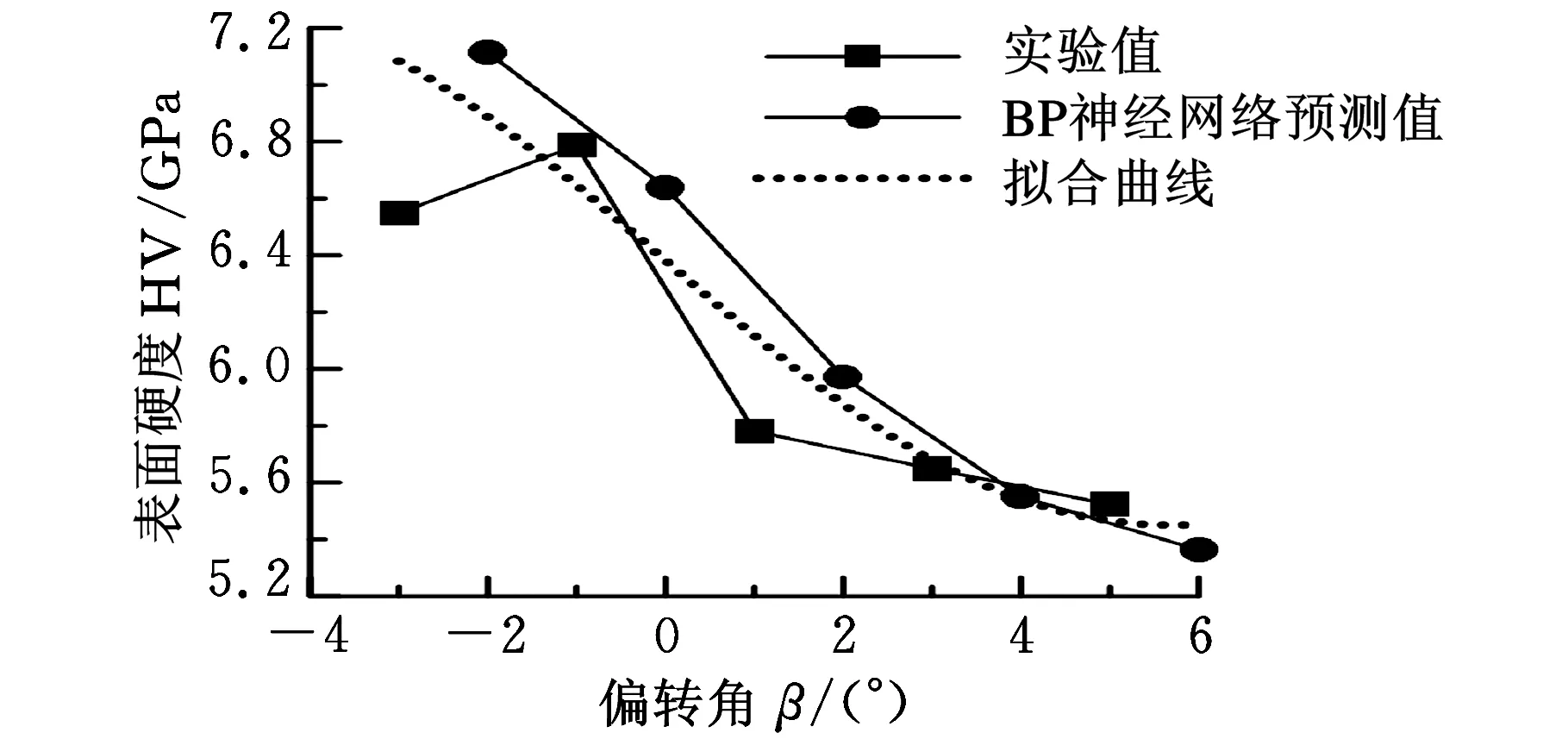
图6　偏转角β对表面硬度的影响

3.2表面硬度多元模型

3.2.1模型假设

基于单因素数值拟合结果(式(7)～式(11))，提出了低膨胀微晶玻璃点磨削表面硬度关于点磨削参数的多元模型，其数学表达式为

(12)

式中，a、b、c、d均为常数。

3.2.2模型求解

模型求解的适应度准则为

(13)

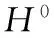
建立的表面硬度与点磨削参数模型表达式为

(14)

根据正交实验(表2和表3)，基于遗传算法对模型进行优化求解，以多元模型与正交实验值的方差最小为适应度准则(式(13))，解得低膨胀微晶玻璃点磨削表面硬度与点磨削参数的模型如式(14)所示，并利用验证实验(表4)对模型进行检验，误差结果如表5所示。

1.2.2 抗胃癌植物类中药 以“中药”“抗肿瘤”等为检索词，在中国知网、维普等数据库中组合查询1980年1月－2018年4月发表的相关文献。纳入抗胃癌植物类中药的相关文献，包括基础/临床研究、综述、个案报道等；排除不在“1.2.1”项下所列品种范围内的相关文献。共检索到抗胃癌植物类中药相关文献478篇，共涉及85个中药品种。

表5　误差表

3.3表面粗糙度Ra单因素数值拟合

图7所示为砂轮速度vc对表面粗糙度Ra的影响，通过考查Ra随vc的变化趋势，经数值拟合，建立起二者之间的数字关系模型，其表达式为

(15)

式(15)模型的决定系数为0.8936。

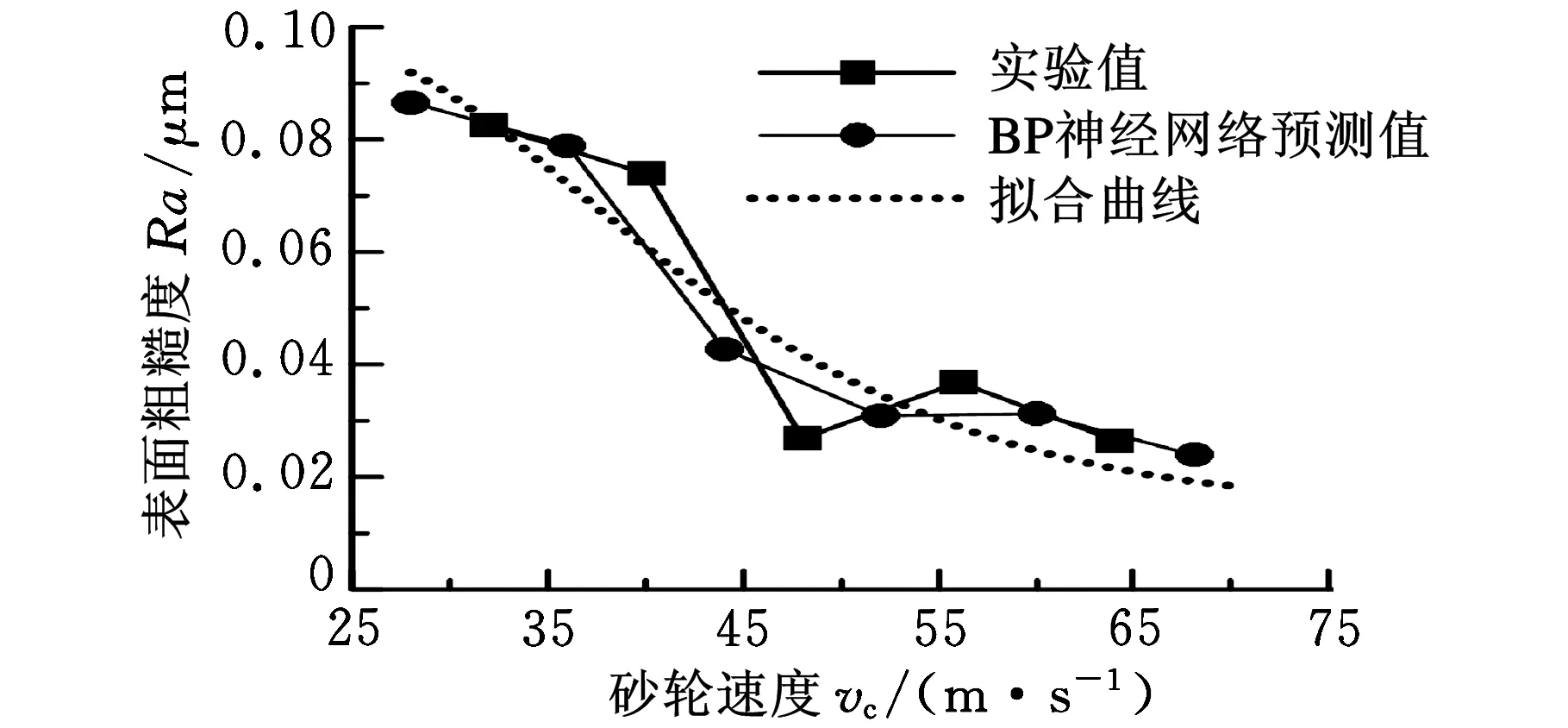
图7　砂轮速度vc对表面粗糙度Ra的影响

同理，经数值拟合，可建立起表面粗糙度Ra与进给率f、磨削深度ap、倾斜角α、偏转角β的模型，其数学表达式分别为

Ra=0.00363f0.819+0.032 61

(16)

(17)

Ra=0.0166αe-0.0472α2+0.0916

(18)

Ra=-0.009 47βe-4.173×10-3β2+0.096 93

(19)

式(16)～式(19)模型的决定系数R分别为0.9462、0.8910、0.8314、0.8700。图8～图11所示分别为f、ap、α、β对表面粗糙度的影响曲线。

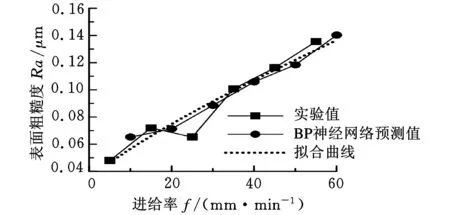
图8　进给率f对表面粗糙度的影响

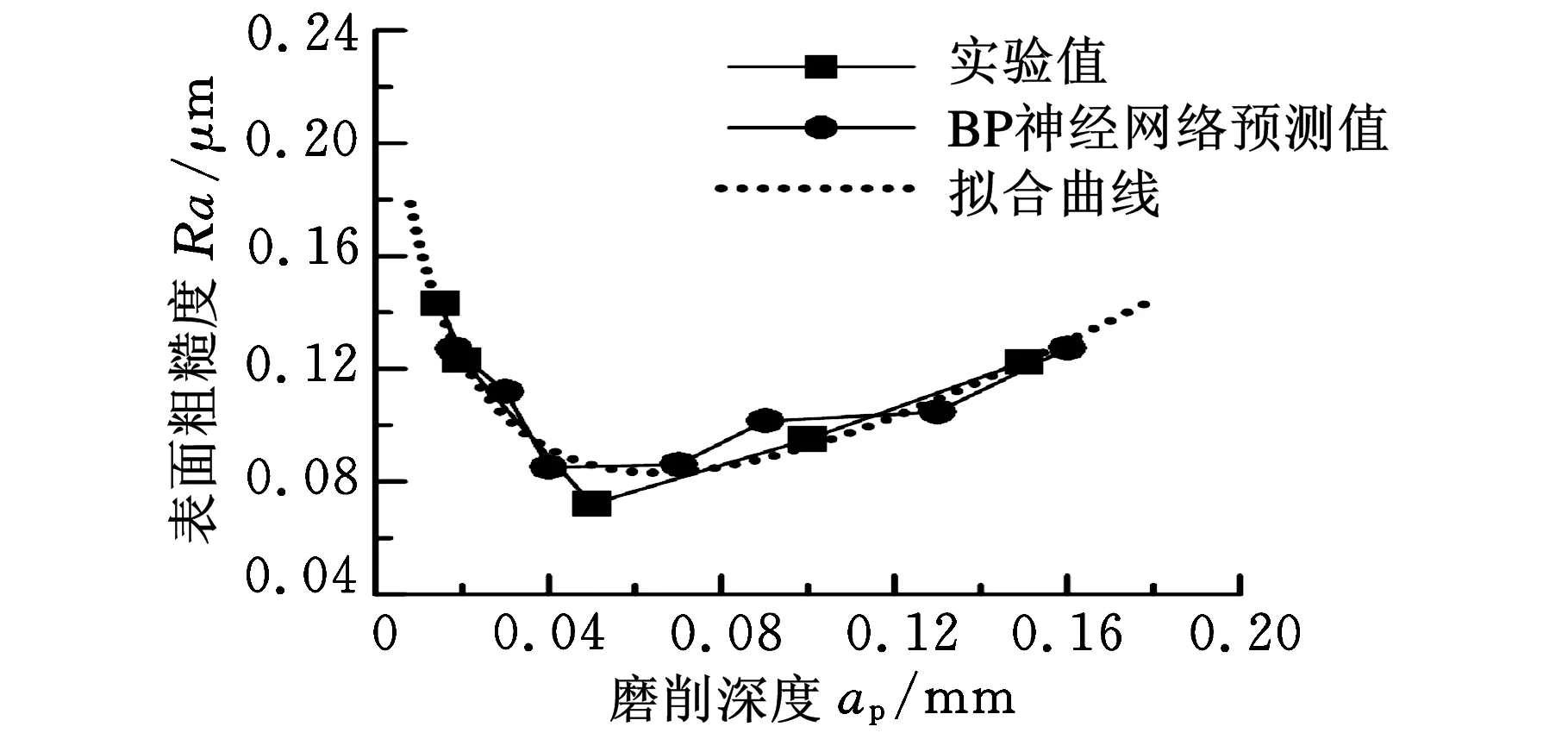
图9　磨削深度ap对表面粗糙度的影响

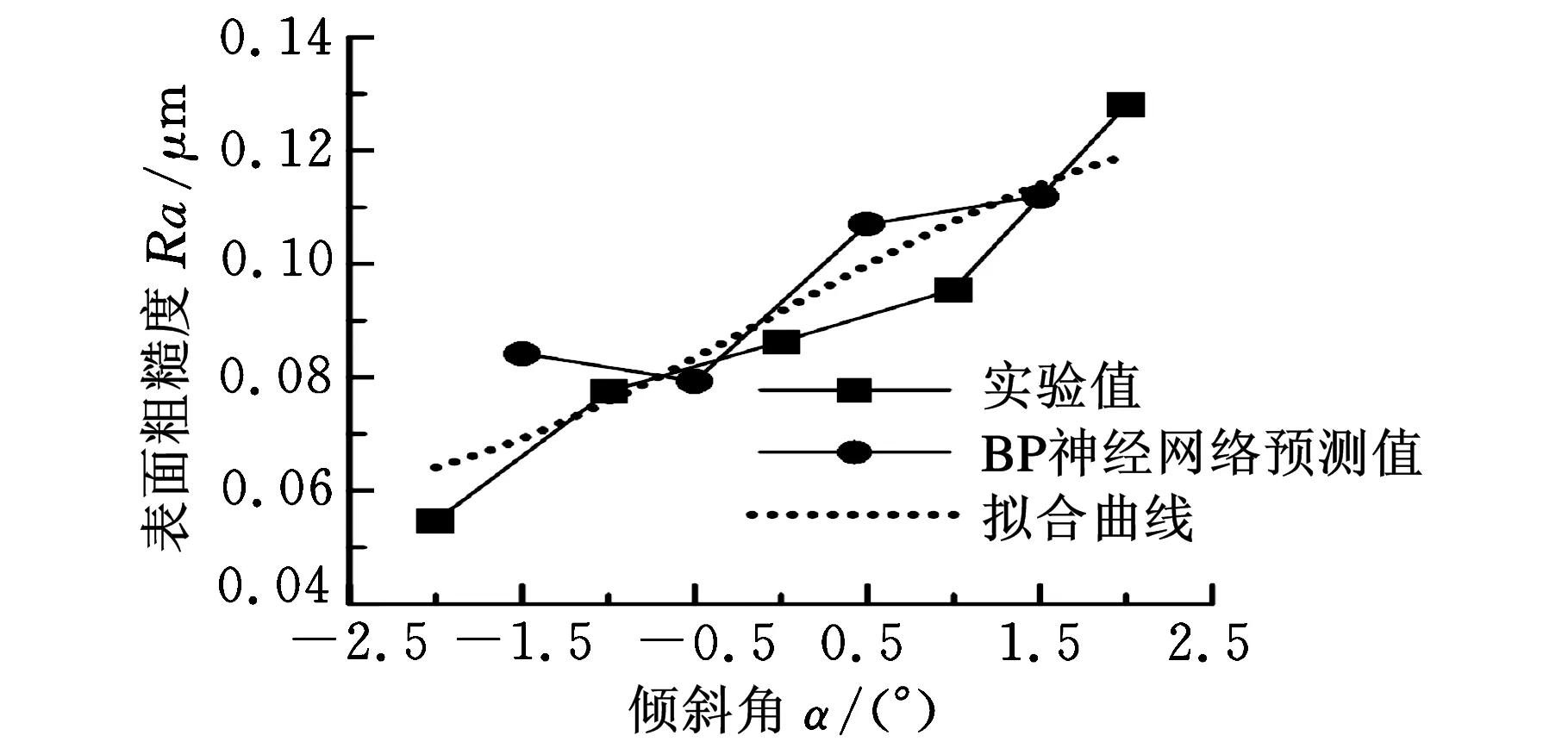
图10　倾斜角α对表面粗糙度的影响

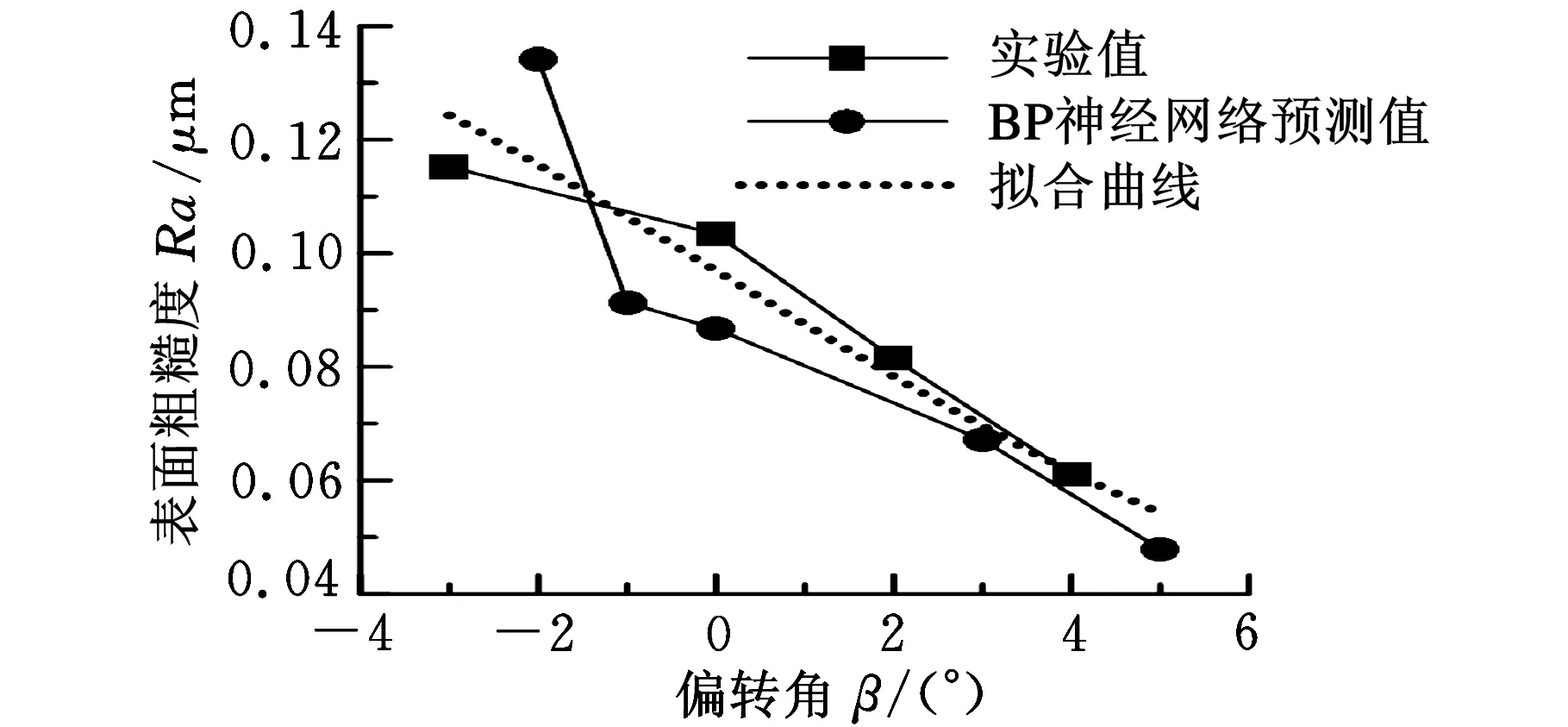
图11　偏转角β对表面粗糙度的影响

3.4表面粗糙度多元模型

3.4.1模型假设

基于单因素数值拟合结果(式(15)～式(19))，建立了点磨削表面粗糙度关于工艺参数的多元模型，其数学表达为

(20)

3.4.2模型求解

模型求解的适应度准则为

(21)

基于正交实验(表2、表3)，建立的遗传算法多元数字模型表达式为

αβe-3.735×10-3vcapα2β2+0.1073

(22)

以多元模型值与正交实验值的方差最小为适应度准则(如式(21))，通过遗传算法对多元模型进行了优化求解，结果如式(22)所示。通过验证实验(表4)检验了多元模型，误差结果如表6所示。

表6　误差表

4　基于遗传算法的双目标优化

4.1目标函数

进行目标函数参数优化的数学表达式及约束条件分别为

W1=max[H(vc,f,ap,α,β)]

(23)

W2=min[Ra(vc,f,ap,α,β)]

(24)

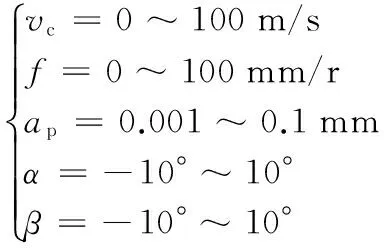
(25)

磨削参数影响加工表面质量，利用遗传算法进行双目标优化，使表面硬度(式(23))取值尽可能大，表面粗糙度(式(24))尽可能小，式(25)为双目标优化的约束条件。

取种群大小为200，进化代数为200，Pareto解因子为0.2，最大进化代数为200，精度为1×10-50。

4.2优化结果

基于遗传算法优化，解得最优工艺参数取值范围:vc为30～31.5m/s，f为20～21mm/min，ap为0.0069～0.0071mm，α为0.495°～0.535°，β为-4.99°～-4.94°，遗传算法Pareto解如图12所示。

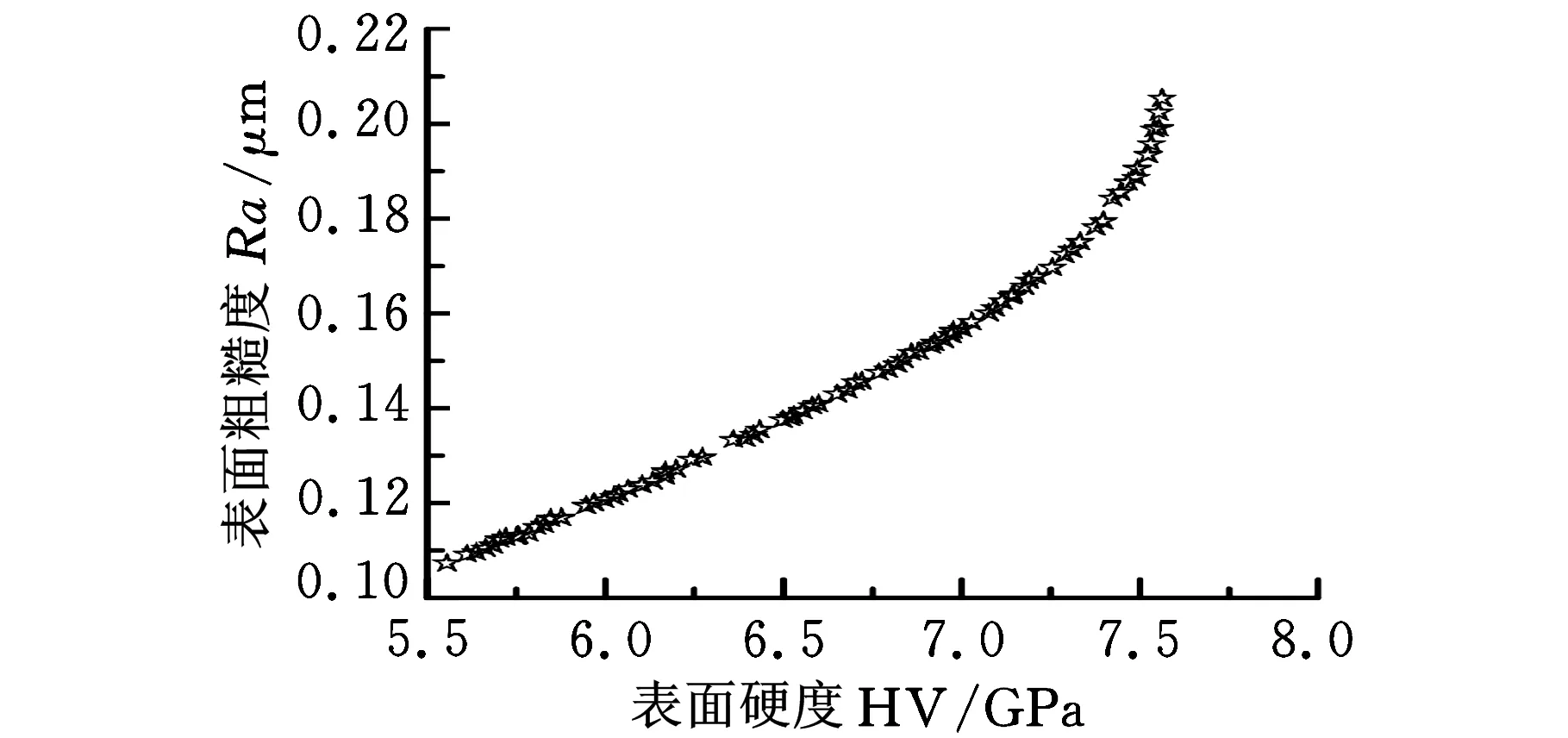
图12　遗传算法Pareto解

在最优工艺参数范围内进行实验验证，取vc=31m/s，f=20.5mm/min，ap=0.007mm，α=0.51°，β=-4.97°，加工后测得的结果为HV=8.641GPa，Ra=0.101μm，与非优化参数实验结果相比，表面硬度明显提高，表面粗糙度略有下降，优化结果较为合理。

5　结论

(1)基于BP神经网络预测值与实验值，通过最小二乘拟合，建立了表面硬度和表面粗糙度分别关于各工艺参数的一元模型，以决定系数检验了模型的可靠度，发现模型具有较高的可靠性。

(2)基于遗传算法，建立了表面硬度和表面粗糙度分别关于工艺参数的多元复合模型，以正交实验进行模型的可靠度验证，结果表明模型具有较高的精度。

(3)基于遗传算法，以表面硬度多元模型和表面粗糙度多元模型为目标函数，进行了工艺参数的双目标优化，得到了一组最优的工艺参数值范围，实验验证结果表明优化结果是合理的。

[1]MaLianjie,GongYadong,ChenXiaohui.StudyonSurfaceRoughnessModelandSurfaceFormingMechanismofCeramicsinQuickPointGrinding[J].InternationalJournalofMachineToolsandManufacture，2014,77:82-92.

[2]修世超, 巩亚东, 蔡光起. 快速点磨削变量角度对表面粗糙度影响机理研究[J]. 中国机械工程, 2008, 19(16): 1895-1897.

XiuShichao,GongYadong,CaiGuangqi.ResearchonMechanismofEffectonSurfaceRoughnesswithPoint-grindingAnglesinQiuck-pointGrinding[J].ChinaMechanicalEngineering, 2008, 19(16): 1895-1897.

[3]巩亚东,仇健,李晓飞,等.超高速点磨削相关机理研究[J]. 机械工程学报, 2010,46(17):172-178.

GongYadong,QiuJian,LiXiaofei,etal.StudyontheCorrelativeMechanismofSuperHigh-speedPointGrinding[J].JournalofMechanicalEngineering,2010,46(17):172-178.

[4]BachH,KrauseD.LowThermalExpansionGlassCeramics[M].Berlin:Springer, 2005.

[5]MustafaEAA.FluorophlogopitePorcelainBasedonTalc-feldsparMixture[J].CeramicsInternational, 2001, 27(1): 9-14.

[6]HollandJH.AdaptationinNaturalandArtificialSystems:anIntroductoryAnalysiswithApplicationstoBiology,Control,andArtificialIntelligence[M].AnnArbor:theUniversityofMichiganPress, 1975.

[7]席裕庚, 柴天佑, 恽为民. 遗传算法综述[J]. 控制理论与应用, 1996, 13(6): 697-708.

XiYugeng,ChaiTianyou,YunWeimin.SurveyonGeneticAlgorithm[J].ControlTheoryandApplications, 1996, 13(6): 697-708.

[8]YuShiwei,ZhuKejun,DiaoFengqin.ADynamicAllParametersAdaptiveBPNeuralNetworksModelandItsApplicationonOilReservoirPrediction[J].AppliedMathematicsandPomputation, 2008, 195(1): 66-75.

[9]吕柏权, 李天铎. 一种具有全局最优的神经网络BP算法[J]. 清华大学学报:自然科学版, 1997, 37(2): 32-34.

LüBaiquan,LiTianduo.BackPropagationAlgorithmofNeuralNetworkwithGlobalOptimization[J].JournalofTsinghuaUniversity:Sci&Tech, 1997, 37(2): 32-34.

(编辑何成根)

Process Parameter Optimization Based on BP Neural Networks and GA in Point Grinding Low Expansion Glass

Ma Lianjie1,2Cao Xiaobing1Gong Yadong2ChenN Xiaohui1

1.Northeastern University at Qinhuangdao,Qinhuangdao,Hebei,066004 2.Northeastern University,Shenyang,110819

The trends of experimental data were analyzed, the surface roughness and surface hardness were tested in point-grinding low expansion glass ceramics. The numerical models of surface roughness and hardness were established by the least square fitting. The accuracy of the model was tested by coefficient of determination, and the model predictions were compared with experimental data to validate the accuracy of the model. The results indicated that the model has high accuracy. Based on BP neural networks and GA, the multivariate numerical models were built on surface roughness and hardness according to the results of orthogonal experiments. And both of the models were selected as the objective function. Optimization goal was the minimum of surface roughness and the maximum surface hardness, dual objectives optimization was carried out based on GA. A range of the optimal solution was obtained about point grinding process parameters. Experimental validation results indicate that optimal results are reasonable.

BP neural network; parameter optimization; point grinding;low expansion glass

2014-08-28

国家自然科学基金资助项目(51275083)

TH161DOI：10.3969/j.issn.1004-132X.2015.01.018

马廉洁，男，1970年生。东北大学秦皇岛分校控制工程学院副院长，东北大学机械工程与自动化学院副教授。主要研究方向为工程陶瓷加工理论与技术。出版专著1部，发表论文70余篇。曹小兵，男，1993年生。东北大学秦皇岛分校控制工程学院本科生。巩亚东，男，1958年生。东北大学机械工程与自动化学院教授、博士研究生导师。陈小辉，女，1982年生。东北大学秦皇岛分校控制工程学院讲师。