基于形态差值滤波和差分熵的滚动轴承故障诊断

姜万录　郑　直　朱　勇　李　扬

1.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，066004

基于形态差值滤波和差分熵的滚动轴承故障诊断

姜万录1,2郑直1,2朱勇1,2李扬1,2

1.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，066004

针对滚动轴承内外圈的早期故障，提出了一种新的诊断方法，该方法融合了数学形态学对非线性信号的滤波和信息熵理论在信号表征方面的优越性。首先，利用数学形态差值滤波器对实测的轴承内外圈轻重损伤的故障信号进行消噪处理，充分突出了有用的故障特征信息；然后，利用差分熵提取该信号中的突变特征信息，对其进行不确定性和复杂性度量；最后，根据突变点的冲击时间间隔和内外圈故障周期性冲击的时间间隔一致的思想来完成对滚动轴承的故障诊断。通过对仿真信号和滚动轴承实测内外圈两种故障程度的振动信号的诊断分析，证明该方法能够很好地识别轴承内外圈早期故障的类型，且具有很高的准确率。

差值滤波器；差分熵；滚动轴承；故障诊断

0　引言

滚动轴承是旋转机械中应用最广的重要部件之一，它对整个旋转机械的工作状态有着重要影响，一旦发生故障可能导致严重后果，因此，滚动轴承的状态监测和故障诊断有着十分重要的意义[1-2]。国内外学者采用自回归模型、神经网络、支持向量机、Hilbert-Huang变换、边际谱等方法成功地对滚动轴承进行了故障诊断[3-5]。

在工程实际中，对滚动轴承进行振动信号采集时会受到严重的噪声干扰，尤其是在故障发生的早期。要获得准确的诊断结果，首先要抑制信号的噪声，使有用的故障特征信息更加突出。形态学滤波是在数学形态学变换的基础上发展起来的一种重要的非线性滤波工具[6-7]，利用该滤波器对信号进行滤波时，能够根据待分析信号的局部形状特征，将其分解为具有物理意义的多个部分，并将其与背景剥离，同时保留信号的主要形状特征[8-9]。目前该方法已成功地应用到对齿轮等故障信号的滤波处理中[10]。

1948年Shannon[11]把热力学中熵的概念引入信息论中，定义了信息熵。信息熵可以定量地描述信息的不确定性和复杂性。目前，信息熵理论已经成功地应用于压缩机气阀、电机和发动机的故障诊断。

本文融合数学形态学滤波的高效消噪能力和信息熵理论在信号表征方面的优越性，提出了一种新的滚动轴承故障诊断方法。

1　数学形态学和差分熵

1.1数学形态学基本变换

数学形态滤波的核心思想是利用起到滤波器作用的结构元素对待分析信号进行形态学迭代运算，从而实现滤波[12]。四种基本的形态学算子分别为腐蚀、膨胀、开和闭。

若f(n)为一维原始离散信号，其定义域为F={0,1,…,N-1}，g(n)为一维离散信号，称其为结构元素，其定义域为G={0,1,…,M-1}，且M≪N，则f(n)关于g(n)的腐蚀和膨胀运算分别定义如下：

(fΘg)(n)=min{f(n+m)-g(m)}

(1)

(f⊕g)(n)=max{f(n-m)+g(m)}

(2)

m∈{0,1,…,M-1}

f(n)关于g(n)的开和闭运算分别定义如下：

(f∘g)(n)=(fΘg⊕g)(n)

(3)

(f•g)(n)=(f⊕gΘg)(n)

(4)

1.2差值滤波器

一维信号f(n)分别经过结构元素g(m)膨胀和腐蚀后的差值称为差值滤波，其表达式为

fDIF(n)=f•g(n)-f∘(n)

(5)

式(5)可以分解为

f•g-f∘g=(f•g-f)+(f-f∘g)

(6)

其中，f•g-f和f-f∘g正是数学形态学中Top-Hat变换中的黑白帽变换，而这两种变换分别能提取信号中的负正脉冲，所以差值滤波器将两种变换融合，能够更好地对信号进行滤波处理，提取信号中的正负脉冲信息，克服了开闭算子在处理实际信号中需要得到正负脉冲的先验知识的缺点[13]。

在本文中，将利用该滤波器对轴承故障信号进行滤波处理。

1.3结构元素

形态学滤波的实质就是通过结构元素与待分析信号进行形态学迭代运算，从而实现滤波目的。所以结构元素的长度对形态学滤波的效果有着重要的影响。

常用的结构元素有扁平型、三角型和半圆型等。三角型和半圆型结构元素具有长度和高度两个参数，分别适用于脉冲噪声和随机噪声的滤除。而只有长度参数的扁平型结构元素具有计算简单、需要优化的参数少等优点，同时因其高度为零，可避免对信号幅值的改变，所以获得了广泛的应用[10]，因此在本文中，选用优化参数少且计算简单的扁平型结构元素来对轴承故障信号进行滤波处理。

1.4差分熵

差分熵(difference entropy，DE)能够凸显信号突变点的信息，设fDIF(n)为滤波器处理后的故障信号，则差分熵的定义如下[14]：

D(n)=fDIF(n+1)-fDIF(n)

(7)

n=0,1,…,N-2

差分熵为

(8)

为减小计算量和提高诊断效率，信号长度L不宜过大。

2　数值仿真算例

2.1仿真信号

为了验证差值滤波器和差分熵两种方法的结合对故障诊断的效果，设计了以下仿真信号进行分析：

x(t)=x1(t)+x2(t)+x3(t)

(9)

其中，x1(t)是频率为16Hz的周期性指数衰减冲击信号，每周期内衰减函数为8e-100tsin(512πt)，周期冲击时间间隔为0.0625s，用来模拟故障冲击信号；x2(t)是周期为20Hz和40Hz的叠加低频谐波干扰信号：cos(40πt)+cos(80πt)；x3(t)为标准差为1的高斯白噪声，用于模拟强背景噪声。采样频率为2048 Hz，采样时间为1 s。

2.2仿真结果分析

图1为模拟故障信号的时域图和0～100 Hz低频段功率谱图。由于高斯白噪声和低频谐波的干扰，从图1a中难以分辨出冲击成分；从图1b中可以清楚地看出20 Hz和40 Hz的低频谐波干扰，而故障频率16 Hz及其倍频处的谱峰已经被背景噪声所淹没。

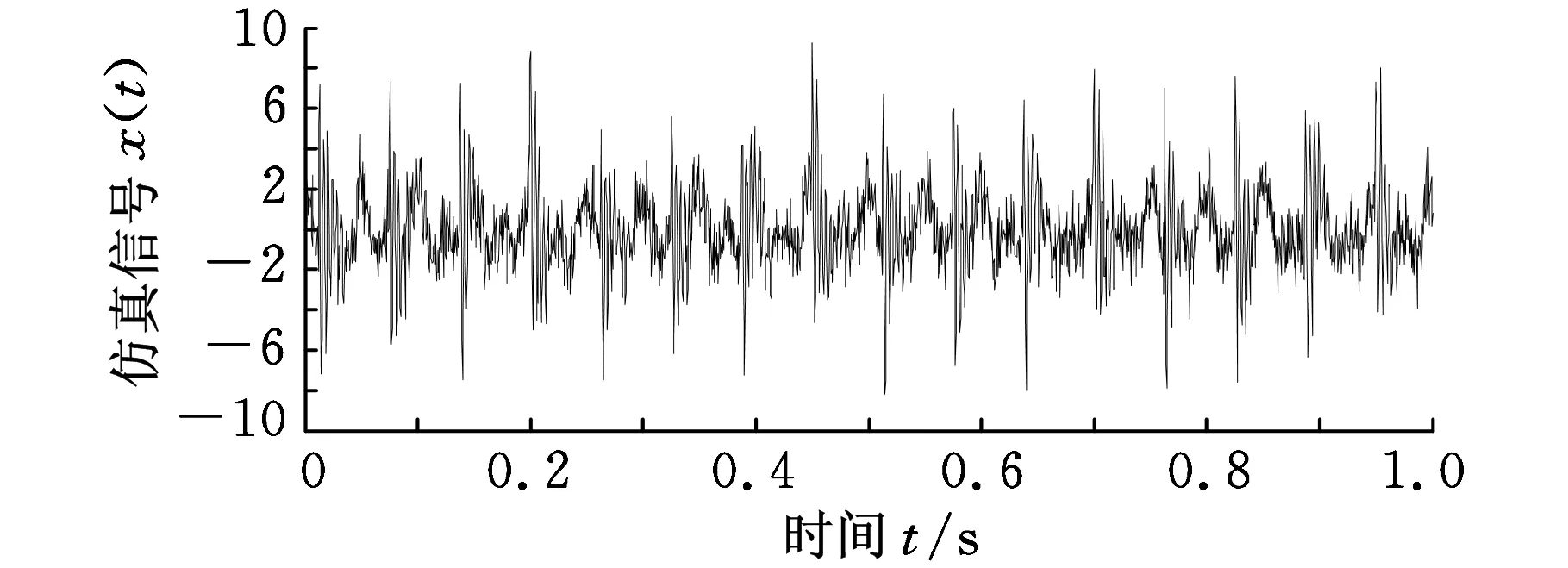
(a)时域图

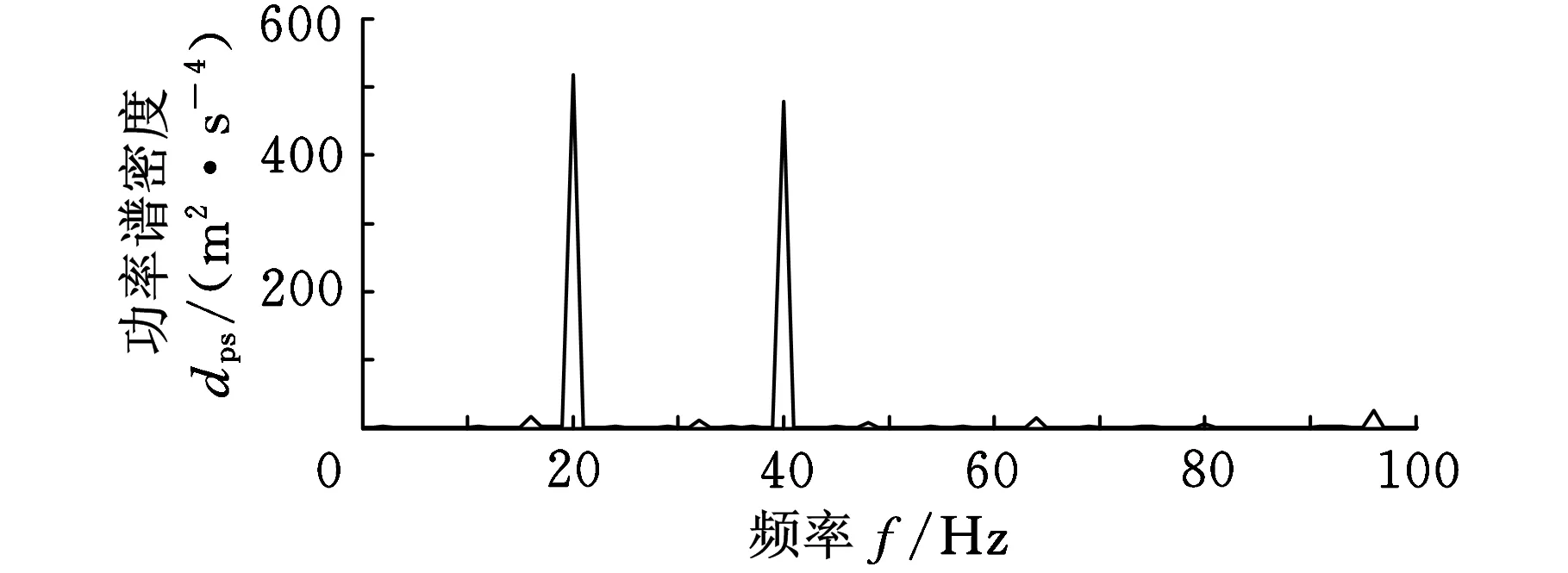
(b)功率谱图图1　含噪声的模拟故障信号

(a)时域图

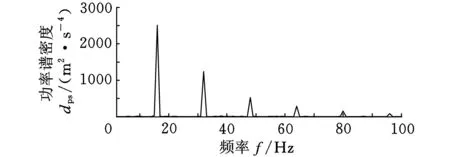
(b)功率谱图图2　滤除噪声的模拟故障信号

为消除噪声的干扰，提高故障诊断的正确率，根据文献[15]提出的滤波最优效果原则：特征频率处的能量占选定频率段的总能量最大时，滤波效果最好。基于这一原则，选取长度为9的扁平型结构元素的差值算子对含有噪声的模拟故障信号进行滤波处理。图2所示为滤波后的结果，图2a展示了清晰可见的冲击成分，图2b展示了故障频率16 Hz及其倍频处的谱峰，峰值也较图1b有很大提高。20 Hz和40 Hz处的低频谐波干扰和高斯白噪声得到了有效的抑制，说明差值滤波器具有很好的滤波效果。

对滤波后的模拟故障信号进行差分熵的求取(L选定为2048)，结果如图3a所示。为了更加准确、高效地进行故障诊断，对差分熵的结果进行了阈值处理，即将小于最大值0.4倍的熵值置为0，如图3b所示。

理论上，在1 s的时间内有16次的冲击，从图3b中可以很明显地看出在1 s时间内有16束熵值线，初步可以诊断出频率为16 Hz的故障。相邻束熵值线间突变平均时间间隔为62.375 ms，和理论周期冲击时间间隔0.0625 s相差0.2%。由此可以看出误差值很小，说明形态差值滤波和差分熵理论的结合可以有效地诊断出该模拟故障。

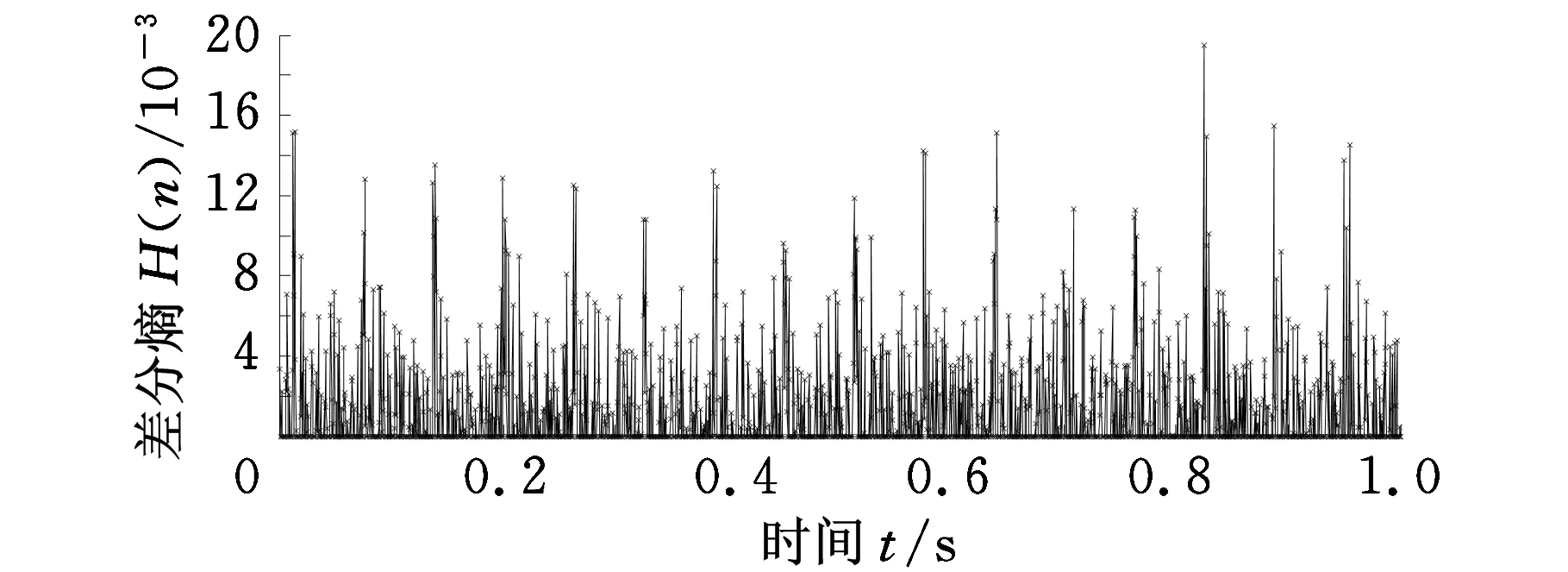
(a)差分熵

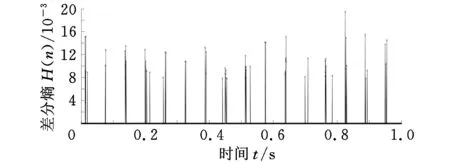
(b)阈值处理后的差分熵图3　仿真信号诊断结果

3　轴承故障信号分析

为了验证该方法的有效性，本文采用美国Case Western Reserve University提供的两种故障程度的滚动轴承内圈和外圈坑点损伤的故障数据，进行进一步实验分析验证[16]。

该轴承的型号为SKF6250，电机转速为1750 r/min，载荷为1.497 kW，转频约为29 Hz。实验中内圈和外圈两处坑点损伤是由电火花机人工加工制作的，轻微故障程度的损伤直径为0.0178 mm，重度故障程度的损伤直径为5.334 mm。内外圈故障的特征频率分别为156 Hz和103.4 Hz[13]。用加速度传感器对电机驱动端进行数据采集，采样频率为12 kHz，采样长度为0.5 s。

3.1轴承内圈故障分析

当滚动轴承出现内圈故障时，故障频率为156 Hz，周期冲击时间间隔为6.41 ms。

滚动轴承具有径向间隙，承受单边载荷，当故障发生时，振动幅值会随着损伤部分与滚动体发生冲击接触位置的不同而发生周期性变化，即发生幅值调制。按轴旋转频率fr进行调制的振动频率为nZfi±fr(n=1,2,…)，以滚动体的公转频率fc进行调制的振动频率为nZfi±fc，其中，Z为滚动体个数，fi为内圈故障频率。

为了更好地显示和观察差分熵故障诊断方法及其优势，截取0.5 s的内圈早期故障信号长度中的0.08 s数据进行分析。图4是长度为0.08 s含有噪声的轴承内圈早期故障信号的时域图和0～1 kHz低频段功率谱图。由于噪声的干扰，从图4a中难以识别冲击成分；图4b展示了在故障频率156 Hz处存在比较模糊的谱峰，但其倍频处的谱峰被噪声淹没，同时在600 Hz处的干扰相对非常大。

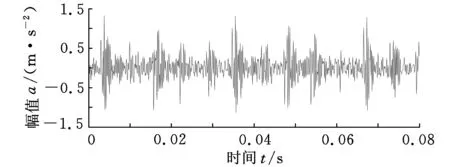
(a)时域图

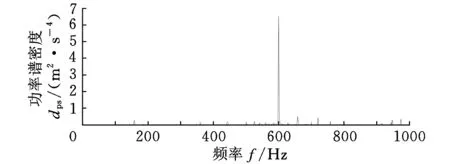
(b)功率谱图图4　轴承内圈轻度损伤含噪声的振动信号

为滤除噪声的干扰，提高故障诊断的准确性，根据文献[15]提出的最优滤波效果原则，选取长度为9的扁平结构元素的差值算子对轴承内圈的早期故障信号进行滤波处理，结果如图5所示。

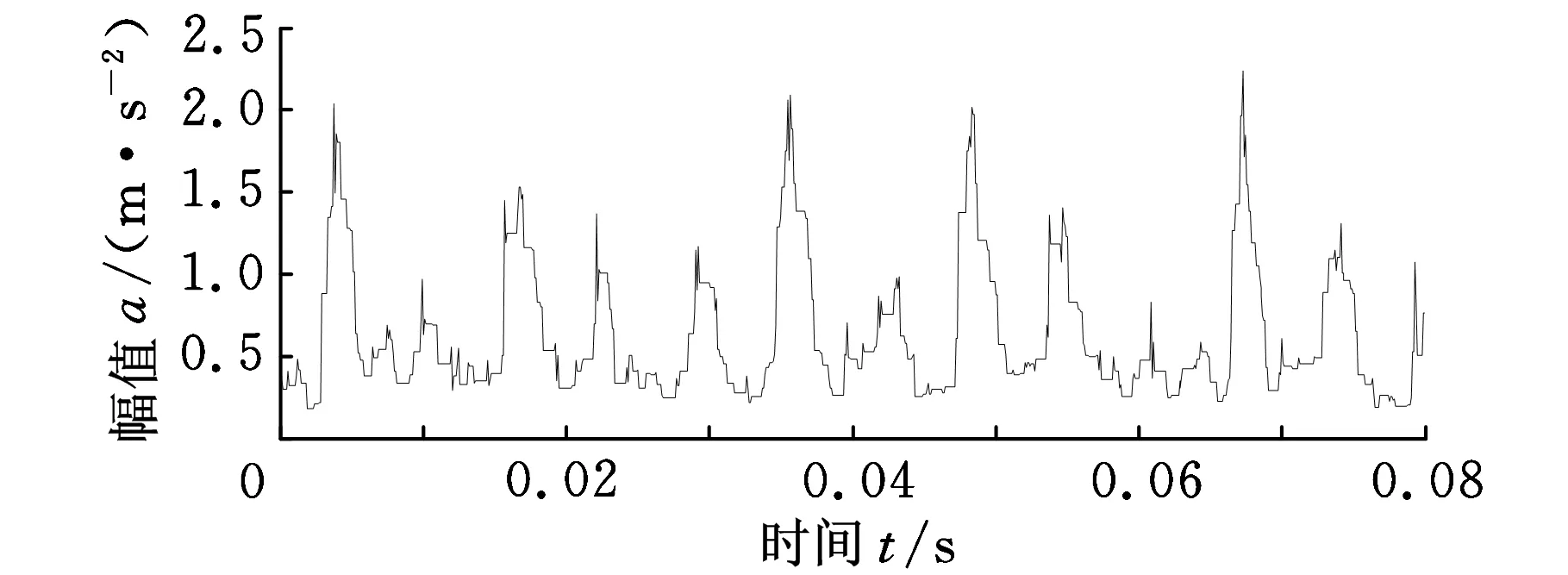
(a)时域图

(b)功率谱图图5　滤波后轴承内圈轻度损伤的振动信号

图5a展示出噪声得到了很好的抑制，冲击成分很明显；图5b展示在故障频率156 Hz及其二倍频处存在谱峰，峰值较图4b有所提高，能够清晰地反映轴承内圈的故障特征，说明差值滤波器对轴承内圈故障信号具有很好的滤波效果。

对滤波后的轴承内圈早期故障信号进行差分熵的求取(L选定为6000)，结果如图6a所示。为了更加准确、有效地进行故障诊断，对差分熵的结果进行阈值处理，即将小于0.4倍最大值的熵值置为0，结果如图6b所示。

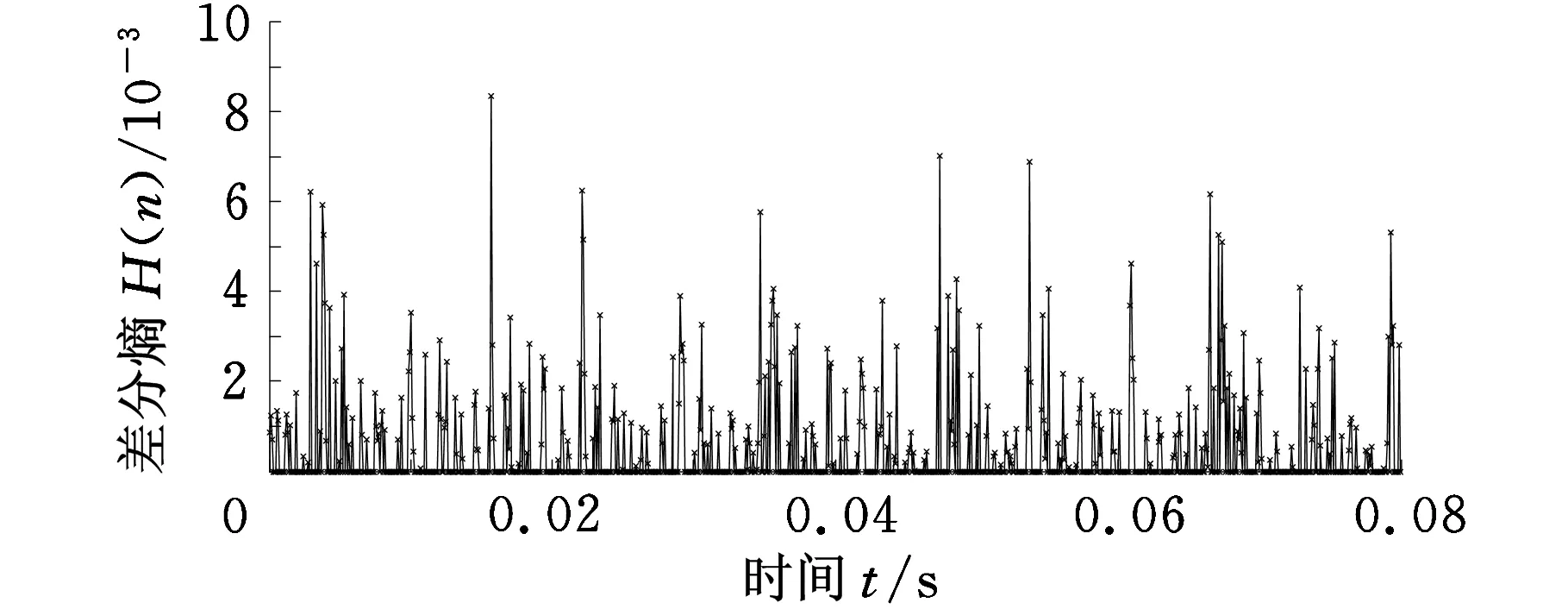
(a)差分熵

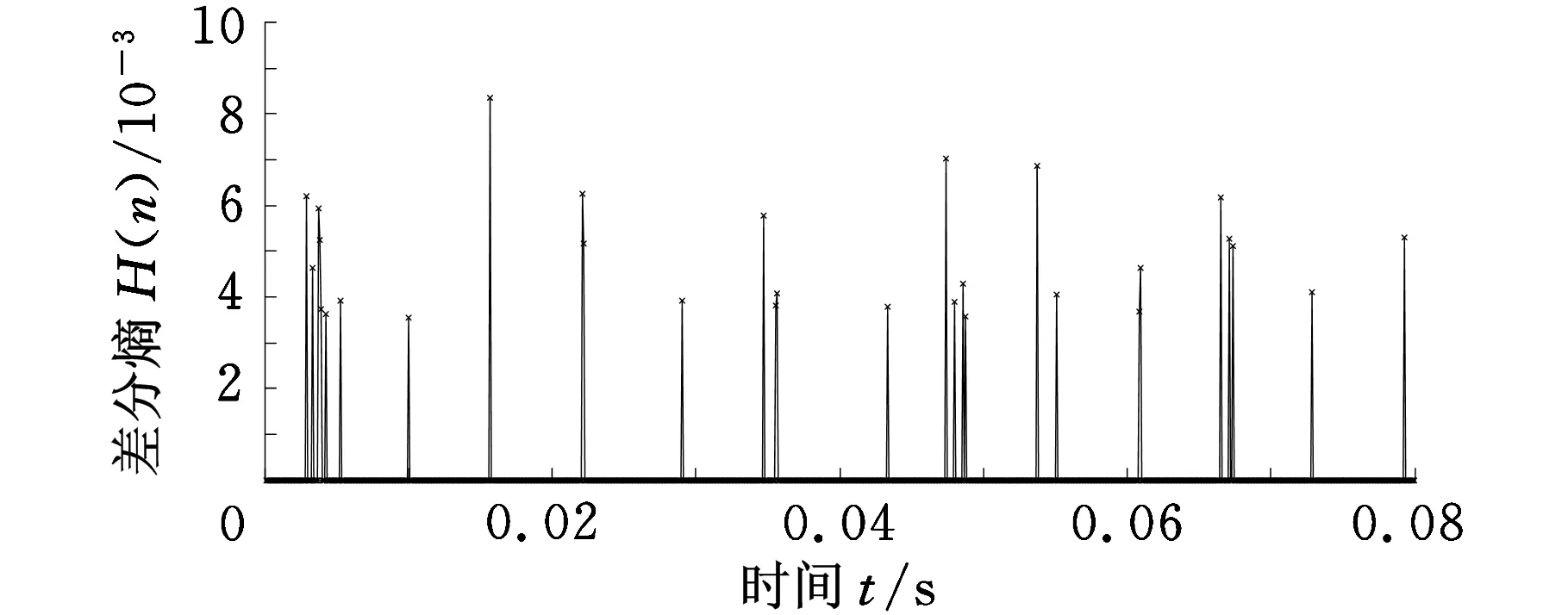
(b)阈值处理后的差分熵图6　轴承内圈轻度故障诊断结果

理论上，在0.08 s时间段内包含12.48次冲击，从图6b中可以很明显地看出在0.08 s时间段内有13束熵值线，所以可判断为轴承内圈故障。突变相邻束熵值线间平均时间间隔为6.2838 ms，和理论周期冲击时间间隔6.41 s相差2.68%。由此可以看出，相邻冲击平均时间间隔误差值非常小，说明形态差值滤波和差分熵理论的结合可以准确地诊断出该故障为轴承内圈的轻度故障。

背景噪声的增强往往伴随着故障程度的劣化，为了考察该方法对轴承内圈重度故障和强背景噪声加大时的有效性，截取0.5 s的轴承内圈重度故障信号长度中的0.08 s的数据进行分析。

图7是长度为0.08 s、含有噪声的轴承内圈重度故障信号的时域图和0～1 kHz低频段功率谱图。图7b展示了在故障频率156 Hz处存在比较模糊的谱峰，其峰值相对很小，其倍频处的谱峰也被噪声淹没，同时在444 Hz和602.5 Hz处的干扰谱峰相对非常大。

(a)时域图

(b)功率谱图图7　轴承内圈重度损伤含噪声的振动信号

为滤除噪声的干扰，提高故障诊断的准确性，根据文献[15]提出的最优滤波效果原则，选取长度为15的扁平结构元素的差值算子对轴承内圈的重度故障信号进行滤波处理，结果如图8所示。

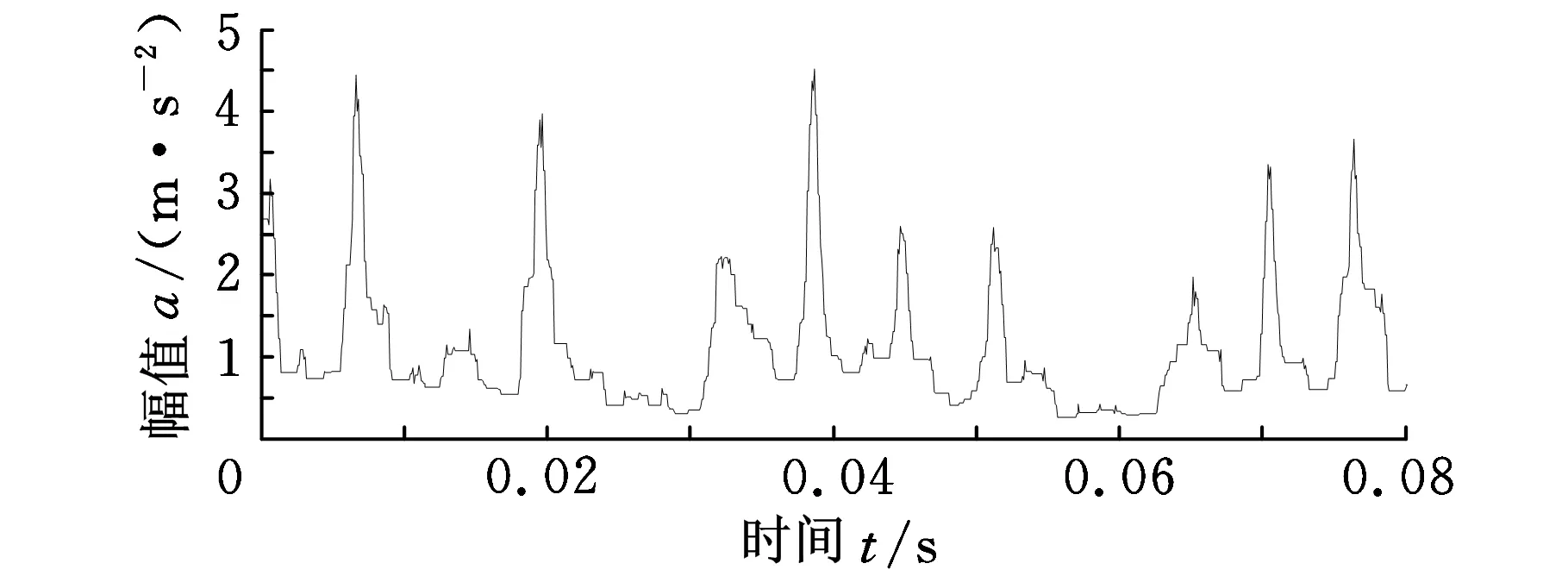
(a)时域图

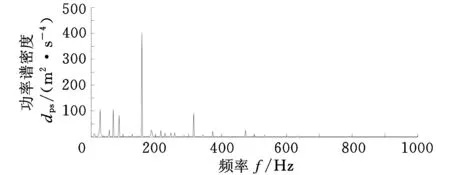
(b)功率谱图图8　滤波后轴承内圈重度损伤的振动信号

对滤波后的轴承内圈重度损伤信号进行差分熵的求取(L选定为6000)，结果如图9a所示。为了更加准确、有效地进行故障诊断，阈值的选取遵循以下原则：相邻束线间的时间间隔能够最大程度地符合轴承内圈故障的理论周期冲击时间间隔，所以将小于0.4倍最大值的熵值置为0，结果如图9b所示。

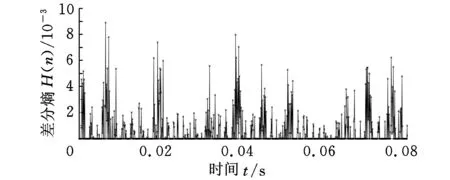
(a)差分熵

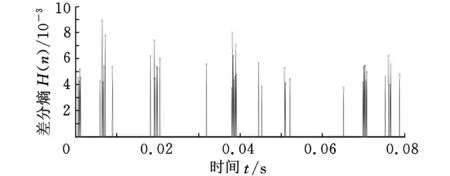
(b)阈值处理后的差分熵图9　轴承内圈重度故障诊断结果

理论上，在0.08 s时间段内包含12.48次冲击，而图9b所展示的有些相邻束线间的时间间隔和理论周期冲击6.41 ms的时间间隔误差不是很大，但是有些时间间隔很不规律，误差也和理论周期冲击的时间间隔相差很大，由此可得：该方法对轴承内圈重度故障的诊断效果不是很理想。

3.2轴承外圈故障分析

当滚动轴承出现外圈故障时，故障频率为103.4 Hz，周期冲击时间间隔为9.671 ms。

当故障发生，在滚动体通过时，会产生冲击振动，由于外圈损伤点以频率Zfo不断产生，所以引起一系列的高频衰减振动，由于阻尼较小，因此脉冲衰减时间比1/(Zfo)要小得多，衰减振动也基本独立，振动频率为Zfo。其中，fo为外圈通过频率。

为了更好地显示和观察差分熵故障诊断方法及其优势，截取0.5 s的外圈早期故障信号长度中的0.08 s数据进行分析。

图10是长度为0.08 s含有噪声的轴承外圈的早期故障信号的时域图和0～1 kHz低频段功率谱图。从图10b可以看出，由于噪声的干扰，在故障频率103.4 Hz及其倍频处的故障特征被噪声淹没，而在故障频率720 Hz处的干扰非常大。

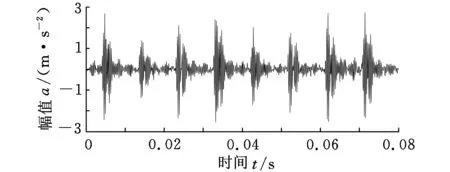
(a)时域图

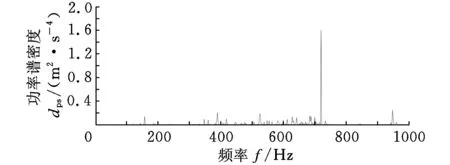
(b)功率谱图图10　轴承外圈轻度损伤的振动信号

为消除噪声的干扰，提高故障诊断的准确性，根据文献[15]提出的最优滤波效果原则，选取长度为5的扁平结构元素的差值算子对轴承外圈早期故障信号进行滤波处理，结果如图11所示。

图11a展示出噪声得到了很好的抑制，冲击成分很明显；图11b中展示在故障频率103.4 Hz及其倍频处存在谱峰，峰值较图10b有很大提高，能够清晰地反映轴承外圈的故障特征，说明差值滤波器对轴承外圈故障信号具有很好的滤波效果。

对滤波后的轴承外圈早期故障信号进行差分熵的求取(L选定为6000)，结果如图12a所示。为了更加准确、有效地进行故障诊断，对差分熵的结果进行了阈值处理，即将小于0.4倍最大值的熵值置为0，结果如图12b所示。

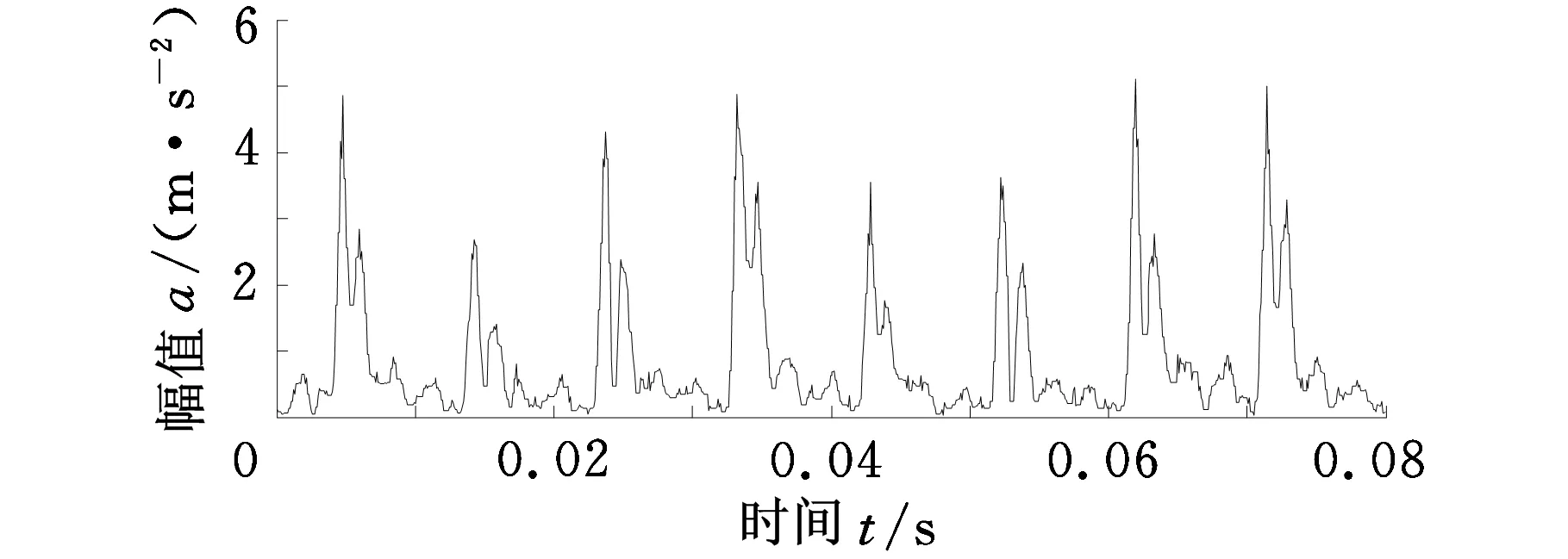
(a)时域图

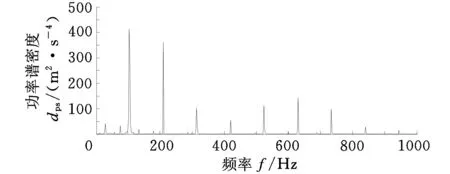
(b)功率谱图图11　滤波后轴承外圈轻度损伤的振动信号

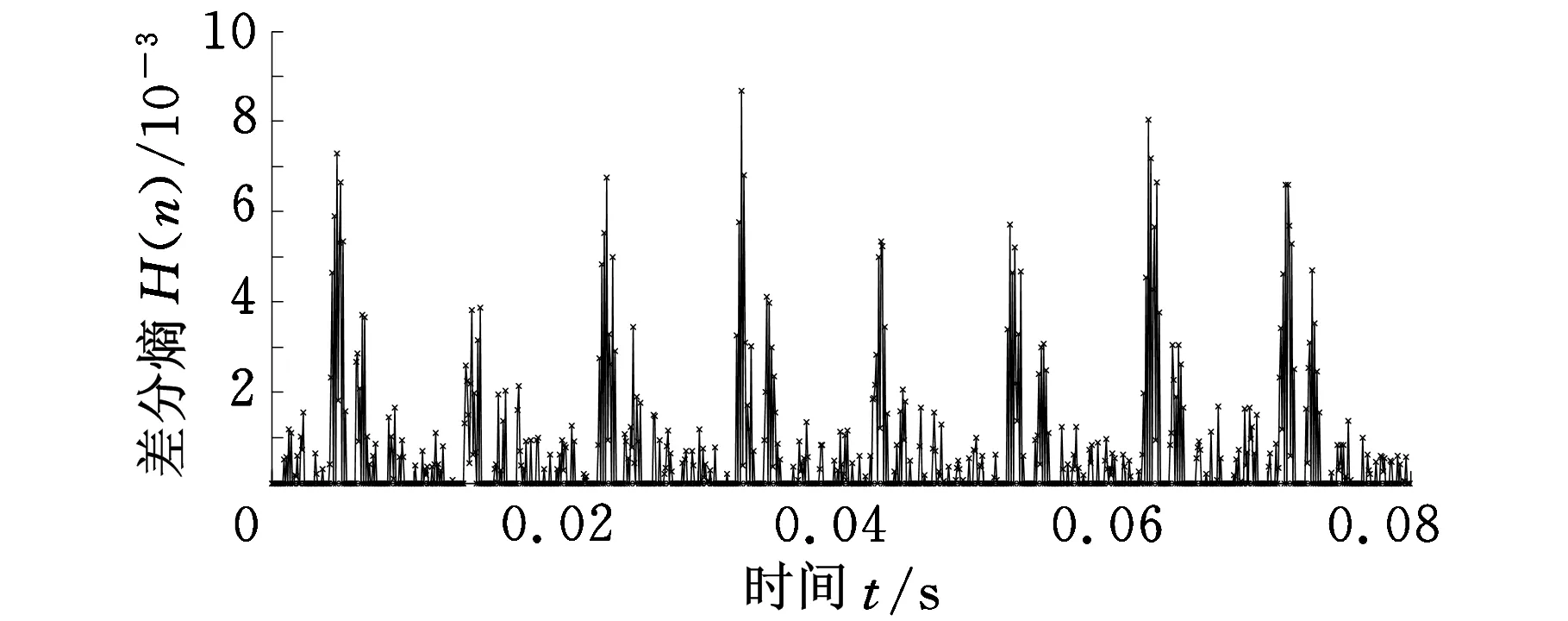
(a)差分熵

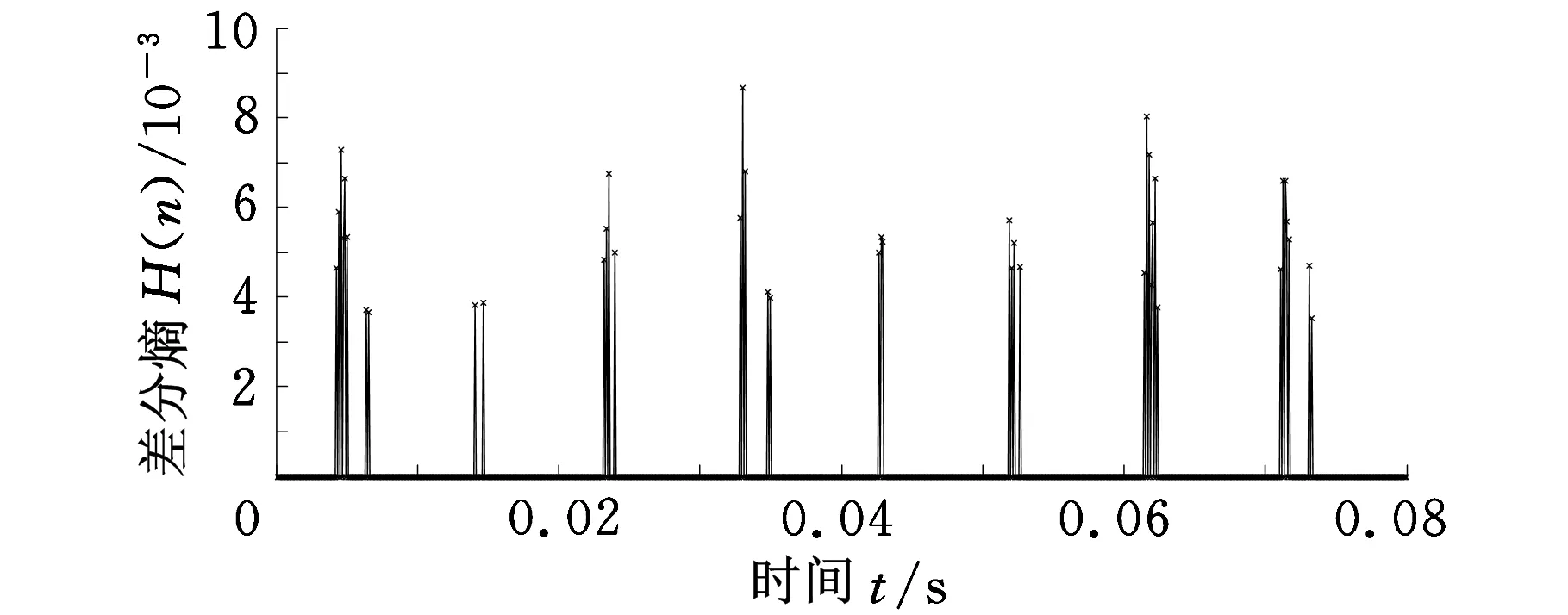
(b)阈值处理后的差分熵图12　轴承外圈轻度故障诊断结果

理论上，在0.08 s时间段内包含8.27次冲击，从图12b中可以很明显地看出在0.08 s时间段内有8束熵值线，所以可判断为轴承外圈故障。相邻束线间突变平均时间间隔为6.299 ms，和理论周期冲击时间间隔相差0.96%。由此可以看出相邻冲击平均时间间隔误差值非常小，说明形态差值滤波和差分熵理论的结合可以准确地诊断出该故障为轴承外圈的轻度故障。

背景噪声的增强往往伴随着故障程度的劣化，为了考察该方法对轴承外圈重度故障和强背景噪声加大时的有效性，截取0.5 s的轴承外圈重度故障信号长度中的0.08 s的数据进行分析。

图13是长度为0.08 s含有噪声的轴承外圈重度故障信号的时域图和0～1 kHz低频段功率谱图。由图13b可以看出，由于噪声的干扰，在故障频率103.4 Hz及其倍频处的故障特征被噪声淹没，并且在故障频率628 Hz处的干扰非常大。

(a)时域图

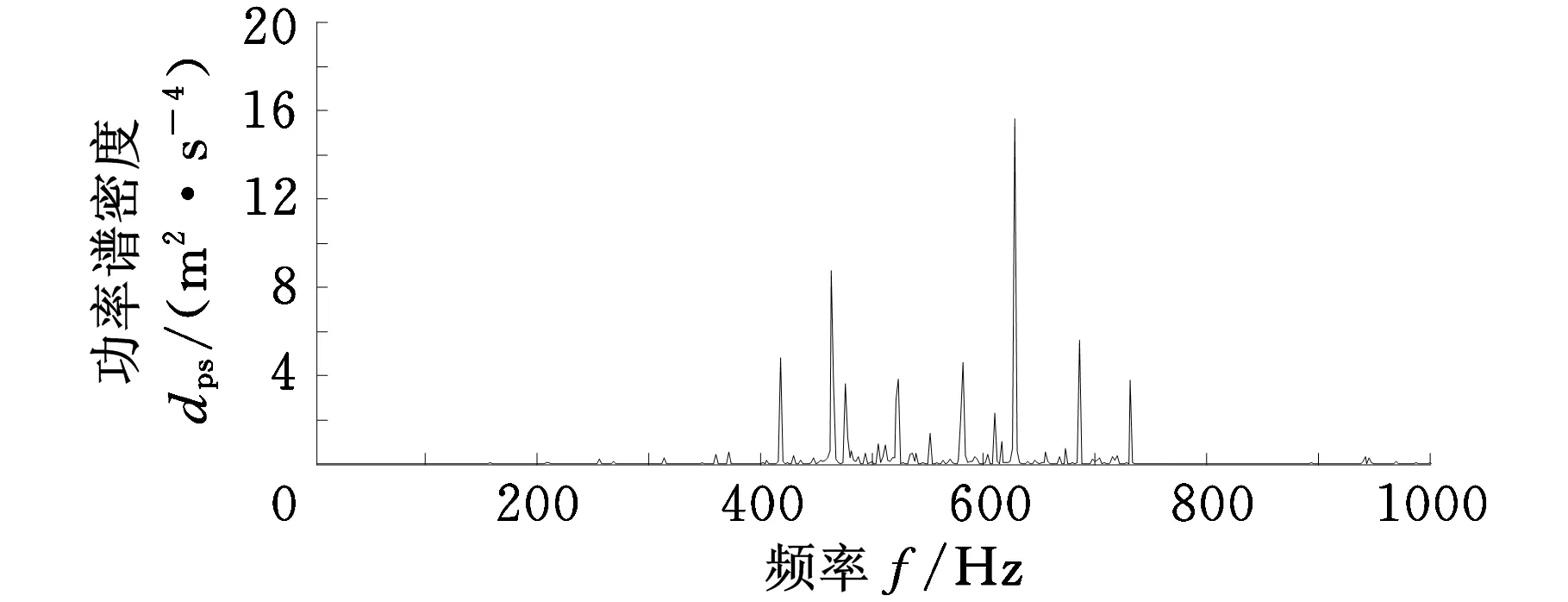
(b)功率谱图图13　轴承外圈重度损伤的振动信号

为消除噪声的干扰，提高故障诊断的准确性，根据文献[15]提出的最优滤波效果原则，选取长度为16的扁平结构元素的差值算子对轴承外圈重度故障信号进行滤波处理，结果如图14所示。

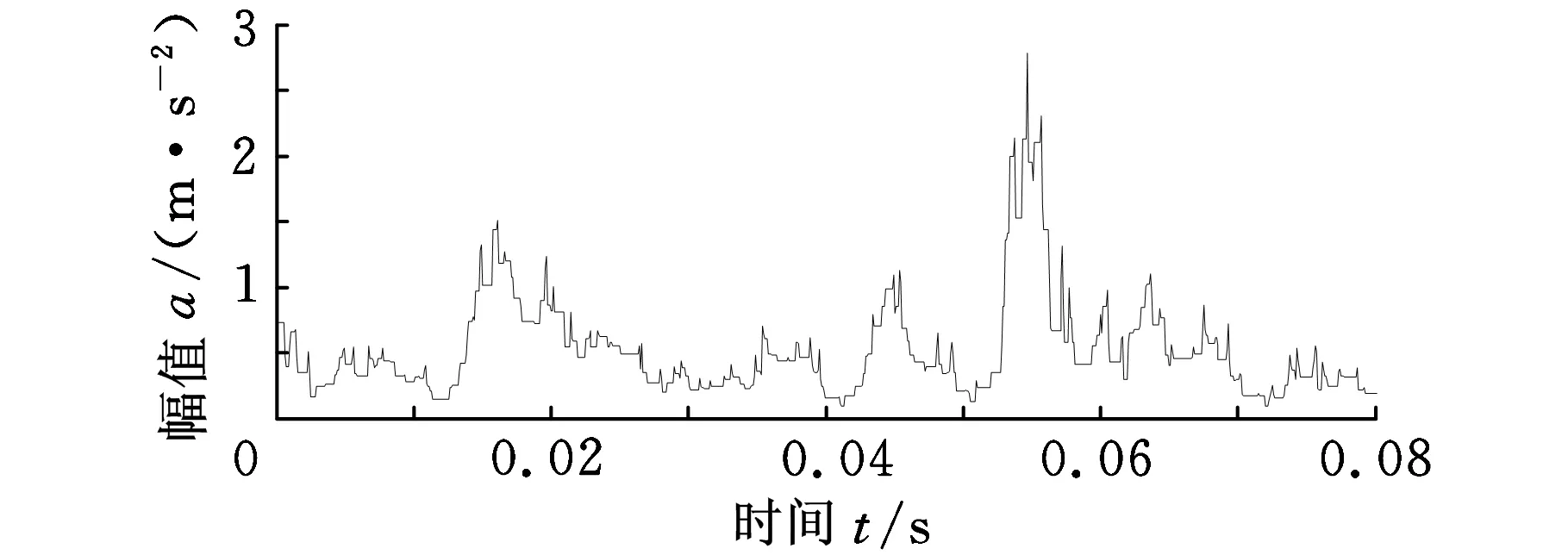
(a)时域图

(b)功率谱图图14　滤波后轴承外圈重度损伤的振动信号

图14a展示出噪声得到了很好的抑制，冲击成分很明显；图14b展示了在故障频率103.4 Hz及其二倍频处存在谱峰，峰值较图13b有很大提高，能够清晰地反映轴承外圈的故障特征，说明差值滤波器对轴承外圈故障信号具有很好的滤波效果。

对滤波后的轴承外圈重度故障信号进行差分熵的求取(L选定为6000)，结果如图15a所示。为了更加准确、有效地进行故障诊断，阈值的选取遵循以下原则：相邻束线间的时间间隔能够最大程度地符合外圈故障的理论周期冲击时间间隔，所以将小于0.25倍最大值的熵值置为0，结果如图15b所示。

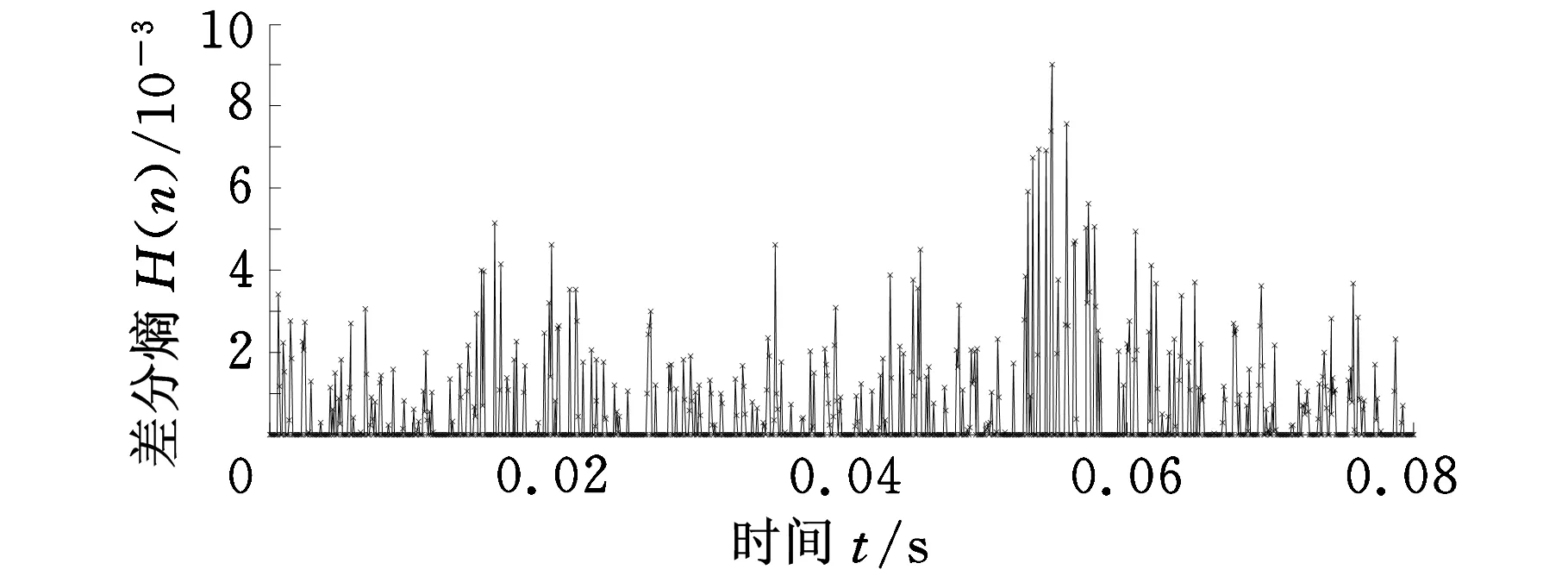
(a)差分熵

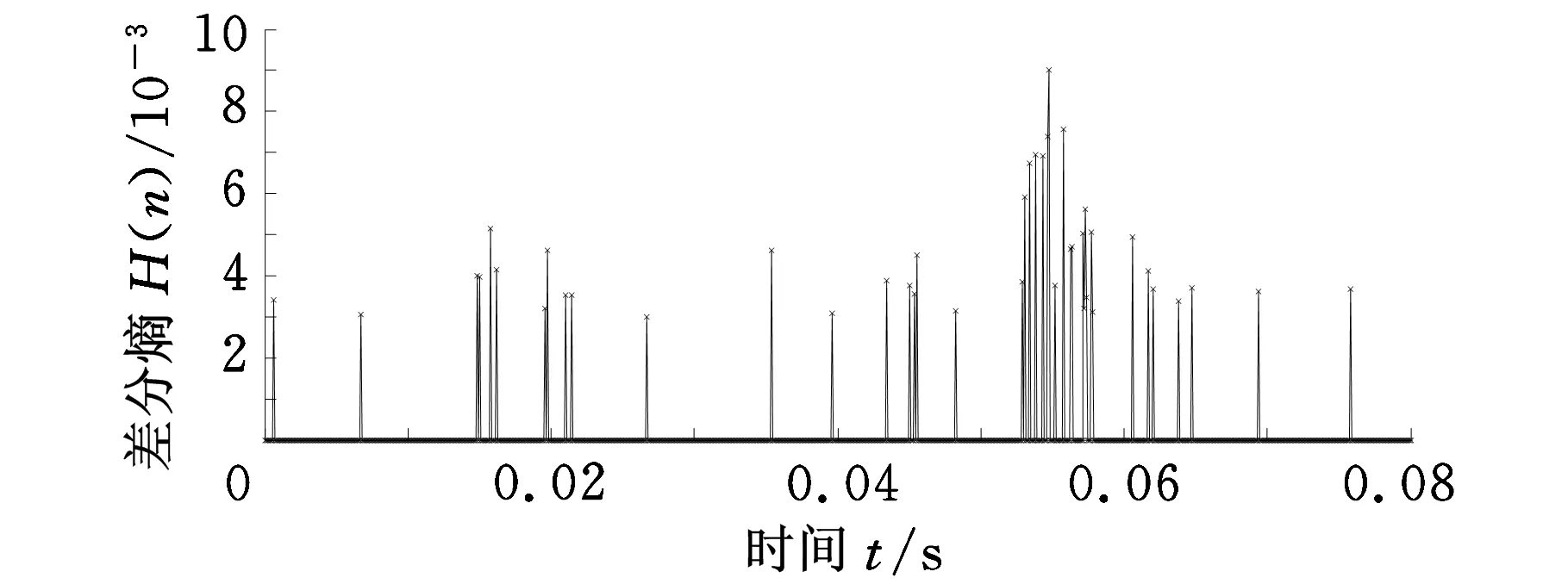
(b)阈值处理后的差分熵图15　轴承外圈重度故障诊断结果

理论上，在0.08 s时间段内包含8.27次冲击，而图15b所展示的相邻束线间的时间间隔很不规律，误差也和理论周期冲击9.671 ms的时间间隔相差很大，由此可得：该方法对轴承外圈重度故障的诊断效果不太理想。

综上所述，本方法较神经网络无需用大量样本对模型进行训练，只需一个样本；较贝叶斯网络无需大量且复杂的先验知识，只需可能出现的故障频率；较支持向量机无需用其他智能方法对参数进行优化，只需简单地设置一个阈值；此外，本方法涉及不到知识冗余，从而避免了降维处理。所以，本方法非常适用于对滚动轴承早期故障的诊断，为早期故障诊断提供了一个很好的工具。其不足之处是对晚期故障(即伴随着强噪声背景的重度故障)的诊断效果不是很理想，有待进一步深入研究。

4　结论

(1)形态差值滤波器能够很好地滤除轴承内外圈故障信号的噪声，提取出更多的有用故障特征信息。

(2)差分熵算法能够很好地根据故障信号突变点的时间间隔和特定故障周期性冲击的时间间隔一致的思想来高效、准确地对滚动轴承进行早期的故障诊断，且具有很高的准确率。

[1]Wang Huaqing，Chen Peng. Intelligent Diagnosis Method for Rolling Element Bearing Faults Using Possibility Theory and Neural Network[J]. Computer & Industrial Engineering, 2011, 60(4): 511-518.

[2]Widodo A, Kimb E Y, Sonc Jong-Duk,et al. Fault Diagnosis of Low Speed Bearinging Based on Relevance Vector Machine and Support Vector Machine[J]. Expert Systems with Applications,2009, 36(3): 7252-7261.

[3]Wang Chun-Chieh, Kang Yuan, Shen Ping-Chen,et al. Application of Fault Diagnosis in Rotating Machinery by Using Time Series Analysis with Neural Network[J]. Expert Systems with Applications, 2010, 37(2): 1696-1702.

[4]Kankar P K，Sharma S C, Harsha S P. Fault Diagnosis of Ball Bearinging Using Machine Learning Methods[J]. Expert Systems with Applications, 2011, 38(3): 1876-1886.

[5]Li Hui， Zhang Yuping, Zheng Haiqi. Hilbert-Huang Transform and Marginal Spectrum for Detection and Diagnosis of Localized Defects in Roller Bearings[J]. Journal of Mechanical Science and Technology, 2009, 23(2): 291-301.

[6]Serra J. Image Analysis and Mathematical Morphology. Vol.1[M]. New York: Academic Press, 1982.

[7]Serra J.Image Analysis and Mathematical Morphology.Vol.2: Theoretical Advances[M].New York: Academic Press, 1988.

[8]Matagos P，Schafer R W. Morphological Filters-Part I: Their Set-theoretic Analysis and Relations to Liner Shift-invariant Filters[J].IEEE Transactions on Acoustics, Speech and Signal Processing, 2008, 22(3): 597-610.

[9]Matagos P，Schafer R W. Morphological Filters-Part II: Their Relations to Median, Order-statistic and Stack Filters[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 2008, 22(3): 1170-1184.

[10]Li Bing,Zhang Peilin.Gear Fault Detection Using Multi-scale Morphological Filters[J].Measurement,2011,44(10):2078-2089.

[11]Shannon C E. A Mathematical Theory of Communication[J]. The Bell System Technical Journal,1984,27:597-610, 623-656.

[12]Dong Yabin,Liao Mingfu,Zhang Xiaolong, et al.Fault Diagnosis of Rolling Element Bearinging Based on Modified Morphological Method[J]. Mechanical Systems and Signal Processing, 2011, 25(4): 1276-1286.

[13]Zhang Lijun， Xu Jinwu, Yang Jianhong, et al. Multiscale Morphology Analysis and Its Application to Fault Diagnosis[J]. Mechanical Systems and Signal Processing, 2008, 22(3): 597-610.

[14]赵静，何正友，钱清泉. 利用广义形态滤波与差分熵的电能质量扰动检测[J].中国电机工程学报,2009, 29(7): 121-127.

Zhao Jing, He Zhengyou, Qian Qingquan. Detection of Power Quality Distribution Utilizing Generalized Morphological Filter and Difference-entropy[J].Proceeding of the CSEE, 2009, 29(7): 121-127.

[15]沈路，周晓军，张文斌，等. 形态解调在齿轮故障特征提取中的应用[J].浙江大学学报(工学版), 2010,44(8): 1514-1519.

Shen Lu, Zhou Xiaojun, Zhang Wenbin,et al. Application of Morphological Demodulation in Gear Fault Feature Extraction[J]. Journal of Zhejiang University(Engineering Science), 2010, 44(8): 1514-1519.

[16]Loparo K A.Bearing Vibration Data Set, Case Western Reserve University[EB/OL].http://csegroups.case.Edu/bearinging data center/home.

(编辑陈勇)

Fault Diagnosis of Rolling Bearings Based on Morphological Difference Filter and Difference Entropy

Jiang Wanlu1,2Zheng Zhi1,2Zhu Yong1,2Li Yang1,2

1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University,Qinhuangdao，Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science (Yanshan University),Ministry of Education of China,Qinhuangdao，Hebei,066004

Concerning the early fault diagnosis of inner and outer race, a novel method was proposed. The method put the advantages of mathematical morphology filtering nonlinear signals and the advantages of information entropy theory characterizing signals together. Firstly, the measured slight and severe fault signals of inner and outer race faults were filtered by morphological difference filter to get more useful fault characteristic informations. Secondly, the abrupt informations of signals were extracted by difference entropy, and the uncertainty and complexity of abrupt information were measured by difference entropy. Lastly, the faults were diagnosed successfully based on the mind of the periodic time interval of abrupt point coincided with the periodic impulsive time interval of inner and outer race faults. The simulation signals and the two fault signals of the rolling bearing were tested and verified, the result is that the new method can diagnosis the early faults of inner and outer race with high accuracy.

difference filter; difference entropy; rolling bearing;fault diagnosis

2013-07-30

国家自然科学基金资助项目(51475405)；国家重点基础研究发展计划(973计划)资助项目(2014CB046405)；河北省自然科学基金资助项目(E2013203161)

TH137；TP277< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.01.011

姜万录，男，1964年生。燕山大学机械工程学院教授、博士研究生导师。主要研究方向为现代检测技术与信号处理、控制理论与控制工程、故障诊断与智能信息处理、冷轧工艺及厚度控制。获国家科技进步二等奖2项，省部级科研奖励7项。出版专著2部，发表论文180余篇。郑直(通信作者)，男，1985年生。燕山大学机械工程学院博士研究生。朱勇，男，1986年生。燕山大学机械工程学院博士研究生。李扬，男，1986年生。燕山大学机械工程学院硕士研究生。