轴承内圈与轴的配合过盈量分析

尤绍军，张晶

(瓦房店轴承集团有限责任公司，辽宁 瓦房店 116300)

符号说明

B——轴与内圈接触区宽度，mm

d——装配前轴承内径，mm

d′——装配后轴承实际内径，mm

d1——装配前轴的直径，mm

d2——装配后轴的实际直径，mm

E1——内圈的弹性模量，MPa

E2——轴的弹性模量，MPa

F——装配后内圈受到的周向张力，N

F1——轴与内圈过盈配合产生的静摩擦力，N

F2——轴带动内圈旋转的摩擦力，N

H1——装配前内圈壁厚，mm

H2——装配后内圈壁厚，mm

L——过盈装配后内圈滚道周向胀大量，mm

M——轴带动内圈转动的力矩，N·mm

P——内圈作用在轴上的压力，N

δ1——装配后轴的表面压应力，MPa

δ2——装配后内圈受到的周向张应力，MPa

μ——内圈与轴之间的摩擦系数

ν——泊松比

在机械系统中，轴承内圈与轴一般采取过盈配合，该过盈配合影响着轴承的工作游隙，进而间接影响着轴承的工作性能，因此，轴承内圈和轴的过盈量是否恰当，显得尤为重要。现对轴承内圈和轴的配合过盈量进行探讨分析。

1 有关参数的计算

轴承内圈与轴过盈配合的过盈量较小，因此，文中的计算仅考虑弹性变形。

由于内圈与轴为过盈配合，因此

d2=d′。

(1)

内圈在轴的表面产生的压应力δ1为

(2)

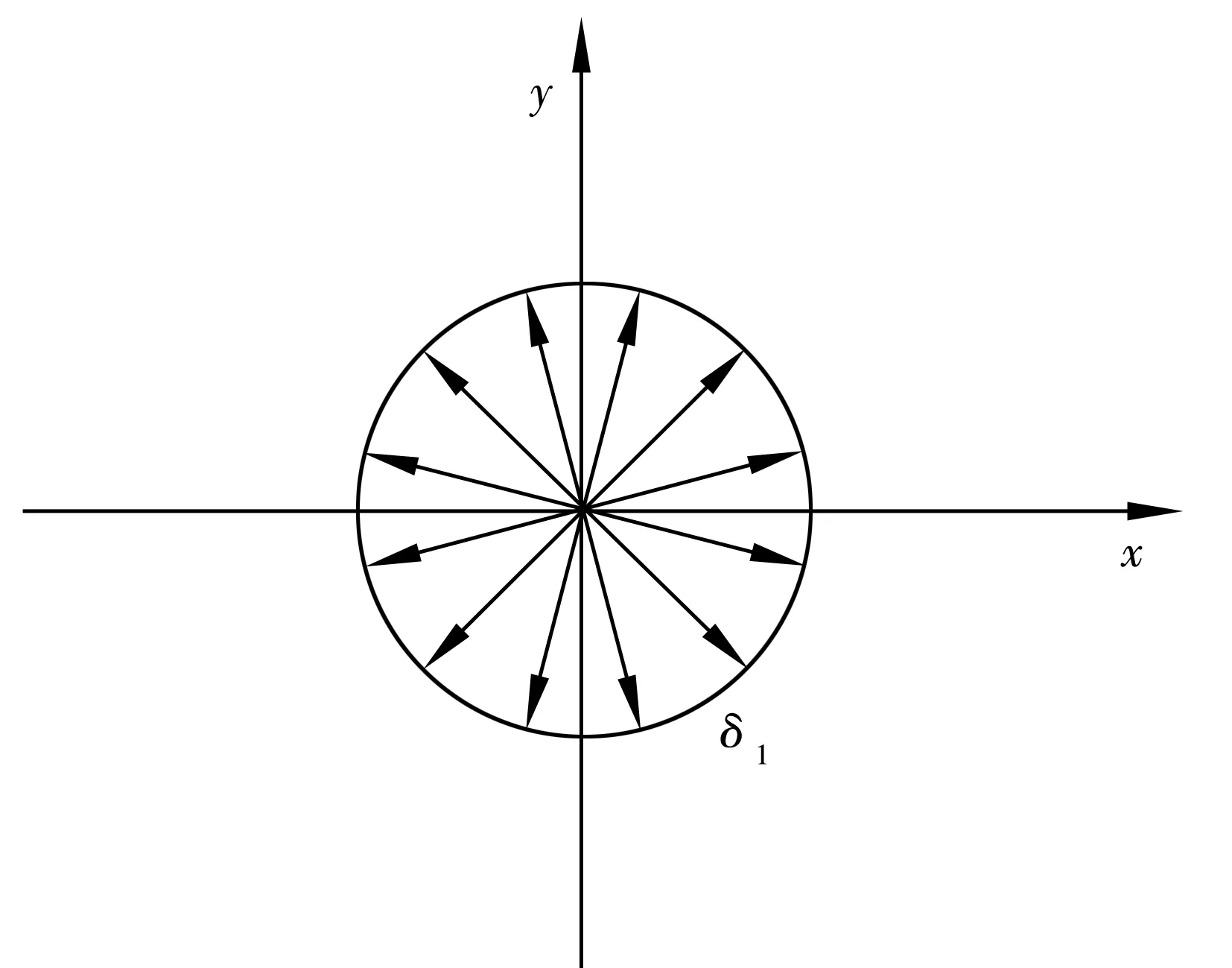
图1 内圈与轴过盈配合后内圈受到的周向张力示意图

(3)

内圈的1/4圆上受到的径向张力在y轴方向的分量之和为

(4)

设θ=i/n，则dθ=1/n，

(5)

(6)

装配后内圈受到的周向张应力δ2为

(7)

(8)

则由(7)和(8)式得

(9)

装配后内圈壁厚H2为

(10)

内圈作用在轴上的压力为

(11)

轴与内圈过盈配合产生的的静摩擦力F1为

(12)

过盈装配后内圈滚道胀大量为

轴在运转过程中带动内圈转动的力矩M为已知值，等于轴承转动的摩擦力矩，可以通过测量获得，也可以通过轴承转动过程中的功耗计算求得。轴通过与内圈过盈配合带动内圈转动所需的摩擦力为

(14)

2 理论公式的应用

2.1 轴与内圈配合过盈量的优化

为了防止轴与内圈间产生滑动，带动内圈转动的摩擦力F2必须小于轴与内圈间的静摩擦力F1。但是，轴与内圈间的过盈量并非越大越好，过盈量过大，必然使轴产生过大的压应力，从而在接触区与非接触区之间的过渡区域产生极大的拉应力，显著降低轴的弯曲和扭转疲劳强度。同时，内圈产生大的张力与其高速旋转产生的离心力叠加，易导致断裂；而且，该力也使内圈滚道产生拉应力，降低了内圈的疲劳强度。因此，在保证F1>F2，并有一定的安全系数下，过盈量应越低越好。利用上述公式及此处的约束条件，可以对内圈与轴的过盈量进行优化。

2.2 内圈滚道胀大量计算

轴与内圈过盈装配后,内圈滚道必然胀大，从而影响轴承的游隙，为了保证轴承的正常工作，选择轴承游隙时必须考虑过盈装配对游隙的影响。对一些内圈壁厚变化较大的轴承，内圈滚道胀大量不一致必然导致轴承接触角的改变，这对一些薄壁轴承、内径带锥度的轴承、小游隙的精密轴承尤为重要。例如角接触球轴承与机床主轴配合时，即为通过调整轴与内圈间的过盈量来调整轴承的游隙和接触角。

因此，轴与轴承装配时，通过计算确定内圈滚道胀大量，并据此确定轴承装配前的游隙和接触角，确保轴承装配后的游隙和接触角符合要求，是一件非常重要的工作。通过(9)和(13)式，可以准确地计算出轴承内圈任何部位的胀大量。

2.3 轴与轴承性能的影响分析

通过(2)，(7)，(9)式可以计算出轴与内圈过盈配合后轴与轴承内部的应力，从而评估出轴与内圈过盈配合对轴与轴承性能的影响。也可以通过实测轴与内圈过盈装配后内圈滚道胀大量，并把D1作为已知值，通过(9)和(13)式计算出d1的值，并将其与d1的测量值比较，差值作为过盈量修正值。

3 结束语

通过对轴承内圈与轴间过盈时产生的作用力与尺寸变化的分析，推导出了计算轴承内圈与轴间作用力和尺寸变化的一系列公式，这些公式可以帮助设计者优化轴与内圈配合过盈量，计算内圈滚道胀大量以及评估过盈配合对轴与轴承性能的影响。