椭圆超声功率切削驱动装置中的优化BUCK模型

陈明方　邹　平　何　宇　吴　昊　张永霞

1.东北大学，沈阳，110819　　2.沈阳职业技术学院，沈阳，1100453.辽沈工业集团有限公司，沈阳，110045

椭圆超声功率切削驱动装置中的优化BUCK模型

陈明方1,2邹平1何宇1吴昊1张永霞3

1.东北大学，沈阳，1108192.沈阳职业技术学院，沈阳，1100453.辽沈工业集团有限公司，沈阳，110045

针对椭圆超声功率切削驱动装置的BUCK变换器模型进行优化研究，充分考虑变换器中各元器件的寄生参数对模型的影响，同时对其中LC优化设计进行了较为深入的分析，设计出优化的变换器模型并制作出其对应的验证电路。对该模型中的两个重要传递函数模型的BODE图进行了试验与仿真对比分析，结果证明该模型比较理想地反映了真实电路的动态性能，较好地指导了变换器的设计。

超声功率切削驱动装置；椭圆振型；BUCK变换器；模型

0　引言

超声振动辅助切削技术最近又重新引起学术界的关注，并再一次成为关注的热点。其中，在旋转超声切削方面，讨论更多的是二维超声振动辅助切削技术。根据刀具安装机构与换能器之间是否谐振，二维超声切削分为谐振型和功率型两种。谐振型的机械和电气驱动结构相对简单，刀架体积小，制作工艺流程少，成本较低。但该类型的振型控制困难，振型驱动的控制理论要求高，制作及安装工艺要求高。上述因素直接影响加工质量和加工效果[1-2]。功率型的机械机构设计复杂，刀架体积大，电气驱动机构复杂，驱动电路设计困难，制作、安装工艺流程复杂，成本相对较高。但该类型的振型控制效果比较理想，振型控制理论相对简单，制作、安装工艺要求也相对较低，对切削效果的控制比较容易[3-4]。目前，关于谐振型椭圆超声切削技术的研究较多，本文针对功率型的椭圆振型驱动电路的关键点之一——BUCK变换器开展研究。

根据文献[1-2,5]，椭圆超声波振型对切削质量和切削效果有非常大的影响。按照文献[3]的机械结构设计，只需控制好两个驱动臂的振动幅值即可控制刀具输出任意椭圆振型。这为椭圆超声振动改善切削效果和提高切削质量的研究奠定了良好的基础。根据文献[6-7]，压电堆在最佳激励振动频率附近时，振幅与激励交流信号的幅值正相关。而高频交流激励信号是由直流电压信号逆变产生的，所以如何实现精密调节直流供电电压成为了问题的关键。

本文的重点就是研究适合椭圆超声功率驱动的优化BUCK变换器模型，以便通过模型更好地指导BUCK变换器电路的设计和控制。为保证输出电压精密，可控性能好，本文仅研究电感中电流连续导电模式(continuous conduction mode，CCM)下的控制模型。

1　最优BUCK变换器模型的理论研究

为了提高BUCK变换器的模型与实际电路的吻合程度，建模时应尽可能考虑变换器电路中各电子元器件的寄生参数、纹波、扰动等因素对电路的影响，建立一个最优的BUCK变换器数学模型，使其能更好地指导应用电路的设计和分析。

建模思路如下：①将非理想器件视为理想器件与其寄生参数的串联，得到包含寄生参数的BUCK变换器等效电路；②计算开关器件的寄生参数在单周期内的平均值，计入电感支路；③用受控电流源代替有源功率开关IGBT、受控电压源代替续流二极管，计算一个周期内非理想脉冲宽度调制(PWM)开关器件的等效平均电路模型，得到开关变换器的大信号平均模型；④根据能量守恒，将寄生参数折算计入电感支路，得到简化的开关变换器大信号平均模型；⑤用占空比D控制的思想，推导出直流等效大信号电路模型，在此基础上分析包含扰动的交流小信号模型，导出小信号模型的相应传递函数，并进行稳态、动态小信号分析。

1.1变换器的大信号平均模型

基于大信号动态电路模型的假设[8-9]，图1a所示为BUCK变换器的标准电路模型，要使该模型更有实际指导意义，需计入各元器件的寄生参数，从而建立图1b所示的最优模型。其中，有源功率开关IGBT可看作理想开关S和导通电阻RS的串联；续流二极管D可视为理想开关D、导通压降VD和导通电阻RD的串联；RL、RC分别是滤波电感L和电容C的等效串联电阻[10-12]，R为负载电阻。假设功率开关S的开关周期为T，导通时间为Ton，则占空比D=Ton/T。

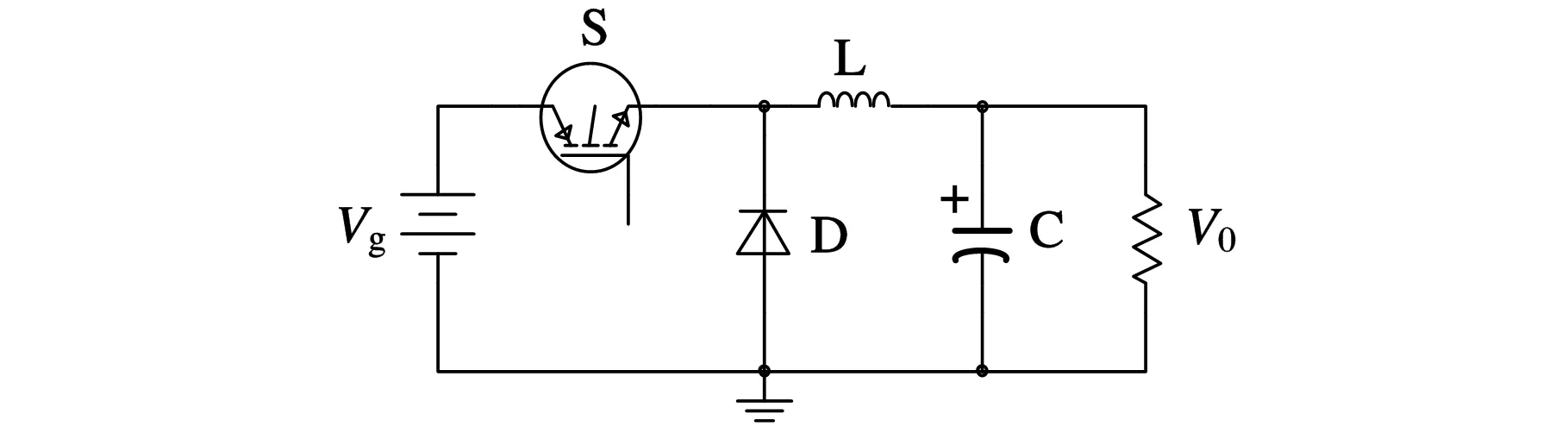
(a)标准BUCK变换器模型

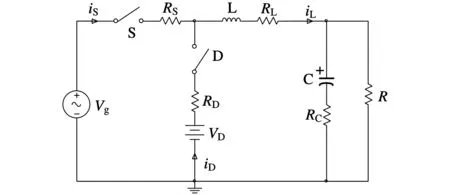
(b)包含寄生参数的最优BUCK模型图1　BUCK变换器的电路模型

在CCM模式下，考虑电感L中电流纹波的影响，变换器中流过电感、开关管以及二极管的电流波形如图2所示。

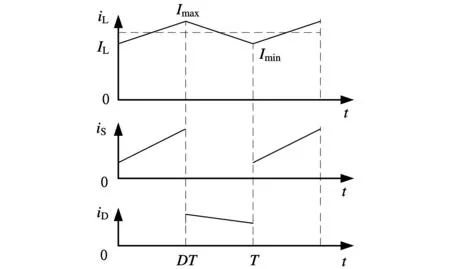
图2　CCM模式下各开关器件中的电流波形

假设实时电感电流iL(t)的单开关周期内最大电流为Imax，最小电流为Imin，则iL(t)为

(1)

式中，t为时间。

单开关周期平均电感电流IL为

(2)

电感电流纹波ΔiL为

ΔiL=(Imax-Imin)/2

(3)

则单开关周期的电感电流有效值ILrms为

(4)

通过计算电阻RL的功率损耗，根据能量守恒，可得其单周期等效平均电阻RLE:

(5)

对于功率开关S：当S导通时，开关S的瞬时电流iS(t)=iL(t)；当S关断时，iS(t)=0。则单开关周期内流过S的电流平均值IS为

(6)

因此，单周期内流过开关S的电流有效值为

(7)

同理，通过计算电阻RS的功率损耗，根据能量守恒，可得其单周期等效平均电阻RSE:

(8)

对于续流二极管D：当S导通，D截止时，D的瞬时电流iD(t)=0；当S关断，D导通时，iD(t)=iL(t)。同功率开关管S类似，可得其平均值电流ID、电流有效值IDrms、等效电阻RDE分别为

(9)

(10)

(11)

同理，考虑导通寄生电压VD，可计算续流二极管D的等效平均电压VE为

VE=(1-D)VD

(12)

将3个串联等效平均电阻合并，得到电感支路总的等效平均电阻RE:

RE=RLE+RSE+RDE=

(13)

最后，得到等效替换后CCM模式下的BUCK变换器简化电路模型，如图3所示。

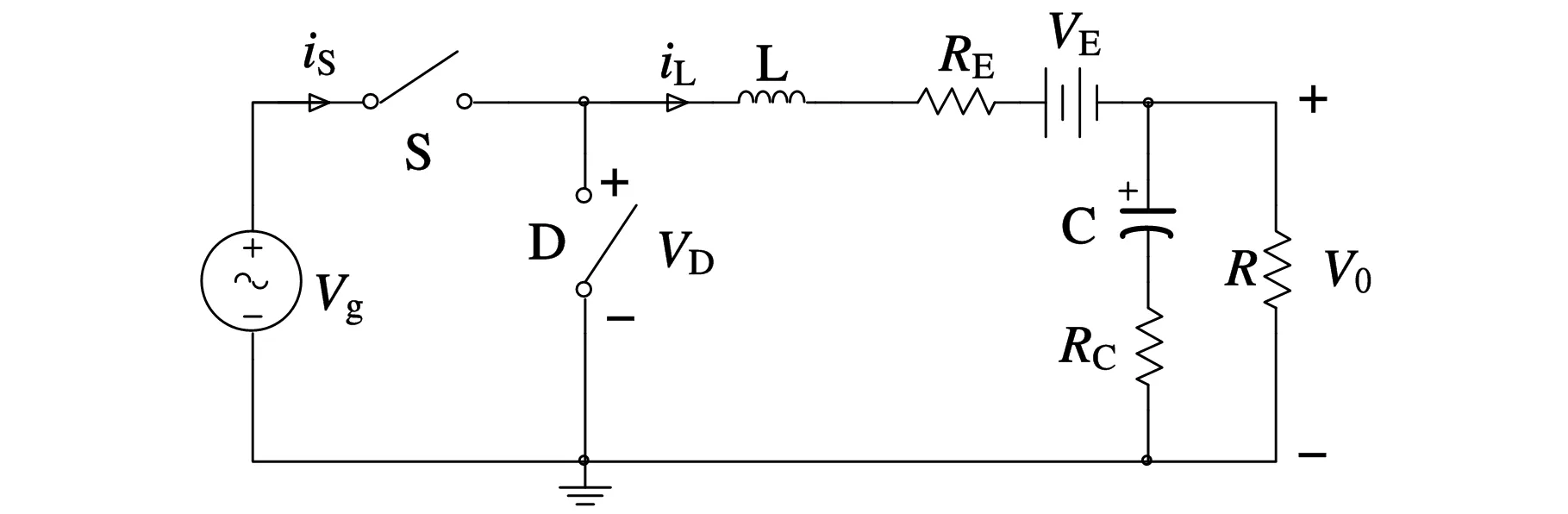
图3　CCM模式下的简化模型

(14)

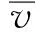
(15)

用受控电流源diL代替有源开关S，受控电压源dvg代替无源开关D，可得到BUCK变换器在CCM模式下的最优大信号平均等效电路模型，如图4所示。

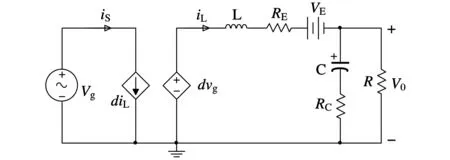
图4　CCM模式下的最优大信号平均等效模型

1.2直流等效电路模型

忽略小信号扰动，图4中假设各电压、电流信号以及占空比、受控电压源、电流源的平均分量等于它们对应的直流分量，即

vg=Vgv0=V0d=D

diL=dILdvg=DVg

假设电感L短路，电容C开路，并认为理想变压器能够变换直流，则受控电压源和电流源可以看作一个理想变压器[13]，如图5所示。

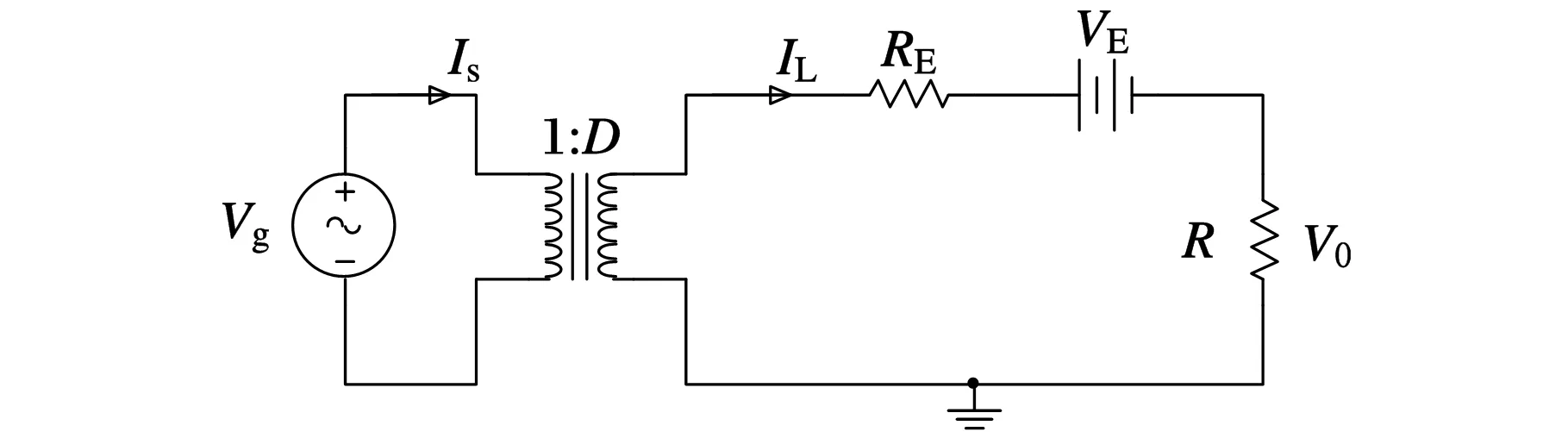
图5　BUCK变换器的直流等效模型

根据图5，结合式(12)、式(13)可得占空比为

(16)

1.3交流小信号等效电路模型

图4中，分离各信号及控制量的扰动，使其等于对应直流分量与交流小信号之和，即

则受控源diL、dvg分离扰动为

(17)

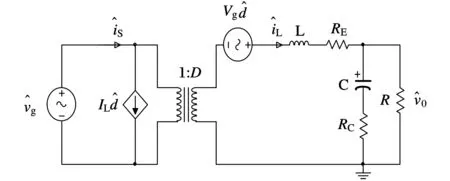
图6　CCM模式下交流小信号等效模型

对图6所示的交流小信号模型各参数进行s域变换，推导出其中两个重要的传递函数：

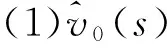
(18)

式中，ω0为自由谐振频率；Q为品质因数；ωz1为零点角频率。

(19)

Gvg(0)=DR/(R+RE)

Gvd(0)=VgR/(R+RE)

由此可知，其低频渐近线与变换器的等效寄生参数RE有关。

同理，令s→∞，可得小信号特性的高频渐近线：Gvg(∞)=0，Gvd=0。由此可知，高频渐近线与电容寄生参数RC无关。

2　CCM模式下BUCK变换器LC的优化分析

2.1临界电感分析[10-11]

图7所示的BUCK变换器，当IGBT功率开关S导通，输入电压Vg给电感充电，电感中的电流IL线性增大，直至超过负载电流I0时电容才开始充电；当功率开关S断开时，电感经续流二极管D继续给负载供电，IL逐渐减小，直至IL小于I0，此时电感、电容同时给负载供电。当IL降至0时，变换器工作在不连续导电模式(DCM)。

在功率开关S导通的时间Ton内，电感中的电流呈线性增大，峰值电感电流记为

ILmax=(Vg-V0)Ton/L+ILmin

(20)

式中，V0为负载输出电压，ILmin为电感电流最小值。

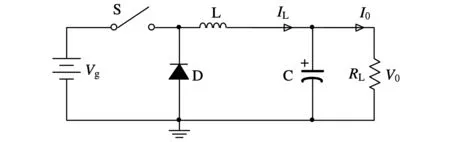
图7　BUCK DC-DC变换器

在开关S的周期T内，电容中电流iC(t)可表示为

(21)

将式(20)代入式(21)，在CCM模式下Ton=DT、V0=DVg，有

虽然中职学校开设了语文拓展教学这门课程，但是在实际教学中我们不得不面临的一个问题就是中职生的语文学习基础十分薄弱，对于拓展教学他们需要有太多的功课去做。这些问题主要体现在他们的口语交际能力比较差，主要表现为在一些人比较多的并且比较陌生的场合，他们与别人交流时就会出现一些结结巴巴、语无伦次、说话无中心、语言不连贯等不良现象。这些不足对于他们以后的工作面试来说，是非常不利的。这种不良现象并不是完全不能改正的，只要在平时的学习生活中有针对性地多加练习，就可以很好地克服。

(22)

因单周期中电容充放电守恒，即

(23)

将式(22)代入式(23)，得到电感中电流最大、最小值分别为

(24)

若ILmin=0，变换器工作在DCM模式；若ILmin>0，则变换器工作在CCM模式。此时，电感电流纹波可表示为

Δi=ILmax-ILmin=V0T(1-d)/L

(25)

因此，临界电感可通过ILmin= 0计算得出。通过式(24)及V0=RLI0(RL为负载)，可得临界电感LC：

LC=RL(1-d)T/2=RL(Vg-V0)/(2fSVg)

(26)

式中，fS为开关频率。

2.2理想电压波纹分析[12]

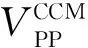
(t2-t1)(ILmax-I0)/(2C)

(27)

式中，ΔQ为单周期内电容充电电荷，t1、t2为电容中电流为0的时刻。

由式(22)有

(28)

将式(28)代入式(27)，可得CCM模式下的波纹电压：

(29)

由式(29)可知，输出电压波纹与开关频率fS的平方、滤波电感与电容的乘积LC成反比，与负载无关，随V0(1-d)增大而增大。因此，改善BUCK输出电压波纹的最有效途径是提高开关频率，但实际设计中因硬件条件限制，开关频率的提高往往受限。

3　最优BUCK变换器模型的仿真分析

文献[3]设计的二维椭圆超声功率切削驱动装置中，两个驱动臂的输出最大功率均为700W，超声波压电堆换能器的最佳谐振点为30kHz，对应BUCK变换器初始技术参数见表1。

表1　变换器模型设计初始参数

3.1模型电容与电感的优化设计

根据CCM模式下临界电感、电容的结论，可计算出临界电感LC≈197.7μH，其中，V0取调节范围最小值。

由式(25)可知，电感电流纹波与V0(1-d)成正比，则最大纹波为

Δi=110×2×10-5×(1-0.5)/L≤1(A)

得L≥1.1mH。该值大于LC，满足CCM模式工作的要求。选用高磁导率的铁氧体磁芯，选直径为0.8mm的电磁线，订制电感串联内阻RL=0.2Ω。

根据滤波器电容选择原则：在220V交流输入条件下，按照1μF/W的容量选取[14]，则滤波电容C=700μF，根据电容标称值序列，取C=680μF。记等效串联电阻(ESR)为RC，则

考虑电流纹波及RESR的影响，实际输出最大电压波纹ΔV为

则总体电压波纹满足设计要求。

3.2模型关键元器件确定及相关参数设计

根据初始参数要求以及电流、电压波纹要求，BUCK变换器中关键器件选择见表2。

表2　变换器关键元件选择

按照输出最大电压计算最优模型的占空比：

D=

(30)

电感支路总的等效平均电阻RE为

RE=[0.2+0.69×0.078+(1-0.69)×0.05]×1.0133=0.2729(Ω)

(31)

根据上述参数，可计算出模型相关参数如下：

ω0=

(32)

{[30×(0.2729+0.229)+0.2729×0.229]×680×10-6+

1.1×10-3}=2.3

(33)

(34)

3.3系统模型分析

3.3.1系统模型的仿真分析

将式(32)～式(34)代入式(18)、式(19)可得优化后的BUCK变换器相关传递函数：

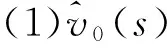
(35)

(36)

根据式(35)、式(36)对应的Gvg(s)、Gvd(s)传递函数表达式，在MATLAB中分别生成如图8a、图8b所示的Bode图。

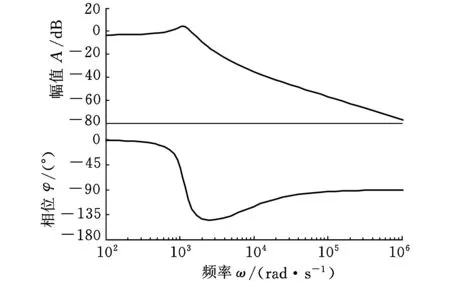
(a)Gvg(s)Bode图

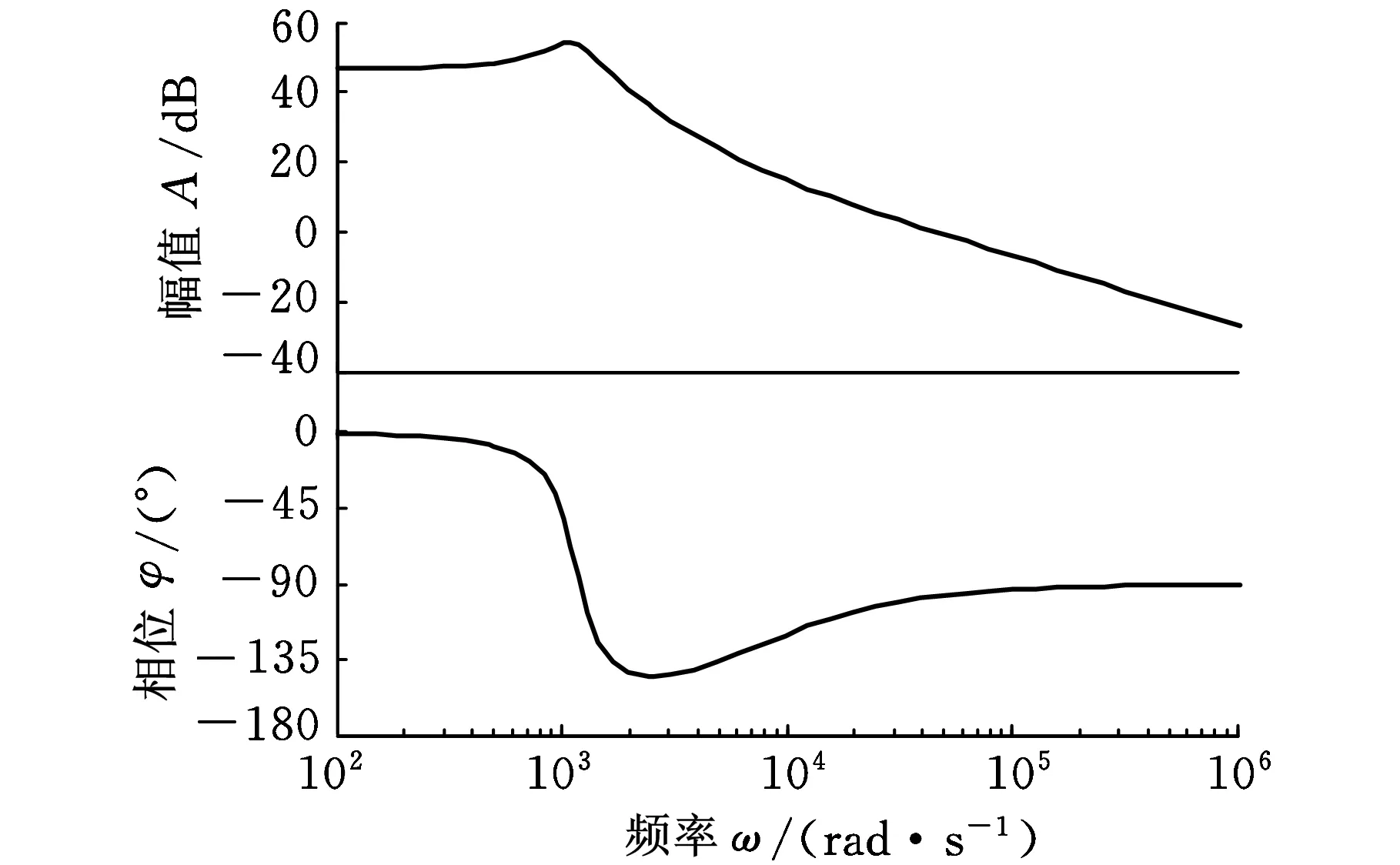
(b)Gvd(s)Bode图图8　MATLAB绘制的Bode图

3.3.2系统模型的实验分析

根据模型的相关参数，设计图9所示的模型验证电路，由于电路中开关管S和续流二极管D均需散热，故电路设计时安装在PCB板的反面，散热片直接与金属机柜接触，以改善散热效果。

图9　BUCK模型验证电路

将验证电路接入Agilent 35670A动态信号分析仪，通过逐次调整输入信号的频率、幅值、占空比，分别观测输出信号的增益、相位，整理记录数据后生成图10所对应的验证轨迹。

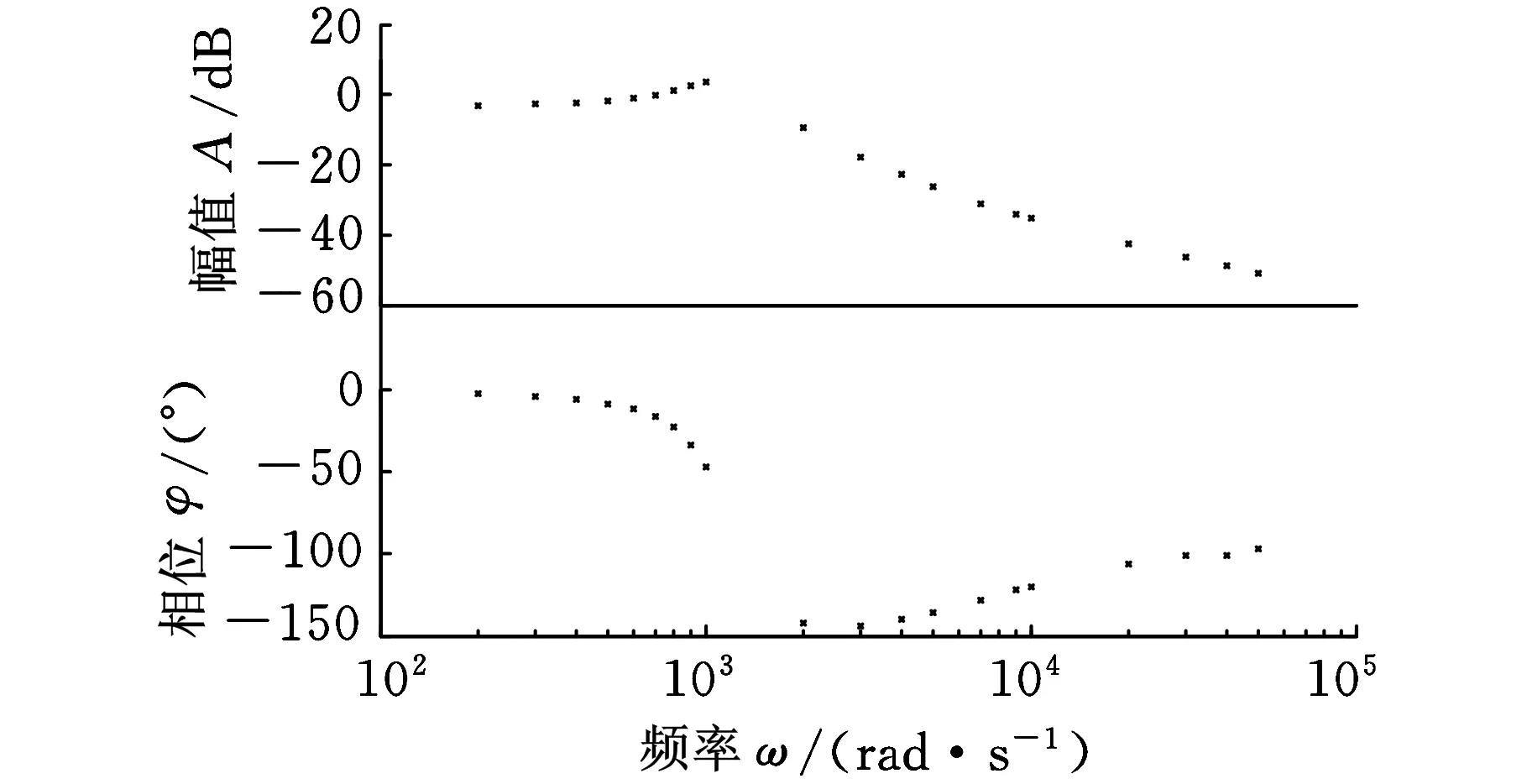
(a)Gvg(s)的实测幅相轨迹图

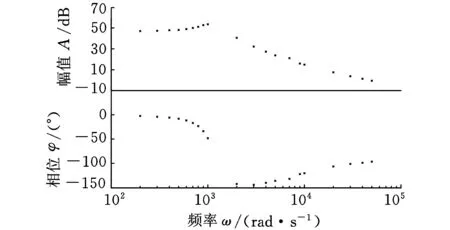
(b)Gvd(s)的实测幅相轨迹图图10　Gvg(s)、Gvd(s)的验证轨迹图

在输入电压均为DC220V的前提下，调节占空比D，分别测试其对应的实际输出电压V0，并与理论输出电压对照，可得表3所示的数据结果。

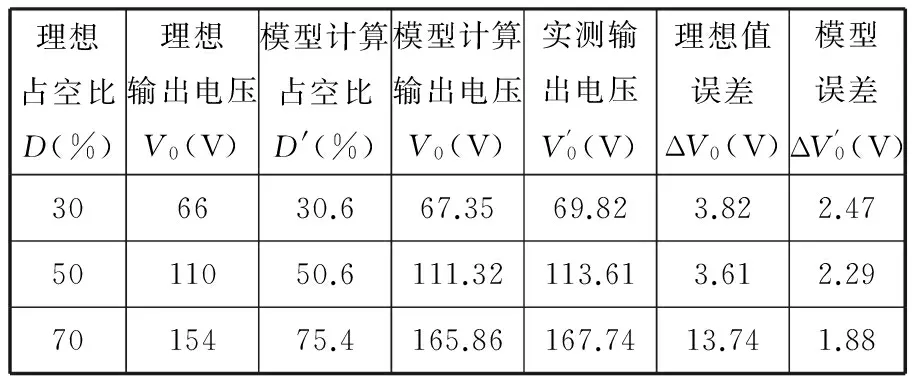
表3　占空比调节对比数据

4　结语

对照图8、图10可以看出，对于较高电压、以IGBT为开关的、功率接近千瓦的适用于超声波驱动的最优BUCK模型与验证电路能较好地吻合，为进一步分析其控制模式、电路稳定性打下了良好的基础。

由表3可以看出：当占空比D较小时，实际输出电压与理论值误差较小；当占空比D逐渐增大时，输出电压较之理论值越来越大，本文BUCK模型计算明显体现出优势，其误差逐步减小。

[1]季远,李勋,张德远.超声椭圆振动精密切削[J].航空制造技术,2005(4):92-95.

Ji Yuan, Li Xun, Zhang Deyuan.Ultrasonic Elliptical Vibration Cutting Precision[J].Aviation Manufacturing Technology , 2005(4)：92-95.

[2]马春翔,胡德金.超声波椭圆振动切削技术[J].机械工程学报,2003,39(12):67-70.

Ma Chunxiang, Hu Dejin.Ultrasonic Elliptical Vibration Cutting[J].Chinese Journal of Mechanical Engineering, 2003,39(12):67-70.

[3]陈明方,邹平，于泽旭，等.功率型椭圆超声振动切削机构的研究[J].机械设计与制造,2014(3)：8-11.

Chen Mingfang, Zou Ping,Yu Zexu,et al.Study on the Cutting Mechanism of Power Type Elliptic Ultrasonic Vibration[J].Machinery Design & Manufacture, 2014(3):8-11.

[4]赵亮,祝锡晶,陆志猛.功率超声车削加工装置的设计与仿真分析[J].机械设计与制造,2010(12)：20-22.

Zhao Liang, Zhu Xijing, Lu Zhimeng.The Design of Power Ultrasonic Vibration Device for Turning and Simulation Analysis[J]. Machinery Design & Manufacture, 2010(12)：20-22.

[5]马春翔,社本英二.超声波椭圆振动切削提高加工系统稳定性的研究[J].兵工学报,2004,25(6):752-756.

Ma Chunxiang,Shamoto E. Ultrasonic Elliptical Vibration Cutting to Improve the Study of Stability of the Maching System[J].Journal of Armaments Factories, 2004, 25(6)：752-756.

[6]陈明方,邹平,韩钢,等. 数控辅助超精密定位工作平台的研究[J].东北大学学报(自然科学版),2013, 34 (6): 875-879.

Chen Mingfang, Zou Ping, Hang Gang,et al.Study on Ultra Precision CNC Auxiliary Working Platform[J]. Journal of Northeastern University (Natural Science),2013, 34(6): 875-879.

[7]陶继增,王中宇,李程.压电叠堆在正弦电压激励下振动位移特性的研究[J].计测技术，2006(6)：20-23.

Tao Jizeng, Wang Zhongyu, Li Cheng.Research on Vibration Displacement Characteristic of Piezoelectric Ceramics under Sine Voltage Excitation[J].Metrology & Measurement Technology, 2006(6):20-23.

[8]Zhao Yibo， Luo Xiaoshu， Fang Jinqing.Study on Stability of the Voltage-mode DC-DC Converters[J].Annual Report of China Institute of Atomic Energy, 2004(1)：84-87.

[9]欧阳长莲,严仰光,章国宝.同步整流BUCK变换器断续工作模式建模分析[J].电工技术学报,2002,17(6):53-58.

Ouyang Changlian,Yan Yangguang, Zhang Guobao. Modeling Analysis of Synchronous Rectifier BUCK Converter in DCM[J].Journal of Electrotechnics, 2002,17(6):53-58.

[10]刘树林,钟久明,刘健.BUCK-Boost变换器的最小电感和电容设计考虑[C]//2011中国电工技术学会学术年会论文集. 北京,2011:716-721.

[11]付园园,姚素英,徐江涛,等.BUCK DC-DC变换器电感的优化设计[J].南开大学学报(自然科学版),2012,45(6):33-40.

Fu Yuanyuan, Yao Suying,Xu Jiangtao,et al.Optimization of Inductance for BUCK DC-DC Converter[J].Acta Scientiarum Naturalium Universitatis Nankaiensis, 2012,45(6):33-40.

[12]刘树林,刘健,寇蕾,等.BUCK DC/DC变换器的输出纹波电压分析及其应用[J].电工技术学报,2007,22(2):91-97.

Liu Shulin, Liu Jian,Kou Lei,et al.Analysis of Output Ripple Voltage of BUCK DC/DC Converter and Application[J]. Journal of Electrotechnics, 2007,22(2):91-97.

[13]解光军,徐慧芳.峰值电流模式控制非理想BUCK变换器系统建模[J].中国电机工程学报,2012,32(24):52-58.

Xie Guangjun,Xu Huifang. Modeling of Current Programmed Mode Non-ideal BUCK Converter Systems[J]. Proceedings of the CSEE, 2012,32(24):52-58.

[14]蔡宣三,龚绍文.高频功率电子学[M].北京：中国水利水电出版社,2009.

(编辑陈勇)

Optimization BUCK Model Used in Elliptic Ultrasonic Power Cutting Driving Device

Chen Mingfang1,2Zou Ping1He Yu1Wu Hao1Zhang Yongxia3

1.Northeastern University，Shenyang，110089 2.Shenyang Polytechnic College，Shenyang，110045 3.LiaoShen Industrial Group Co.,Ltd.，Shenyang，110045

Based on elliptic ultrasonic power cutting driving device of the BUCK converter model optimization research, fully considering the influence of each component parasitic parameters on the model, at the same time the LC optimization design was carried on the thorough analysis, an optimized converter model was designed and the appropriate verification circuit was made. Through analyses of two important BODE diagrams of transfer function model test of the model and simulation analysis, the results prove that the model better reflects the dynamic performance of the real circuit, better guides the design of the converter.

ultrasonic power cutting drive；elliptical vibration mode；BUCK converter；model

2014-09-01

辽宁省教育厅科学研究一般项目(L2014556)；辽宁省科技厅博士启动基金资助项目(20141096)；沈阳市科技局科技攻关专项(F14-124-9-00)

TG663< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.01.004

陈明方，男，1975年生。东北大学机械工程与自动化学院博士研究生，沈阳职业技术学院电气工程学院副教授。主要研究方向为超声切削技术、特种数控机床、测控系统。邹平，男，1963年生。东北大学机械工程与自动化学院教授、博士研究生导师。何宇，男，1989年生。东北大学机械工程与自动化学院博士研究生。吴昊，男，1990年生。东北大学机械工程与自动化学院博士研究生。张永霞，女，1978年生。辽沈工业集团有限公司108分公司高级工程师。