面向再制造复杂机械产品装配过程的质量控制点公差带在线优化方法

刘明周　邢玲玲　刘从虎　张　淼

合肥工业大学，合肥，230009

面向再制造复杂机械产品装配过程的质量控制点公差带在线优化方法

刘明周邢玲玲刘从虎张淼

合肥工业大学，合肥，230009

为提高再制造零部件利用率并提升再制造复杂机械产品的装配精度，提出了一种面向再制造复杂机械产品装配过程的质量控制点公差带在线优化方法。在分析再制造复杂机械产品装配特点的基础上，对关键工序的质量控制点公差带进行细粒度划分；从装配精度角度出发，综合考虑装配过程中的质量损失和成本差异，以尺寸链为约束，构建了公差带优化模型，并研究了基于遗传算法的模型求解过程；在此基础上，提出了基于历史数据的正向推理模式，以及基于装配实时信息的逆向推理模式，推导出装配优化方案集并对车间异常情况作出及时响应；最后，开发出再制造发动机装配过程在线质量控制系统原型，验证了该方法的可行性和有效性。

再制造； 装配过程；质量；公差带在线优化

0　引言

再制造是废旧产品高科技修复和升级的产业化，其产品质量问题一直备受关注。近年来，国内外学者从不同角度对再制造产品质量控制机制问题进行了研究：在生产计划调度方面，Jin等[1]对回收产品质量不确定性条件下的再制造系统最优控制策略进行了研究；Tang等[2]在回收产品质量不确定情况下，运用开放排队网络构建了再加工系统模型；苏春等[3]研究了质量成本和需求替代的再制造生产计划；文献[4-5]对再制造多产品经济批量排产问题进行了研究。在再制造设计方面，牛同训[6]提出了一种再制造公差设计优化数学模型，该模型能够有效保证和提高再制造产品质量。在废旧零部件回收方面，Ferguson等[7]考虑到回收废旧毛坯质量的不同，研究了再制造过程中质量分级的价值。在再制造零部件质量评价方面，Zhou等[8]基于模糊层次分析法提出了量化废旧轮式装载机零部件可重用度的质量评价模型。

上述研究为再制造产品质量控制作出了极大贡献。但是，由于诞生时间较短，多学科交叉的再制造工程仍然存在一些基础技术问题没有解决[6]。再制造装配不仅是决定再制造产品质量和性能的重要环节，而且对再制造工期和再制造成本等具有重要的影响。再制造装配过程具有高度复杂性和动态不确定性[9]，在环保节约的大前提下，如何在动态不确定环境中实现批量化、规模化的再制造装配过程准确、实时的在线质量控制，在可控成本范围内提高再制造产品质量，成为再制造企业面临的主要问题之一。

本文结合笔者所在项目组在再制造质量管理[9]、公差带在线优化[10]和质量控制模型[11]方面前期研究的基础上，以再制造发动机为背景，针对再制造复杂机械产品装配的特点，对装配过程的质量控制点公差带在线优化方法进行了研究，为提升再制造产品装配质量提供理论和技术支持。

1　方法概述

1.1再制造复杂机械产品装配的特点

再制造复杂机械产品装配具有以下几个特点。

(1)再制造复杂机械产品装配零部件主要由三种零部件组成：再利用件、再修复件和新件。其中，再利用件和再修复件的质量控制点的公差带离散程度大、中心偏移，导致再制造装配质量不稳定程度较传统制造大。

(2)使用新件和再利用件或将零部件修复到不同等级的成本和质量损失不同，并且使用不同公差带等级零部件的质量损失和装配成本不同。

(3)为了有效利用再制造资源，减少生产成本，再制造装配总是尽可能使用再利用件和再修复件，导致再制造装配过程质量控制不确定因素增加，装配精度难以保障，进而导致产品返修率和售后服务成本增大。

(4)不同公差带等级零部件装配在一起导致装配方案呈现多样化、质量控制点属性不确定等特点，影响装配质量。

同时，再制造复杂机械产品装配过程实际情况复杂，订单需求变化、零部件短缺、质量事故等异常状况时有发生。这种高不确定性的再制造装配过程，迫切需要一种再制造装配在线质量策略，来综合考虑再制造零部件的利用率和再制造装配精度。

1.2在线优化方法

在对上述再制造复杂机械产品装配特点进行研究的基础上，本文提出了面向再制造复杂机械产品装配过程的质量控制点公差带在线优化方法，其基本流程如图1所示。该方法以再制造装配精度、装配成本、质量损失、装配尺寸链和质量控制点公差带为约束条件，建立公差带优化模型，在智能优化算法的支持下，综合考虑历史数据和车间实时信息，推导出再制造装配优化方案集，目的是提高再制造复杂机械产品的装配精度和再制造零部件利用率。

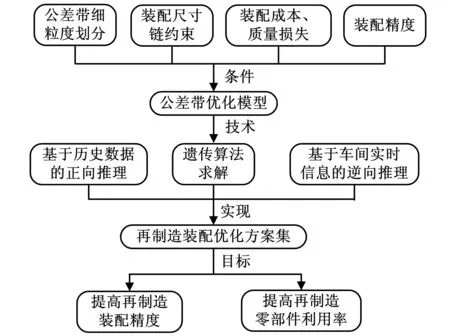
图1　在线优化方法流程

2　面向再制造复杂机械产品装配过程的质量控制点公差带优化模型

面向再制造复杂机械产品装配过程的质量控制点公差带优化模型是在尺寸链约束条件下，以质量损失和装配成本最小化为目标，通过公差带分级选配减少再制造装配质量的不稳定性，运用遗传算法动态配置方案，优化装配过程，确保产品装配精度。

2.1基于质量控制点公差带细粒度划分的分级选配

假设某再制造复杂机械产品装配过程共有n道关键工序，即S1,S2,…,Si,…,Sn，工序Si上对应m个质量控制点，对第i道工序中的第j个质量控制点公差带进行细粒度划分，将原始公差带分为γ个公差等级，即

Tij={Tij[1],Tij[2],…,Tij[γ]}

i=1,2,…,nj=1,2,…,mγ=1,2,…

Tij将原始公差带划分成γ段连续区域。公差带等级γ主要由长期从事再制造复杂机械装配工作的专家的知识和经验，以及国内外有关再制造机械产品质量控制和优化的专著和文献决定。

2.2优化模型

模型中的约束函数和目标函数如下。

(1)尺寸链约束函数。用户输入系统的尺寸数据xij主要满足尺寸链约束：假设复杂机械产品装配过程中第i道关键工序的第j个质量控制点处尺寸链共有p+q+1个环，其中增环的数量为p，减环的数量为q，封闭环基本尺寸为Aij。为确保装配质量，采用极值法，即封闭环的基本尺寸必须大于或等于增环的基本尺寸之和减去减环的基本尺寸之和，即

(1)

(2)目标函数。各个不同等级的零部件由于公差带的不同，偏离目标值的程度不同，造成的质量损失不同。不同等级零部件的装配成本(包括设备、人力、能源、管理等成本)不同，因此,不同等级的零部件装配成组件的成本也不同。为保证再制造产品装配精度，同时降低装配成本，本文以质量损失和装配成本最小化为目标建立目标函数。

①第i道工序的第j个质量控制点公差带等级为φ的质量损失函数为

Lij=k(dij[φ]-Dij[φ])2/Cpmi

(2)

k=Aij/(Δij[φ])2φ=1,2,…,γ

式中，φ为公差带等级；k为质量损失常数；Δij[φ]为公差带等级φ对应的公差带范围；dij[φ]、Dij[φ]分别为第i道工序的第j个质量控制点的测量值、公差带等级φ的目标值；Cpmi为第i道工序基于田口质量损失的工序能力指数[10]。

②第i道工序的第j个质量控制点公差带等级为φ的装配成本函数为

Gij=Gij[φ]

(3)

式中，Gij[φ]为第i道工序的第j个质量控制点公差带等级为φ零部件的装配成本。

③目标函数为

(4)

ωl+ωg=10≤ωl≤10≤ωg≤1

式中，ωl、ωg分别为质量损失、装配成本对总损失的影响系数；xij φ为第i道工序的第j个质量控制点选用公差带等级为φ的零部件。

2.3基于遗传算法的模型求解

鉴于遗传算法[12]在寻求全局最优解方面具有高效率参数优化的特点，本文采用遗传算法求解面向再制造复杂机械产品装配过程的质量控制点公差带优化模型，求解过程如下。

(1)编码。本文采用浮点数进行编码，根据模型的假设条件，其编码规则如下：①按再制造复杂机械产品关键装配工序排列顺序，并进行编码，依次为1,2,…,n。②对装配工序中的质量控制点按一定的顺序排列，并进行编码，依次为1,2,…,m。③按照质量控制点公差带进行细粒度划分，并进行编码，依次为1,2,…,γ。④抗体的一个基因值对应一个装配工序质量控制点的公差等级的配置方案。⑤一个抗体对应再制造装配工序质量控制点的公差等级配置的一个方案。

(2)个体适应度函数。由于本文为最小值的优化问题，且应用均匀排序选择，故能保证适应度函数在选择中概率非负，又能保证种群中个体适应度在数值上相差不是太大进而影响计算性能，设适应度函数为

fit(F)=1/(F+c)

由于目标函数始终为正值，故c=0。由适应度函数可以看出，目标值越小，适应度值就越大，在选择遗传算法操作中被选中的相对概率就会越大。

(3)编码与种群初始化。为了保证在遗传算子操作过程中不产生候选装配工序质量控制点的公差等级以外的个体，采用装配工序质量控制点的公差等级在其初始空间中的排列序号进行编码，并用二进制表示。为避免陷入局部最优而出现“早熟”现象，本文采用随机方式生成初始种群。

(4)遗传算子。①选择算子：为保护优秀个体，本文对群体中的所有个体按照其适应度从大到小进行排序，基于上述排序结果来分配各个体被选中的概率。②交叉算子：本文采用均匀交叉方式，交叉概率在[0,1]内选取。③变异算子：对应于均匀交叉算子，采用均匀变异进行变异操作，变异概率则选择一个较小的值。

(5)遗传优化步骤。根据以上设置，基于遗传算法求解面向再制造复杂机械产品装配过程的质量控制点公差带优化模型，其求解步骤如图2所示。

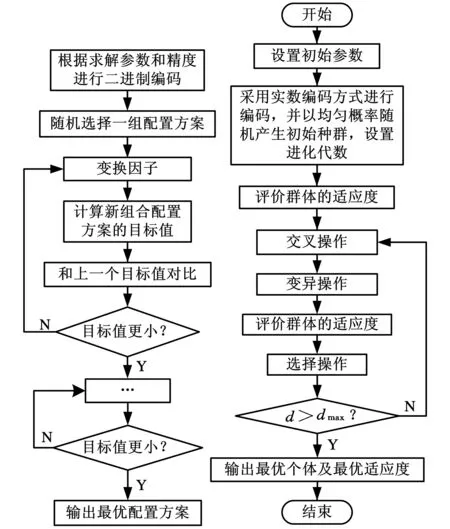
图2　遗传算法求解步骤

3　在线优化推理策略

3.1推理原理

推理过程是再制造复杂机械产品装配过程质量控制点公差带在线优化系统的核心。推理方法主要有正向推理、逆向推理或正逆向结合的双向推理，并包含精确推理和非精确推理[13]。由于再制造装配生产过程中零部件属性的差异及复杂、动态、非线性耦合的不确定因素对产品装配质量的影响，本文提出的再制造复杂机械产品装配过程质量控制点公差带在线优化系统推理策略采用正向和逆向相结合的混合推理模式，即基于历史数据的正向推理模式以及基于装配实时信息的逆向推理模式。3.2基于历史数据的正向推理

再制造装配方案具有多样化特点，如何在诸多装配方案中按照既定的目标选出最理想的方案用以指导修复作业和生产计划是正向推理策略需要解决的问题。基于历史数据的正向推理过程如图3所示。

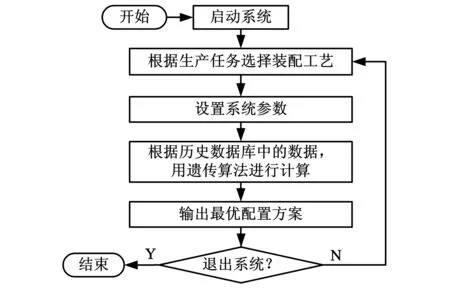
图3　正向推理过程

(1)启动在线优化系统，根据生产任务选择工艺，预先设置精度等级、成本及质量损失系数等参数。

(2)系统根据历史数据对零部件进行整合编码，按照第2节建立的模型和约束，运用遗传算法进行优化计算，推导出最优配置方案。

正向推理推导出的装配方案主要用以指导再制造零部件修复作业和装配车间生产计划的制定，为生产过程管理、车间各类资源优化配置以及物料实时供应等提供指导。

3.3基于装配实时信息的逆向推理

再制造装配过程复杂，订单需求变化、零部件短缺和质量事故等异常状况时有发生，如何在环保节约的前提下对其作出及时响应，在提高装配产品质量的同时降低成本，是逆向推理过程需要解决的主要问题。基于装配实时信息的逆向推理过程如图4所示。

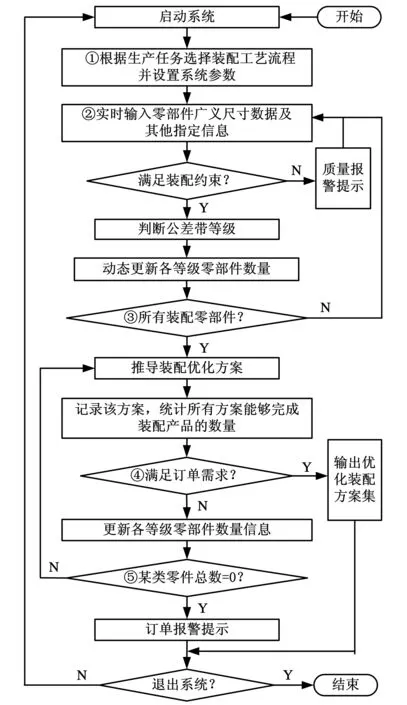
图4　逆向推理过程

(1)启动在线优化系统，根据生产任务选择工艺，预先设置精度等级、成本及质量损失系数等参数。(同3.2节中(1))

(2)利用在线实时信息采集技术获得再制造装配零部件广义尺寸数据及其他属性信息，并将其录入系统。系统根据约束条件判断该零部件是否满足装配要求。若不满足则系统给出质量报警，提示该零部件存在质量问题并将该零部件进行标记暂存处理，然后继续输入其他零部件信息；若满足装配约束条件，系统根据数据库中参数及规则判断零部件公差带级别，动态修改不同等级零部件的数量和其他信息。

(3)当所有再制造装配零部件指定信息录入系统后，系统根据实际生产需求，针对整个装配工艺流程或者某道工序按照模型中的目标和约束推导装配优化方案，标记该方案号为1，记录该方案并统计方案1装配产品的数量。

(4)判断方案1完成的装配产品数量是否满足订单需求。若满足则输出方案1；若不满足则将各等级零部件数量减去方案1使用各类零部件数量。

(5)系统对更新后的零部件数量进行判断，判断是否出现某类零部件件数量为零的情况，即该类零部件各等级数量均为零。若某类零部件数量为零，则系统给出报警提示零部部件短缺；若各类零部件均有剩余则进入下一步。

(6)系统对剩余零部件再次进行智能计算，推导出装配优化方案，标记该方案号为2，记录该方案并统计方案1和方案2完成装配产品的数量总和。

(7)判断方案1和方案2完成的装配产品数量总和是否满足订单需求。若满足则输出方案1和方案2；若不满足则动态更新零部件数量信息，然后判断是否出现零部件数量为零的情况，重复步骤(5)。

(8)若完成方案1和方案2后各类零部件均有剩余，则重复步骤(6)，推导出方案3。依次迭代，直到满足订单需求。

逆向推理过程能够对订单需求变化、零部件短缺和质量问题做出及时响应，动态输出装配优化方案集，实现对再制造复杂机械产品装配过程质量控制点公差带的在线优化，指导实际装配过程，并向车间生产管理人员提供科学决策支持。同时逆向推理推导出的装配优化方案集考虑到再制造资源利用的问题，提高了再制造件和再利用件的利用率。

4　系统实现

发动机具有较好的再制造性[14]，本文以某重载发动机再制造企业为依托，开发出面向再制造复杂机械产品装配过程的质量控制点公差带在线优化系统原型。该企业生产的再制造发动机种类很多，以斯太尔系列发动机为例，其装配零部件大部分是再利用件和再修复件，种类繁多，零件公差带离散程度大，导致装配质量不稳定程度增大，并且装配方案呈现多样化特点。为此，根据本文提出的再制造复杂机械产品装配过程质量控制点在线优化方法，设计开发了该企业再制造发动机装配过程在线质量控制系统原型，以活塞连杆组装配序列为例，介绍系统集成运行和应用情况。

(1)系统首先根据生产任务选择WD615再制造发动机装配工艺流程，活塞连杆组装配为第四个装配序列，工序号为20。编号为KMSX-002连杆的关键质量控制点是大头孔径，该质量控制点的标准公差带范围是[87.5,89]mm，设一级公差带范围是[87.5,88]mm，二级公差带范围是(88,88.5]mm，三级公差带范围是(88.5,89]mm。利用在线实时信息采集技术获得连杆基本信息，并按要求录入系统，如图5所示。

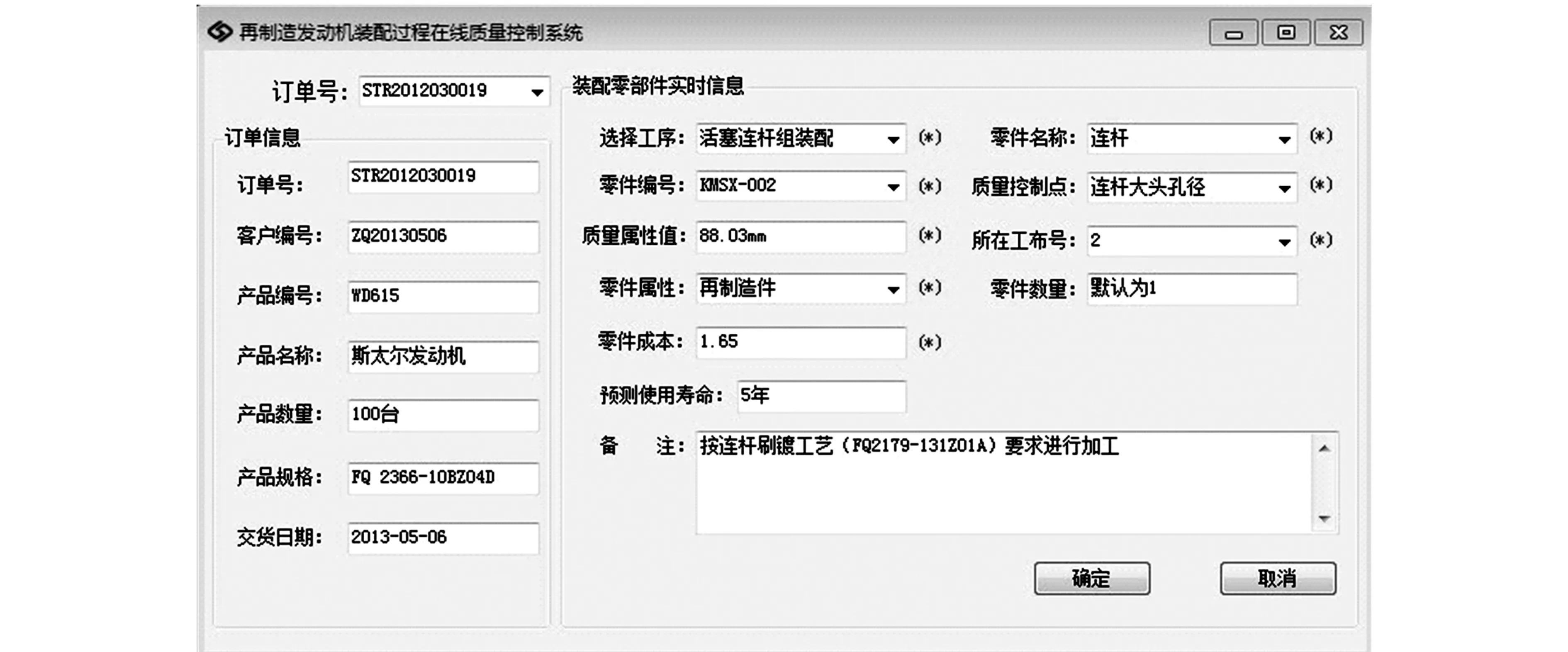
图5　再制造发动机连杆实时信息录入

(2)由图5可知，该连杆的大头孔径为88.03mm，该值满足装配要求，并根据事先划分的公差带等级判断该值属于二级，动态更新数据库中各等级零件数量。当活塞连杆组所有装配零件指定信息录入系统后，系统根据实际生产需求，针对工序20，根据在线质量控制策略推理模型中的目标和约束推导出最优装配方案，标记该方案号为1，记录该方案并统计方案1装配活塞连杆组的数量为9。如图6、图7所示。

(3)显然方案1完成的9件活塞连杆组不能满足订单需求，系统记录方案1详情并在原各等级零件数量的基础上减去方案1使用的零件数，动态更新各等级零件数量信息。完成方案1后各类零件均有剩余，系统再次推导剩余零件的最优装配方案，即方案2。统计方案1和方案2完成活塞连杆组的总数量，并判断是否满足订单需求，重复步骤(3)，直到满足订单100台的要求。最后输出WD615再制造发动机活塞连杆组装配优化方案集，如图8所示。

若在推理过程中出现零部件供应不足、质量属性值不满足装配条件等异常情况，则系统会及时给出报警提示，图9所示为报警信息设置情况。

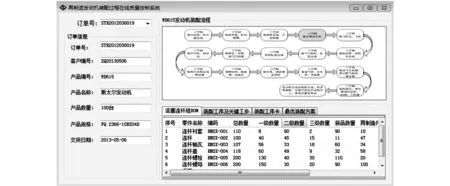
图6　WD615再制造发动机活塞连杆组BOM全信息详情

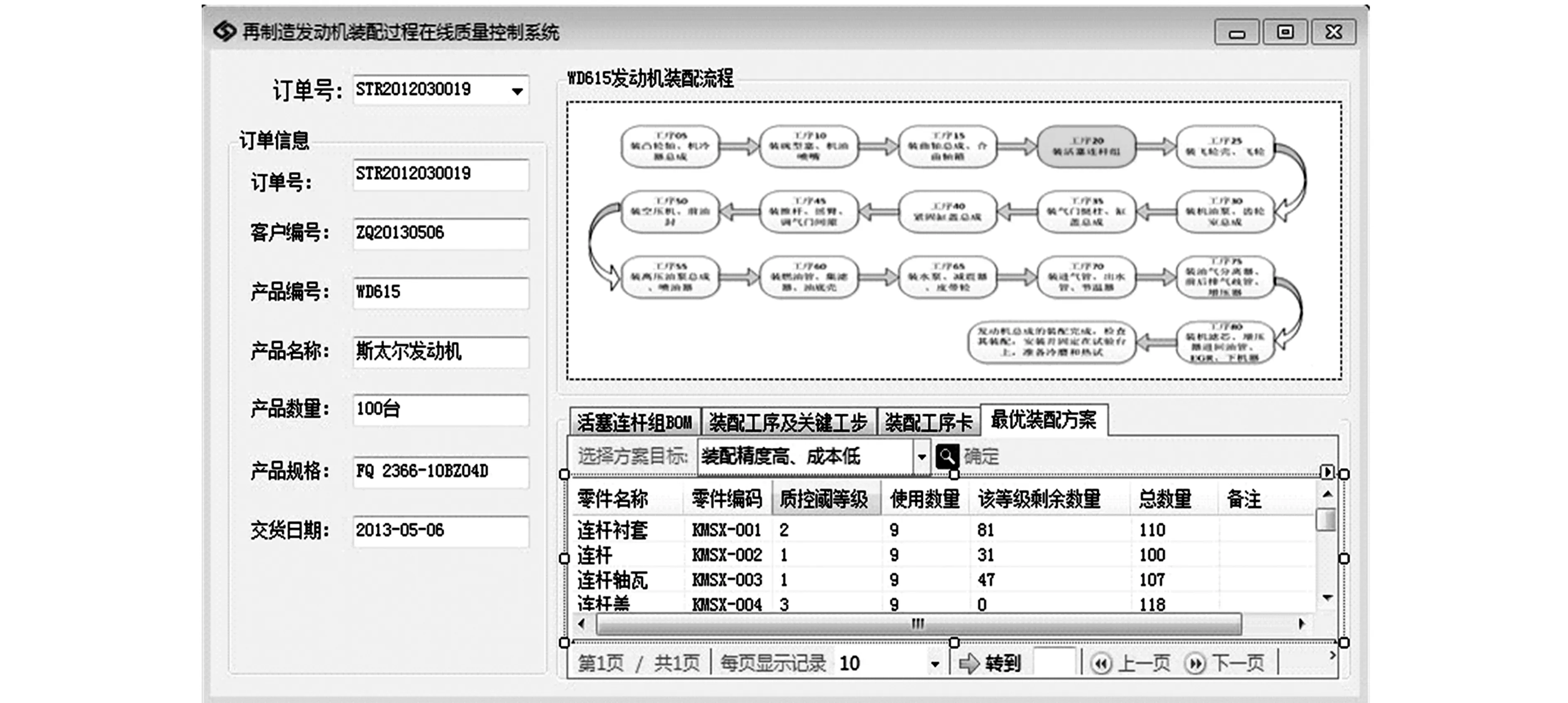
图7　WD615再制造发动机活塞连杆组最优装配方案

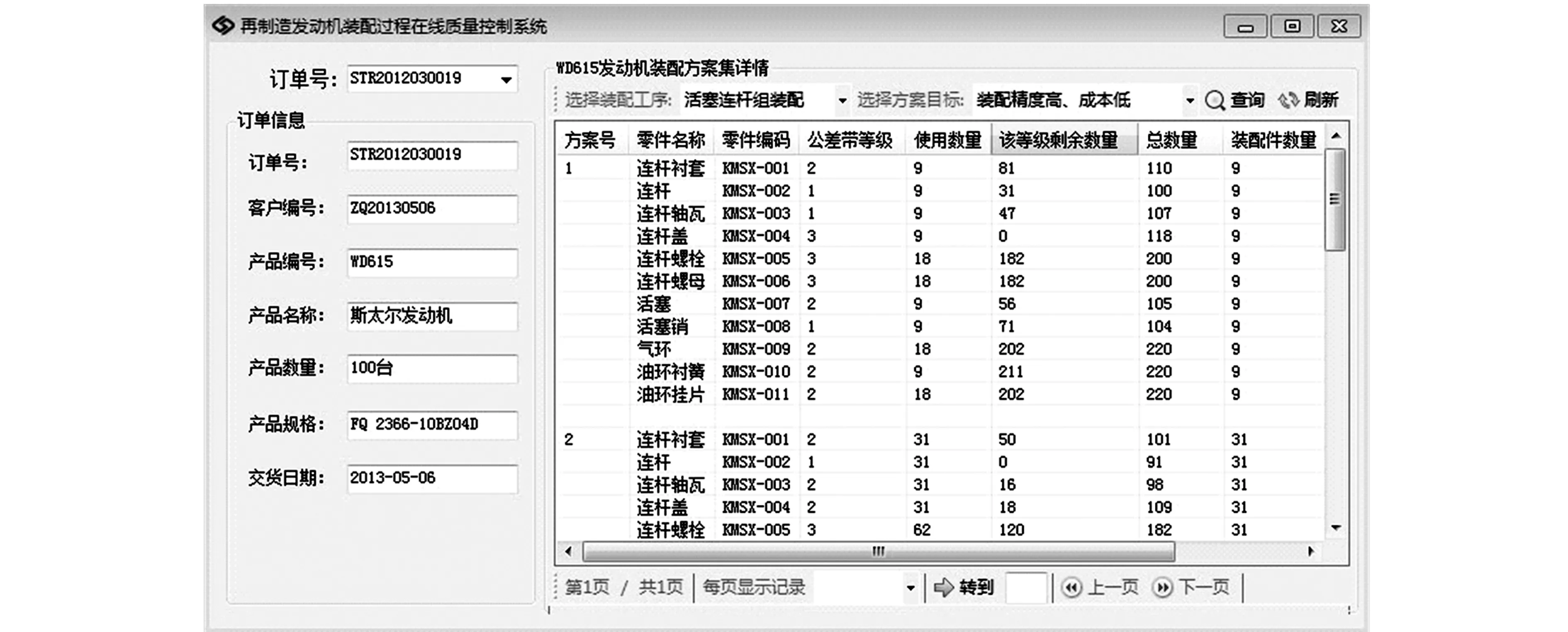
图8　WD615再制造发动机活塞连杆组装配优化方案集

图9　报警信息设置

装配车间机车试车后2011年传统选配和2012年实行在线优化方法后的装配不合格率、发动机返修率、售后赔偿金额对比见表1。2012年统计数据显示：与2011年相比，装配车间实施在线优化方法以来，装配车间再制造发动机合格率提高了0.87%；装配车间再制造发动机返修率平均下降5.22%；企业售后索赔成本降低280.5万元，同比下降29.7%。

表1　2011年和2012年装配不合格率、发动机返修率和售后赔偿金额对比

注：为保护企业权益，表中数据是经过处理后的数据。

5　结论

(1)本文在研究再制造复杂机械产品装配特点的基础上，从装配精度角度出发，对关键工序的质量控制点公差带进行细粒度划分，综合考虑装配过程中质量损失和成本差异，以尺寸链为约束，构建了公差带优化模型，并研究了基于遗传算法的模型求解过程。

(2)提出了基于历史数据的正向推理模式，以及基于装配实时信息的逆向推理模式，推导出再制造装配优化方案集，提高了资源利用率，并根据推理规则和约束条件对零部件质量问题、零部件短缺等异常情况做出及时响应，实现了对再制造复杂机械产品装配过程的在线质量控制，动态指导实际装配过程。

(3)以某重载发动机再制造企业为依托，开发出再制造发动机装配过程在线质量控制系统原型，验证了该方法的可行性和实用性，为提高再制造复杂机械产品的装配精度与再制造资源利用率提供了理论与技术支撑。

[1]JinXiaoning,NiJun,KorenY.OptimalControlofReassemblywithVariableQualityReturnsinaProductRemanufacturingSystem[J].ManufacturingTechnology, 2011, 60(1):25-28.

[2]TangXifeng,MaoHaijun,LiXuhong.EffectofQualityUncertaintyofPartsonPerformanceofReprocessingSysteminRemanufacturingEnvironment[J].JournalofSoutheastUniversity(EnglishEdition), 2011, 27(1):92-95.

[3]苏春, 沙洋娟. 基于混合不确定性和证据理论的再制造生产计划[J].东南大学学报(自然科学版), 2010, 40(4):712-716.

SuChun,ShaYangjuan.RemanufacturingProductionPlanningBasedonMixed-uncertaintyandEvidenceTheory[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2010, 40(4):712-716.

[4]TeunterR,KaparisK,TangOu.Multi-productEconomicLotSchedulingProblemwithSeparateProductionLinesforManufacturingandRemanufacturing[J].EuropeanJournalofOperationalResearch, 2008,191:1241-1253.

[5]ZanoniS,SegerstedtA,TangOu,etal.Multi-productEconomicLotSchedulingProblemwithManufacturingandRemanufacturingUsingaBasicPeriodPolicy[J].Computers&IndustrialEngineering, 2012, 62(4):1025-1033.

[6]牛同训.再制造公差设计优化模型及其应用[J].计算机集成制造系统, 2011, 17(2):232-238.

NiuTongxun.OptimalModelforRemanufacturingToleranceDesignandItsApplication[J].ComputerIntegratedManufacturingSystems, 2011, 17(2):232-238.

[7]FergusonM,GuideVD,KocaE,etal.TheValueofQualityGradinginRemanufacturing[J].ProductionandOperationsManagementSociety, 2009, 18(3):300-314.

[8]ZhouJun,HuangPanling,ZhuYaguang,etal.AQualityEvaluationModelofReusePartsandItsManagementSystemDevelopmentforEnd-of-lifeWheelLoaders[J].JournalofCleanerProduction, 2012, 35:239-249.

[9]LiuMingzhou,LiuConghu,XingLingling,etal.StudyonaToleranceGradingAllocationMethodunderUncertaintyandQualityOrientedforRemanufacturedParts[J].Int.J.Adv.Manuf.Technol., 2013, 3:1-8.

[10]刘明周, 赵志彪, 凌先姣, 等. 基于最短路径的复杂机械产品装配过程质量控制点公差带在线优化方法[J].机械工程学报, 2012, 48(10):173-177.

LiuMingzhou,ZhaoZhibiao,LingXianjiao,etal.ResearchonOnlineToleranceOptimizationforComplexMechanicalProductsAssemblyProcessBasedonShortestPath[J].JournalofMechanicalEngineering,2012, 48(10):173-177.[11]刘明周, 任兰. 面向产品的制造质量控制模型研究[J].计算机集成制造系统, 2004, 10(7):764-768.LiuMingzhou,RenLan.ManufacturingQualityControlModelOrientedtoProduct[J].ComputerIntegratedManufacturingSystems, 2004, 10(7):764-768.

[12]雷英杰，张善文.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2005.

[13]冯定. 神经网络专家系统[M].北京：科学出版社,2006.

[14]张国庆，荆学东，浦耿强，等．汽车发动机可再制造性评价[J].中国机械工程,2005,16(8):739-742.

ZhangGuoqing,JingXuedong,PuGengqiang,etal.AssessmentonRemanufacturabilityoftheAutomobileEngines[J].ChinaMechanicalEngineering, 2005, 16(8): 739-742.

(编辑陈勇)

Online Tolerance Optimization for Remanufactured Complex Mechanical Product Assembly Processes

Liu MingzhouXing LinglingLiu ConghuZhang Miao

Hefei University of Technology,Hefei,230009

To improve the assembly precision of remanufactured complex mechanical products and the utilization ratio of remanufactured parts, an online tolerance optimization approach for remanufactured complex mechanical product assembly processes was put forward. First, the tolerance zone of the key process was divided into several zones with fine granularity based on the analysis of remanufactured complex mechanical product assembly characteristics. Second, under dimensional chain constraints, based on genetic algorithm an online tolerance optimization model was established with the minimum quality loss and comprehensive cost as target. Then a forward inference mode based on historical data and an backward inference mode based on the real-time assemble information were proposed respectively, which can dynamically deduce the optimal assembly scheme set guiding the remanufacturing assembly process and timely response to the abnormal. Finally, an online quality control prototype system for the remanufactured engine assembly in a power corporation remanufacturing assembly line was developed, which shows the feasibility and validity of the proposed strategy.

remanufacturing; assembly process; quality; online tolerance optimization

2013-07-25

国家重点基础研究发展计划(973计划)资助项目(2011CB013406)

TP315DOI：10.3969/j.issn.1004-132X.2015.01.010

刘明周，男，1968年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。主要研究方向为制造过程监测与控制、制造系统建模与仿真和CIMS等。邢玲玲(通信作者)，女，1989年生。合肥工业大学机械与汽车工程学院硕士研究生。刘从虎,男,1981年生。合肥工业大学机械与汽车工程学院博士研究生。张淼，男，1986年生。合肥工业大学机械与汽车工程学院博士研究生。