高频响测力仪固有频率的理论分析与试验

黄　震　赵　威

南京航空航天大学，南京，210016

高频响测力仪固有频率的理论分析与试验

黄震赵威

南京航空航天大学，南京，210016

针对现有测力仪固有频率较低而无法准确测量高转速下铣削力的难题，基于附加弹性测力原理设计了高频响测力仪，测力系统的固有频率达到9kHz以上，运用邓克莱法建立了测力仪的简化模型，推导出固有频率的解析式；进行了有限元仿真与模态试验，获得了测力仪固有频率的仿真值、实测值以及振型；最后进行了高转速铣削力验证试验。研究结果表明，该测力仪固有频率的解析值和仿真值略大于实测值，但三者较为接近，测力仪关键结构尺寸与其固有频率密切相关，利用简化模型和有限元法进行高频响测力仪的结构优化设计合理可行，为同类测力仪的结构优化设计提供了参考依据。

高频响测力仪；固有频率；有限元仿真；模态试验

0　引言

切削力是切削过程中重要的物理量之一，切削力对刀具磨损、切削温度、加工表面质量、系统振动等都有着直接的影响[1]。切削力信号的准确获取，对研究切削机理、加工工艺系统动态特性以及切削性能评价等至关重要。然而，在高转速、超高转速铣削加工过程中，工件受刀具多个切削刃周期性冲击、刀具磨损、材料变形以及切屑生成等因素的综合作用[2]，给切削力信号的准确测量带来了极大的困难。

目前切削力信号的主要获取方式是使用测力仪，常见的测力仪有电阻应变式测力仪[3-5]、压电式测力仪[6-7]、电感式测力仪[8]等，其中高转速下铣削力的测量一般采用高精度、高灵敏度以及大量程的商用压电式测力仪。然而，高速铣削时要求铣削力监测系统具有很高的分辨率和固有频率，从而精确地捕捉铣削力峰值，获得可靠的测量结果[9]。目前绝大部分测力仪的固有频率在1～5 kHz之间，且在安装刀具或工件后，测力仪的固有频率会进一步降低。

为了满足高转速、超高转速时的测力需求，本文基于附加弹性元件测力原理设计了应变式高频响测力仪，对其主要结构参数进行了优化，设计的高频响测力仪能够准确获取高转速、超高转速下铣削力信号。

1　测力仪主体结构与基本测力原理

图1所示为基于附加弹性元件测力原理[10]创新设计的高频响测力仪的主体结构，材料为铝合金Al-6061。其中，高刚度弹性柱体位于底座和上表面平台中间，每个附加弹性元件由2个中刚度弹性元件和1个低刚度弹性薄片组成，而4个附加弹性元件分别位于高刚度弹性柱体的四周[11]。高转速、超高转速铣削时，切削用量相对较小，同时由于测力仪自身尺寸的限制，试件的尺寸不宜过大。对于高频响测力仪，测试样件尺寸最好控制在20 mm×20 mm×4 mm范围内，主要采用粘贴方式(图1中试样粘贴区域)，由有限元仿真可知测力仪系统固有频率基本维持在10 kHz以上。若加工试件尺寸较大，可采用螺钉连接的方式，即在测力仪上表面四角加工M6对接内螺纹，但加工试件尺寸必须小于48 mm×48 mm×10 mm，否则测力仪与试件的整体固有频率会低于8.5 kHz，并且随着高度的增加，固有频率会有显著的降低。

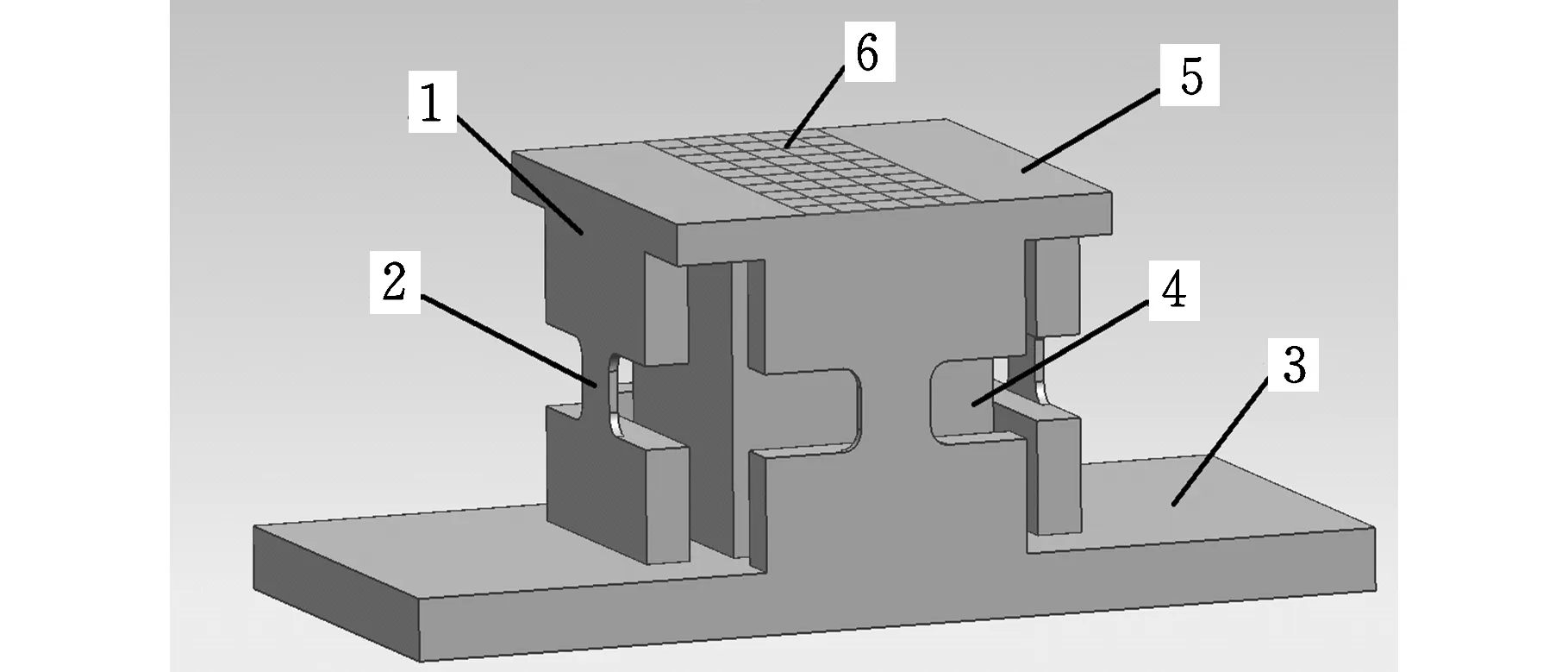
1.中刚度弹性柱体　2.低刚度弹性薄片　3.底座　4.高刚度弹性柱体　5.上表面平台　6.试样粘贴区域图1　测力仪的三维结构图

该测力仪主要针对扁长型的小型零部件，可测量其在高转速、超高转速铣削加工条件下的切削力，待加工材料主要采用胶水粘接的方式，试验表明，当材料粘结到测力仪上后，测力仪的固有频率不仅没有降低反而有所提高；若加工试件体积较大，可在测力仪上表面4个边角设计直径为6 mm的螺纹孔，采用螺栓连接的方式进行连接，同时材料的高度不能超过20 mm，且材料不能超过测力仪上表面，以保证测力精度。根据附加弹性元件测力原理，当测力仪上表面受力时，低刚度弹性薄片能够获取放大倍数明显的应变值，故将电阻应变片分别贴在低刚度弹性薄片表面，然后通过适当的电桥电路、应变放大仪以及NI数据采集卡获得电压信号，最后通过LabVIEW软件将电压信号转换为力信号，由此搭建一个完整的测力系统。

2　测力仪主体结构固有频率的理论计算

2.1测力仪主体结构固有频率的计算

根据测力仪的实体结构，将测力仪简化成图2所示的模型，其中，m4为上平台的质量，m5为底座的质量，k1、k2、k3分别为中刚度弹性厚片、低刚度弹性薄片、高刚度弹性柱体的刚度。根据振动系统求解固有频率近似方法中的邓柯莱法，若有n个耦合的自由度，则固有频率的近似公式为

(1)

其中，每一个频率ωii(i=1,2,…,n)是在略去系统中除各结构质量mi以外的所有质量之后计算得到的[12]。

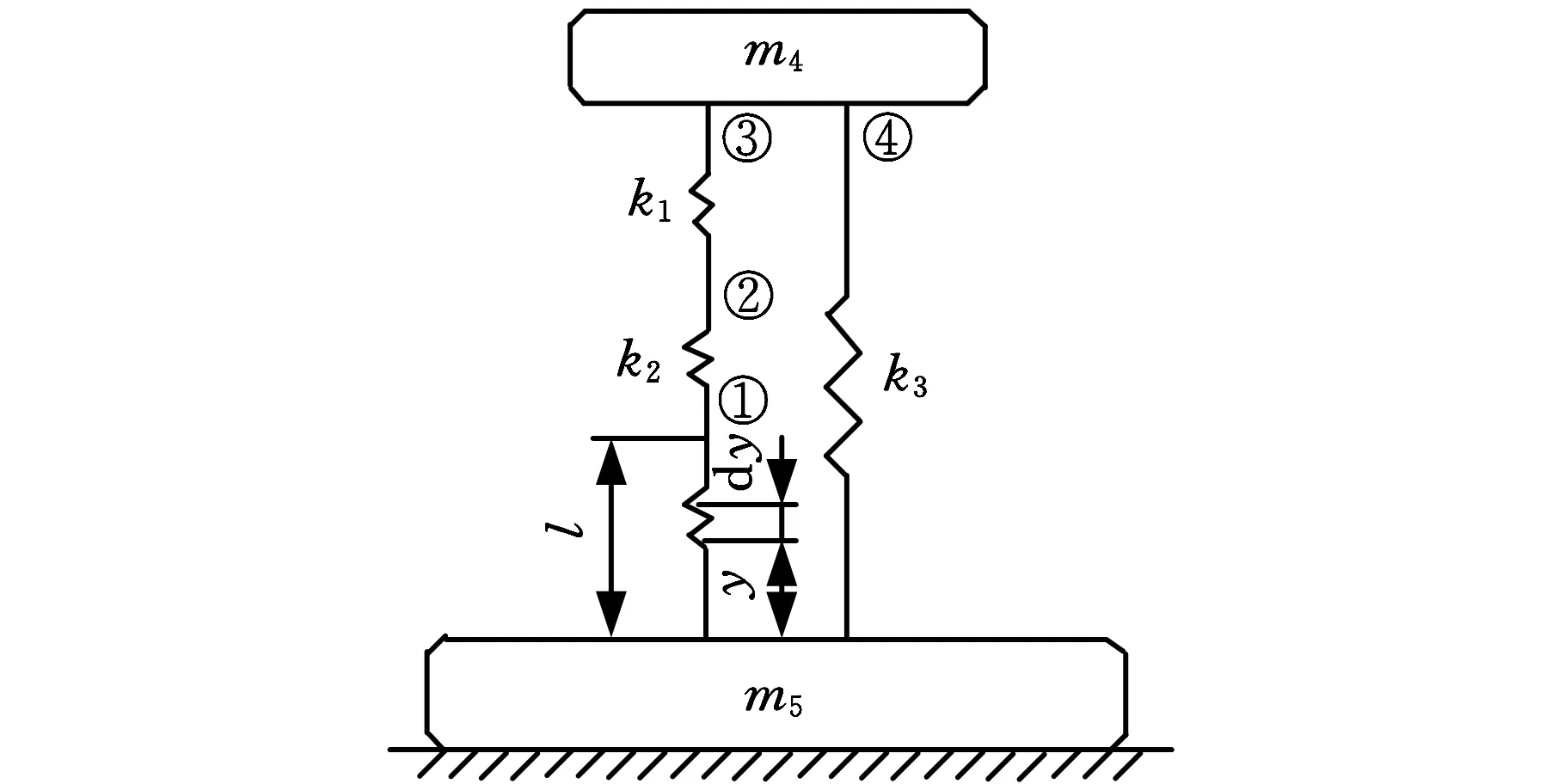
图2　测力仪的简化模型

对于该测力仪简化模型，可将其分为3个部分，其中ω1表示忽略上表面平台以及底座质量时整个测力仪平台振动的圆频率，ω4、ω5分别表示只考虑上表面平台和底座时整个测力仪平台振动的圆频率。由式(1)可知，整个测力仪自由振动时的圆频率为

(2)

K=1/(2/k1+1/k2)+k3

(3)

所以上表面平台的振动圆频率为

(4)

在忽略上表面平台以及底座质量的情况下，由于结构的复杂性和关联性，应用能量守恒定律对测力仪平台的自由振动进行研究。假设振动系统振动时的运动方程为

x=Asin(ω t+φ)

(5)

式中，x为距离；A为振幅；φ为相位。

则振动系统振动时最大动能和最大势能分别为

(6)

(7)

式中，meq为平均质量；keq为刚度平均值；qmax为速度的平方；ε0为角加速度。

由能量守恒定律可知

(8)

整个测力仪自由振动时最大动能和最大势能分别为

Ttmax=T1max+T2max+T3max+T4max

(9)

(10)

由式(5)可知

(11)

将式(9)～式(11)代入式(8)可得

(12)

式中，l1、l2、l3分别为中、低、高刚度弹性柱体长度；A1、A2、A3分别为中、低、高刚度弹性柱体横截面面积；E为材料弹性模量。

式(12)建立了测力仪固有频率与其所有结构尺寸之间的关系，通过式(12)可以获得固有频率的理论计算值，进行测力仪主体结构优化设计。

2.2测力仪主体结构固有频率的优化计算

基于式(12)，运用MATLAB软件对最终固有频率计算公式进行编程，获得测力仪固有频率与各尺寸的关系，见表1。综合考虑测力仪的量程范围(-1～1 kN)，低刚度弹性薄片的厚度不能小于0.7 mm，并且测力仪的主体结构轮廓尺寸在150 mm×60 mm×60 mm范围内，同时高刚度弹性柱体与附加弹性元件之间的距离必须在0.3～0.8 mm范围内，以保证应变放大倍数不低于11倍等因素，结合MATLAB软件对所得结果进行优化设计获得最终的尺寸(表1)，计算得到固有频率最终计算结果为ω=11 423 Hz。

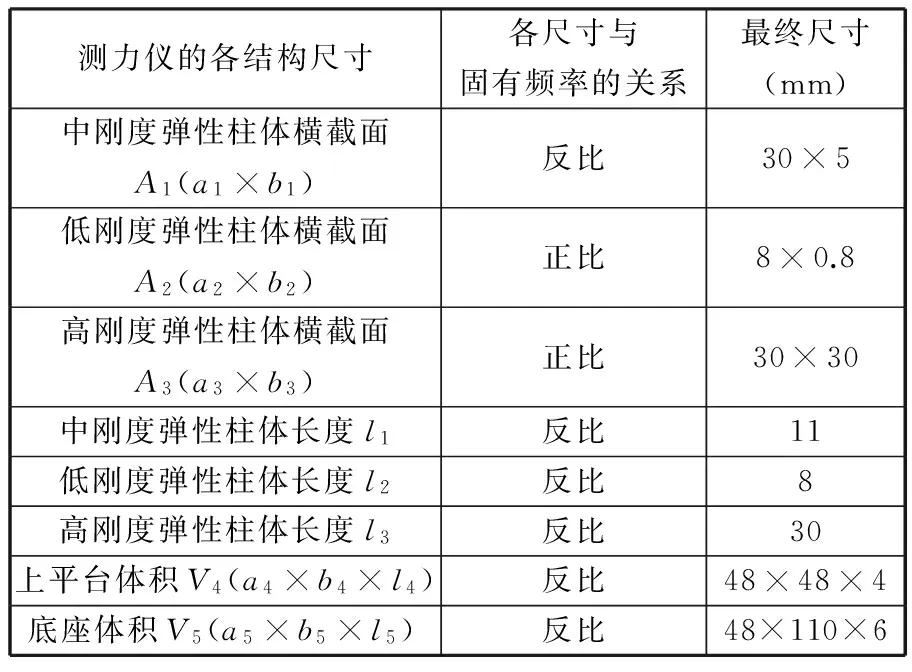
表1　测力仪的固有频率与各结构的尺寸关系及最终尺寸

3　基于ANSYS Workbench的有限元模态分析

3.1测力仪主体结构的建模

基于ANSYS Workbench软件对测力仪主体结构进行模态分析，在UG中将建好的几何模型转换为IGES格式文件，然后直接导入ANSYS Workbench。在modal模块中选择Refinement命令对低刚度弹性薄片进行网格局部单元细化处理，设网格单元尺寸为0.1 mm，测力仪主体结构其他部分的网格划分采用四面体网格自动生成。对测力仪主体结构进行模态分析时，约束条件设置为底座上下表面固定，与实际加工工况相符。

3.2有限元模态结果分析

图3为高频响测力仪的一阶振型图，其第一阶振型表现为X方向两块低刚度弹性薄片带动测力仪整体在X方向产生一阶弯曲，导致测力仪的上表面平台沿X方向有明显的高低差异，此时得到测力仪的固有频率为10 433 Hz。同时借助有限元仿真求得不同低刚度弹性柱体长度l2对应的测力仪的固有频率，其变化趋势如图4所示，随着l2的增大，测力仪的固有频率呈现出下降的趋势，仿真结果与表1相吻合，而针对其他结构尺寸的有限元仿真也与理论计算一致，从而验证了测力仪理论计算模型的正确性。

图3　高频响测力仪的第一阶振型

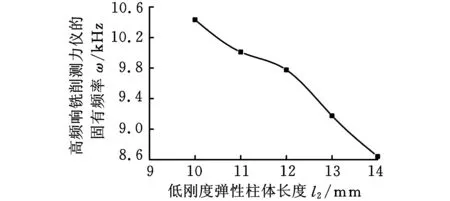
图4　不同l2对应的测力仪的固有频率

4　测力仪振动模态试验及高转速铣削力试验

4.1测力仪的振动模态验证试验与分析

将测力仪安装到机床平台上，采用压板压紧的装夹方式，利用锤击法对测力仪进行振动模态试验及分析，以检验测力仪简化模型及有限元仿真的准确性。模态试验前，在测力仪的上平台划分4×4网格，网格节点为力锤敲击点，在低刚度弹性薄片表面贴上加速度传感器。试验时分别敲击每个点，并取10次平均值，通过Agilent35670a频谱分析仪获得频响函数。

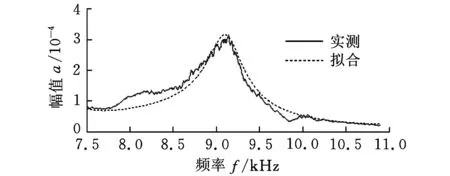
(a)测力仪的振动幅值图

(b)测力仪的振动相位图图5　模态试验所得测力仪的幅值图和相位图

采用MATLAB软件对所测点的频响函数进行编程，利用有理分式法识别出该阶模态的固有频率以及该测点的振型系数，并绘制出该阶模态的振型图[13]。实测和拟合出的幅频图和相频图如图5所示。由图5可知，幅值和相位变化较为吻合，辨识出测力仪的固有频率为9106 Hz。模态试验测试所得的固有频率值比理论计算和有限元仿真所得结果都要低。主要原因是理论计算和有限元仿真都属于模拟计算，没有充分考虑实际工况。图6所示为振动模态试验所得测力仪的振型，包含初始上表面和振动后的上表面，通过比较第一阶振型上表面的变化可知，有限元计算出的振型图与试验所得振型图基本一致，均是由薄壁件弯曲振动，带动平台向弯曲方向移动，使平台表面产生高低差异。试验结果验证了有限元仿真的可靠性，为利用有限元仿真对测力仪进行优化设计提供了试验依据。

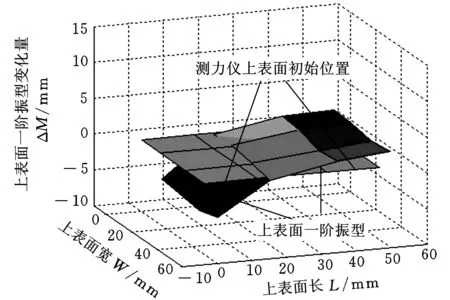
图6　振动模态试验所得振型图

4.2高转速铣削力试验及分析

为了检验该测力仪的效果，将该测力仪主体结构与加工试验件等连接，构建成完整的测力系统，并在静态标定以及修正矩阵的计算之后，进行高转速铣削力试验。其中，试样为铝合金Al-6061，尺寸为20 mm×20 mm×4 mm，试验时将该试样粘在测力仪上表面，由于其尺寸相对较小，与测力仪主体结构固连后基本不改变测力仪的固有频率(固连后的测力系统有限元仿真所得固有频率为100 79 Hz)。数控机床为Caver400M-RT，其转速范围为10 000～42 000 r/min，最大工作进给速度为12 m/min，如图7所示。刀具为涂层硬质合金立铣刀，其直径为3 mm，齿数为2，螺旋角为30°。铣削方式为顺铣干切削，转速为4×104r/min，每齿进给量为0.02 mm，轴向切深为0.5 mm，径向切深为0.5 mm。

图7　Caver400M_RT雕刻机

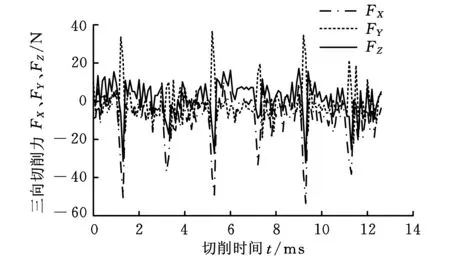
图8　40 000 r/min转速下切削力数据图

图8所示为该测力仪在机床主轴4×104r/min转速下获得的切削力数据。三向切削力呈现出明显的周期性变化，表明该测力仪所获得的的切削力数据能够准确反映高转速条件下切削力的基本特征。其中，由于X方向进给抗力最大，故FX的幅值明显大于FY、FZ。此外，铣刀的两个刀齿存在微量的动不平衡，导致刀齿的实际切深不同，所以相邻的两个波峰有次序地高低相间。

5　结论

(1)本文建立了高频响测力仪的理论模型，并且求得了固有频率的解析模型，实现了结构尺寸的优化，并进行了有限元仿真验证。

(2)模态试验和有限元仿真的振型基本一致，均是由两侧薄壁件弯曲振动，带动平台向弯曲方向移动，使平台表面产生高低差异，验证了有限元仿真的可靠性，为测力仪的优化设计提供了参考依据。

(3)高频响测力仪在高转速铣削试验时能够获得清晰的三向铣削力周期信号，表明测力仪的固有频率能够满足高转速铣削的要求，验证了该测力仪结构设计的可行性。

[1]Schulz H, Abele E, 何宁. 高速加工理论与应用[M]. 北京: 科学出版社, 2010.

[2]仇健, 李晓飞, 马晓波,等. 硬质合金立铣刀高速铣削铝合金切削力实验研究[J].中国机械工程, 2011, 23(13): 1555-1560.

Qiu Jian, Li Xiaofei, Ma Xiaobo,et al. Experimental Study of Cutting Forces on High Speed Milling Aluminum Alloy Using Carbide End Mill[J].China Mechanical Engineering, 2011,23(13):1555-1560.

[3]Korkut I.A Dynamometer Design and Its Construction for Milling Operation[J]. Materials and Design, 2003, 24(8):631-637.

[4]Karabay S.Design Criteria for Electro-mechanical Transducers and Arrangement for Measurement of Strains due to Metal Cutting Forces Acting on Dynamometers[J].Materials and Design, 2007,28(2):496-506.

[6]Castro L R, Viéville P,Lipinski P.Correction of Dynamic Effects on Force Measurements Made with Piezoelectric Dynamometers[J].International Journal of Machine Tools & Manufacture, 2006, 46(14): 1707-1715.

[7]Transchel R, Stirnimann J, Blattner M, et al.Effective Dynamometer for Measuring High Dynamic Process Force Signals in Micro Machining Operations[C]//5th CIRP Conference on High Performance Cutting.Zurich,2012: 558-562.

[8]Albrecht A, Park S S, Altintas Y, et al.High Frequency Bandwidth Cutting Force Measurement in Milling Using Capacitance Displacement Sensors[J].International Journal of Machine Tools & Manufacture, 2005, 45(9): 993-1008.

[9]刘战强, 万熠, 艾兴. 高速铣削中切削力的研究[J].中国机械工程, 2003, 14(9): 734-737.

Liu Zhanqiang, Wan Yi, Ai Xing.Cutting Forces in High Speed Milling[J].China Mechanical Engineering, 2003, 14(9):734-737.

[10]金问林, 张幼桢, 褚涛.切削测力仪的杠杆—附加弹性元件设计方法[J].南京航空航天大学学报, 1991, 23(3): 33-37.

Jin Wenlin, Zhang Youzhen, Chu Tao. Parasitic Elastic Element Method for Cutting Dynamometer Design[J]. Journal of Nanjing Aeronautical Institude,1991,23(3):33-37.

[11]孙永华, 赵威, 何宁，等. 高频响三维动态铣削力测试平台设计[J].南京航空航天大学学报, 2012, 44(4): 154-156.

Sun Yonghua，Zhao Wei，He Ning，et al. Design of High Frequency Three-dimensional Dynamic Milling Force Test Platform[J].Journal of Nanjing University of Aeronautics &Astronautics, 2012, 44(4):154-156.

[12]Szuladzinski G.机械与结构动力学[M].北京:机械工业出版社,1985.

[13]Totis G, Wirtz G, Sortino M,et al. Development of a Dynamometer for Measuring Individualcutting Edge Forces in Face Milling[J].Mechanical Systems and Signal Processing, 2010, 24(6): 1844-1857.

(编辑陈勇)

Theoretical Calculation and Experimental Analyses of Natural Frequency for High Frequency Dynamometer

Huang ZhenZhao Wei

Nanjing University of Aeronautics & Astronautics,Nanjing,210016

Concerning the low natural frequency of dynamometers for high speed cutting to acquire forces signals, a initial model of high frequency dynamometer was designed and its natural frequency can be as 9 kHz. Based on the method of Dunkerley, a simplified model of the dynamometer was built to achieve the theoretical natural frequency and the computational formula.Meanwhile, the simulation values and actual values of the natural frequency were obtained by modal analysis with the use of the finite element simulation and vibration modal test, and the high speed cutting test was conducted for the validation. The results indicate that theoretical values and simulation values are a little greater than the actual values, and the dimensions of key structure have an great impact on the natural frequency, which provide a necessary reference for the structure optimization of similar dynamometers.

high frequency dynamometer;natural frequency; finite simulation; modal test

2013-09-25

国家重点基础研究发展计划(973计划)资助项目(2009CB724401)

TG501.3< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.01.002

黄震，男，1989年生。南京航空航天大学机电学院硕士研究生。主要研究方向为精密仪器。赵威(通信作者)，男，1977年生。南京航空航天大学机电学院副教授。