PISA测试对我国中职数学习题设置的启示

李雅琪

【摘要】《上海市中等职业学校数学课程标准》（2015修订稿）中强调“中等职业学校数学课程应加强贴近学生生活实际和所学专业相关的数学应用意识。”为此，本文借鉴PISA测试题目中问题情境的分类，对中职数学习题的设计作一些尝试，以期对我国中职学生数学核心素养的养成发挥一点益处，增添一抹色彩。

【关键词】国际学生评价项目（PISA） 中职数学习题 情境创设

【中图分类号】G71 【文献标识码】A 【文章编号】2095-3089（2015）10-0158-02

一、问题的提出

众所周知，数学学科具有高度的抽象性。对于大部分中职学生来讲，数学基础又较为薄弱，再加上自身良好学习习惯的未加养成，诸多因素导致他们感觉数学学习既枯燥又繁难，学习数学无任何兴趣和积极性，厌学情绪的逐日增长令人堪忧。我们经常会听到学生的抱怨声“老师，我们学这么复杂的数学有什么用啊！？”的确，在中职校，其中相当一部分学生以就业为主，如果他们每日接触的数学练习多为没有实际背景的纯理论性题目，这在一定程度上脱离了他们的生活实际，其学习结果可想而知。

如何让我们的学生多掌握一些他们所必须的数学知识，提高一点解决实际问题的能力，成为我们不得不面对的现实和亟待解决的问题。本文试图借鉴PISA测试，从习题设置的角度作一些尝试，以期对我国中职学生的数学学习能够起到积极的作用。

二、理论依据

（一）《上海市中等职业学校数学课程标准》

《上海市中等职业学校数学课程标准》（2015修订稿）（以下简称《标准》）中指出：“中职数学核心素养主要包括‘数学知识、‘数学文化、‘数学意识、‘数学能力四部分。”其中“数学文化”提到学生要能够“认识到数学与未来生活的联系”；“数学意识”表现为学生拥有“用数学眼光看世界的理念”；而“数学能力”需要学生“在与数学相关的问题解决过程中形成”。《标准》特别强调了“中等职业学校数学课程应摒弃不必要的繁杂运算与高难度的解题技巧，……，要加强贴近学生生活实际和所学专业相关的数学应用意识。”

（二）弗赖登塔尔（H.Freudenthal）的现实数学教育理论

现实数学教育是指由弗赖登塔尔领衔的荷兰数学教育研究集体在20世纪近半个世纪的时间里丰富、发展和完善起来的新型数学教育。现实数学教育有这样一个基本特征：现实数学教育是现实的，即现实数学教育与学生熟悉的生活密切相关，学生通过自己熟悉的生活学习数学，作为教育内容的数学和现实生活中的数学始终紧密的联系在一起。[1]

（三）建构主义学习理论

建构主义学习理论认为，“学习是获取知识的过程，但知识不是通过教师传授得到，而是学习者在一定的情境即社会文化背景下，借助其他人（包括教师和学习伙伴）的帮助，利用必要的学习资料，通过意义建构的方式而获得”，“学习是学生主动的建构活动，学习应与一定的情境相联系，在实际情境下进行学习，可以使学生利用原有知识和经验同化当前要学习的新知识。这样获取的知识，不但便于保持，而且容易迁移到新的问题情境中去。”[2]从中我们可以看出，在建构主义理论下，实际情境在学生的学习当中是一个很重要的要素。

三、PISA测试题目对情境类型的划分

PISA（Programme for International Students Assessment）是一项由经济合作与发展组织的国际性学生评价项目，主要评价大约15周岁学生的阅读、数学与科学素养水平，检测他们是否具备了未来生活所需的知识与技能，以及在现实生活中运用这些知识和技能解决问题的能力。

根据情境创设的角度的不同，创设情境的类型也呈多样化的特点，并不拘泥于一格。PISA在其框架（2006）中指出：“学生在解决问题时，数学方法和表征方式的选择取决于具体问题所处的特定情境。这种特定情境是学生面临的任务的一个组成部分。运用于问题解决的四种情境（按照与学生关系的密切程度）依次是：以个人生活为背景的情境、以学校、工作或者娱乐休闲生活为背景的情境、发生在当地社团或者社会日常生活中的情境，最后一种则是以科学知识为背景创设的情境。”[3]

同时该框架把这四种类型的情境概括为四类：个人类的（Personal）、教育或者職业类的（Educational/Occupational）、公共类的（Public）以及科学类的（Scientific）情境。[3]从PISA对情境的这些分类，我们可以看出与“科学类情境”不同，其前三种类型的情境主要是围绕现实生活所做的划分。篇幅所限，本文习题设置主要围绕前三类情境展开。

四、借鉴PISA尝试设置中职数学习题

的确，通过挖掘现实生活中的各种素材，从中提取一些与数学知识相关的问题，对于培养学生学习数学的兴趣以及提高运用数学的思维方式观察、分析、解决现实社会中的各种相关问题的能力可以起到积极的作用。本文习题中涉及的情境元素，基本上借鉴PISA对情境类型的划分，具体设置如下：

（一）个人类情境（Personal Situation Type）

现实生活中有大量的信息与数学乃至几何有着千丝万缕的联系。而正如上述PISA所指出的，与学生关系最密切的即是其个人生活。

体重是反映和衡量一个人健康状况的重要标志之一。世界卫生组织推荐的计算体重的方法：男性：（身高CM-80）×70%=标准体重（kg），标准体重正负10%为正常体重。网络班的男同学小夏的身高为180CM，则他的标准体重应为（180-80）×10%=70（kg），其正常体重的范围为63≤x≤77。那么，该体重范围可用绝对值不等式表示为（ ）。

A.|x-70|≥7 B.|x-7|≤70

C.|x-70|≤7 D.|x-7|≥70

上述问题中的情境围绕学生生活而设计，并巧妙地将“绝对值不等式”的知识融入其中。

（二）教育类或者职业类情境（Educational or Occupational Situation Type）

如前所述，PISA（2006）将在学校生活中发生的情境定义为“教育类情境”。

1.为了丰富同学们的业余生活，提高全校师生的身体素质，某中职校每年举行一届体育节活动。小王同学打算参加今年的3000米长跑项目，他为自己制定了如下训练计划：第一天跑步300米，以后每天跑的长度都比前一天增加10%。

（1）写出他每日跑步的里程数所构成的数列的通项公式；

（2）他要经过多少天的训练，可以达到单日跑步里程3000米？

（3）计算小王同学从训练开始的20天内所跑里程的总数。（结果保留到整数）

2.小李是某室内设计公司的助理设计师，目前他的底薪是每月2500元。公司规定，每月他为设计师绘制第一套方案图提成300元，以后依次以50元递增，小李在上月共拿到薪酬5050元。那么：

（1）若把某月内每套方案图的提成记为数列{an}，请写出数列{an}的通项公式；

（2）小李在上月共绘制了多少套方案图？

（3）若适逢行业旺季，小李在一个月内绘制套方案图总共可以拿到多少提成？

结合校园生活并加强职业的元素，很贴合我们中职生的学习实际。上述两个问题即是迎合了这样的设计理念，让学生能真正感受得到数学就在他们身边。

（三）公共类情境（Public Situation Type）

虽然与学生关系最密切的是其个人生活中发生的各类事件，但对于中职校的学生来讲，他们对于公共生活中的一些事物已经有一定的耳闻和了解，故而有必要把素材选择的范围从学生的个人生活和学校生活扩大到对公共生活中去，拓宽学生的视野。

本文将此类情境又分为天文、建筑与地理、医药、新闻以及社会生活等方面，具体如下：

1.天文

二十四节气表是我国古代订立的一种用来指导农事的补充历法，它是根据太阳在黄道（即地球绕太阳公转的轨道）上的位置来划分的。古人把太阳黄经的360°分成24等分，每份15°为一个节气。按照天文学惯例，以春分点为起点（0°）自西向东度量。若把每一节气所对应的黄经度数所成的数列记为{an}，春分a1=0，清明a2=15，…，惊蛰a24=345。

（1）写出数列{an}的通项公式；（1≤n≤24，n∈N*）

（2）计算节气“处暑”所对应的黄经度数。

（附二十四节气：立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种、夏至、小暑、大暑、立秋、处暑、寒露、秋分、寒露、霜降、立冬、小雪、大雪、冬至、小寒、大寒。）

2.医药

一位病人在早上8点口服一粒1000mg的药片，若每隔一小时，残留在他体内的药物减少到前一小时的75%。把药物每小时结束时残留在病人体内的剂量排成的数列记为{an}，则a1=1000×75%。

（1）写出数列{an}的通项公式；

（2）中午12点的时候，药物在病人的体内还残留多少？（保留到整数）

（3）几小时之后，药物在病人体内的残留量约为1mg？

3.新闻

（摘自2015年02月05日新闻网）河北一名村支书自掏220多万元给全村2880名村民每人分发带鱼、大米、面粉、花生油等12种年货，并且给予60岁以上的老人还额外发放生活补助金，具体标准是：60-69岁1200元，70-79岁1800元，80-89岁2400元，90岁以上3000元。

（1）写出该村支书为60岁以上的老人发放生活补助金依次排成的数列；

（2）判断该数列是否为等差数列，若是，请写出其公差；

（3）画出上述数列的图像。

4.建筑与地理

圜丘坛建于我国明朝，在天坛的南部。如图（一）所示，坛为三层露天圆台，每层圆台台面都铺了9圈扇形石，共27圈，且每圈的扇形石都比里面一圈多9块。在第一层圆台中央镶嵌一块圆形石板，叫“天心石”。把每一圈的扇形石数组成数列{an}，围绕天心石所铺的第一圈扇形石数记为a1=9，第二圈a2=18，第三圈a3=27，…，依此类推。

（1）写出数列{an}的通项公式，并求出第27圈扇形石数；

（2）求出这27圈扇形石的总数。

5.社会生活

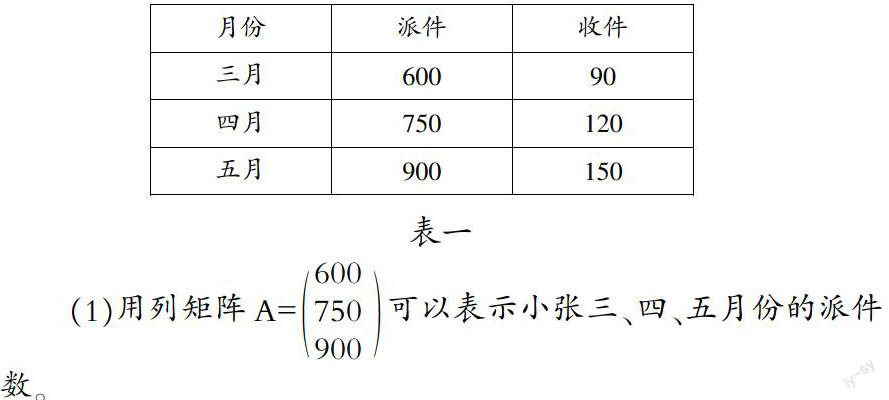
某快递公司快递员小张在三、四、五月份的派、收件单数如表一。公司规定每单派件提成2元，每单收件提成3元。

表一

（1）用列矩阵A=600750900可以表示小张三、四、五月份的派件数。

请用列矩阵B表示他在三、四、五月份的收件单数。 （表一）

（2）试用矩阵计算小张分别在这三个月中派、收件的提成总额。

（3）小张预计在六月份能派件900单，要想使得派、收件的提成总额达到3000元，那么，他在六月份至少要收件多少单？请通过计算说明理由。

总之，在中职生的数学学习中融入各类现实情境，让数学也能在孩子们的眼中变得更容易接受，更亲近一些，值得我们深入探讨。本文的习题设置大多围绕“数列”部分，期待后续有其它内容的研究不断呈现。

参考文献：

[1]孙晓天. 数学课程发展的国际视野[M]. 北京： 高等教育出版社， 2003.

[2]袁振国主编.当代教育学[M].北京：科学教育出版社，2004.

[3]Programme for International Student Assessment. Assessing Scientific， Reading and Mathematical Literacy： A Framework for PISA 2006. OECD Publishing， 2006.

[4]上海市教育委員会.《上海市中等职业学校数学课程标准》[S].上海：华东师范大学出版社，2015.

[5]陈慧，袁珠.PISA：一个国际性的学生评价项目[J].外国中小学教育，2008（8）：53-58.