一种基于嵌入技术的异构信息网络的快速聚类算法
陈丽敏 杨 静 张健沛
一种基于嵌入技术的异构信息网络的快速聚类算法
陈丽敏*①②杨 静①张健沛①
①(哈尔滨工程大学计算机科学与技术学院 哈尔滨 150001)②(牡丹江师范学院计算机系 牡丹江 157012)
异构信息网络聚类分析是当前的热点研究问题之一。利用异构信息网络的稀疏性,该文提出一种基于嵌入技术的星型模式的异构信息网络的快速聚类算法。首先从相容的角度将异构信息网络转化为若干个相容的二部图,使用随机映射和一种线性时间求解程序快速计算出每个二部图的近似通勤距离嵌入,每个嵌入都存在一个子集指示目标数据集;然后,使用这些指示子集构建一个通用的聚类模型;最后,将所有指示子集的类设置标号,通过计算指示同一目标对象的指示数据与标号相同类的中心点的加权距离总和,同时划分所有的指示子集,从而快速获得通用模型的极小值。通过理论分析及实验验证,该文算法聚类速度快,聚类准确率高。
异构信息网络;聚类;通勤距离;嵌入;加权距离总和
1 引言
信息网络普遍存在,如社会信息网络、DBLP书目网络等。同构信息网络是由一种类型数据构成的,异构信息网络则是由多种类型数据构成的。目前,同构信息网络的聚类研究已经非常丰富[1,2],但异构信息网络的聚类研究还不多,而异构信息网络聚类分析能更好地理解网络的隐藏结构以及每个类中的数据所代表的角色[3,4]。
异构信息网络中,星型网络模式非常流行,也非常重要。星型网络模式由一个目标对象数据集和多个属性对象数据集构成,关系只存在于目标对象与属性对象之间,属性对象之间不存在关系。
基于相容二部图的思想解决多种异构数据之间的复杂关系是行之有效的,从相容的角度出发,人们先后设计了多种算法解决了多种异构数据协同聚类的问题,其中比较经典的算法有基于半正定的规划算法[5],基于信息论的算法[6]以及谱聚类算法[7]。这类算法比较通用,但对于异构信息网络而言这些算法的复杂度太高。
基于概率模型的异构信息网络聚类算法NetClus[8]虽然聚类效率较高,但不具有通用性,而且算法的收敛性也不是很稳定,基于概率模型的思想还被用于网络服务聚类[9,10]。ComClus[11]算法是NetClus的衍生算法,面向包含同构关系与异构关系的信息网络,仍然离不开具体的应用领域,不具有通用性。基于密度的异构网络的子空间聚类算法计算速度较慢[12],使用语义路径相似性与传统算法结合的异构网络聚类[13,14]也与具体应用领域相关。
异构网络链接推理[15]时,往往需要最初的聚类划分更精确一些,因此高准确率的聚类是十分必要的,但是当网络的数据量非常大时,计算速度又不能太慢。文献[16]在同构数据上使用近似通勤距离嵌入聚类取得了非常好的效果。星型网络模式的异构信息网络能够转换成若干个相容的二部图,使用通勤距离度量二部图各结点之间的关系,能够提高聚类准确率。异构信息网络规模大,但是很稀疏,所以可以使用随机映射和线性时间求解程序[17,18]快速计算出每个二部图的近似通勤距离嵌入。每个嵌入都存在一个子集指示目标数据集,使用这些指示子集构建一个通用的聚类模型。然后将所有指示子集的类设置标号,通过计算每个目标对象的所有指示数据与标号相同的类的中心点的加权距离总和,同时划分所有的指示子集,从而快速获得该通用模型的极小值。本文算法是一个通用的异构信息网络聚类算法,计算速度快,聚类准确率高。
2 二部图的近似通勤距离嵌入
2.1 二部图的通勤距离嵌入
是二部图G的权重总和,即,是第个元素为1的单位列向量,即

设二部图G有条边,根据文献[20],定向G的边,令

其中,是G的任意两个结点,则是一个有向边-点入射矩阵。设是由边的权值构成的对角矩阵,则G的Laplace矩阵可表示为。
由性质1,G的任意两个结点,的通勤距离c为
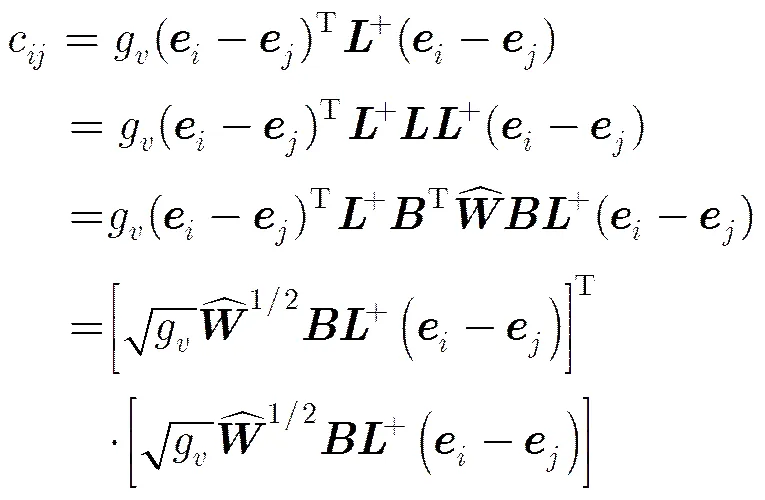
则c是空间第个列向量与第个列向量的欧式距离的平方,称为二部图G的通勤距离嵌入。是G的两个结点间的平均路径长度,而不是两结点间的最短路径,因此使用通勤距离度量结点间的关系,能够捕获复杂的类,聚类有噪音的数据,鲁棒性更好。那么,使用通勤距离嵌入聚类也能够捕获复杂的类。
2.2二部图的近似通勤距离嵌入
引理1[21]给定向量和,是行向量独立同分布的随机矩阵,其中等概率,。则,至少存在概率满足
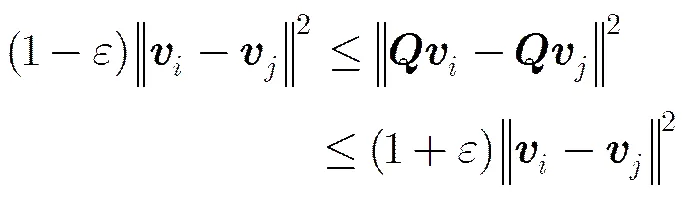
定理1 给定二部图G,,矩阵, 则,至少存在概率满足
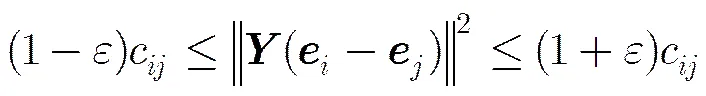
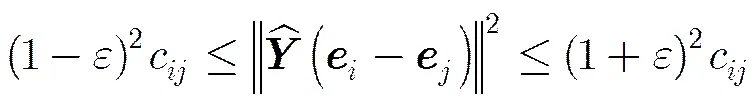
似通勤距离嵌入,二部图的近似通勤距离嵌入(Approximate Commute Distance Embedding of bipartite graph, ACDE)算法如表1所示。
表1二部图的近似通勤距离嵌入

0与1的数据对象映射到了一个共同的子空间。的前0个列向量指示数据集0,后1个列向量指示数据集1。稀疏矩阵有个非零元素,第(1)步计算与及的时间复杂度为。因为稀疏矩阵有2个非零元素,对角矩阵有个非零元素,故第(2)步计算的时间复杂度为。使用STSolve方法[17,18]计算方程组的一个解需要花费时间,故第(3)步构造的时间为。则算法ACDE的时间复杂度为++=。后续实验证明,在不同的数据集上k取值都很小。
3 基于近似通勤距离嵌入的异构信息网络聚类
3.1通用模型的构建
目标数据集0与属性数据集构成一个二部图,一个二部图对应一个关系矩阵。由算法ACDE计算二部图的近似通勤距离嵌入,其中的前0个数据指示目标数据集0,表示为,后n个数据指示属性数据集X,表示为,称与为指示子集。指示0的第个对象,称为指示数据,。的指示数据与0的对象一一对应。包含个二部图,个二部图对应个近似通勤距离嵌入,则目标数据集0被个指示子集所指示,0的每个对象被个指示数据所指示。
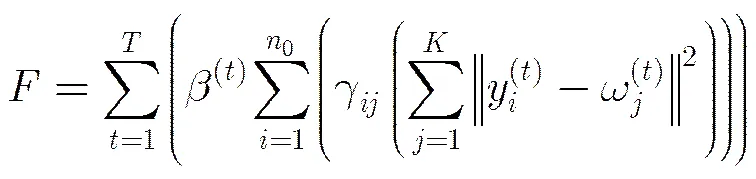
从相容的角度,式(1)目标函数取得最小值,则目标数据集0聚类达到最佳。显然,式(1)的全局最优解是NP难问题。
3.2 快速算法的推理
3.2.2加权距离总和0的一个对象被个指示数据所指示,这个指示数据到各自嵌入子集的类的中心点的距离都影响着该目标对象所属类的分配。指示数据到中心点的距离的权重由其指示子集的权重决定,指示子集的权重就是相应的关系矩阵的权重。

3.2.3的极小值求解可以进一步表示为
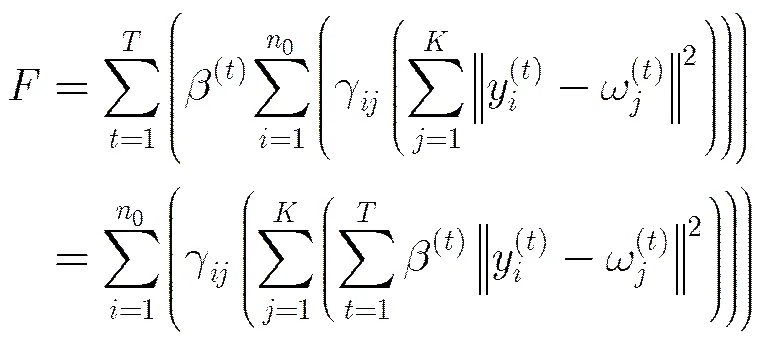
定理2

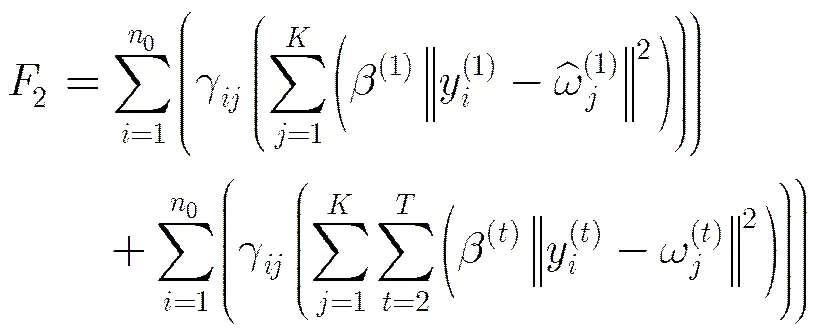
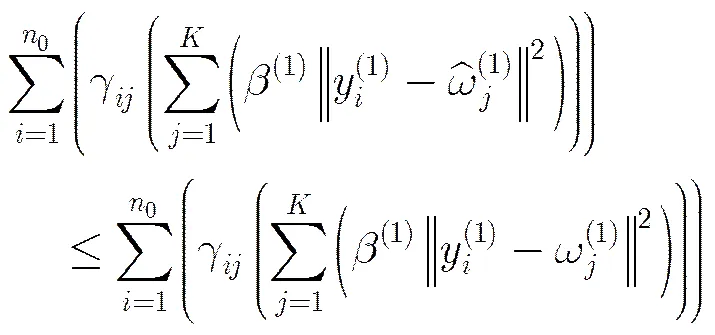
表2基于嵌入技术的异构信息网络快速聚类算法

由算法1的时间复杂度分析可知算法2第(1)步的时间复杂度为,其中是异构信息网络的二部图的数目,k是指示子集数据的维度,n与s是第个二部图的结点数与边数。第(2)步仅仅花费()时间,是常量。第(3)步花费(uTKkn0)时间,其中是聚类数目,0是0的对象数目,是式(3)收敛的迭代次数。所以算法FCAET的时间复杂度为+(uTKkn0),其中k,都很小,而与是常量。
4 实验
4.1 实验数据
从DBLP选取真实数据建立实验数据集,DBLP是一个典型的异构信息网络,其中包括4种类型数据对象,分别命名为papers, authors, terms和venues。首先抽取一个小数据集S1,即文献[8]使用的称为“four-area dataset”的数据集。小数据集S1选取了4个学术区域,这4个区域为:database, data mining, information retrieval及machine learning。每个区域取5个有代表性的会议,共20个会议,20个会议的所有authors, papers及出现在论文题目中的所有terms。
本文又抽取2008~2012年的8个学术区域的DBLP数据作为另外一个测试数据集,这8个学术区域为:databases, data mining & machine learning, information retrieval, computer graphics, computer network, information security, computer architecture, software engineering & programming language。数据集共包括80个venues(每个区域选取10个venues), 21,271个papers, 45, 576个authors及42, 962个terms。这个大的数据集称为S2。
当分析papers时,papers作为目标数据集,其他为属性数据集。因为DBLP提供了非常有限的引用信息,故papers之间不设置直接的链接。当分析authors时, authors 作为目标数据集,papers 与venues 作为属性数据集。由于合作关系,authors之间存在直接的链接。故authors还作为目标数据集的另外一个属性数据集。
本文算法均采用文献[22]的一种近乎线性时间的求解程序计算算法中的嵌入数据集,该方法用于对角占优矩阵,网址http://www.cs.cmu.edu/~ jkoutis/cmg.html。实验的运行环境为Inter Pentium III处理器,2 GB内存,Windows XP操作系统,Matlab编程。
4.2 关系矩阵的确定
当papers为目标数据集, authors, venues 和terms 为属性数据集。0表示目标数据集papers,1,2与3分别表示属性数据集authors, venues与terms。0与的关系矩阵为,其中的元素为

当authors为目标数据集, papers 和 venues 为属性数据集。因为作者之间存在合作关系,authors也是另外一个属性数据集。0表示authors,1与2分别表示papers与venues。为0与X的关系矩阵,。其中的元素为

实验的所有算法均采用相同的关系矩阵。
4.3 参数分析
4.3.1参数k分析k在不同的数据集上取值都非常小[16]。文献[16]实验证明对同构数据集,当时,准确率曲线已经很平滑。取小数据集S1来比较参数k的变化对异构信息网络数据聚类准确率的影响。使用算法FCAET聚类papers时,的权重分别取,,。聚类authors时,的权重分别取,,。迭代次数。k对算法准确率的影响如图1,图2所示。
实验说明当k>50时准确率曲线已经趋于平滑。因此取k=60是很适合的。k很小,且对算法FCAET的计算速度基本没有影响。这也是算法FCAET的一个优点,即在准确性方面对参数k不敏感。其他实验也取相同的关系矩阵权重及k=60。
4.3.2 迭代次数分析 取小数据集S1比较迭代次数对异构信息网络数据聚类准确率的影响。迭代参数对papers及authors聚类准确率的影响如图3,图4所示。当时,算法就已经收敛,说明本文算法收敛速度非常快,本文其他实验均取。
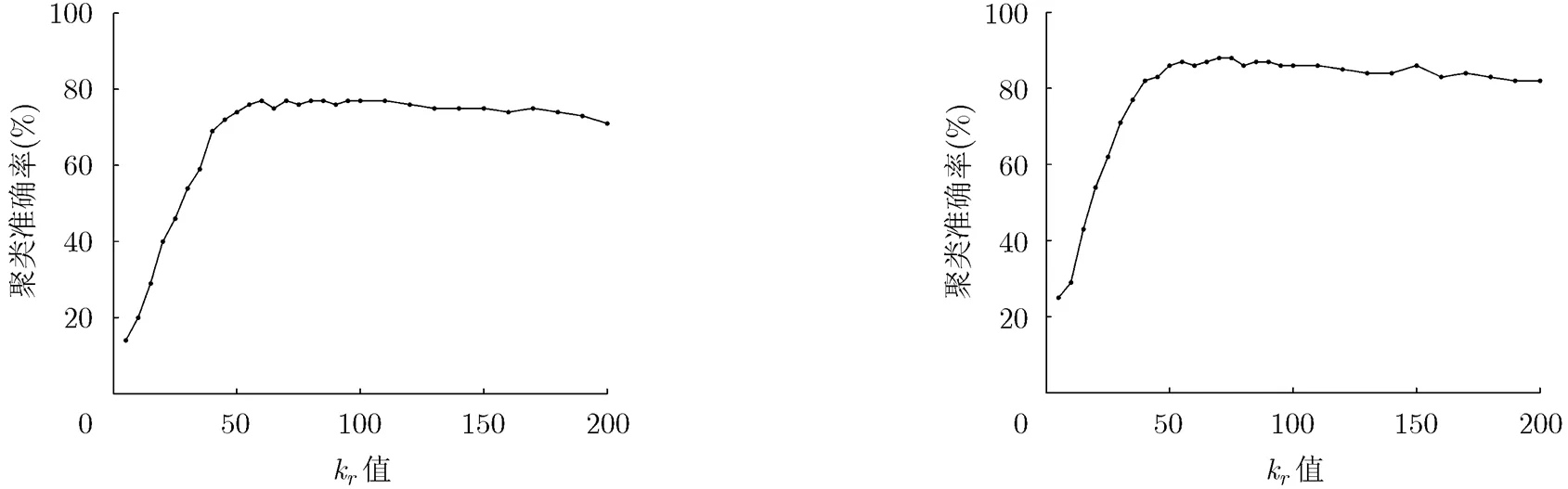
图1 kr对papers的影响 图2 kr对authors的影响
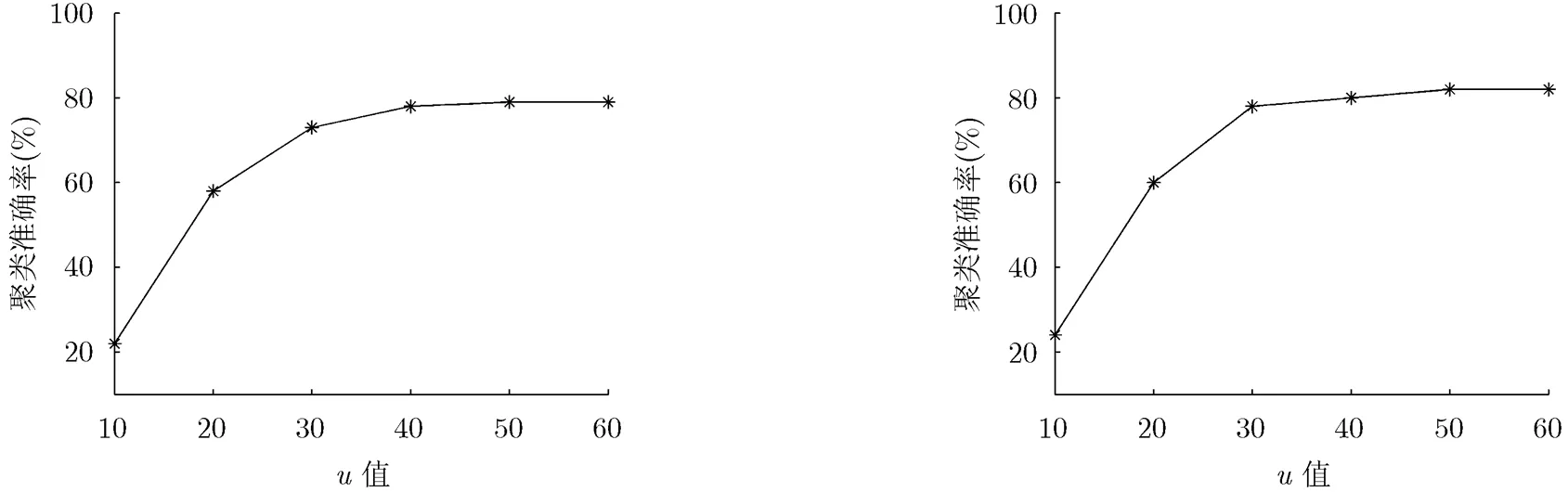
图3 u对papers的影响 图4 u对authors的影响
4.4聚类稳定性对比
本文选择复杂度较低的通用算法CIT[6],基于排序的算法NetClus[8]与本文算法FCAET做稳定性比较。算法ComClus是NetClus的衍生算法,性质类似,这里不做分析。本次实验在小数据集S1上聚类目标数据集papers,以比较3个算法CIT,NetClus及FCAET的稳定性。3个算法的10次实验准确率如图5所示,虽然算法FCAET和算法NetClus的计算速度都很快,但图5的实验数据说明本文算法FCAET的稳定性更好,初始中心点的选择对聚类结果影响不大,而算法NetClus不是很稳定,初始类的划分对算法NetClus的函数及收敛速度影响非常大。当异构信息网络稀疏时,算法CIT的收敛速度比较慢,当迭代次数很小时,聚类精度并不高。

图5 3个算法10次实验聚类准确率比较
4.5聚类准确率及计算速度的对比
基于半正定的规划算法[5]以及谱聚类算法[7]时间复杂度过高,不适合聚类规模较大的异构信息网络。本文选择复杂度较低的通用算法CIT[6],基于排序的算法NetClus[8],及NetClus的衍生算法ComClus[11]与本文算法FCAET做准确率及计算速度的比较。算法NetClus, ComClus的参数均取文献[8]给定的实验参数。每个算法都涉及到初始划分,初始划分影响聚类结果,因此,对于每个目标数据集,所有算法均做3次实验,3次实验中聚类准确率最高的一次作为该算法的准确率,本次实验的计算速度作为该算法的计算速度。聚类准确率对比结果如表3所示,表3数据说明本文算法的聚类准确率高于其他算法。算法CIT计算复杂度(2),当异构信息网络稀疏时,算法CIT的收敛速度比较慢,故聚类精度并不高。算法NetClus只使用了异构数据关系,故聚类精度较低。算法ComClus利用了同构数据的关系,聚类精度高于NetClus的聚类精度,但也增加了计算复杂度。本文算法是一种基于图嵌入技术的聚类算法,而且采用通勤距离度量能够更加充分表现数据之间的关系,并且收敛性速度不受关系矩阵的稀疏性影响,同时也能够利用目标数据集的同构关系,故聚类精度高。计算速度对比结果如表4所示,表4数据说明本文算法的计算时间基本等同于算法NetClus的计算时间。但本文算法FCAET通用性更强,可以用于任何一个星型网络模式的异构信息网络的聚类。而算法NetClus及ComClus需要根据具体应用领域设计函数,依赖于数据特性,不具有普遍性。
4.6FCAET运行时间分析
算法FCAET在两个数据集上的运行时间分布情况如表5所示,实验说明本文算法的运行效率是很高的。3个指示子集的串行计算速度占程序运行时间50%左右。若并行计算3个指示子集,速度会更快。求解模型极小值也可采用并行执行以提高计算速度。
表3聚类准确率比较(%)

目标对象CITNetClusComClusFCAET S1的papers73.9171.5472.8378.87 S1的authors74.4169.1374.9181.33 S2的papers70.8471.2872.9376.36 S2的authors71.0268.2973.0177.94
表4计算速度比较(s)

目标对象CITNetClusComClusFCAET S1的papers 78.5 37.3 40.3 37.1 S1的authors 79.8 36.9 39.8 38.3 S2的papers1459.3792.6817.3798.4 S2的authors1474.7733.7771.4764.9
表5算法FCAET运行时间分配情况(s)

目标对象嵌入计算时间聚类时间时间总和 S1的papers 19.6 17.5 37.1 S1的authors 18.1 20.2 38.3 S2的papers393.8405.6798.4 S2的authors376.4388.5764.9
5 结束语
本文提出的异构信息网络快速聚类算法不同于以往的异构数据聚类算法,本文算法根据每个关系矩阵先求解指示目标数据集的每个指示数据集,然后根据指示数据之间的关系建立模型,从而得到目标数据集的划分。本文算法通用性强、稳定性好,同时计算速度快而且聚类准确率高,非常适合异构信息网络的聚类。而以往的聚类算法要么时间复杂度过高,要么通用性不强,聚类结果不稳定。通过理论分析及实验验证,本文算法的计算速度和聚类准确率满足要求。本文算法中各关系矩阵的权重影响着目标数据集的划分,这些权重还不能自适应确定,需要进一步研究。当异构数据关系不再稀疏,网络模式不再是星型的,如何快速划分任意模式的大规模异构信息网络,都是亟待解决的问题。
[1] 肖杰斌, 张绍武. 基于随机游走和增量相关节点的动态网络社团挖掘算法[J]. 电子与信息学报. 2013, 35(4): 977-981.
Xiao Jie-bin and Zhang Shao-wu. An algorithm of integrating random walk and increment correlative vertexes for mining community of dynamic networks[J].&, 2013, 35(4): 977-981.
[2] 陈季梦, 陈家俊, 刘杰, 等. 基于结构相似度的大规模社交网络聚类算法[J]. 电子与信息学报. 2015, 37(2): 449-454.
Chen Ji-meng, Chen Jia-jun, Liu Jie,.. Clustering algorithms for large-scale social networks based on structural similarity[J].&, 2015, 37(2): 449-454.
[3] Sun Y and Han J. Mining heterogeneous information networks: principles and methodologies[J].:,2012, 3(2): 1-159.
[4] Huang Y and Gao X. Clustering on heterogeneous networks [J].:, 2014, 4(3): 213-233.
[5] Gao B, Liu T Y, Zheng X,.. Consistent bipartite graph co-partitioning for star-structured high-order heterogeneous data co-clustering[C]. Proceedings of the 11th ACM SIGKDD International Conference on Knowledge Discovery in Data Mining, Chicago, 2005: 41-50.
[6] Gao B, Liu T, and Ma W-Y. Star-structured high-order heterogeneous data co-clustering based on consistent information theory[C]. Proceedings of the 6th International Conference on Data Mining (ICDM 2006), Hong Kong, 2006: 880-884.
[7] Long B, Zhang Z M, Wu X,.. Spectral clustering for multi-type relational data[C]. Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, 2006: 585-592.
[8] Sun Y, Yu Y, and Han J. Ranking-based clustering of heterogeneous information networks with star network schema[C]. Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, 2009: 797-806.
[9] Li P, Wen J, and Li X. SNTClus: a novel service clustering algorithm based on network analysis and service tags[J]., 2013, 89(1): 208-210.
[10] Li P, Chen L, Li X,.. RNRank: Network-Based Ranking on Relational Tuples[M]. Boston: Behavior and Social Computing, Springer International Publishing, 2013: 139-150.
[11] Wang R, Shi C, Philip S Y,.. Integrating Clustering and Ranking on Hybrid Heterogeneous Information Network[M]. Berlin: Advances in Knowledge Discovery and Data Mining, Springer Berlin Heidelberg, 2013: 583-594.
[12] Boden B, Ester M, and Seidl T. Density-Based Subspace Clustering in Heterogeneous Networks[M]. Berlin: Machine Learning and Knowledge Discovery in Databases, Springer Berlin Heidelberg, 2014: 149-164.
[13] Meng Q, Tafavogh S, and Kennedy P J. Community detection on heterogeneous networks by multiple semantic- path clustering[C]. 2014 6th IEEE International Conference on Computational Aspects of Social Networks (CASoN), Porto, 2014: 7-12.
[14] Meng X, Shi C, Li Y,.. Relevance Measure in Large-scale Heterogeneous Networks[M]. Boston: Web Technologies and Applications, Springer International Publishing, 2014: 636-643.
[15] Aggarwal C C, Xie Y, and Philip S Y. On dynamic link inference in heterogeneous networks[C]. SIAM International Conference on Data Mining, Anaheim, 2012: 415-426.
[16] Khoa N L D and Chawla S. Large Scale Spectral Clustering Using Resistance Distance and Spielman-teng Solvers[M]. Berlin:Discovery Science, Springer Berlin Heidelberg, 2012: 7-21.
[17] Spielman D A and Teng S H. Nearly-linear time algorithms for graph partitioning, graph sparsification, and solving linear systems[C]. Proceedings of the 36th Annual ACM Symposium on Theory of Computing, Chicago, 2004: 81-90.
[18] Spielman D A and Teng S H. Nearly linear time algorithms for preconditioning and solving symmetric, diagonally dominant linear systems[J]., 2014, 35(3): 835-885.
[19] Fouss F, Pirotte A, Renders J M,.. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation[J]., 2007, 19(3): 355-369.
[20] Spielman D A and Srivastava N. Graph sparsification by effective resistances[J]., 2011, 40(6): 1913-1926.
[21] Achlioptas D. Database-friendly random projections[C]. Proceedings of the 20th ACM Sigmod-Sigact-Sigart Symposium on Principles of Database Systems, New York, 2001: 274-281.
[22] Koutis I, Miller G L, and Tolliver D. Combinatorial preconditioners and multilevel solvers for problems in computer vision and image processing[J]., 2011, 115(12): 1638-1646.
A Fast Clustering Algorithm Based on Embedding Technology for Heterogeneous Information Networks
Chen Li-min①②Yang Jing①Zhang Jian-pei①
①(,,150001,)②(,,157012,)
Research on clustering heterogeneous information networks is one of the current hotspots. Taking advantages of the sparsity of heterogeneous information networks, a fast clustering algorithm based on embedding technology for heterogeneous information networks of star network schema is proposed in this paper. First, the heterogeneous information network is transformed into some compatible bipartite graphs from the point of compatible view. Then, the approximate commute distance embedding of each bipartite graph is computed via random mapping and a linear time solver, and an indicator subset in each embedding indicates the target dataset. At last, a general model is formulated via all the indicator subsets, and a minimum value of the model is derived by simultaneously clustering all of the indicator subsets using the sum of the weighted distances for all indicators for an identical target object. This proposed algorithm is effective by theory analysis and experimental verification.
Heterogeneous information network; Clustering; Commute distance; Embedding; Sum of weighted distances
TP311
A
1009-5896(2015)11-2634-08
10.11999/JEIT150106
2015-01-21;改回日期:2015-07-16;
2015-08-25
陈丽敏 chenlimin_clm@126.com
国家自然科学基金(61370083, 61073043, 61073041);高等学校博士学科点专项科研基金(20112304110011, 20122304110012)
The National Natural Science Foundation of China (61370083, 61073043, 61073041); The National Research Foundation for the Doctoral Program of Higher Education of China (20112304110011, 20122304110012)
陈丽敏: 女,1970年生,副教授,博士生,研究方向为数据挖掘、机器学习.
杨 静: 女,1962年生,教授,博士生导师,研究方向为数据库与知识库.
张健沛: 男,1956年生,教授,博士生导师,研究方向为数据库与知识库.

