例谈高中数学必修课程选修化

●浙江省杭州高级中学钱江校区 俞 昕

例谈高中数学必修课程选修化

●浙江省杭州高级中学钱江校区 俞 昕

如今选修课正如火如荼地开展着，在风光华丽的外表下面，实际的情况还着实有些令人担忧.作为一线教师，笔者觉得我们应该面对现实，在实践中不断反思、勇于直面问题，并且敢于尝试解决问题，让我们的数学选修课程在整个选修课程开发过程中留下精彩的一笔.

一、数学选修课程实施现状

浙江省新课改之后，有一种声音：数学的地位只升不降，因为取消了文理分科，在高考中数学显得越发重要.这样的现状使得数学选修课程处于非常尴尬的境界.

1.学生对数学选修课程的认识不到位

在学生心目中，从小学到高中数学一直是主科，学习数学的主要目的可能大都是为了考试，利用数学这门能够体现区分度的学科让自己在考试中取得优势地位，从而在竞争中脱颖而出.因此，即使开设数学选修课程，但在学生心目中仍然难以改变数学必修课程的位置.很多学生有一种认识误区：数学选修课程其实就是数学必修课程的一种“伪装”，或是扶差，或是培优.在笔者所在学校就出现了意想不到的现象：很多学生整个下午四节课全部选报了数学选修课程，他们认为自己的数学比较薄弱，想通过多听听数学课提高自己的数学成绩.而大部分学生至少选报了一门数学选修课程，因为他们认为多上上数学课，多多少少对自己的数学成绩会有所帮助.显然，学生对数学选修课程的认识是不到位的.

2.教师对数学选修课程的观念认识不深刻

笔者所在学校要求每一位数学教师都要开设选修课程，由于平时的必修课教学任务已经比较繁重，所以很多数学教师将数学选修课程演变成数学习题课，选修课的备课就成为准备几道数学题目，这倒也恰好与学生对数学选修课程的态度不谋而合，师生都将数学选修课程看成是数学扶差课或培优课了.其实这也反映出教师不善于开发选修课程，对数学选修课程的认识不深刻、不到位.

3.学校对数学选修课程的把握不明确

选修课程的开设势必对必修课程造成一定的冲击，数学必修课程课时减少，原本的进度加快，原本的教学内容要压缩，确实造成了数学教学课时的紧张.因此，校方与教师都认为将数学选修课程演变成数学扶差课或培优课是无可厚非的，校方一般也就默认了一线教师的这种处理方法.

但以上现象是否表明学生真的喜欢数学选修课，数学选修课是否真正发挥了它应有的价值与功能呢？这是值得我们数学教师反思的.数学选修课与必修课之间的矛盾如何解决？笔者结合自身的选修课程教学实践，从“必修课程选修化”的角度来探讨数学选修课程教学.

二、数学必修课程选修化

数学选修课程的开设应该试图让学生认识数学的本质，改变对传统“考试数学”的认识，体验数学中蕴含的丰富的思想方法，变“被动学数学”为“主动学数学”，通过提升探究数学的兴趣从而提高数学成绩，而不是靠单纯的题海战术提高成绩，因为靠题海战术是“治标不治本”的做法.如何兼顾数学选修课程与必修课程呢？笔者认为必修课程的选修化是可行之策.

1.对必修课程中数学公式来龙去脉的深入开发

高中数学中有很多新的公式，在必修课程的教学中，教师最多就是把公式推导出来，然后就着重进行公式应用的探究了，这也是常态课的一般表现.由于必修课课时的限制，教师可能无法向学生充分展示数学公式的来龙去脉，深入挖掘数学公式，开发蕴含于数学公式中的丰富资源.而数学选修课就可以为我们提供这样的机会，进行必修课程的二次开发，将必修课程选修化.下面以“两角差的余弦公式”为例进行探讨，教师可以从多角度、全方位向学生展现公式的全貌.（人教A版教材中用向量数量积推导在此省略）

视角1：两锐角差的余弦公式.

（1）你能用这两块三角板（如图1）拼出哪些角度呢？（2）你能用它们拼出15°的角吗？（3）你能否利用所拼出的图形（如图2或图3）求出cos15°的值吗？

（4）若将上面的45°和30°角分别改成锐角α和β，那么会有怎样的结论？cos（α-β）=？

图1

图2

图3

视角2：两锐角差的余弦公式.

如图4所示，为一个坡度为30°的斜坡.已知作用在物体上的力F与水平方向之间的夹角为45°，且大小为10N，在力F的作用下，物体沿斜坡运动了2m，求力F作用在物体上的功W.

图4

图5

由此做功问题提炼出图5所示的“两锐角差的余弦公式”的模型，若将特殊角替换成一般角便可以得到两锐角差的余弦公式cos（α-β）=cosαcosβ+sinαsinβ.让学生从实际问题情境中提炼出两锐角差的余弦公式的模型，感知数学知识来源于实际，运用于实际，自然界万事万物中都蕴含着丰富的数学变换.

视角3：两锐角差的余弦公式.

公元3世纪末，亚历山大数学家帕普斯在《数学汇编》中给出命题：如图6，设H是以AB为直径的半圆上的一点，CE是半圆在点H处的切线，CH=HE.CD和EF为AB的垂线，D、F是垂足，则（CD+EF）·CE=AB·DF.认识“弦图”，从平面几何中发现两锐角差的余弦公式.

图6

图7

（1）如图7所示，设∠HOF=α，∠COH=β，试用α、β表示∠EOF；

（2）不妨设OC=OE=1，试用线段（比）分别表示sinα、cosα、sinβ、cosβ及cos（α-β）；

（3）试探究cos（α-β）与sinα、cosα、sinβ、cosβ的关系.

让学生寻求数学进步的历史轨迹，领会数学的美学价值，提高学生的数学文化素养.

此外，古埃及天文学家托勒密利用两角和、差的三角关系绘制了现存最早的三角函数弦表，在天文学和测量计算中有很重要的应用.制作弦表的原理如图8所示.此原理与人教A版上的方法（如图9所示）有异曲同工之妙.

图8

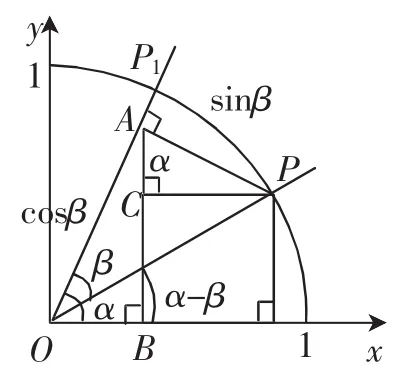
图9

视角4：两锐角差的余弦公式.

数学的魅力在于它能让人惊叹于数学的各种奇妙的变换，一个普通的图形当中竟然也能蕴藏着“两锐角差的余弦公式”，如图10所示.通过简单的三角形等积就可以非常简单地得到“两锐角差的余弦公式”.

图10

视角5：两任意角差的余弦公式.人教A版选修4-2《矩阵与变换》中有介绍旋转变换.如图11所示，在直角坐标系xOy内，作单位圆O，设α、β角的始边都为Ox，终边分别交圆于A、B.这时，得到两点间的坐标分别为A（cosα，sinα）、B（cosβ，sinβ）.由两点间的距离公式，并整理得AB2=2-2（cosαcosβ+sinαsinβ） ①.再以OB为横轴，建立新的直角坐标系x′O′y′，使其单位长度与原坐标系相同.在新坐标系中两点坐标为A（cos（α-β），sin（α-β））、B（1，0）.同样，由两点间的距离公式，并整理得AB2=2-2cos（α-β） ②.由①②便可得两任意角差的余弦公式.

图11

人教社全日制普通高中教材中也是运用类似的变换来推导“两任意角差的余弦公式”的,只不过不是旋转坐标轴，而是旋转点（在此不累述，详见人教社全日制普通高中教材）.

2.对必修课程中数学知识关联性的深入开发

在日常的必修课教学中，教师往往会忽略数学知识之间的关联性，也容易给学生造成一些误区.于是我们可以利用必修课程选修化让学生认识到数学的关联性.

比如在正弦定理与余弦定理的教学中，很多学生包括一些教师都会出现这样的误区：对于（1）已知三角形两边及其中一边的对角，（2）已知三角形两角及一边，我们能运用正弦定理解三角形，但对于（3）已知三角形两边及夹角，（4）已知三角形三边，运用正弦定理就无法解决了，只能通过余弦定理解三角形.出现以上误区的原因就在于师生对于正弦定理与余弦定理的关联性缺乏应有的认识.针对以上问题，我们可以对此进行必修课程选修化的开发，对学生深刻认识正弦定理与余弦定理必有裨益.下面笔者撷取其中一角以窥一斑.

正弦定理和余弦定理是刻画三角形6个基本元素中4个元素之间的基本关系.解三角形除了应用这两个定理，还有一个定理，即射影定理：a=bcosC+ccosB（另两个略）.更进一步讲：正弦定理、余弦定理、射影定理三者之间是等价的.

比如由正弦定理可以推出余弦定理.

由三角形内角和定理知cosA=-cos（B+C）=sinBsinC-cosBcosC，两边平方得cos2Bcos2C=sin2Bsin2C+cos2A-2sinBsinCcosA.

即 （1-sin2B）（1-sin2C）=sin2Bsin2C+（1-sin2A）-2sinBsinCcosA.

化简得sin2A=sin2B+sin2C-2sinBsinCcosA （2）.

将（1）式代入（2）式，并化简得a2=b2+c2-2bccosA.

由余弦定理也可以推出正弦定理.

a2=b2+c2-2bccosA （1），b2=a2+c2-2accosB （2）.

（1）-（2）得a2-b2=b2-a2-2bccosA+2accosB.

则2（a2-b2）=2c（acosB-bcosA）.

正余弦定理与射影定理的等价性亦可证明，在此省略.由此可以看出，正弦定理与余弦定理的等价性，不存在问题只能用正弦定理或余弦定理解决，我们只能说哪些问题运用正弦定理或余弦定理能一步到位解决.

此外，数学的关联性还体现在数学思维的相似性上，还是以余弦定理为例，图12揭示了不同数学知识之间的关联性与相似性.

图12

3.对必修课程中开放性元素的深入开发

开放性教学旨在思维开放、题目开放、过程开放.由于对开放性问题的评分存在种种困难，因此，在高考中鲜有开放性问题出现.由此引起的连锁反应是：数学教师在日常的教学中也鲜有涉及开放性问题.必修课程选修化可以对必修课程中的开放性元素进行深入开发，进一步开发学生潜藏的数学能量.比如下面关于数列知识的一个开放性教学案例.

（1）题由根生.

摘自高中数学人教A版必修5第48页：一尺之棰，日取其半，万事不竭.（《庄子·天下篇》）

变式：今年，某浙人语：一数为十，日减其一，竭否？（从古至今）

摘自高中数学人教A版必修5第28页：传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数.他们研究过如图13所示的三角形数.

图13

从以上的例子中，我们共得到3个数列，请分别写出这三个数列.

（2）固本培元.

对以上这3个数列，我们可以进行怎样的研究？

（3）开枝散叶.

对于单个数列，可进行各种变换（取绝对值、取倒数、取子列等），得到新的数列，请选取某几个角度进行研究.

（4）节外生枝.

对于两个数列，可进行各种运算（加、减、乘、除等），得到新的组合数列，请选取某几个角度进行研究.

下面的案例是基于一道高考题的题干部分进行的开放性教学活动.

编题活动1：2014年重庆高考题题干“条件1”：已知直线l：ax+y-2=0.请你根据以上题干“条件1”，运用“直线方程”知识点编拟一些问题，可适当添加一些条件.

编题活动2：2014年重庆高考题题干“条件2”：圆心为C的圆（x-1）2+（y-a）2=4.请你根据以上题干“条件2”，运用“圆的方程”知识点编拟一些问题，可适当添加一些条件.并指明你编拟的题目考查了哪些知识点.

编题活动3：2014年重庆高考题题干“条件1”：已知直线l：ax+y-2=0与“条件2”：圆心为C的圆（x-1）2+（y-a）2=4.请你综合以上题干“条件1”和“条件2”，运用直线和圆的方程的知识点编拟一些问题，可适当添加一些条件.

以上两个开放性教学案例事实上是开放条件或结论的编题活动.基于选修课的拓展性，我们的开放度还能更大一些，渗透数学研究性学习与数学建模的元素.比如可以设计一个开放性的数学活动：设计制作一个1升的可乐包装罐，形状不定，但要节省材料.各种形状的设想确定了用料最省时的尺寸（必须通过函数最值的计算确定），而最终要选出最满意的设计，还要比较所有的方案才能得到.这种开放性的活动给学生提供了更广阔的开放性思维的机会，是培养开放性思维能力的好途径.再比如高中数学中的经典内容“杨辉三角”，可以把杨辉三角的数学内涵无限开放，如从“杨辉三角”到“帕斯卡三角”看中西方数学发展；用“组合数学”研究“杨辉三角”的数学规律；从数列的视角研究“杨辉三角”等.

三、结束语

必修课程选修化不仅是数学选修课程开发的一个广阔途径，而且有利于提高学生的数学学习兴趣、端正学生对数学选修课的态度、纠正教师队伍中对数学选修课认识上的一些误区、衔接数学必修课程、提升学生的数学能力与素养.从另一角度来看，深入数学必修课程，对其内涵、广度、深度不断挖掘，也是培养教师选修课程开发能力的一个有力途径.A