研究性学习在初中数学中的应用

朱明光

[摘   要] 研究性学习是一种新型学习模式，在数学领域中，研究性学习是一种有效的学习方法，能让学生主动参与到学习中，主动动手、动脑。初中数学的研究性学习必须尊重学生自身理念，侧重培养学生独立问题意识以及思考能力，培养他们的创新思维，促进学生理解力的提高和个人的全面发展。研究性学习的开展要从基础教育入手，从学习活动中培养学生的思维能力。

[关键词] 初中;研究性学习活动;问题分析

研究性学习是一种新型学习模式，这种模式和接受式学习模式有较大差别。但从实际应用情况来看，研究性学习和接受式学习模式既要对立，又要互相补充、高度结合。尤其是在数学领域中，研究性学习是一种有效的学习方法，让学生主动参与到学习中，主动动手、动脑。但是从应用现状来看，研究性学习还存在许多问题，还需要不断完善和补充。因此，探究在初中数学教学中开展研究性学习活动具有实用价值。

一、研究性学习实施的方式

1.数学开放题

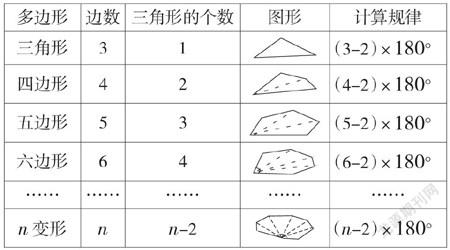
开放题答案并不唯一，主要特征是题目的不完整性、解题思维的多元化和解答方式的发散性，比如在教授学生学习多边形的内角与定理时，就要设置相应的探究课题，如下图所示，显示了多边形主要的类型及边数、图形等，学生就要自行完成表格，挖掘规律。通过研究，学生就能得出结论：n边形的内角与定位为（n-2）×180°。

从上面这个例子可知，解答开放性习题非常自由，学生一定要全身心投入到学习中去，如果仅仅依靠自身的基础知识，死记硬背是不可能解决相应问题的。研究中要从多个角度思考问题，在思考过程中获得原创性结果。

2.变式练习

初中数学研究性学习的变式练习主要有两种模式，即过程性变式练习和概念性变式练习。概念性变式练习是通过概念或非概念变式解释本质属性或非本质属性的练习方式，学生通过多角度理解数学概念，构建和传统相联系的新型概念;过程性变式练习为利用变式方式体现存在的知识及发展过程的练习方式，运用此方式学生能了解知识形成的全过程，进而了解问题的本质。

3.竞赛与建模

在研究性活动中知识竞赛也是一种重要的学习方式，初中数学竞赛以解决问题为核心，让中学生在自由竞争环境中逐渐累积自身的数学知识，锻炼逻辑思维能力。

数学建模就是针对某一种特定事物，应用数学类语言描述一种特有的数学结构。把复杂问题抽象化、简明化，通过实践检验结果准确性，在实施过程中学生需要通过个人能力建模。所以建模前必须经过一段时间的专业学习，培养灵活的思维能力，这种研究性学习活动能快速提高学生的思维能力。

二、研究性学习活动中存在的问题

1.实施过程中的问题

从实施现状来看，许多教师还没意识到初中数学教学中的研究性学习存在的问题。

（1）研究性学习和接受性学习并非对立，而是互相补充的。从教育实践来看主要存在两种不同类型的教育模式：一种是系统传授形式，学习者从中接受人类已有知识;其二是学生从学习中学会探索及研究，体验到使用知识的乐趣，自己构建知识体系。假如将以前的教育称之为传授性的教育，对应的学习方式为接受性学习，那么相对的教育即为体验性教育，与之相适应的学习方式是研究性学习。

研究性学习是针对接受性学习所提出的，这两种方式在一定程度上能互补。事实上，研究性学习和传授性学习各有所长：研究性学习重在积累学生的直接经验，培养学生创新精神及思维，促进学生的理解能力等各个方面的发展;接受性学习重在积累学生的间接经验，传递系统学科知识。因此如果仅仅从人的全面发展的角度来看，两种学习方式都比较重要，缺一不可。换言之，假如对基本知识技能模仿掌握不到位，非模仿性的思维也就是无本之木、无源之水。传统教学观念比较重视知识传授，强调死记硬背、接受学习及机械训练，压抑学生学习的主动性，影响学生创新精神及实践能力的培养。研究性学习不过是让研究回到课程中应有位置，并非看轻接受学习的价值。这两种方式在初中学习中都是必要的。

（2）学习活动要具有灵活性。研究性学习和其他的学习方式是互补的，针对初中基础教育情况，学生应该以系统知识及技能为主。初中数学具有抽象性的特征，因此实施研究性学习就要具备一定灵活性。教师要依据不同内容，选择不同途径，以某一个问题作为中心组织教学，在课堂上实施研究性学习;当然也可以让学生在课外采取研究性学习方式进行观察、调查、考察;亦可采取理论和实践相结合的方式开展。

2.研究性学习活动的认识问题

许多初中数学教师认为研究性学习不过是数学活动或者数学实验，根本没有认识到应该采用哪种学习方式，应该认识哪些问题。本文就从研究性学习的几种方式进行分析。

（1）数学开放题。开放题的答案并不唯一，在设问上也要求学生从多角度、多方面及多层次进行探索，这种题的特征为：其一，非完备性，也就是题目不完整;其二，不确定性，没有确定条件、结论或者解题策略。从解答过程与策略来看，具有发散性、层次性、探究性及创新性几个特征。

在解答开放题过程中，因为缺乏固定的现成模式，学生仅仅靠机械模仿、死记硬背是无法解答问题的，所以在学习中学生就要调动自己所储备的知识，积极进行探索活动，多种思维、多角度地实施探索，在这个思维过程中必定存在模仿性。

（2）数学变式练习。所谓变式就是确保事物的本质属性不变，变换其非本质属性，突出其本质属性的思维方式。变式不但能发展学生认知，还能通过转换、演绎、运动、变化等方式渗透数学思想，不但有利于开阔学生眼界，活跃学生思维，还有利于学生理解数学知识的多维性与变通性，让知识融会贯通。

（3）数学竞赛与建模。初中数学竞赛能够展示出数学思想，普及数学文化，对培养创新数学能力具有独特功能，不但能培养学生创新思维，还能培养学生的发散思维能力。但是初中数学竞赛问题并非是将数学内容简单地叠加，而是要对学生所掌握知识从多个角度和方面实施非本质变异，从而形成新问题，这种问题和设立问题的情景与学生认知结构间存在一定距离，学生只有具备了极强变通性才能随着问题变化而变化。

数学建模属于狭义角度的建模，就是将不规范的、复杂的问题进行抽象简化为明确变量与参数之数学关系，即为建立数学模型。还要使用数学方法对问题进行解析或者求解，将结果纳入到实际中进行验证及解释。主要有三个步骤：其一，实际问题数学模式;其二，数学模式数学的解;其三，数学的解实际问题的解。对于一个抽象模型而言，并非只有一个正确的模型，很多模型都能解决相同问题。同时一个抽象模型还能够解决多个具体问题，并没有一个固定方法和规定的数学工具，也无现成答案及模式能够遵循。需要学生运用所学知识综合分析问题，跳出习惯的解题套路、思维模式，采取一种较为灵活、具有创造性的学习方法。

初中数学中开展的研究性学习和大学研究活动存在极大差异，就是要从基础教育入手，从学习活动中培养学生思维能力。初中数学的研究性学习必须尊重学生自身理念，侧重培养学生独立问题意识以及思考能力，培养他们的创新思维，促进学生理解力的提升和个人的全面发展。

参考文献

[1]谢术彦.初中数学开展研究性学习的体会[J].2010，（07）.

[2]庄桂辉.浅论中学数学的研究性教学[J].科技咨询导报，2010，（56）.

[3]陈元.浅析初中数学中的研究性学习[J].考试周刊，2014，（33）.

[4]龙开奋.奥赛题与探究性课题相结合的初步构想[J].数学教育学报，2012，（04）.

责任编辑 王 慧