2015 年高考导数压轴题解题探究
孙丽娟
(云南省会泽县茚旺高级中学)
【考点介绍】
1.导数与函数单调性、极值、最值的直接应用.
2.交点与根的分布.
3.不等式证明:(1)作差证明不等式;(2)变形构造函数证明不等式;(3)替换构造不等式证明不等式.
4.不等式恒成立求字母范围(“两分法”):(1)恒成立之最值的直接应用;(2)恒成立之分离参数;(3)恒成立之讨论字母范围.
5.导数与函数性质的综合运用.
6.导数与三角函数结合.
【常用结论记忆】
(三)不等式的证明(作差法、变形构造函数法、替换构造函数法)
(最值、作差、变形构造函数、替换构造函数)已知函数f(x)=ln(x+1)-x.
(1)求函数f(x)的单调递减区间.
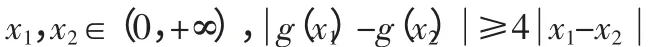
2.ex>x+1,x>0.
3.x>ln(x+1),x>0.
4.ln x<x<ex,x>0.
【例题讲解】
(一)导数与函数单调性、极值、最值的直接应用
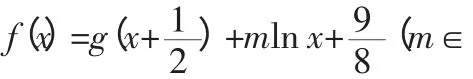
(四)不等式恒成立求字母范围
(1)若曲线y=f(x)在点P(2,f(2))处切线方程为y=3x+1,求函数f(x)的解析式.
(2)讨论函数f(x)的单调性.
(1)求g(x)的表达式.
(2)当m=e 时,求曲线f(x)在点(e,f(x))处的切线方程及函数f(x)的单调区间.
(3)若埚x∈R+,使f(x)<0 成立,求实数m 的取值范围.
(4)若x∈(0,+∞),f(x)≤0 恒成立,求实数m 的取值范围.
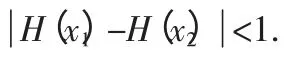
(1)当a=0 时,求曲线y=f(x)在(0,f(0))处的切线方程.
(2)当x≥1 时,若关于x 的不等式f(x)≥0 恒成立,求实数a的取值范围.
(3)当x≥0 时,若关于x 的不等式f(x)≥0 恒成立,求实数a的取值范围.
3.(分离常数)已知函数
(1)试判断函数f(x)在(0,+∞)上的单调性并证明你的结论.
(6)若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数m 的取值范围.
(二)交点与根的分布
(交点个数与根的分布)已知x=3 是函数f(x)=aln(1+x)+x2-10x 的一个极值点.
(1)求a.
(2)求函数f(x)的单调区间.
(3)若直线y=b 与函数y=f(x)的图象有3 个交点,求b 的取值范围.
(3)求证:(1+1×2)(1+2×3)…[1+n(n+1)]>e2n-3.
(1)求函数f(x)的单调区间.
(1)求a,b 的值.
(五)导数与函数的综合应用
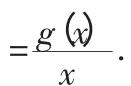
(1)求a,b 的值.
(2)不等式f(2x)-k·2x≥0 在x∈[-1,1]上恒成立,求实数k的范围.
(六)导数与三角函数结合
已知函数f(x)=x,函数g(x)=λf(x)+sin x 是区间[-1,1]上的减函数.
(1)求λ 的最大值.
(2)若g(x)<t2+λt+1 在x∈[-1,1]上恒成立,求t 的取值范围.

