二次函数的“隐形”应用
2015-07-12 07:23胡上生
新课程(中学) 2015年10期
胡上生
(江西省信丰中学)
二次函数是高中最重要的基本初等函数之一,是各章节知识之间连接的纽带与载体.有这样一类函数,表面上看起来不是二次函数,但实际上换元之后得到一个二次函数,由此可以利用二次函数的性质来解决这类问题,像这类函数称之为“隐形”的二次函数.下面笔者通过具体实例来认识二次函数的“隐形”应用.

简解:令3x=t,则t>0,从而问题就等价转化为一元二次方程t2+(4+a)t+4=0 在(0,+∞)上有两个实根.再令f(t)=t2+(4+a)t+4(t>0),

简解:原方程等价于m=-cos2x+2cosx,由于cos2x=2cos2x-1,
所以m=-2cos2x+cosx+1,m 是关于cosx 的二次函数,这就是
例5.设函数f(x)=ax2-2x+2,对于满足1<x<4 的一切x 值,都有f(x)>0,求实数a 的值.
简解:由于原二次函数的开口方向及对称轴都未知,所以利用
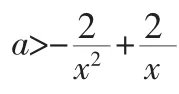
通过上述几例,不难发现“隐形”的二次函数其实就是外层函数为二次函数,内层函数为各类函数的复合函数,它在高中数学解题中有着广泛的应用,并且运用过程中又贯穿着函数与方程,转化与归化,分类与整合等重要的数学思想方法.
猜你喜欢
中学生数理化·七年级数学人教版(2021年12期)2021-12-31
艺术大观(2020年11期)2020-10-09
数理化解题研究(2020年8期)2020-03-30
——信丰阁
城乡建设(2019年14期)2019-02-20
现代园艺(2018年1期)2018-03-15
中学教学参考·理科版(2017年8期)2018-02-24
新高考·高二数学(2017年3期)2017-08-17
中学生数理化·高三版(2017年2期)2017-04-21
福建中学数学(2017年1期)2017-04-21
中学教研(数学)(2015年3期)2015-12-08

