导数与不等式联姻的解决策略
孙建山
(江苏省六合高级中学)
例1.(2008 江苏高考数学第14 题)f(x)=ax3-3x+1 对于x∈[-1,1]总有f(x)≥0 成立,则a=______.
解法1(分离参数):由题意可得:ax3≥3x-1 在x∈[-1,1]上恒成立.
(1)当x=0 时,不等式显然恒成立,此时a∈R.
综上:a=4.
此解法通过分离参数转化成a≥h(x)或者a≤h(x),然后求h(x)的最值,当然有些题目也可以转化成ag(x)≥h(x)或者ag(x)≤h(x)[也就是说不需要把与a(也可能是关于a 的参数团)相乘的关于a 的代数式都除到另一边],当然ag(x),h(x)最好是我们比较熟悉的一些函数,然后通过图像等方法求出a 的数值或者范围.
此解法并未上来就求导讨论导函数的符号,而是通过取特值先适当缩小参数a 的范围,然后再求导,这样在许多的情况下可以适当简化讨论.
例2.(2015 山东高考数学理第21 题)设函数f(x)=ln(x+1)+a(x2-x),其中a∈R.
(1)讨论函数f(x)极值点的个数,并说明理由;
(2)若坌x>0,f(x)≥0 成立,求a 的取值范围.
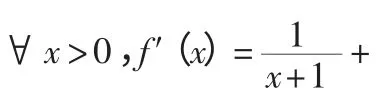
此解法借助导函数的符号确定参数的取值范围,然后对参数取值范围以外的部分进行分析验证其不符合题意,即可确定所求参数的范围.解法1 和解法2 同样适用此题.
下面笔者选两题可供读者练习:
1.(2010 新课标第21 题)设函数f(x)=ex-1-x-ax2.
(1)若a=0,求f(x)的单调区间;
(2)若当x≥0 时f(x)≥0,求a 的取值范围.
2.(2012 天津理第20 题)已知函数f(x)=x-ln(x+a)的最小值为0,其中a>0.
(1)求a 的值;
(2)若对任意的x≥0,有f(x)≤kx2成立,求实数k 的最小值.

