活用“1”的代换解题

邱芳忠

（江西省信丰县第七中学）

“1”的作用在高中数学解题中不可小视，代换的得当，会给你的解题带来便捷，下面就以实例为据，来谈谈“1”到底能给解题带来多大的便捷？

一、“1”在比较两个实数的大小中的代换

评注：比较两个既不同底数与又不同幂的指数大小，除了要用到指数函数的单调性，还要引进“1”作为中间量，以起到纽带作用.

例2.比较两个数log2.13 与log3.12.9 的大小.

解：首先考查函数y=log2.1x，在x∈R+上是增函数，∵3＞2.1，∴log2.13＞log2.12.1=1. 然后考查函数y=log3.1x，在x∈R+上是增函数，∵2.9＜3.1，∴log3.12.9＜log3.13.1=1.综上所述，log2.13＞log3.12.9.

评注：比较两个既不同底又不同真数的对数的大小，除了要用到对数函数的单调性，还要引进“1”作为中间量，以起到纽带作用.

二、“1”在三角函数式化简与求值中的代换

评注：“1”代换tan45°后利用两角差的正切公式进行求值.

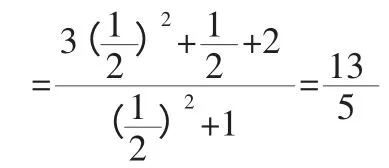
评注：“1”代换后首先要进行弦化切，然后再代值.

三、“1”在证明不等式中的代换

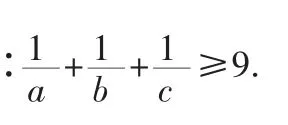
证明：∵a，b，c∈R+，且a+b+c=1,

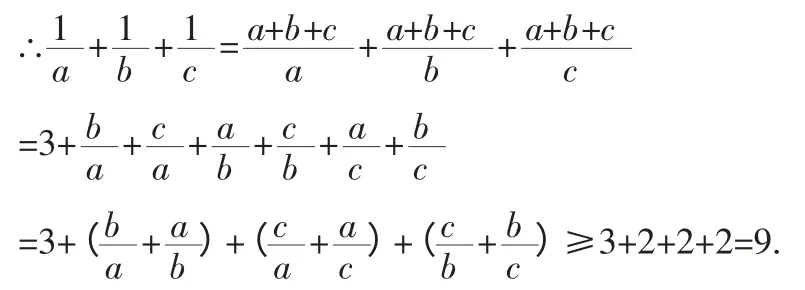
当且仅当a=b=c 时，等号成立.

评注：解答本题可以先使用“1”的代换，再转化使用重要不等式来证明.

四、“1”在求函数最值中的代换

故当x=4，y=12 时，（x+y）min=16.

评注：解答本题可灵活使用“1”的代换，再用基本不等式求得和的最小值.