利用错误资源提高课堂质量的方法

韦世奇

【关键词】错误资源 数学课堂 教学质量 教学策略

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2015）06A-0115-01

在新课程背景下，数学课堂教学提倡让学生自主、合作、探究学习，在此过程中，必然伴随着差错的出现和生成。当然，出错也并非绝对是坏事，关键是教师如何对待差错，如何有效利用教学中的错误资源，引导学生主动纠错，使课堂教学因差错而变得更精彩，并成为教学的生成点和增长点。

一、捕捉学生的认知错误，突破教学难点

教师在教学中不应只把焦点放在学生的正确解题上，也要有意识地关注学生的错误，善于在课堂上捕捉学生的错误。因为学生的一个错误见解往往便是学习中的难点或重点，也更能够激发学生的思维，促使更多的学生积极参与到学习活动中，亲历实践探究和构建知识的过程，使错误变为教学的亮点，促使课堂教学攻破难点，迸发出美丽的火花。

如在教学人教版七年级数学上册《有理数的加减混合运算》中“有理数的减法”时，明确了有理数的减法法则是“减去一个数等于加上这个数的相反数”，如算式“4-8”中“8”前面的符号“-”是减号，给学生留下了深刻的记忆。接下来学习“代数和”时，教师要求学生把“4-8”看成正4与负8之和，“-”则变成了负号。此时有的学生就会产生疑惑：到底把“-”看做减号还是负呢？假如学生无法消除这个疑惑，那么在计算时就可能产生错误。对此，教师在学生明确有理数减法法则的基础上，告知学生：有理数的减法可以改写为加法，如a+b-c=a+b+（-c），可以根据左边算式理解为a加b减c，还可以根据右边算式理解为a、b、-c的和（代数和），即代数和就是表示几个有理数相加的式子。因此，在代数和中，所有的运算都是加法，运算符号可以省略不写。这样，通过厘清知识背景及知识结构之间的关系，找出学生产生困惑的关键点，并进行有效解析，帮助学生消除困惑。

二、运用学生的错误，使错误成为学生思维发展的支撑点

教学时，学生因为缺少经验，容易产生认知偏差，从而出现错误。这时教师要善于对待学生的认知错误，站在学生的立场上看待学习中出现的认知错误，并将这一“错误”作为学生思维发展的支撑点，让学生在纠错的过程中发现问题、解决问题。

如在教学人教版七年级数学上册《有理数的加减混合运算》时，笔者出示一道题：59-（-20.4）-0.4=○.有学生这样计算：59-（-20.4-0.4）=79.8.对于学生出现的计算错误，教师不需要直接指导学生纠正错误，可以针对学生错误的计算方法，将题目改编为判断题：59-（-20.4）-0.4=59-（-20.4-0.4）=38.2，请学生判断正误。学生在判断正误的过程中，进行了自主探究。计算出错的学生在此过程中发现了错误，这时教师可以提问：“你是怎么发现错误的？”学生在教师的引导下，快速找到了计算错误的方法。学生经过探究、讨论，围绕不同的计算方法进行交流，从不同的视角考虑问题，在纠错的同时深化了对知识的理解。

三、制造错误，提升学生的数学能力

小泽征尔有一次到欧洲参加音乐比赛，在比赛时3次中断指挥，原因是他发现乐谱出错了。实际上，这是评委会设计的“圈套”，以此来考查指挥者的音乐素养。其实，在数学教学中，对于学生容易出错的知识点，教师也可以设置一些类似的“圈套”，将学生的错觉诱发出来，引导学生质疑、释疑，从而提高学生的数学素养和数学能力。

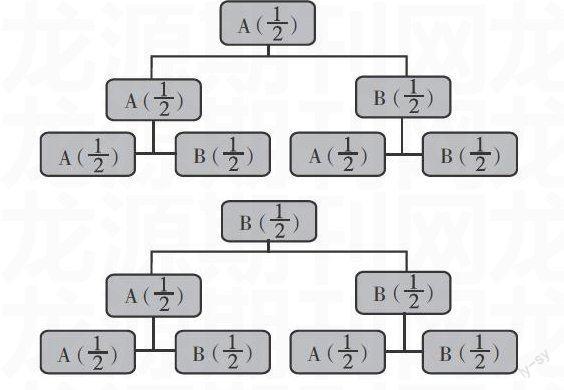
如教学人教版九年级数学上册《概率》，在学生掌握了计算概率的方法（如列举法、公式法等）后，笔者给出题目：一个家庭有3个孩子，求这个家庭中有2个男孩和1个女孩的概率。有的学生通过列举法很快得出结论，共有4种情况：女女女、女女男、男男男、男男女。对于学生的错解，教师可以设置“圈套”：除了列表法，还可以用什么方法计算？于是大部分学生开始用树状图求概率。如用A和B分别代表男孩和女孩，画出的树状图是：

通过画树状图得出结论：该家庭有2个男孩和1个女孩的概率为。在得出2种不同的结果后，教师故意不语。学生思考片刻后就会知道，第一种计算方法错了，因为虽然出现的男孩和女孩的情况只有4种，但每一种出现的可能性是不同的，忽略了概率的可能性这一特征。而用树状图的解法才是正确的。通过这样有意设置一些“圈套”，让学生解错题目，这对于他们深刻理解知识点是十分有益的，也有利于提高学生的数学素养。

“错误”是数学教学中的动态生成，教师要善于抓住“错误”资源，引发学生思维，在剖析交流中构建知识，在纠错中获取知识，深化学生对知识的理解。

（责编 林 剑）