“三策略”促进小学生数学符号意识的形成

苏巧真

[摘 要] 《全日制义务教育数学课程标准（2011版）》把培养学生的符号意识作为核心概念提出来，其重要性可见一斑. 本文提出了促进小学生数学符号意识形成的三个策略：多元表征，丰富学生的符号语言；多向转换，加深学生对符号的理解；多方运用，感悟符号的优势，以此促进学生数学符号意识的形成.

[关键词] 表征；转换；运算；推理

英国著名数学家罗素说：“数学是什么？数学就是符号加逻辑. ”数学符号以其简洁性、方便性、美观性将复杂的数学语言加以浓缩，用来表示数学概念、数学定理、数学公式和数学表达式，并解决问题. 数学学习很大程度上依赖于对数学语言和数学符号意义的把握. 《全日制义务教育数学课程标准（2011版）》把培养学生的符号意识作为核心概念提出来，其重要性可见一斑. 那么，在小学数学教学中如何促进学生符号意识的形成呢？笔者结合教学实践谈几点看法.

■ 多元表征，丰富符号语言

《全日制义务教育数学课程标准（2011版）》指出，“符号意识”主要是指能够理解并运用符号表示数、数量关系和变化规律. 这是从符号表征的角度对学生的符号意识培养提出的要求. 因此，在教学中，我们应积极创设各种机会，让学生用自己喜欢的方式来表征数学对象，如概念、公式、规律、定律等. 在小学阶段，学生的思维以形象思维为主，逐步向抽象思维过渡，因此，我们在促进学生符号意识的形成时，应遵循“从具体事物→个性化的符号表示→学会数学地表示”的符号化表征过程. 在创设问题情境时，应与学生的生活经验和已有知识经验相结合，所设问题要接近学生的最近发展区，这样，更能引起学生的共鸣，引发学生积极地投入学习. 如教学“用字母表示数”时，教师在黑板上写上“小明”二字——

师：你们猜，小明几岁？

生1：10岁？11岁？9岁？……

生2：▲岁.

生3：a岁.

师：你们是怎么想的？

生4：我们都不知道他的具体岁数，所以我想用一个字母或一个图形来表示.

师又在黑板上写上“小刚比小明大15岁”，

师：你们猜，小刚几岁？

生5：x岁？b岁？……（师板书）

生6：小明的年龄+15.（师板书）

生2：▲+15.（师板书）

生3：a+15.（师板书）

师：你觉得哪一个更好？

生7：▲+15，a+15更好，因为这两个式子比x岁、b岁更能表示小刚和小明之间的年龄关系.

生6：▲+15，a+15更好，因为这两个式子比“小明的年龄+15”更简洁.

师：是的，在数学学习中，我们不仅可以用字母表示数，还可以用含有字母的式子表示数量、数量关系.

上述案例中，教师创设了“猜年龄”的情境，这样的情境一方面接近学生实际，另一方面，极大地激发了学生的学习兴趣，学生在“猜”中自觉地使用图形、字母等个性化的符号表示“小明的年龄”，用文字、字母、含有字母的式子表示“小刚的年龄”，在“辩”中学生清晰地发现，“（▲+15）岁、（a+15）岁”比“x岁、b岁”更能看出小刚和小明之间的年龄关系，比“小明的年龄+15”更简洁，从而体会到用字母表示数量、数量关系的优越性. 在整个教学过程中，学生经历了从简单到复杂、从具体到抽象的符号表征过程，体现了学生学习的个性化，丰富了学生的符号语言，为学生的符号表达、符号运算和符号思维打下了良好的基础. 经历这样的学习过程是培养学生良好符号意识的关键.

■ 多向转换，加深符号理解

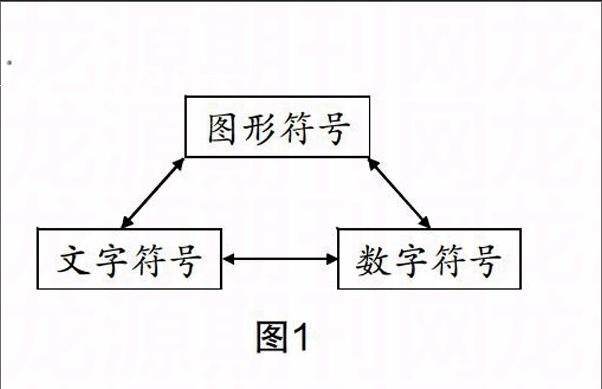
每一个数学符号都有它特定的含义，理解每一个数学符号的具体含义是促进学生符号意识形成的基础，也是培养学生符号意识的基本目标之一. 《全日制义务教育数学课程标准（2011版）》指出，“符号意识”主要是指能够理解并且运用符号表示数、数量关系和变化规律. 这一要求包含两层意思，一是“理解”（即“懂”符号），二是“运用”（即“用”符号）. 那么，“用”的前提是“懂”，只有感悟、理解符号表示的数、数量关系和变化规律的含义，才能做到正确运用，这就要求我们在教学中除了引导学生用多种方式表征数学对象外，还要引导学生在表征的基础上进行多种符号间的转换，以加深对符号的理解. 依据学生学习认知的规律. 在小学中、低年级，数学学习大部分运用的是图形符号、数字符号、文字符号，如数字的认识、简单的运算、概念等，教师在教学中要根据学生的认知规律引导学生对这三种符号进行互译（如图1），以加深对符号的理解.

■

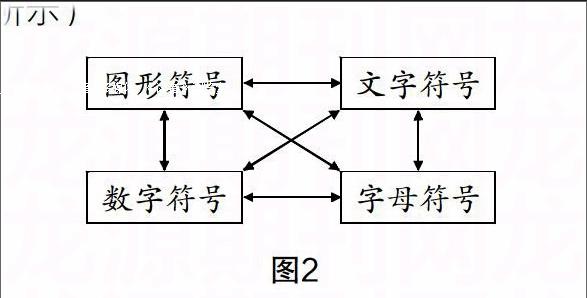
如教学二年级“乘法的初步认识”时，教师出示“花生图”，这是图形符号，教师引导学生把看到的信息表达出来：“5个花生，每个花生都有4颗仁”，这是文字符号；再引导学生根据意思用一个算式表达出来，这是数字符号；在学生建立对乘法认识的基础上，可出示数学乘法算式，让学生画图或编题，这是从数字符号向文字符号或图形符号的转换. 通过三种符号的互相转换，能加深学生对符号的理解. 在高年级学习中，增加了字母符号，从五年级的“用字母表示数”起，意味着代数学的开始. 用字母表示数量、数量关系对学生来说比较难，因此，在教学时，教师要从具体到抽象，先引导学生从文字表征、图形表征过渡到符号表征，当学生理解用字母表示数量、数量关系后，再出示如“4x”“5+a”“a+b-c”式子，让学生编生活中的数学问题. 如此，学生又经历了从字母符号向文字符号的转换，在这样的转换过程中，学生加深了对符号的理解，加深了数学与生活的联系. （以上过程如图2所示）

■ 多方运用，感悟符号的优势

《全日制义务教育数学课程标准（2011版）》指出，“知道使用符号可以进行运算和推理，得到的结论具有一般性. ”从中可以发现，培养学生的符号意识主要强调两条：一是知道符号可以像数一样进行运算和推理，二是知道通过符号运算和推理得到的结果具有一般性. 可见，发展学生的符号意识离不开让学生经历符号的产生、运用、推广、建模等过程. 知识只有运用于实践才能发挥它真正的作用，因此，在教学活动中，教师应积极引导学生主动运用数学符号进行运算、推理，经历符号化过程，领悟数学符号的抽象性、简洁性、模型性，感受数学符号系统的统摄性、优越性. 例如，教学“圆”时，教师经常呈现这样的题目：两个圆的半径之比是2 ∶ 3，则它们的直径之比是（？摇？摇？摇 ），周长之比是（？摇？摇？摇 ），面积之比是（？摇？摇？摇 ）.

生1：它们的直径之比是（2 ∶ 3），周长之比是（2 ∶ 3），面积之比是（4 ∶ 9）.

师：你是怎么想的？

生1：先分别求出两个圆的直径、周长、面积，再分别化简比.

生2：我觉得他的方法太麻烦了. 我是假设两个圆的半径分别是r和R，因为r ∶ R=2 ∶ 3，所以d ∶ D=2r ∶ 2R=r ∶ R=2 ∶ 3，C■ ∶ C■=2πr ∶ 2πR=r ∶ R=2 ∶ 3，S■ ∶ S■=πr2 ∶ πR2=r2 ∶ R2=4 ∶ 9.

生3：我们还发现了两个圆的半径之比、直径之比、周长之比是一样的，面积之比是半径之比的平方.

师：对于这三个同学的方法和发现，你有什么想说的？

生4：我觉得分别计算直径、周长、面积再化简的方法太麻烦了，我刚才也是这样算的，由于中间环节错了，结果错了.

生5：我觉得第二个同学用字母运用公式进行推导的方法比较好，不用大量计算，而且还让我们发现了长度之比和面积之比的规律.

以上教学，从具体到抽象，学生通过具体的数字计算，以及借助符号进行运算、推理的演算，两相对比，不仅得出两个圆的半径之比、直径之比、周长之比、面积之比的规律，还感悟到了用符号进行运算、推理的简洁性、优越性，感悟到了结果的一般性.

值得一提的是，在学习的起始阶段，让学生将字母看做已知数并进行运算或推理是比较困难的，但只要长期坚持，教师有意识地引导，相信学生主动运用符号进行表达、运算、推理的意识会逐渐提高.

总之，学生数学符号意识的形成并不是一蹴而就的，需要一个漫长的过程，这需要教师在教学中有意识地创造各种机会，让学生经历符号表征、转换、运算和推理的过程，让学生感受符号表达和符号思考的优越性，爱上数学符号，并形成自觉运用符号进行表达和思考的意识.endprint