且行且思考
——记一次说题比赛的历程
●徐建平 (海宁中学 浙江海宁 314408)
且行且思考
——记一次说题比赛的历程
●徐建平 (海宁中学 浙江海宁 314408)
傅瑞琦老师在文献[1]中提到“习题是数学教学活动中不可缺少的重要组成部分,通过分析解题思路、反思解题过程、拓展习题内容形式,加固学生的知识系统,加深对基本概念的理解,从而使概念完整化、具体化,形成完整、合理的认知结构”.从某种程度上说,数学教学的主体是习题教学,习题教学承载着数学教学兴盛的使命.如何将习题的功能更好地发挥,这成为教师教学研究的一个热点.说题,应运而生.作为一个新兴的教研活动载体,说题从构成(条件、结论分析)、解法、背景、拓展、作用等角度,展示试题的功能,从中揭示教学的内涵与本质.同时也为教师“如何恰当地在课堂教学中选择典型例题、在课后练习中选择习题、在考试中选择考题”提供了更多思考.本着学习提高的宗旨,笔者近日有幸参加了浙江省嘉兴市学科基地组织的首次说题比赛,一路走来,感慨颇多.
1 准备
题目 已知直线y=k(x+2)(其中k>0)与抛物线C:y2=8x相交于点A,B,其中点F为抛物线C的焦点.若|FA|=2|FB|,试求k的值.
拿到题目,首先要考证题目的来源.此题是2009年全国数学高考理科第9题,主要考查直线与抛物线的位置关系、抛物线的定义等知识,渗透了高中数学中重要的数形结合思想与函数方程思想.该题在各地的模拟试题中多次被引用,最近一次出现在2014年内蒙古自治区鄂尔多斯第2次仿真模拟考试中.
一个试题能多次被引用,说明其作为试题的价值不菲.本着这样的想法,笔者开始积极构建.
1.1 说构成,解题前的准备
阅读题目,分析构成,发现:一条直线y=k(x+2)(其中k>0)待定,一条抛物线C:y2=8x已知,2者之间的关系:相交.由此形成问题的焦点:交点与抛物线焦点的连线对应成比例.结论为探求该直线的斜率,即k的值.通过解读,确定本题以直线与抛物线的相对位置关系为主要考查点,以|FA|=2|FB|为出发点,考查直线的斜率.因此,可以确定|FA|=2|FB|是本题的题眼,那么如何利用好这一题眼,也就成了解决本题的关键.
1.2 说解法,展现问题解决多元化
通过对试题条件与结论的分析,了解试题的构成之后,笔者以题眼为基准,展开思考,构建解法.考虑到本题是一个解析几何问题,其典型性在于如何利用代数的方法解决;而其本身还是几何问题,几何有几何的特点.因此,在考虑本题的解法时,主要还是从代数与几何这2个角度试图呈现,实现数与形的统一.
1.2.1 代数解决,凸显解析几何通性通法
试题的教学与分析,要从学生出发,学会揣摩学生心理,贴近学生实际,这样的试题分析,才能获得更多学生的认可.从学生角度考虑,条件分析后发现是关于直线与抛物线相交的位置关系,则可从联立方程的角度去解决,这体现了解析几何问题解决的一贯思维——通性通法.

解法1体现了解析几何解决问题的一贯方式:代数方法解决几何问题,同时也是学生所能够并且也是最愿意接受的,因此要重点掌握.
再作思考,直线与抛物线相交,根据|FA|=2|FB|,可以得到2个交点相应坐标的对应关系,如果能够利用交点的位置来确定点B的坐标,那么利用两点求斜率公式就可得到k的值.
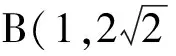
解法2的精妙之处在于:2条焦半径之间的比例关系与抛物线的定义发生了联系,再结合抛物线方程,建立了横坐标与纵坐标之间的联系,由此得到点B的坐标,获得问题解决的关键.
1.2.2 几何推理,彰显几何的简洁美
解析几何是几何的重要组成部分,其研究的方向是:根据已知条件,求解曲线的方程;根据给定的曲线方程,研究曲线的几何性质.以代数的方式解决几何问题,体现了几何的代数特征,凸显了数与形之间的联系.如此,是否可以回归几何,通过几何推理,寻求问题解决的方法?笔者结合抛物线的定义,通过添加部分辅助线后,豁然开朗!

图1
由此获得第3种解法:如图1,利用抛物线定义,转化|FA|=2|FB|得到|AM|=2|BN|,确定点A,B,P的位置关系.根据三角形中位线定理及等腰三角形的性质,结合图形确定点B的坐标,进而利用两点斜率公式计算得到结论.
3种解法各具特色:解法1体现了联立方程处理解析几何问题的通性通法;解法2则充分利用抛物线的定义,通过转化交点坐标之间的等量关系,确定点B的坐标,利用两点求斜率公式得到结论;而解法3则紧密联系几何性质,利用几何推理,结合三角形中位线性质得到等腰△OBF,并以此得到点B的坐标.问题解决相对简洁,计算也非常简单,这体现了几何的简洁美.如果说解法1和解法2是用代数的方式解决几何问题,彰显“解析”特性,那么解法3就是以“几何”的方式揭示“几何”本性.从数的角度计算几何,从形的方面思考几何,数与形在这里完美结合.得到上述解法后,还要能够分析优劣,加以理解,并最后形成对比,为后面的问题解决寻求更合适的方法.
1.3 说背景,寻根探源话变式、链接高考,呈现问题纵深性
对于任何一个试题,都要分解出其主要知识点、与教材的联系及其所要呈现的功能,以及可能出现的拓展、变式等状况.笔者在完成对解法的深入探究后,结合个人经验以及一些思考,尝试着从探源、变式、链接高考的角度对该试题进行深度挖掘.
1.3.1 寻根探源话变式
教学需要立足教材,以教材为纲,探寻试题与教材例习题之间的联系.分析试题知识点,发现人教A版选修2-1中第69页的例4是与之相关的问题:斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于点A,B,求线段AB的长.
试题以联立方程的形式,体现了直线与圆锥曲线相对位置关系的通性通法,同时也以数形结合的方式,突出了抛物线定义的重要性,这与本题的前2种解法不谋而合.
试题来源于教材,为教材服务,又要努力体现知识应用的可能性与全面性.本题通过对课本例题的改编,利用条件的改变,同时围绕直线与圆锥曲线位置关系的考查,体现了对解析几何问题联立方程这一通法的重要性.因此适当的变式有助于加深对问题及其解决方法的理解.

这些变式都是从直线与圆锥曲线的位置关系考查的通法——联立方程入手,体现了问题解决的一贯原则:由一题多变到多题一解.
1.3.2 链接高考,体现问题功能性
数学试题的功能在于承载数学知识的应用,也在于学生磨练之后在高考中能有所体现.本题作为2009年的全国高考题,重点考查了直线与抛物线的位置关系.从近几年各地高考和竞赛试题来看,抛物线的定义、基本几何性质、直线与抛物线的位置关系,甚至是一些与高等数学有关的初等数学问题解决,都是考查的热点与难点.如2012年安徽省、重庆市、北京市的高考卷,2013年浙江省、全国大纲版高考卷,2014年海南省、四川省的高考卷,2014年重庆市高考卷在选修模块中甚至以参数方程与极坐标的形式对其进行了考查.若将问题拓展到直线与圆锥曲线的位置关系,则这样的高考试题不胜枚举.
分析问题的条件与结论,寻找解决问题的方向,强化解题思路;拓展其各种变化,展示问题的全面性,拓宽学生问题研究的道路;挖掘问题深含的本质,寻求问题解决的通法,帮助学生知一题而达一类.试题是数学问题的重要承载工具,试题教学是高中数学教学一道重要工序.做好试题教学,有助于学生更好地学好数学.要做好试题教学,教师不能盲目追求数量而不顾质量,应该去教会学生思考,而且要善于思考.如何善于思考?一题多解、发散变式、寻踪探源是不变的追求.这既能让学生的思维获得迁移、发散和开拓,又能促使学生沟通知识点之间的联系,培养学生应用数学的能力.最后还要引导学生对比、小结,以此充分发掘试题潜能,提高数学应用能力,并在更大程度上培养学生思维的广阔性.
2 后记
参加此次比赛,笔者花了4个多小时准备,比赛时间为15分钟,一等奖的结果让笔者感到兴奋,有运气,也有诸多感慨.
2.1 说题需要勇气
本次说题活动,采取比赛前一天通过邮件公布试题的方式,因此,时间紧、任务重是本次活动的最大特点.而拿到试题的同时,恰逢学校有事,时间更加紧迫.白天准备基本没有可能,一时有放弃的准备.转念一想,活动难得,一则可以展示一下自己对试题的理解功底,二则还可以近距离观摩其他教师的说题内容,学习他们分析试题的经验,可以为自己在今后的试题分析方面积累素材与经验.于是抱着不怕丢人的想法,利用晚上的休息时间,抓紧准备,毅然参加了这次比赛.后来想想,勇气来源于对知识的渴求.
2.2 说题需要理解
2.2.1 理解数学是说好题的前提
众所周知,解数学题的本质是:要找到并且规范而简明地表述从题目已知条件到要求目标的一系列命题转化的道路.如何找到这条路,就需要对数学有比较深刻的理解.如何理解?笔者认为可以从3个角度进行探究:初级理解在于就题论题,从试题层面找到解决问题的方法,并能够顺利解决问题,甚至可以探寻一些一题多解问题;中级理解在于解题之后的反思,领会其中蕴含的数学思想方法,并能够比较解法的优劣,从而广开思路,另辟蹊径,探索最适合的解决问题的方法;高级理解在于不仅能够一题多解,还要能够通过搜集加工、自行设计一些问题,进行探究性学习,并作适当地归纳与提炼,以此达到“知一题而达一类”的效果.迪厄多内说:任何水平的数学教学的最终目的,无疑是使学生对他所要处理的数学对象有一个可靠的“直觉”.说题的目的,最终在于能够帮助学生找到这个“直觉”.
2.2.2 理解学生是说好题的关键
无论何种方式的教学,主题对象都是学生.教学方式的优与劣,直接体现在学生对知识的掌握程度.因此,要说好题,关键在于理解学生.贴近学生实际的说题,才是最成功的说题.关注学生,首先在于关注学生思维的最近发展区,让学生能够“跳一跳,碰得到”,将直线方程与抛物线方程联立,即让学生站在能够触到的地方,韦达定理是学生能够跳到的地方;其次在于关注学生的思维活动,要能够模拟学生的思考方向,优选解法,并尝试分析优劣,最终能够引导学生掌握一个最熟悉或最简单的问题解决方法.最后,教学的目的在于尝试培养学生的发散思维、求异思维、直觉思维和创新思维,从贴近学生的思维角度出发,编拟一些开放性的试题,通过变式,同化规律,使学生能够尝试掌握数学思维的规律、特点与方法,从而形成创新意识.
2.3 说题需要储备
2.3.1 资料储备
说题需要把试题的来龙去脉、多样解法、各类拓展以及与高考的相关性等比较详细地进行说明,同时,如果可以,还需要对试题所呈现的本质有所挖掘.教师不能仅凭借“百度”解决问题,平日资料的积累非常重要.出于对数学教学的热爱,笔者加入了数学群,收集了大量的资料,为本次说题活动的资料准备提供了很大帮助.通过查找资料,能够迅速找到与之有关的、相贴近的试题,同时还能从提供的试题解答中获取不同的解法和灵感.
2.3.2 能力储备
有了资料,其实还不够,还需要能够把这些资料有机地整合起来,这需要一定的能力.笔者在准备过程中,尽管解法呈现并不是很多,只有3种,但笔者从通性通法、定义以及数形结合的角度,从贴近学生实际的角度进行呈现,不仅将试题的功能展露无遗,而且可以使学生能够更好地接受,这是笔者比较满意之处.但也有不足之处,由于平时研究不够深入,对于试题的变式,只能就题论题,进行简单、浅层次地变化,而不能深入挖掘试题所蕴含的本源,同时对试题的功能总结还不够细致,这些都是在以后的教学、教研中需要加以改进的.
一路走来,幸福大于痛苦,且行且珍惜!
[1] 傅瑞琦.说题,让主题教研更精彩[J].中国数学教育,2012(3):45-48.
[2] 方家鸿.数学“说题”活动的过程与方法[J].中学数学教学参考,2010(4):33-35.
[3] 曹凤山.你能看出结果吗?—以一道例题的探究为例[J].中学数学教学参考,2011(9):37-39.
[4] 沈恒.说题谈题品题——一次说题活动预思考[J].中学数学研究,2012(9):3-5.
[5] 刘薇,沈恒.唯有漫江碧透,方可鱼翔浅底——一次说题活动给予的思考[J].中学数学,2015(4):70-72.
[6] 高红志,孙兰香.怎样理解数学[J].沧州师范专科学校学报,2004,20(3):23-24.
——作业改革探索与实践

