从一道课本例题推广

●章礼抗 (浮山中学 安徽枞阳 246736)



从一道课本例题推广

●章礼抗 (浮山中学 安徽枞阳 246736)

1 例题展现

现行高中数学人教A版4-4第33页有这样一道例题：

例1 已知O是直角坐标原点，点A,B是抛物线y2=2px(其中p>0)上异于顶点的2个点，且OA⊥OB，OM⊥AB并相交于点M，求点M的轨迹.

原解是用参数方程，这里笔者想用常规解法，并就此推出一般结论.

分析 设直线AB的方程为y=kx+m：若k不存在，设x=n(其中n>0)，则

由OA⊥OB，知

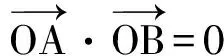
从而

x1x2+y1y2=0，

即

n=2p,

从而直线AB过定点(2p,0).

若k存在，则其与抛物线y2=2px联立，得

k2x2+2(km-p)x+m2=0.

现设A(x1,y1),B(x2,y2),则根据韦达定理知

由OA⊥OB，知

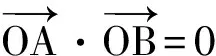
即

x1x2+y1y2=0，

亦即

(1+k2)x1x2+km(x1+x2)+m2=0,

则

解得m=-2kp，从而直线AB的方程为y=k(x-2p).易知该直线恒过点(2p,0).又因为OM⊥AB，所以点M的轨迹为

(x-p)2+y2=p2.

2 推广

原题中的曲线是抛物线，如果改为椭圆又如何？

分析 设直线AB的方程为y=kx+m:若k不存在，设x=n,则

由OA⊥OB，知

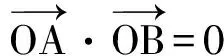
从而

x1x2+y1y2=0，

即

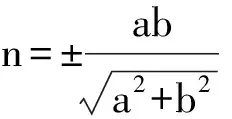
若k存在，则

从而 (b2+a2k2)x2+2a2kmx+a2(m2-b2)=0.

现设A(x1,y1),B(x2,y2),则根据韦达定理知

因为OA⊥OB，所以

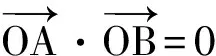
即

x1x2+y1y2=0，

亦即

(1+k2)x1x2+km(x1+x2)+m2=0,

从而

则

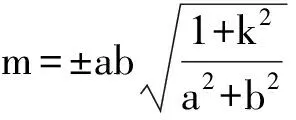
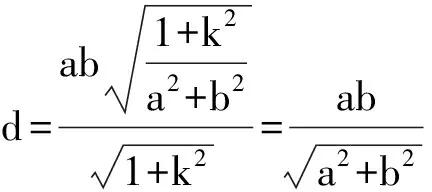
3 结论应用

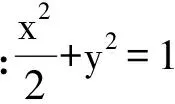
(2014年全国高中数学联赛天津赛区预赛试题)

分析 由以上结论知

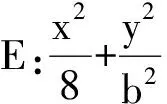
1)求b2的值；

2)求|AB|的取值范围.

(2013年河北省高中数学竞赛试题)

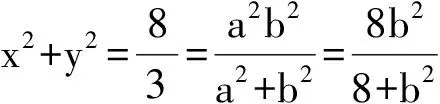
解得

b2=4.

2)设直线AB的方程为y=kx+m，则

从而

(4+8k2)x2+16kmx+8(m2-4)=0.

因为OA⊥OB，所以

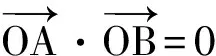
即

x1x2+y1y2=0，

亦即

(1+k2)x1x2+km(x1+x2)+m2=0,

解得

设A(x1,y1),B(x2,y2),则根据韦达定理知

从而

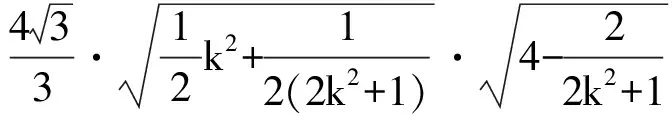
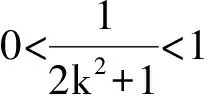
4 推广

原题中的曲线是抛物线，如果是双曲线又如何？

设直线AB的方程为y=kx+m:若k不存在，设x=n(其中n>a),则

由OA⊥OB，知

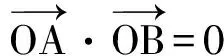
从而

x1x2+y1y2=0，

即

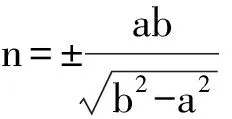
若k存在，则

从而 (b2-a2k2)x2-2a2kmx-a2(m2+b2)=0.

现设A(x1,y1),B(x2,y2),则根据韦达定理知

因为OA⊥OB，所以

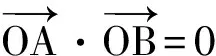
即

x1x2+y1y2=0，

亦即

(1+k2)x1x2+km(x1+x2)+m2=0,

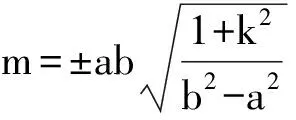
此时，直线AB的方程为

点O(0，0)到该直线的距离为

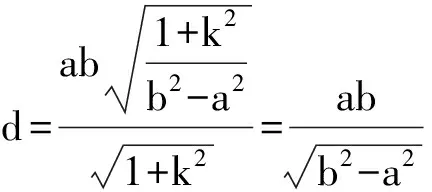
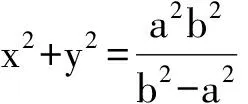
以上就是相关的推广与应用，如有不足之处，望读者给予批评指正.