论三角运算中的无理数

●沈 亚 (浙江师范大学数理与信息工程学院2012级教育硕士 浙江金华 321004)

●吕孙忠 (北京师范大学研究生院 北京 100875)



论三角运算中的无理数

●沈 亚 (浙江师范大学数理与信息工程学院2012级教育硕士 浙江金华 321004)

●吕孙忠 (北京师范大学研究生院 北京 100875)

文献[1]中针对一道“北约”自主招生的试题，得出了2个关于三角函数中的有理数和无理数命题如下：

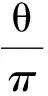
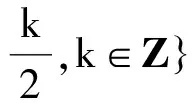
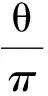
命题1和命题2分别讨论了余弦和正切的情况，那么正弦角的情况又是怎么样的呢？

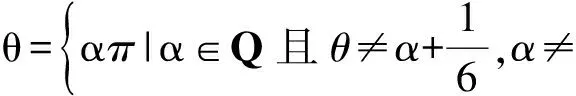
文献[1]中用了反证法，根据tan15°为无理数，证明了tan3°为无理数，那么tanθ和tannθ之间有什么联系呢？

推论1 若tanθ为有理数，则tannθ为有理数，其中n∈Z.

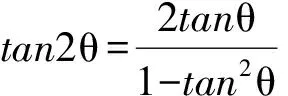
推论2 若tannθ为无理数，则tanθ必为无理数，其中n∈Z.

分析 用反证法证明.若tanθ为有理数，则根据推论1，可得tannθ为有理数，矛盾，故tanθ必为无理数.

分析 类似于推论1的证明，可用数学归纳法得到该结论.

推论4 若cosθ为有理数，则cosnθ为有理数，其中n∈Z.

分析 根据切比雪夫多项式展开

2cosnθ=(2cosθ)n+a1(2cosθ)n-1+…+

an-1(2cosθ)+an，

其中a1,…,an-1,an为正整数，可知，若cosθ为有理数，则cosnθ一定为有理数.

推论5 若cosnθ为无理数，则cosθ为无理数，其中n∈Z.

分析 用反证法证明.若cosθ为有理数，则根据推论3，可得cosnθ为有理数，矛盾，故cosθ必为无理数.

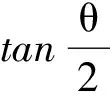
众所周知，kπ～k×360°，它在弧度制中是无理数，而在度的单位中却是一个整数.如果将单位转为度，那么在正弦、余弦和正切中，对任意θ∈(0°,90°)且θ∈Q，只有sin30°，cos60°和tan45°为有理数，在以度为单位的三角形中可得:

推论7 如果一个三角形的3条边都是有理数，且存在一个内角的度数为有理数，则该内角的大小只能是60°，90°，120°.

下面通过具体的例子来说明这些结论在解题中的应用.

例1 证明：tan3°是无理数．

(2014年“北约”自主招生试题)

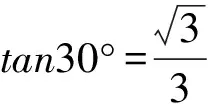
分析 对于问题1)，文献[3]中的证明技巧性非常强，过程比较复杂，现给出比较简单的解法.

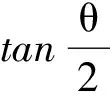
例4 如果一个三角形的3条边和3个内角的度数均为有理数，则该三角形一定是等边三角形.

分析 根据推论7，可知该三角形3个内角为60°，90°，120°之一，不妨设为A，B，C，则A+B+C≥60°+60°+60°，且A+B+C=180°，故A，B，C均为60°，即该三角形为等边三角形.

[1] 黄丽生.一道“北约”自主招生试题的探究与推广[J].中学教研(数学),2014(6)：28.

[2] 闵嗣鹤，严士健.初等数论[M].3版.北京：高等教育出版社，2005.

[3] 刘培杰.有理数与无理数的判定[J].中等数学,2015(3)：8-12.