一道考查“中点”的好题
●李玉荣 (金陵中学河西分校 江苏南京 210019)
一道考查“中点”的好题
●李玉荣 (金陵中学河西分校 江苏南京 210019)
线段的中点是几何图形中一个特殊的点,除了中点的概念外,依据《数学课程标准》和《义务教育标准教科书》,解题时常见的联想途径有:直角三角形斜边上的中线等于斜边的一半;三角形的中位线平行于第3边,并且等于第3边的一半;倍长中线构造全等三角形(或平行四边形)等.每年中考涉及中点的试题比比皆是,而2014年辽宁省本溪市数学中考第25题却让人眼前一亮,此题独具匠心、特色鲜明,中考复习时供学生练习事半功倍.
题目 如图1,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC+∠EAD=180°,△ABC不动,△ADE绕点A旋转,联结BE,CD,F为BE的中点,联结AF.
1)如图2,当∠BAE=90°时,求证:CD=2AF.
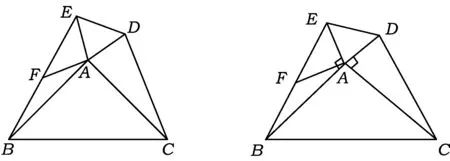
图1 图2
2)当∠BAE≠90°时,第1)小题的结论是否成立?请结合图1说明理由.
分析 此题由2个小题构成:第1)小题因为AF是Rt△ABE斜边上的中线,所以BE=2AF,然后通过△ABE≌△ACD即可得证;第2)小题∠BAE≠90°,如何利用中点是关键,显然无法直接使用,需添加辅助线,有以下2种思路(共5种证法):
思路1 构造三角形的中位线,延长EA至点H,使得AH=AE,根据三角形的中位线等于底边的一半,求得BH=2AF,然后证明△ABH≌△ACD,从而BH=CD,即可解决问题.
思路2 倍长中线AF,构造平行四边形得到AG=2AF,然后通过△ABG≌△CAD证得AG=CD,也能解决问题.
1)证明 如图2,当∠BAC+∠EAD=180°,∠BAE=90°时,∠DAC=90°.在△ABE与△ACD中,
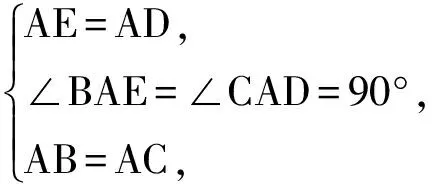
从而
△ABE≌△ACD(SAS),
于是
CD=BE.
因为在Rt△ABE中,F为BE的中点,所以BE=2AF,进而CD=2AF.
2)证法1 当∠BAE≠90°时,第1)小题的结论仍成立.如图3,延长EA至点H,使得AH=AE,从而AH=AE=AD,联结BH.因为∠BAC+∠EAD=180°,所以
∠EAB+∠DAC=180°.
又因为∠EAB+∠BAH=180°,所以
∠BAH=∠DAC.
在△ABH与△ACD中,
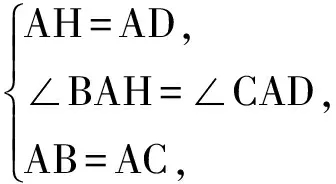
从而
△ABH≌△ACD(SAS),
于是
BH=CD.
因为EF=FB,AH=AE,所以
BH=2AF,
进而
CD=2AF.
以上是命题者提供的参考答案,笔者研究此题,另有收获:
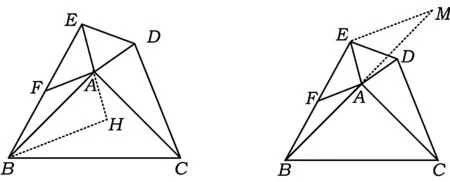
图3 图4
2)证法2 当∠BAE≠90°时,第1)小题的结论仍成立.如图4,延长BA至点M,使得AM=AB,则AM=AB=AC,联结EM.因为∠BAC+∠EAD=180°,所以
∠EAB+∠DAC=180°.
又因为∠EAB+∠EAM=180°,所以
∠EAM=∠DAC.
在△AEM与△ADC中,
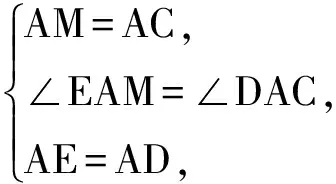
从而
△AEM≌△DAC(SAS),
于是
EM=CD.
因为EF=FB,AM=AB,所以
EM=2AF,
进而
CD=2AF.
2)证法3 如图5,将△ABE绕点A顺时针旋转,使AE与AD重合.因为∠BAC+∠EAD=180°,所以
∠DAB′+∠DAC=∠EAB+∠DAC=180°,
从而点B′,A,C在一条直线上.又因为AB=AC,BF=FE,所以CD=2AF.
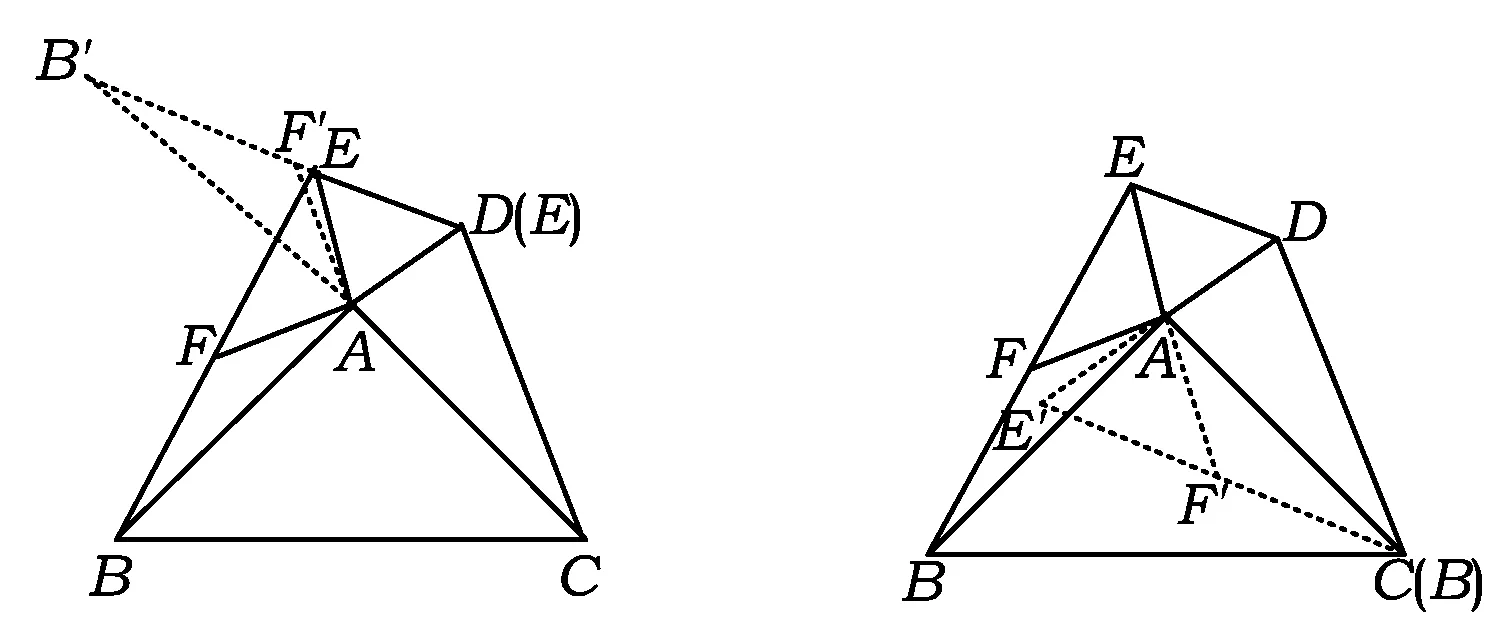
图5 图6
2)证法4 如图6,将△ABE绕点A逆时针旋转,使AB与AC重合.因为∠BAC+∠EAD=180°,所以
∠E′AC+∠DAC=∠EAB+∠DAC=180°,
从而点E′,A,D在一条直线上.又因为AE=AD,EF=FB,所以CD=2AF.
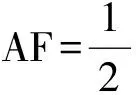
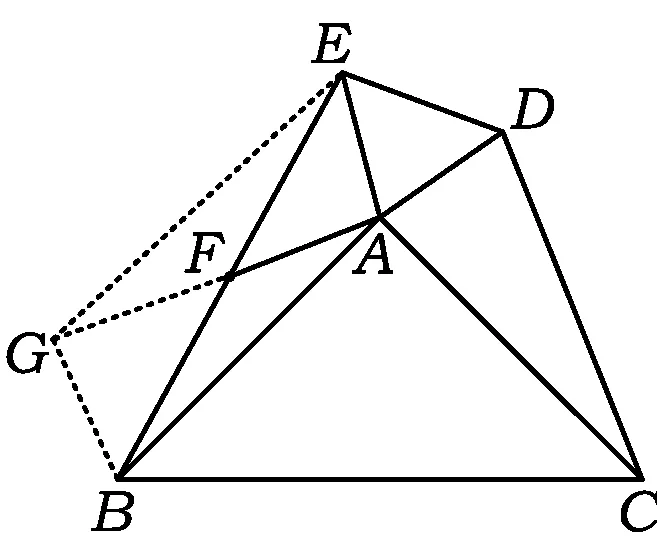
图7
2)证法5 如图7,延长AF至点G,使得FG=AF,则AG=2AF.因为EF=FB,所以四边形ABGE是平行四边形,从而
BG=AE=AD,GB∥AE,
于是 ∠EAB+∠GBA=180°.
因为∠BAC+∠EAD=180°,所以
∠EAB+∠DAC=180°,
进而
∠GBA=∠DAC.
在△ABG与△CAD中,
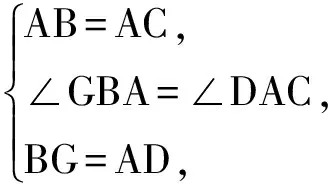
从而
△ABG≌△CAD(SAS),
于是
AG=CD,
故
CD=2AF.
评注 要证CD=2AF,可倍长AF转化为证明2条线段相等.在教学实践中,大多数学生想到的是这种方法,通过证明△AEF≌△GBF,得出BG=AE=AD,但接下来如何证明,部分学生一筹莫展,需教师提示利用△AEF≌△GBF,得出GB∥AE(还可得内错角相等),从而∠EAB+∠GBA=180°,再与已知∠EAB+∠DAC=180°沟通,才能完成证明.尽管过程稍显繁琐,但作为常用的一种思路、方法,教师还是应该予以肯定.
拓展 从证法5可得∠FAB=∠ACD,“求证:∠FAB=∠ACD”是一道更有挑战性的习题.
从题目的命制看,试题旨在考查全等三角形的判定与性质以及与“中点”相关的2个重要定理.第1)小题的特殊角“∠BAE=90°”,应用“直角三角形斜边上的中线等于斜边的一半”不难证明CD=2AF;第2)小题的非特殊角“∠BAE≠90°”,先让学生猜想“第1)小题的结论是否成立?”,体现了从特殊到一般的数学思想,但条件改变了,对结论的证明无法机械地套用第1)小题的方法,需创新思维,联系与中点相关的辅助线是解题的关键.
从题目的解法看,方法的多样性是一道题目被认为是“好题”的重要条件之一.证法1~4从不同的角度构造出三角形的中位线解决了问题,尤其是证法3和证法4,利用旋转的不变性,将AF与CD这2条分散的线段巧妙地集中在一个三角形中,利用“三角形的中位线等于第3边的一半”直接得解,解题过程极为简洁,而证法5所采用的“倍长中线”则是众多教材上一道典型例(习)题揭示的基本图形,具有极高的利用价值,常有意想不到的收获.此题与学生日常学习“获得基本的数学活动经验”密切相关,给考生留下了广阔的思维空间,彰显了《课程标准》中“不同的人在数学上得到不同的发展”的理念,不愧是一道耐人寻味的考查“中点”的好题,值得中考复习中选为例题或习题,并将探究解法的教学过程展开,尽可能地让学生主动参与解法探究,提出各自解决问题的策略,进行比较和讨论,丰富数学活动的经验,提高数学思维的水平.
著名数学家波利亚说过:一个专心、真正备课的教师能够拿出一个有意义但又不太复杂的题目,去帮助学生完善问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的领域.我们期待2015年中考有更多这样的好题问世,为数学试题的“大花园”增色添彩.
[1] 郝新武.一道习题的探究与反思[J].中国数学教育:初中版,2012(5):25-27.

