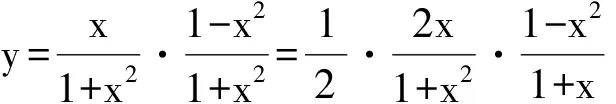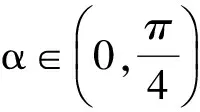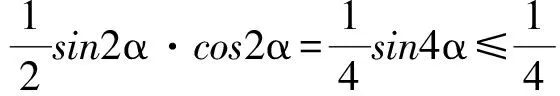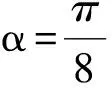类比联想寻思路 三角换元巧解题
●许书军 刘少平 邹 鹏 (仙桃市第八中学 湖北仙桃 433000)
类比联想寻思路 三角换元巧解题
●许书军 刘少平 邹 鹏 (仙桃市第八中学 湖北仙桃 433000)
数学竞赛中许多代数问题,结构复杂,变元较多,学生往往陷入盘根错节的变量关系之中,难以理清头绪,找不到解题切入点而无从下手.这时如果借助题目显现的某些特征和关系,从分析问题的整体结构出发,类比联想相关三角公式和恒等式模型,适时采用三角换元,不仅能简化题设信息,使隐性条件显性化,而且可以沟通变元之间的关系,使繁杂的代数问题转化为简单的三角变换问题而快捷获解.
1 类比联想sin2θ+cos2θ=1
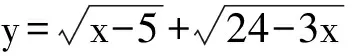
( )
(2011年全国高中数学联赛四川赛区初赛试题)
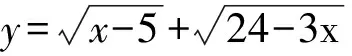
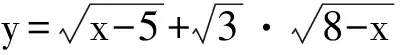
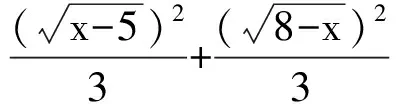
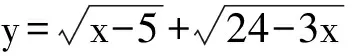
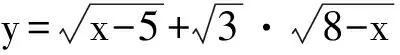
又
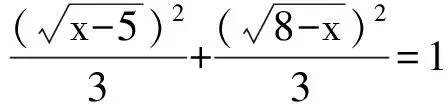
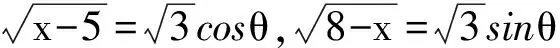
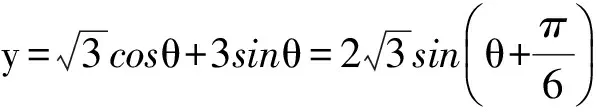
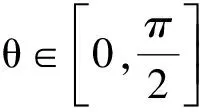
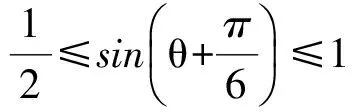
从而
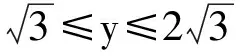
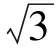
例2 已知正实数a,b满足a2+b2=1,且a3+b3+1=m(a+b+1)3,求m的取值范围.
(2012年全国高中数学联赛湖北赛区预赛试题)
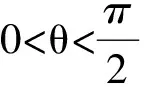
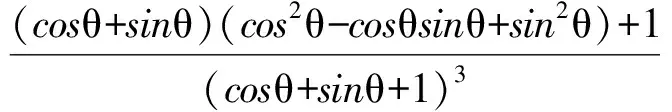
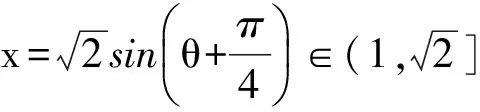
且
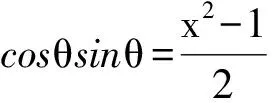
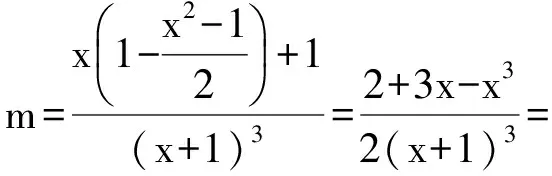
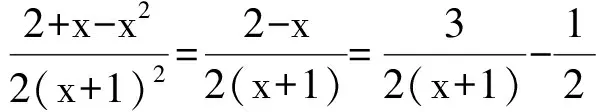
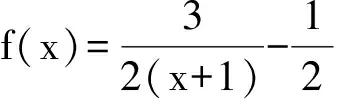
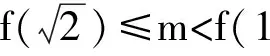
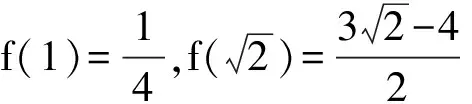
2 类比联想sin2α+(cosαsinβ)2+(cosαcosβ)2=1
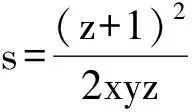
(2010年湖北省高中数学联赛试题)
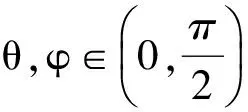
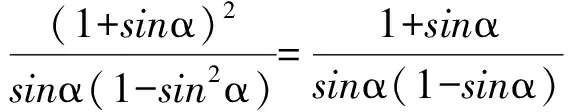
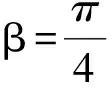
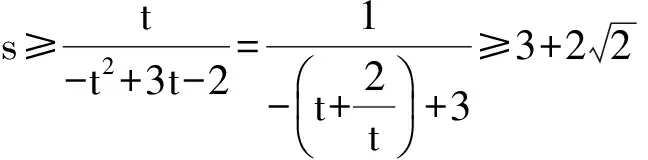
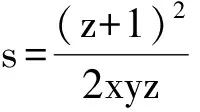
例4 已知实数x,y,z满足x2+2y2+5z2+2xy+4yz-2x+2y+2z+11=0,求x+2y+3z的取值范围.
(2011年世界数学锦标赛青年组试题)
分析 初看本题,似乎无从下手,但若将已知条件配方,则
(x+y-1)2+(y+2z+1)2+(z-3)2=3.
联想到 sin2α+(cosαsinβ)2+(cosαcosβ)2=1,
就可以用三角函数模型来表达求解了.
解 将已知条件配方可得
(x+y-1)2+(y+2z+2)2+(z-3)2=3,
令
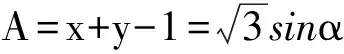
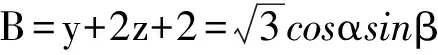
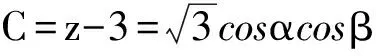
于是D=x+2y+3z=A+B+C+2=
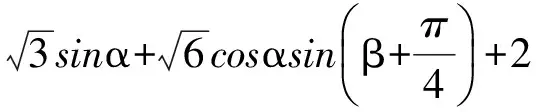
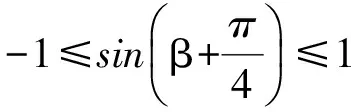
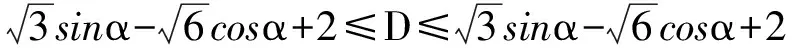
即
3sin(α-γ)+2≤D≤3sin(α+γ)+2,
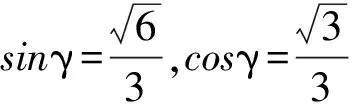
sin(α-γ)≥-1, sin(α+γ)≤1,
所以
-1≤D≤5,
故x+2y+3z取值范围为[-1,5].
3 类比联想sec2θ-tan2θ=1
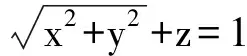
(2010年北京大学自主招生试题)
分析 将已知条件变形可得
(1-z)2-y2=x2.
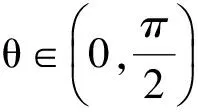
解 由题设易知0 (1-z)2-y2=x2. xy+2xz=x2tanθ+2x(1-xsecθ)= 从而 故 例6 若x2+2xy-y2=7(其中x,y∈R),求x2+y2的最小值. (2013年浙江大学自主招生试题) 解 由x2+2xy-y2=7,得 (x+y)2-2y2=7. an>an-1>…>a2>a1>a0, 因此数列{an}是单调递增数列. 解 由已知条件知 a+c=(1-ac)·b, 故 β=α+γ, 2cos2α-2cos2(α+γ)+3cos2γ= cos2α+1-cos(2α+2γ)-1+3cos2γ= 2sinγsin(2α+γ)+3cos2γ≤ 2sin2γ+3cos2γ=3-3sin2γ+2sinγ= 又xn+1=x1,得 tan2nθ=tanθ, 得 于是原方程组的解为 例10 设x,y,z均为实数,且x+y+z=xyz,求证: 分析 待证等式中的每一个分式与正切的二倍角公式相类似,已知等式和待证等式分别是3项和与3项积,自然联想到三角中的恒等式tanA+tanB+tanC=tanAtanBtanC(其中A+B+C=kπ,k∈Z),进一步观察题设与结论可以发现,只要令x=tanA,y=tanB,z=tanC,此题就容易解决. 因为 x+y+z=xyz, 所以 tanA+tanB+tanC=tanAtanBtanC, 从而 tanA+tanB=-tanC(1-tanAtanB), 即 亦即 tan(A+B)=tan(-C), 得A+B=kπ-C,即 A+B+C=kπ(其中k∈Z), 故 2A+2B+2C=2kπ(其中k∈Z), 于是tan2A+tan2B+tan2C=tan2Atan2Btan2C, 例11 设x,y,z∈R+,x+y+z=1,求证: 证明 由x+y+z=1联想到在△ABC中, 故待证式等价于 事实上,在△ABC中,由琴生不等式可知 故待证式成立. 例12 若a>1,b>1,ab-(a+b)=1,求a+b的最小值. 解 由ab-(a+b)=1,可得 (a-1)(b-1)=2, 解 注意到 通过以上解答和分析,我们发现:充分关注条件与结论的结构特征,展开类比联想,探索沟通条件与结论间的联系,采用恰当的换元法,就能左右逢源,迅速找到问题解决的突破口.这不仅培养了学生的思维能力,开发了学生的智力,而且还提高了学生解决问题的能力.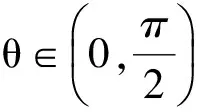
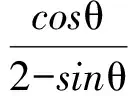
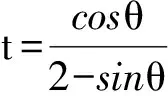
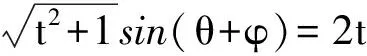
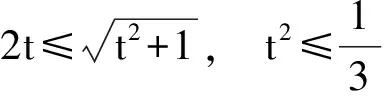
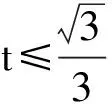
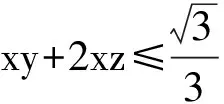
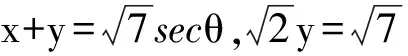
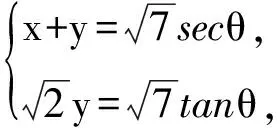
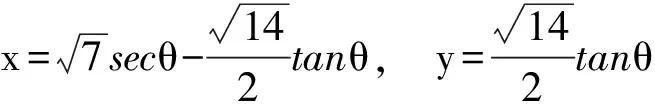
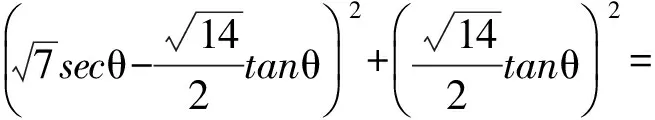
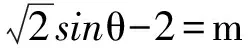
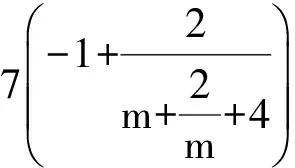
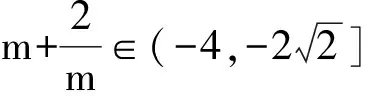
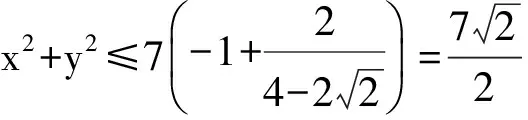
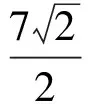
4 类比联想
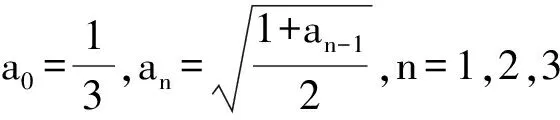

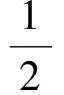
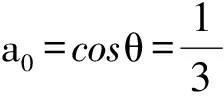
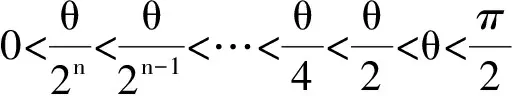
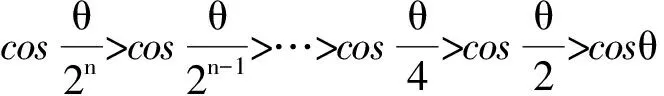
5 类比联想
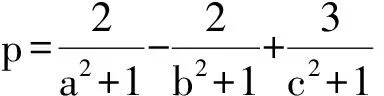
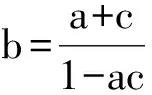
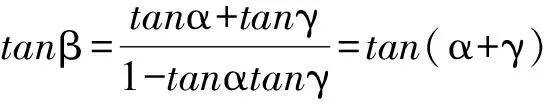
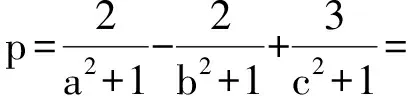
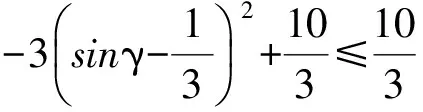
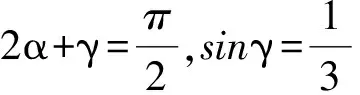
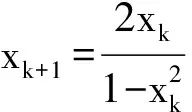
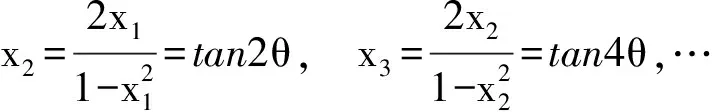

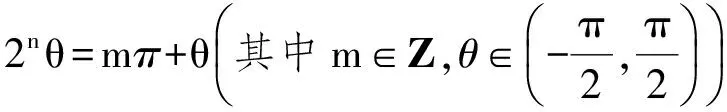
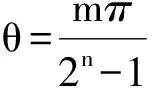
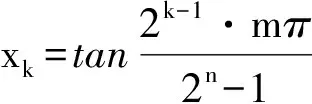
6 类比联想tanA+tanB+tanC=tanAtanBtanC
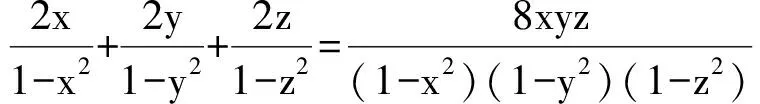
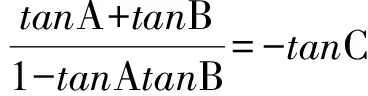
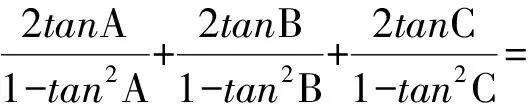
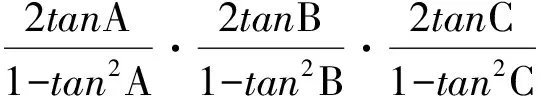
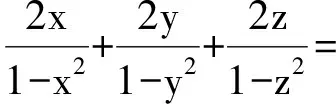
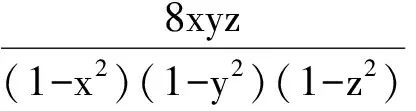
7 类比联想
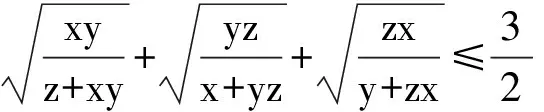

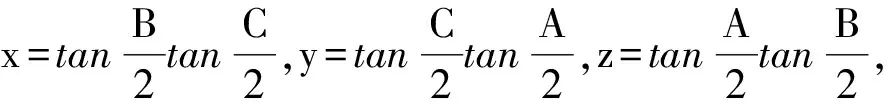
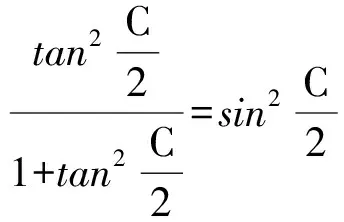
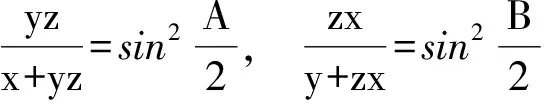
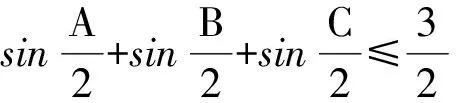
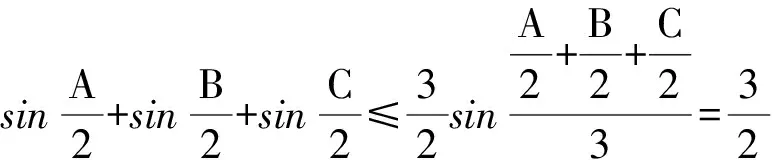
8 类比联想tanθcotθ=1
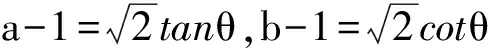
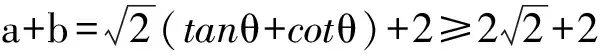
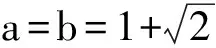
9 类比联想万能公式