当“预设”遇上“生成”——听“极化恒等式”同课异构有感

●金雪峰 (湖州市第二中学 浙江湖州 313000)



当“预设”遇上“生成”
——听“极化恒等式”同课异构有感

●金雪峰 (湖州市第二中学 浙江湖州 313000)

笔者参加了浙江省湖州市专业成长数学协作体举办的高三数学复习课课堂教学研讨会.在听了2节同课异构的“极化恒等式”后，笔者强烈感受到了“预设”与“生成”的较量.现将一些粗浅的认识和感悟与各位同仁交流.

1 片段展示

师1：请几位同学讲讲想法.

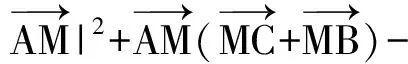
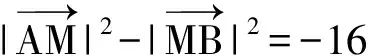
还有其他想法吗？

生2：运用刚才所学的极化恒等式知识,可知

师1：好，还有其他方法吗？

生3：建坐标系.

师1：对，我们来演示一下，以BC为x轴、BC的中点M为坐标原点建立直角坐标系，则B(-5，0)，C(5，0)，A(x,y),从而

又因为

所以

x2+y2=9，

因此

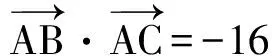
当然,如果要小题小做的话，直接取A(0,3)即可.

师1：好，下面我们看刚考过的一模题(PPT展示):已知a·b=0，向量c满足(c-a)·(c-b)=0,|a-b|=5，|a-c|=3，则a·c的最大值为______.

(学生思考片刻，没太大反应.)

师1：我们用极化恒等式来试试.如图1,因为

而

代入即可.再请大家思考，如果求最小值呢？

片段2 引出极化恒等式，解释极化恒等式的优点，再进行训练.

师2：学了这个工具，再回看例1,如何用这个工具求解？

(学生被简单的解法触动了.)

师2：我们把这道题“秒杀”了，如果是在高考时就节省了很多时间.

生：呵呵呵……

图1 图2

师2：试着用这个工具求解例2:

生：用极化恒等式

师2：很好，用的是极化恒等式的简化版.请再思考线段PO上2个端点的情况.

生：点O固定，点P在正方体表面运动，因此

从而

师2：很好，再仔细想想，为什么这2道题能顺利用极化恒等式解决呢？

生：等式右边的2个长度中有1个是定值.

师2：很好,再看一道题试试:

师2：例3虽然也是向量的数量积，但是和极化恒等式有区别，起点不相同，怎么办？

师2：我们发现极化恒等式使用环境是向量的数量积，要注意向量起点要一致.再看例4:

师2：这2个长度都在变，怎么处理？

生：最大值-最小值……

师2：极化恒等式在2个长度中有1个为定值的情况适用，当2个长度都变化时，只要有规律也是可以解出来的……

2 2节课的比较与思考

2.1 比较

2位教师的课堂“预设”相似，他们均从题根出发，引出极化恒等式，再运用这一工具分析以往的向量应用小题巩固拓展.但2位教师“预设”中对“生成”留有的“弹性空间”不同，对课堂“生成”的重视程度不同，导致课堂氛围和效果大不相同.如师1在生1回答了向量分解的方法、生2回答了利用“极化恒等式”解决的方法后，没有见好就收，而是又提问“有无其他方法？”在生3回答建立坐标系后，提示“还有坐标法”.之后，给学生1分钟时间思考，1分40秒完成坐标法的解答.笔者猜想师1的“预设”是想多提供一种解法，多一条思路，但从学生角度理解，容易造成混乱.新方法“极化恒等式”还没理解透彻，坐标法也没想到，教师已将3种方法跃然于黑板，感叹之余，恐怕更多地产生了对数学的敬畏之心，而不是亲近感.师2引导学生由问题1提炼形成“极化恒等式”，再通过后续问题引导学生逐步理解、体会、运用“极化恒等式”，整个过程的安排由浅入深，逐层递进，拾级而上.从学生的“最近发展区”出发，符合认知规律.在课堂中师2密切关注学生的课堂“生成”，借助“生成”顺水推舟，充分肯定了学生创造的“简化版极化恒等式”等宝贵的“生成”资源,提高了学生的学习热情.学生反应敏捷，效果非常好.虽然师2没有使用多媒体，但是他的教学容量大于使用多媒体的师1.

2.2 思考

从2节课的比较中发现注重课堂“生成”的师2教学效果比较好，但不是说可以抛开“预设”只仰仗“生成”.“预设”和“生成”孰重孰轻，如何驾驭它们呢？笔者的观点是：“预设”像大树的主干，“生成”犹如枝叶.离了主干枝叶何存，离了枝叶枯木一棵.

2.2.1 “预设”是“主干”

所谓“预设”就是预测和设定，也就是教育工作者从学情和教材出发单方面的教学设想.不仅包括怎样创设情境，如何层层递进、如何设问、如何剖析等，还包括为课堂“生成”预留弹性空间.“预设”的作用是提出教学目标，确保学生的基本知识和技能的落实，因此课堂教学离不开预设.“预设”的原则是以学情为准，为“生成”预留弹性空间.2位教师虽然都作了不错的预设，但是师1的“预设”不够充分.首先,例1的练习难度没有梯度，学生跳一跳“摘”不到，也就没了学习兴趣;其次,师1没有预设过学生如果没有掌握好例1该怎么办的问题，没能为“生成”留白.师2的预设更有动态空间，以学生“生成”为本，先是从2012年浙江省数学高考理科第15题开始，在使用一般和极化恒等式2种方法的对比中让学生体会新知识的快捷方便.很多学生被简单解法触动.在这样的背景下再由浅入深，逐层递进地安排后面的问题.从处理三角形中的雷同题到略有变化的解析几何题，让学生训练巩固，体验此类方法的价值，体会数学习题中的变式和迁移.他的“预设”考虑到了学生的热情和“生成”，为学生的“生成”铺平了道路.

2.2.2 “生成”是“枝叶”

“生成”是课堂教学的生长和重新建构.因为教师并无预知未来的能力，再精心的预设也不可能预知课堂上的每一个意外.这时课堂生成就有重要的价值，需要教师机智地抓住这些信息，去粗取精.如果根据“生成”分析大部分学生并未按预设方向前进，说明“预设”不符合学情，只能改变“预设”来适应“生成”:如果“生成”是一个好的意外，那么借题发挥能更快达成目标;如果“生成”是个不好的意外，那么先解决学生的疑惑，再把它整合到“预设”中，不要过度发挥.如此有了“生成”的实时监控，教师才能能顺着学生的思维，及时调整教案，把握教学过程的轻重缓急，引导学生获取一个个可喜的“意外”，让课堂焕发“动态的活力”.师1看到了学生的生成，但没引起重视，严格按照预设进行,“生成”尚未形成又提供了很多新方法，非但没能激发学习兴趣，反而打击了学习新知的热情,课堂效果“大打折扣”;师2没有固步自封于原有的教案圈圈之中，卸下包袱，带领学生一起探究,不拘泥预设，迎来未曾预约的精彩——“简化版极化恒等式”.可见有了“生成”的实时监控，课堂“预设”更接地气，更趋完美.

因此“生成”是调节课堂节奏、教学进度的一个根本标准，而并非是“预设”有没有“进行到底”.在动态生成的课堂上，教师要善于激发学生的学习需求，要懂得放手让学生自主探索与合作研究.有时，这种研究、探索才是课堂教学动态生成的“根源”.

3 结束语

高效课堂应该“预设”和“生成”相辅相成，相互促进.“预设”时为“生成”留白，“生成”时不忘“预设”初衷.如此课堂教学的“树”才能“主干粗壮，枝叶繁茂”.

[1] 刘霞.浅论课堂预设与生成[J].教师教育,2013(7)：23-24.

[2] 李冉.高效课堂：预设与生成的完美结合[J].北京教育:普教版,2013(8)：45.