用迭代法求公切线

赵小香

用迭代法求公切线

（广西师范大学数学与统计学院 广西·桂林 541004）

摘 要 根据牛顿切线法求方程的根的思想，结合2008年数学建模A题，运用迭代法求两凸集（椭圆）的公切线，算法简洁实用，可操作性强。并证明了算法对公切线的收敛性和收敛速度。

关键词 迭代法 公切线 凸集分离 数学建模

中图分类号：O182 文献标识码：A DOI：10.16400/j.cnki.kjdks.2015.05.014

Seek Common Tangent with the Iterative Method

ZHAO Xiaoxiang

（School of Mathematics and Statistics， Guangxi Normal University，

Guilin， Guangxi Normal University， Guilin， Guangxi 541004）

Abstract According to Newton's equation of the tangent method the root of thinking， combined with mathematical modeling A title in 2008， using the iterative method for two convex sets （oval） common tangent， the algorithm is simple and practical， workable. And proved common tangent algorithm convergence and convergence rate.

Key words iterative method; common tangent; separation of convex sets; mathematical modeling

0 引言

随着计算机加入科学研究的行列，迭代算法作为计算机能执行的有效算法，在解决实际问题中起着越来越重要的作用。区间二分法、牛顿法等都是经典的迭代法。

2008年高教社杯全国大学生数学建模竞赛甲组A题《数码相机定位》问题的一种解决思路是通过求公切线交点的方法来确定圆心。而求两个椭圆（或R2内任意有界闭凸子集）的公切线就可以用迭代算法来实现。尤其是在离散（椭圆由相片给出，而相片只能分解为离散的像素点）的情况下，迭代算法更加适合于计算机的实现。

1 数码相机定位

08数模A题的数码相机定位问题给出了标靶以及标靶在相机中的像，如图1、2要求设计算法求出相片中圆的圆心，以建立像坐标系到世界坐标系的点点对应，从而完成系统标定。具体题目见文献[1]。

图1 标靶       图2 标靶在相机中的像

公切线交点的方法是指根据直线的像还直线的原理，作圆A与圆C、圆A与圆E的外公切线，如图3，四条切线有四个交点，构成正方形，正方形对角线交点即为圆A的圆心。在相片中，只需求出变形后的圆A与圆C、圆A与圆E的外公切线，即可确定圆心。图4。

图3 标靶中的公切线 图4 像中的公切线

所以问题可转化为设计算法求两圆的外公切线。而本文主要研究如何用迭代法来求两圆的公切线。

2 外公切线算法

求两个椭圆（或R2内任意有界闭凸子集）的外公切线的迭代算法，具体操作步骤如下：

（1）对给定的两个椭圆A、B，分别任意给出一条切线和，切椭圆A，切椭圆B，两切线在两圆的同侧，且只与一圆线切，如图5。

图5 初始切线            图6 第一次迭代

（2）过和的交点做和的角平分线，如图6。

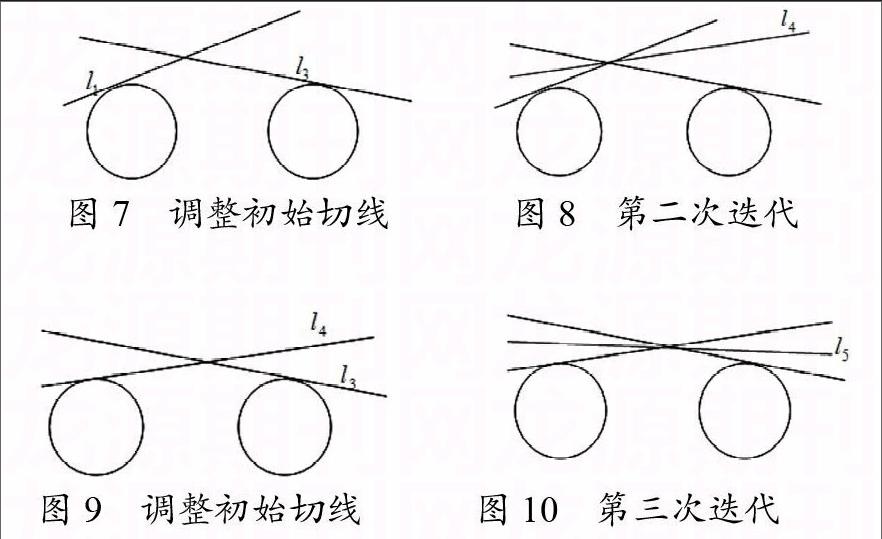
（3）将平移至与圆相切，如果能与两圆都相切，即为所求公切线，则停止。若不能与两圆都相切，将平移至较近的圆，并取代与该圆相切的直线。如图7，平移后与圆B相切，且用取代。

（4）过和的交点做和的角平分线，如图8。

（5）将平移至于一圆相切，如果能与两圆都相切，即为所求公切线，则停止。若只能与一圆相切，将平移至该圆，并取代与该圆相切的直线。如图9，平移后与圆A相切，且用取代。

图7 调整初始切线 图8 第二次迭代

图9 调整初始切线 图10 第三次迭代

（6）过和的交点做和的角平分线，如图10，重复以上过程。

（7）当与两圆相切或与两圆距离达到足够小的精度时，停止。

在实际操作中，做两直线的角平分线可改为取两直线斜率之和的一半为斜率做直线，这样并不影响收敛性和收敛速度。

定理1 上述步骤给出的平分直线的斜率收敛于两椭圆的外公切线的斜率。且收敛速度为（）。

证明：设的斜率为，的斜率为，两椭圆公切线的斜率为，<<则的斜率 = ，∣∣≤。

不妨设取代了，则根据的取法，有<<。那么的斜率 = ， 从而∣∣≤≤。

同理，∣∣≤， ≥2。

即上述步骤给出的平分直线的斜率收敛于两椭圆的外公切线的斜率。且收敛速度为（）。

3 算法实现

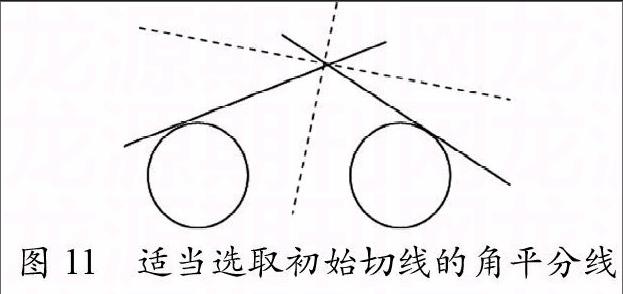
在上述迭代法实现应用过程中，我们一般适当调整坐标系，使得所求公切线的斜率大致在0.5到1.5之间，并选择合理的初值，使得每次所选的角平分线是两椭圆同侧的直线，而不是另一条将两圆分开的角平分线，如图11。同时，也可减少计算精度带来的误差。

图11 适当选取初始切线的角平分线

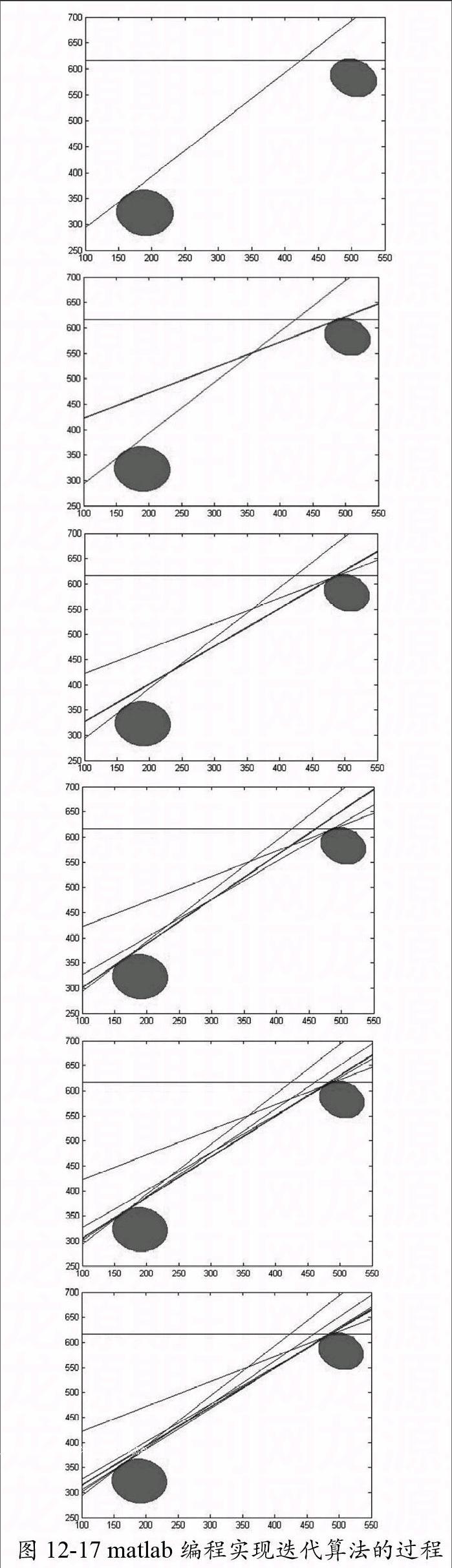
以08数模A题为例，我们给出用matlab编程实现上述迭代算法的具体过程。

按照上述方法继续迭代，直到达到允许精读。由图12-17 可以看出，当迭代四五次以后，就已经相当精确。

值得注意的是，同样的思路可以用来求内公切线，进而可以将两个凸集分离。

图12-17 matlab编程实现迭代算法的过程

参考文献

[1] 华东师范大学数学系编.数学分析（上）第四版[M].北京：高等教育出版社，2010.7.

[2] 全国大学生数学建模竞赛.http：//www.mcm.edu.cn/.2008.9.