波利亚“怎样解题”表的应用与评价
涂敏 汤强
【摘要】有研究表明,一个失败的解题者与成功的解题者,其最大的差异在于采用的解题策略.著名的数学教育家波利亚提出了一整套解题的方法,形成了“怎样解题”表,本文将结合四川省南充市2013年的一道中考题来谈谈该表中解题策略的使用以及对其策略的使用进行评价.
【关键词】怎样解题;解题表;解题策略
一、解题训练对于学生的意义
自古以来我国就是数学解题的王国,解题训练是我国数学教育的鲜明特色.解题之所以受到如此的重视,是因为它对学生而言具有重要的意义,具体而言可以分为外部意义和内部意义两个方面.
1.外部意义主要体现在它是学生应对考试的法宝.随着新课程改革的实行,“以人为本”的素质教育的呼声越来越高,以人为本的思想主张减轻学生负担,还学生自由.但这里的以人为本并不是我们很多学生和家长所理解的那样,认为学生做题越少越好,而是要注重提高学生的解题技巧和策略.如今,考试仍然是压在学生头上的大山,为了拿到好的分数,学生还是要拼命地练题.这样解题策略就尤为重要,只有真正地提高了学生的解题策略,才会在尽量减少学生练题负担的同时让学生拿到理想的分数.
2.内部意义主要体现在它有助于学生数学思维能力的形成.这种能力不仅对学生今后解题有益,而且可以使学生的整体数学学习能力得到提高.如果将解题简单地理解为一种程序性知识,认为只要记住足够多的知识点,将每种题型都练到练熟,就可以在考试中得心应手,那么就大错特错了.这种题海战术对于应对简单题也许管用,但是对于那些需要复杂操作技能的难题,解题策略和过程性知识就显得尤为重要了.
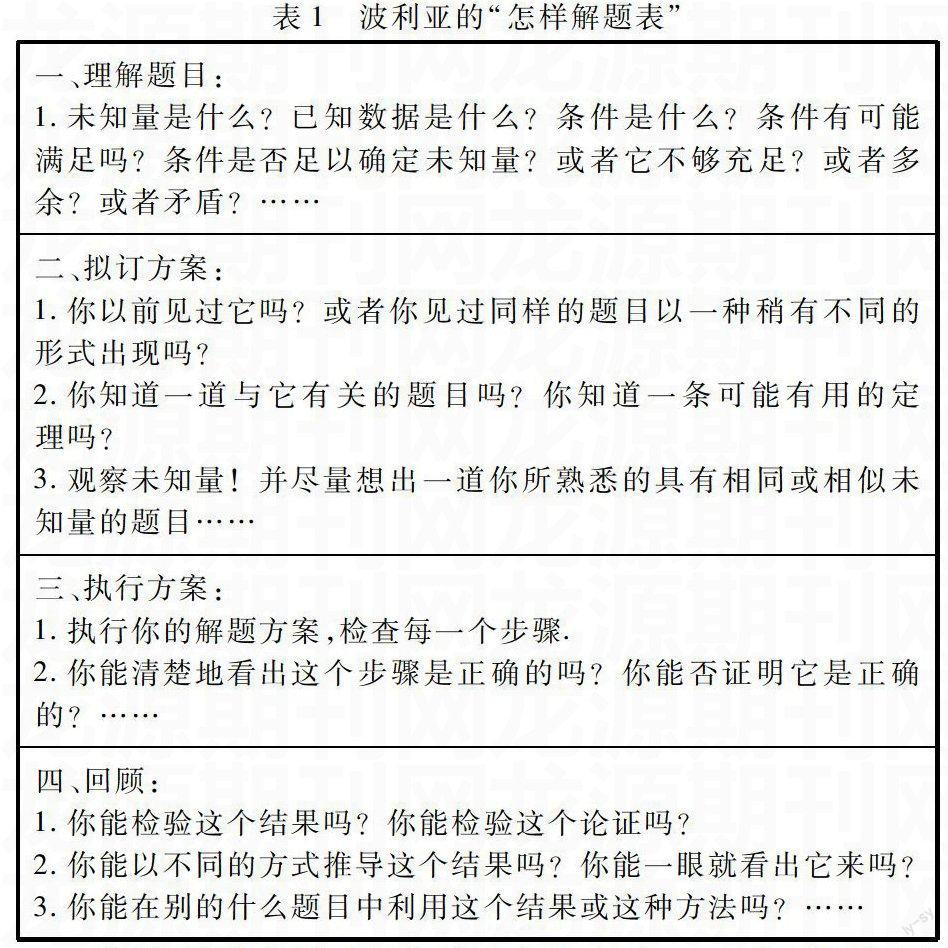
二、波利亚“怎样解题表”的简介
说明:他将解题过程大体上分为四步.一、理解题目:主要是找到已知量、条件和所求这三个部分;二、拟订方案:主要是找出已知量和未知量之间的联系,并进一步制订初步的解题计划,在这里波利亚重点提出了在解题时要注意题目与以前做过的相关题目之间的联系;三、执行方案:是将第二步计划的方案付诸实践,并检验每一步是否正确;四、回顾:这一步是在整个题目做完之后对解题的每一步骤的反思,这种反思不仅是对解题具体过程的回顾,还要重新梳理整个题目解答过程中的思路,总结解题中的经验和教训,这样学生就会在思维的更高层次上进行再概括,促使思维进入理性认识阶段,由会一题到会一类,达到事半功倍的效果.
三、波利亚“怎样解题表”解题策略的评价
所谓解题策略,就是解题者为了提高解题的效果和效率有目的、有意识地制定的有关解题过程的复杂的方案.而波利亚提出的这一套解题策略对于数学解题无疑是非常有效的,他的策略主要体现在分步实施和不断反问两个方面.
1.分步實施的策略.分步实施的策略实质上是解题者对解题过程的一种计划.他将解题的过程分为四步,每一步都有相应的任务,这样做的好处是可操作性强.具体地分为四步,这样学生在解题之前,就会条件反射式地想到“四”这个数字,然后回忆每一步要完成哪些任务.另外,这四步虽然各有其不同任务,但是它们在逻辑上具有整体性、顺序性和连续性的特点.整体性体现在四个步骤之间并不是孤立存在的,而是相互紧密联系的有机整体.顺序性体现在四个步骤是按照一定顺序进行的,前一步是后一步的前提条件,每一步都具有严密的逻辑顺序.连续性体现在每一步都是相互联系的,它们环环相扣,缺少了其中任何一步都难以成功解题.
2.不断提问的策略.波利亚的解题表中有很多问题,而且这些问题都是解题者在解题过程中对自己的反问.这种反问有三方面的意义.其一,这一系列公式化的指导意见是对解题者的提醒.提醒解题者尽量提取可用到的解题资源,这里所谓的解题资源包括两部分,一部分是外显的由题目所给的已知数据和条件,另一部分是内隐的解题者大脑中的数学经验(以往的解题经验、相关公式定理、相关相似题目的解题方法等等).很显然这些解题资源对于题目的解答是至关重要的.当解题者面对纷繁复杂的已知条件和数据时,有时候并不清晰哪些是有用信息,哪些是多余信息;并不清晰具体哪些信息是用于解答第一问的,哪些信息是用于解答第二问的;并不清晰哪些是直观信息,哪些是隐含信息.而通过不断地反思,不断辨析,可以使这些信息明朗化.其二,不断反问是解题者对自己解题过程的一种监控.这种监控既能确保所采取的措施是否可行,又是对解题过程的监控,随时掌控着离目标的距离,这样不断地向目标靠近,最终达成解题目标.其三,不断反问还可以起到调节的作用.当发现解题过程中遇到障碍时,立即采取补救措施,采用其他方法进行尝试,通过不断地修正最终找到通往目标的正确之路.
【参考文献】
[1]G.波利亚.怎样解题[M].上海:上海科技教育出版社,2007.
[2]朱丹.试论数学解题教学的重要性[J].
[3]鲍建生,周超.数学学习的心理基础与过程[M].

