巧妙渗透解题策略无痕发展数学思维研究

丁妮妮

摘 要：解题策略是一种思维模式，它以解题过程为载体，能使学生在参与探究过程中逐步获得解题思维的发展。文章从常见的逆向思维策略、假设策略、图形辅助策略三个方面研究巧妙渗透解题策略，无痕发展学生的数学解题思维。

关键词：数学思维；解题策略；逆向思维；假设策略；图形辅助

中图分类号：G622.479；G623.5 文献标志码：A 文章编号：1008-3561（2016）33-0024-02

培养学生的解题策略是数学教学的重要任务，由于解题策略蕴含于解题过程中，单纯的理论说教无法让学生有效掌握解题技巧，导致学生的解题能力无法得到发展。因此，教师要结合解题过程渗透解题策略，从而无痕发展学生的解题思维。

一、巧妙渗透逆向思维策略，无痕发展数学思维

由于长期受到应试教育的影响，一些教师习惯用自己的解题思维引导学生，导致解题过程不够灵活，学生的思维严重受限。因此，新课标倡导学生运用逆向思维进行解题，逆向思维解题是数学解题中的一种重要策略。所谓的逆向思维是学生创新思维的表现，它强调从未知条件出发，进行题目反思，从而为已知条件和未知条件找到突破口，帮助学生打破思维禁锢，提升解题能力，实现无痕发展数学思维。

例如，小明玩弹珠，他买了一盒弹珠，第一天玩掉了这盒弹珠的一半还多1个，第二天玩掉了剩下的一半还多1个，第三天玩掉了剩下的一半还多1个……以此类推，到第五天时，盒中只剩下1个弹珠（这天，小明没有再玩弹珠了）。问：小明买的这盒弹珠共有多少个？按正常的思维模式，学生必须从弹珠的总数去考虑，而弹珠的总量不知，假设总共有x个弹珠，那么第一天小明玩掉1/2x+1个，第二天（1/2x+1）/2+1个，会推导出一个比较复杂的式子，而且很难计算出答案。而逆向思维就可以为本题找到突破口。根据分析，最后一天剩下1个珠子是关键点，结合已知条件推想，每天玩掉一半还多1个，由剩下的1个可以推导出第四天是玩掉3个，因为一半还多1个，剩下1个加上还多的一个就是2个，2个乘以2就是4个，然后再向前推就可以找到答案。可见，逆向思维分析法能够有效提高学生的解题效率。又如，新新电脑专卖店上午卖出笔记本30台，中午进货50台；下午又卖出15台，店里还有72台。问：新新电脑店原有笔记本多少台？仔细分析题目可发现已知条件经过了三次变化。如果直向思维会陷入思维困境，而逆向思维却能找到突破口。根据已知条件，可通过三步实现逆向思维推导：一是电脑店最后现存笔记本72台，要计算下午卖出15台前的数量，应该用加法，即：72+15=87（台）。二是中午进货50台，店里原来的笔记本台数必须用减法计算，即：87-50=37（台）。此步得知在进货之前，电脑店里有笔记本37台，但问题还没有解决完，因为早上卖出笔记本30台，所以必须再逆推一步。三是电脑店在上午卖出30台之前就是电脑店原来的笔记本台数了，即：37+30=67（台）。综合列式为：72+15-50+30=67（台）。可以说，通过逆向思维推导法能够有效解决已知变量不断变化的问题。由此可见，逆向思维方式解题策略能让学生突破直向思维的局限性，使学生的思维更灵活。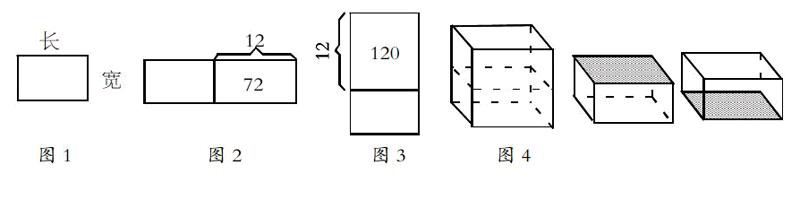

二、巧妙渗透假设解题策略，无痕发展数学思维

假设法也是一种比较常见的数学解题策略，主要适用于一些比较难的问题。学生通过分析已知条件，并建立与未知结果相关的数量关系，从而让数学问题变得更加透明，以此达到提高学生解题效率的目标。假设法要求学生能够结合已知条件和假设的未知变量，分析出题目中的数量关系，并建立起相应的等式。这样，能突破思维盲区，提高解题解题效率。

例如，陶瓷厂制作一批陶器，原计划用18天制作完成，实际每天比计划多制作了50件，按此速度制作了12天，超过原计划产量 240 件，陶瓷厂原计划制作多少件陶器？仔细分析题目，原条件中并无每天制作多少件的已知条件，且也无法得知实际的制作件数。如果按照原有的数量关系进行解题会比较困难，但运用假设法刚好可以将未知条件用假设代替出来。由于原计划制作的件数不知道，用x进行假设，然后顺着题意进行推理，（x÷18+50）×12=x +240，然后利用方程解法求出答案是1080件。此题用假设法的优势在于当第一个求知条件假设之后，学生的思维会变得清晰。上题是条件假设，在解决问题时，还可以应用情境假设。例如，松鼠爸爸采松子，晴天每天采20个，雨天每天采12个，它一连8天采了112个松子，问这几天中晴天、雨天各是多少天？晴天、雨天的天数不知道，教师可以渗透情境假设法，假设8天全是雨天，则松鼠爸爸采松子的数量为：12×8=96个。而题目中给出的实际松子数量为112个，相比于假设条件下，松子数量少了112-96=16个。为什么会减少？晴雨天每天相差的松子数为：20-12=8个，则实际的晴天天数为：16÷（20-12）=2天，雨天就是6天了。可以说，针对不同的题目，情境假设能够有效解决已知条件与未知结果之间无直接联系的问题。因此，教师应该重视引导学生能够灵活应用假设解题策略完成数学题目，并在解题中无痕发展数学思维。

三、巧妙渗透画图解题策略，无痕发展数学思维

直观手段是变抽象为形象的重要策略，教师可以结合一些题目巧妙渗透画图策略，使学生借助图形理解题意，并找出相对应的数量关系，借生动、直观的图形将数学原理、概念形象化、简单化，从而使学生能够真正明白各数学变量之间的联系，有效提高解题效率。

例如，有两个自然数a和b，如果把a增加12，b不变，积就增加72；如果a不变，b增加12，积就增加120，求原来两数的积。由于题目给出的条件比较复杂、抽象，因而在解决时可将借助长方形图将题目条件转变成为因数与积的关系。首先，可先画出一个长方形，a表示长，b表示宽，如图1。其次，当a增加12，b不变，积就增加72，如图2。a不变，b增加12，积就增加120，如图3。最后，通过观察图形就能够得出：原长方形的长为120÷12=10，原长方形的宽为72÷12=6，那么原长方形的长和宽的积为10×6=60。借助图像，相比于直接解题法更加有效率、迅速。

上述题目主要是借助平面图找到解题的方法。另外，也可以借助立体图完成解题。例如，把一个正方体切成两个长方体，表面积就增加了8平方米。原来正方体的表面积是多少平方米？学生的想象力有限，单纯依靠文字无法找到突破口。如何帮助学生更好地理解已知条件，并到解题方法呢？教师可以引导学生画图辅助思考（图4），题中给出的条件是表面积增加了12平方米，实际上是增加 2个正方形的面，每个面的面积是12÷2=6（平方米）。原正方体是6个面，即表面积为6×6=36（平方米）。可以说，通过直观图能让学生在观察中建立更多的感性认知，有效提高解题速度。除此之外，教师还可以引导学生借助线段图、分析图、表格图、思路图等多种图形去理解题意，从而提升解题速度。同时，教师还要结合不同的题意渗透灵活的画图解题方法，以提升学生解题的敏捷性，最终促进解题能力的发展。

四、结束语

总之，解题策略是学生知识结构中最核心的组成部分，影响着学生解题技巧和解题方法的掌握。而要想丰富学生的解题策略，就需要教师抓住学生的逻辑思维特点，巧妙结合不同的题型渗透解题策略，使学生在感性的认知中找到解题方法，并不断形成新的解题策略，从而达到综合能力提升的目的。

参考文献：

[1]王庆春.例谈小学教学的几种经典解题策略[J].数理化解题研究，2016（26）.

[2]魏雪峰，崔光佐.小学数学问题解决认知分析、模拟及其教学启示——以“异分母相加”问题为例[J].电化教育研究，2013（11）.

[3]吴锦文.对解决问题的策略的一点体会、感悟[J].数学学习与研究，2011（12）.