乘法分配律的教学实践与思考

郑德华

【摘要】 乘法分配律的学习是个难点，可以从孕伏中渗透、意义中建构、练习中达成、拓展中提升加以有效突破.

【关键词】 乘法分配律；渗透；意义；练习；拓展

小学阶段学习了加法交换律、结合律，乘法交换律、结合律，乘法分配律，简称“五律”，是以例题的形式呈现学习的；而“两性质”即减法性质与除法性质是结合在练习中渗透的. 这“五律”“两性质”是学生进行简便运算的依据. 纵观多年来的教学实践，学生对于乘法分配律的学习始终是个难点，好些学生总是跨不过这道门槛. 因此笔者多年来一直在探究思考，如何让学生能自主地跨过学习乘法分配律这道门槛，让学习真正地发生. 我反复尝试着、反思着，摸索出了比较可行的方法，现撰写成文，以期能起到抛砖引玉的效果.

一、孕伏中渗透

乘法分配律的学习是个难点，突破难点的方法之一，就是做好前期孕伏渗透，以便分散难点. 可以从以下方面进行渗透.

1. 学习两位数乘一位数时孕伏渗透

比如，学习12 × 3，结合情境图、列竖式计算，让学生理解把12分成10 + 2的和，先算2个3的积，再算10个3的积，最后把两积合起来. 关键再引导一步让学生把算式表示出来，得出算式是：12 × 3 = （2 + 10） × 3 = 2 × 3 + 10 × 3.让学生对着算式读几遍，12 × 3等于2加10的和乘3等于2个3的积加上10个3的积，凸显这一环节，目的就是有意识地渗透乘法分配律的结构.

2. 学习混合运算时孕伏渗透

苏教版四年级上册学习乘加、乘减混合运算时，练习中已经安排形如这样的题组：

36 × 25 + 36 × 75，36 × （25 + 75）.

这里安排这样的题组练习，目的有二：其一是巩固混合运算的运算顺序，提高运算技能；其二就是编者有意识地孕伏渗透乘法分配律的知识，让学生通过练习，对比感知这样的两个算式是有联系的，是可以用等号连接起来的了解了编者的良苦用心，那么应该如何渗透呢？笔者是这样教学的：在学生观察这两个算式的基础上，先让学生猜想这两个算式的结果怎样，有的学生说相等. 接着让学生通过计算加以验证，原来两个算式的结果的确相等，用等号把两个算式连起来，齐读一遍. 最后引导学生通过乘法的意义加以解释为什么两道题的结果相等. 因为左边的算式表示25个36加上75个36，也就是（25 + 75）个36，即100个36，而右边的算式也表示100个36，所以两道算式的结果是相等的. 那么在计算这两道时，哪道算起来更方便呢？今后我们在计算36 × 25 + 36 × 75时第一步可以怎样改写呢？这就是下学期我们要学习的运算律.

3. 学习长方形的周长时孕伏渗透

学生在建构长方形的周长公式时，会出现长 × 2 + 宽 × 2，也会出现（长 + 宽） × 2. 这时教师就可以引导学生把（长 + 宽） × 2写成长 × 2 + 宽 × 2，让学生明白两者之间的联系. 为渗透乘法分配律的知识做好铺垫.

如果我们的老师能在这些知识的建构处有意识地引导、渗透，学生的前期学习中就具备有乘法分配律的影子，到真正学习乘法分配律时就不会感到陌生，有种似曾相识的感觉，学生接纳起来就容易得多了.

二、意义中建构

乘法分配律难就难在学生对乘法算式意义的不理解，学生中常出现这样的错误就足以说明这一点. 比如（30 + 2） × 16，有的学生是这样计算的：（30 + 2） × 16 = 30 × 16 + 2，只把30乘16，而2不乘16，说明学生对算式表示的意义不理解. 因此新知的教学要从乘法的意义入手，让学生从意义的角度来建构乘法分配律.

从例题中学生得出（6 + 4） × 24 = 6 × 24 + 4 × 24，让学生从意义的角度解释两个算式相等的理由，左边算式表示（6 + 4）的和个24，即10个24，右边的算式表示6个24加上4个24，也是10个24. 在学生提出“两个数的和乘一个数等于两个数分别乘这个数再求和”的猜想，学生举例验证这一猜想时，也让学生从乘法意义的角度来解释，观察众多例子归纳出乘法分配律的字母表达式（a + b） × c = a × c + b × c，仍让学生用乘法的意义加以解释，（a + b）的和个c可以写成a个c加上b个c；反过来a个c加上b个c可以写成（a + b）的和个c. 从初步发现（6 + 4） × 24 = 6 × 24 + 4 × 24，到学生提出猜想、举例验证、归纳规律，始终以乘法的意义为抓手，触及问题的实质，有效地避免了有的学生依葫芦画瓢，机械记忆， 只知其一不知其二.

三、练习中达成

练习是学生巩固新知、形成技能、发展思维的有力载体. 针对乘法分配律的特点、学生的易错点，笔者以教科书的练一练和练习十的练习为载体设计了四个层次的练习.

（一）基本练习

1. 在□里填数，在○里填上运算符号.

本题练习主要是让学生巩固乘法分配律的结构，从正用到反用，又从反用到正用，在这个正、反用的有效对接中，掌握乘法分配律的结构. 施教时，先让学生独立完成，再选择一道正用和一道反用的等式让学生用乘法的意义解释填写的理由.

2. 横着看，在得数相同的算式后画“？菁”.

本题较上一题有所变化，尤其是第三、第四两组题，第三组题出现了1个74，第四组题得数不相同，从反例让学生感受乘法分配律的结构. 教学时，先让学生独立完成，再让学生用乘法的意义解释 74 × （20 + 1） = 74 × 20 + 74 的理由，40 × 50 + 50 × 90不等于40 × （50 + 90）的理由，从中又让学生分别写出40 × 50 + 50 × 90和40 × （50 + 90）的另一半.

（二）对比练习

算一算，比一比，每组中哪一题的计算比较简便？

第一组：64 × 8 + 36 × 8 （64 + 36） × 8

第二组：25 × 17 + 25 × 3 25 × （17 + 3）

本题练习主要目的是让学生感受运用乘法分配律能使某些计算简便. 施教时，笔者先出示第一组，让学生观察两道算式，猜想它们的结果是否相等. 之后，通过计算、用乘法的意义解释验证. 从而得出64 × 8 + 36 × 8写成（64 + 36） × 8 计算较简便. 独立完成第二组，感受乘法分配律的价值.

（三）解释练习

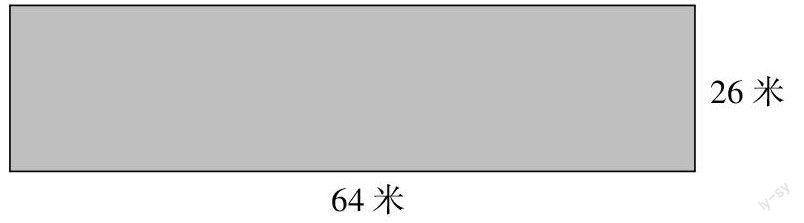
用两种不同的方法计算长方形菜地（如下图）的周长，并说说它们之间的联系.

本题练习主要宗旨是让学生回顾前面已学的长方形周长的计算方法：（长 + 宽） × 2 = 长 × 2 + 宽 × 2，它们之间的联系纽带正是运用了乘法分配律，让学生感受乘法分配律在以往的学习中已经用过，只不过是当时没有明晰罢了.

四、拓展中提升

乘法分配律之所以难，还在于它的多变. 有的要先拆数，如102 × 36要把102拆成100 + 2的和；有的是从两积之和延伸到两积之差，如25 × 176 - 25 × 76；有的还要制造共同乘数，如330 × 42 + 580 × 33，原式中没有共同乘数，但根据等积变形的原理可以将原式变为330 × 42 + 58 × 330或33 × 420 + 580 × 33. 因此，为了盘活学生对乘法分配律的真正运用，笔者进行了拓展练习，在练习中提升学生对乘法分配律本质的认识，培养学生透过现象看本质的能力.

总之，对于乘法分配律的教学，要抓住知识的源头，做好孕伏中的渗透；要以乘法的意义为抓手，运用意义的解释建构新知；要以练习为主线，在练习中达成，拓展中提升.