初中数学教学过程中化归思想的运用

方晓萍

【摘要】 初中数学主要提高学生对数量关系的认识和对空间结构的探索，是联系初级数学和高级数学的纽带. 初中数学教学中辅助教师授课，帮助学生掌握数学知识的主要方法就是教学中化归思想的运用，将晦涩难懂的数学题目变得简单、直观、明了，用简化的思想解决难题，提高解题速度，激发学生思维的灵活性，节省思考时间. 本文从化归思想和数学教学的结合入手，分析初中教学中化归思想的运用.

【关键词】 初中数学教学；化归思想；运用分析

初中数学中的化归思想是数学教学中运用最多、使用最广的解题方法，能够最短时间内将数学教学中繁杂的数量关系、虚无的空间跨越、题目中隐藏公式等问题变得更加单一、直观、已知，易于学生在原有的知识基础上深入理解题目内容，节省解题时间，提高课堂效率，提升教师的教学水平，增强教学的有效性.

1. 化归思想

化归思想是一种具体的思维方式和解题思路，旨在将复杂的事情化简单，将抽象的事物化具体，将事物间隐藏或者模糊的概念和条件转化成学生已知的、熟悉的、可以直观看到的、能够熟练运用的数学公式或定理，然后再依据题目的具体要求，用自己以前学过的一系列知识进行解题.

总的来说，就是将数学知识看作一条连接起来的链条，利用和辩证唯物主义的共通性，用发展变动的眼光看待一切问题，摸清楚数学间的本质联系，用代入法、配方法、待定系数法等解题方法进行代入和转化，将学生不熟悉的题目变成实在的公式，就很容易解决了.

2. 数学教学过程中化归思想的运用

2.1 提高学生的化归意识

首先，培养学生重视化归思想. 教师进行数学教学时，要有意识地对学生进行提醒和重申，先引起学生对化归思想的被动重视，然后逐渐进行渗透教育；或者变化数学问题形式，将几何和代数的问题在两者之间相互转化，将条件众多的复合型题目变成简单易懂的题目，并多次在教学实例中运用化归思想进行解题，增强学生的化归意识.

其次，加强化归思想的应用. 在课堂上，要求学生先用自己的方法解决一道问题，然后教师运用化归思想重新解题，让学生有一个直观的对比，用两者之间的差距让学生明确化归思想的便捷性；在布置作业方面，多布置同类型的作业，增强学生运用化归思想解题的实践次数，让学生无意识地将这种思想方法作为习惯性的解题方法.

2.2 在初中数学教学中运用化归思想

2.2.1 复杂简单化

在数学的学习中，最难的就是复杂的复合型题目，非常让学生头疼. 遇到这种问题，就要学会利用化归思想将题目中无用的句子进行删减，总结出一条清晰明了的问题线，找准关键信息，明确题目要求，然后再进行解答. 如下面的案例：

例1：山羊和绵羊各自驮着货物在主人后边走着，山羊不停地发牢骚，说主人偏心，自己背上的货物太重，快要走不动路了. 绵羊说：“你瞎嘀咕什么呢？我的比你的还要重，我都还没说话呢，如果你给我一袋，我驮的就是你的两倍了，知足吧！”山羊就反驳说：“你再给我一袋，我们就一样多了. ”问：山羊和绵羊各自驮着几袋货物？

当学生一眼看到这道题目时，就会觉得头脑一懵，字数太多，条件理不清，也就无法正确解题了. 反之，摒弃以前的解题方法，用化归思想重新看这道题，将绵羊和山羊背上驮的货物分别设成x和y，根据题目中的条件“如果你给我一袋，我驮的就是你的两倍了”和“你再给我一袋，我们就一样多了”列出具体的方程式：x + 1 = 2（y - 1），y + 1 = x - 1，然后联立方程组，解得x = 7，y = 5. 这样一来，就将题目中的复杂条件转化得很简单，至于计算也就不成问题了. 所以，在遇到比较难的数学问题时，要运用化归思想，将复杂的事物简单化，能够达到事半功倍的效果.

2.2.2 挖掘隐藏的已知条件

有些数学问题，出题者会在题干上有意地隐藏已知条件，并不会出现直观的信息，这就需要学生深挖，仔细阅题，考虑在问题深处的原本已经学过的定理或者公式，将它们运用到本次解题过程中，这也是化归思想的一种运用手段，将隐藏的条件直观化，帮助更快地解答问题.

例2：一个多边形的内角和减去其外角和得到180度，问：这个多边形是几边形？

这个案例考查的是学生对于多边形内角和与外角和的掌握，利于以往知识的回顾：多边形的内角和为（N - 2） × 180，其外角和为360，因此可以得到解答公式：（N - 2） × 180 - 360 = 180，最后解题得解N = 5.

由此可见，用化归思想解题，能够综合题干所给条件和隐藏的信息，作为已知的解题辅助，既能够让学生回顾以往知识结构，补充自身的不足之处，又有助于明确解题思路，加快答题过程.

2.2.3 抽象直观化

化归思想还有一个优势就是能够将抽象的事物变得具体化，将含糊不清或者难以直观表现出来的题目用表格或者其他让学生容易理解、容易接受的方式表现出来，理清思路.

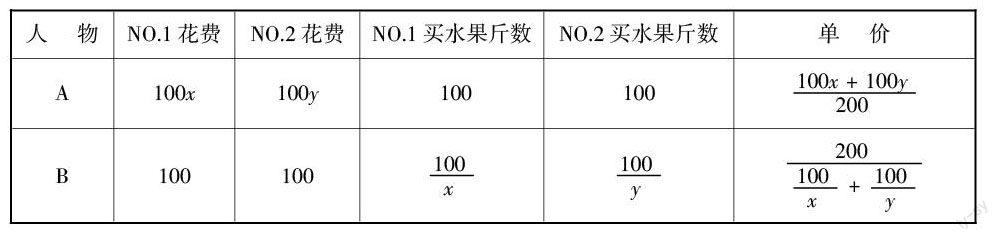
例3：A，B两个人两次在同一家水果店买水果（假设他们两次买的水果单价不同），A每次买100千克的水果，B每次买水果用100元. 如果假设A，B两人第一次买水果的单价为每千克x元，第二次买水果的单价为每千克y元. 若谁两次买水果的平均单价低，谁的购买方式就更合算. 问：A，B两个人谁买水果最合算？

要解这个问题，需要用表格辅助，将题目中抽象的条件真实直观地放在学生面前，根据题目内容，可以得出下图：

化归思想在初中数学教学中的运用，能够将那些让人感到厌烦的数量关系和空间结构用合理的转换样式将题目信息形象、生动、具体地表现出来，根据学生原有的知识结构发散思维，开拓创新；能够顺利理清题目所给的条件和要求，将各种信息连接起来，用变化、发展的眼光看待问题，进而快速高效地解决数学难题.