直讲定义

庄红波

【摘要】本文以高职高专人才培养目标和教育教学改革为背景，结合高等数学在高等医药院校的地位和作用及作者所在学校学生的实际数学基础，谈了对导数定义这堂重要的高等数学教学内容的教学设计和教学过程.主要改变了以前以实例导入为主的教学方法，直讲定义.作为教学探索和交流，有一定的创新和参考价值.

【关键词】高等数学；教学；导数；定义

引 子

高等数学是高等医药院校开设的公共基础课.按现代高职高专教育教学理念，高职高专培养高素质技术、技能实用型人才，应重视学生的专业技能，加强动手能力、实践能力.教学内容上强调“用”，需要基础课给专业课和实训课让路.作为基础课的高等数学当然也必须让路，必须加强自身的改革，让学生有时间和精力学习专业和实训.由此出现矛盾，高等数学内容多，难度大，练习量大，即使以往课时很多，师生也要花很多时间和很大力气教和学.怎样让路？成了棘手的问题.如果简单地删减内容，加快节奏，不仅达不到让路的目的，而且让本来基础就薄弱的学生，得不到良好的高数教育，严重影响今后专业学习，长远来看，不利于学生今后的发展，也不符合高职院校教育教学改革理念.怎样让路？要求我们数学老师在教学上付出更大劳动，更深入钻研教材，更仔细备课，更加直讲精讲，缩短教学时间，提高效率.讲课应节约时间，开门见山；去粗留精，抓住重点；去伪存真，克服难点.总之，化繁为简，更科学、有效地帮助学生更快、更好地掌握高等数学的思想、知识、方法、技能.

教学探索

导数定义是高等数学的入门课，非常重要.教材多以实例方式引入，求运动物体某一时刻的瞬时速率和一元函数某一点的切线斜率.以前，我按教材的这种布局讲：首先提出问题，怎样求瞬时速率和切线斜率；接着引导学生分析解答；最后引入导数概念.那时候，课时多，无可非议，这个讲法很详细，取得了很好的教学效果.但随着教育教学改革的深入，这个方法的不足之处也渐渐暴露.最突出矛盾是课时减少，因为专业课比重加大，基础课比重下降.其次，因为扩招，学生的数学整体水平下降.如果还按以往的教学法讲，课时不够，学生吃力，老师事倍功半.这种背景，要求老师针对高等数学教学存在的矛盾进行分析，提出解决对策；在教学上做一些改革，才能与时俱进，取得好的效果.坚持减少课时为专业课让路的原则，在不缩减内容，不加快节奏的前提下，我在教学上选择了紧扣重点，巧破难点，直讲精讲的教学方法，取得了同样好的教学效果.以导数定义为例我较详细叙述一下直讲定义的处理方式，有什么不妥之处衷心地希望各位专家、前辈、同行批评指正.

一、定 义

考虑到学生已学习极限，上课开始就用极限直接给出导数的定义；函数f（x）在x0处的导数记为f′（x0），定义为f′（x0）=limx→x0f（x）-f（x0）x-x0，引导学生观察、强调变化率比的极限，加深对导数定义的记忆和理解.

二、几何意义

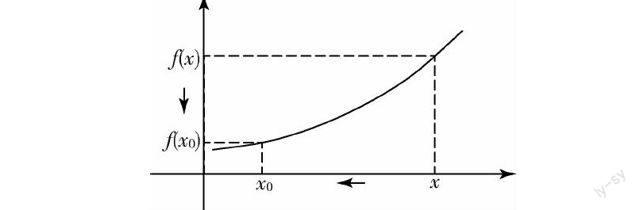
由定义引导学生思考导数的几何意义，同时用投影仪或幻灯展示或用粉笔画出导数的定义示意图，如图所示.

这是很多教材使用的经典示意图，启发学生结合图形和定义思考，自然得出导数f′（x0）的几何意义就是函数f（x）在点（x0，f（x0））处切线的斜率.

三、物理意义

由几何意义进一步提出学生思考导数的物理意义.物理意义更加抽象，更需要老师启发和引导学生结合定义，把x看作时间变量，f（x）看作路程函数进行思考，这样才能得出结论，导数f′（x0）的物理意义是路程函数为f（x）的运动物体在x0时刻的瞬时速率.

四、一些补充

这样讲，开宗明义，教学紧紧围绕导数的定义这个重点，同时把这节课的教学难点，物理意义克服了.剩下的工作是收官，讲解左右导数，导函数，可导，可导与连续的关系，可导与可极限的关系，可导、连续、可极限三者关系等等，这些讲解也可根据课堂气氛和学生掌握情况改为思考和讨论，都是对导数的定义这个教学重点的有益的补充.

五、课后调查

直讲定义，从抽象到一般，同学们排斥还是喜欢？这种方式，讲课直入主题，重点突出，节约时间，张弛有度，有提问，有启发，有讲解，课堂氛围很好；课后，我也做了一些调查，包括提问、讨论、摆谈、问卷等，也得到了大多数学生的喜欢和肯定；最后，我通过课后作业，单元测验，期末考试，纵向比较了现在的处理方式和以前的方法，发现教学效果同样很好.

结语

当然，直讲定义只是一种探索性处理方式，还有很多不同的见解和教法.直入主题，紧扣重点这种教学方法是在响应新时代高职高专教育教学改革号召时，我对所教医药专业学生的高等数学公共基础课所做的初步探索和尝试，为减轻学生基础课压力，多一些时间精力学习专业和实训，以利于今后的发展.再次恳请各位专家、同仁对我的看法提出宝贵意见，谢谢.

【参考文献】

[1]徐晓飒.高职高专教学改革对策探索[J].河南教育学院学报（哲学社会科学版），2011（4）：138-139.

[2]陈映萍，王昌成.面向21世纪高等数学教材改革的实践与认识[J].西南师范大学学报（自然科学版），1999（2）：247-250.

[3]刘良华.高等数学教学存在的问题分析与解决对策[J].咸宁学院学报，2011（7）：139-140.