一次微课教学的尝试

李玉罗

【摘要】 微课是近些年兴起的一种较为新颖的教学方式，将微课结合到数学章节中，以最核心的部分给予展示，体现了微课教学的价值.本文以一次微课探索为尝试，以圆的第一课时为根本进行的，与大家一起交流微课.

【关键词】 微课；圆；初中数学；思维；启发式

近年来，微课愈来愈频繁地被使用于教师课堂教学水平的考核中，各地的各种教师评比都选择使用微课来替代上课，既清晰地展示了教师课堂教学的基本功，也节省了各种评比环节的时间.参阅多种参考资料，笔者发现成功的微课，不外乎下列几个要素：

（1）模式：微课类似于真正的课堂教学，尽管面对评委，但教学时必须做到心中有学生，问答环节自然，这是教师需要注意的首要环节.

（2）设计：微课的设计基本按照正常的课堂教学设计，按照引入、新知、巩固、小结等常用的几个步骤实施，但是在真正表述的环节中具体如何详略得当，还得有区别对待.

（3）表述：表述环节要严格按照正常教学环节，但要注意时间控制，某些表述环节必需详细某些必需简洁，甚至省略，这里的语言需要在微课训练中好好实践.

（4）时间：对于微课初学者而言，时间控制把握、哪些环节宜省略，是往往不易区分的.笔者认为：情境环节的引入、新知的传授是需要详细的，例题和训练的环节是需要简化的，甚至可以一笔带过，小结是需要画龙点睛的，经过合理的安排教师能基本掌握时间的合理控制.

微课案例：“圆”第一课时微课设计

设计1：情境引入（2分钟）

师：同学们，看投影上展示了很多我们生活中的物体，你能说说它们是什么吗？

师：好，大家说出了很多和圆相关的物品，那你能说说形成圆的方式方法吗？（假设学生回答，实际教师自问自答）好，甲同学说用绳子固定一端，然后绕一圈行成了一个圆圈.

设计2：新知探索（6分钟）

师：从上述大家探索圆的形成过程中，我们初步总结出了这样一段话：在一个平面内，线段OA绕着其一端固定的端点O旋转一周，另一个端点所形成的图形叫作圆.固定的端点O叫作圆心，线段OA称之为圆的半径.记作⊙O.下面请同学们分成前后四人一组，分析讨论下面两个问题：

问题（1）：图形上的每个点到圆心有着什么共同的特点？请说明.

问题（2）：这些点到圆心的距离有什么共性？

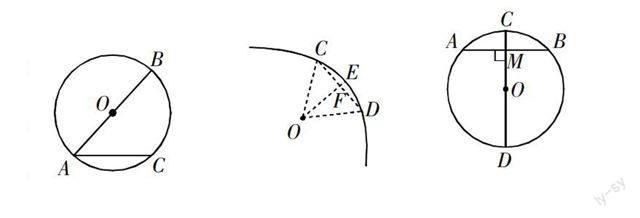
师：好，同学们分析后非常清晰地回答了上述问题.这些长度都等于定长，即半径长，这些点有一个共性，都分布在一个特定的图形上.因此，我们可以将圆的表述简单化、清晰化，抽象出圆更简洁的定义描述：到定点的距离等于定长的点组成的图形，称之为圆.如下图，我们给出一些圆中特定线段的定义：

（1）圆上任意两点的连线段称之为弦，如右图中的弦AC，AB.

（2）经过圆心的弦称之为圆的直径，如直径AB.

（3）圆上任意两点之间的部分，称之为圆弧.其长度大于半圆的，称之为优弧，反之则叫作劣弧.如图中劣弧，优弧.

（4）直径可以把圆分成相等的两部分，两部分相等的圆弧称之为半圆.

组织探索活动1：

（1）圆是轴对称图形吗？请同学们分组探索，并指出圆的对称轴是什么？圆有多少条对称轴呢？

（2）请把你的探索过程画出来，分组交流.

（3）请你通过探索，表述下你的探索过程中如何证明了圆是轴对称图形？

师：很好，同学们的探索非常有新意.看看这一组同学，用折纸对称的方式，证明了圆是一种完美的轴对称图形.另外两组的同学，在一个圆上，画出了很多条直径，向大家展示了圆的对称轴有无数条之多.大家的探索都非常成功.我们可以总结：圆是一种轴对称图形，其对称轴是经过圆心的任意一条直线.

组织探索活动2：

如图，⊙O的直径为CD，作垂直于CD的弦AB，记相交于M.则：（1）该图形是轴对称图形吗？请说明理由.（2）图中哪些等量关系可以得到？请具体说一说.

师：本题正是垂径定理在实际问题中的运用，解决问题过程中需要一定的方程思想，用代数方法解决几何问题，恰是数形结合思想中以数解形的一种体现.解答过程微课环节省略.

设计4：课堂小结（2分钟）

师：同学们，今天的课堂我们学习了哪些知识？对！我们学习了主要三个方面的知识：（1）圆的相关定义.（2）圆是一种轴对称图形，其对称轴是圆的任何一条直径所在的直线.（3）简单地介绍了垂径定理以及运用.

上述是“圆”第一课时的微课尝试.在整个微课向评委展示时，我们可以发现并没有大段的解决问题过程，而是重要介绍了一些引入环节和新知环节，这是本微课的重要环节.通过微课设计，笔者认为微课设计需要合理地阐述教师所设计微课的重点，而不是面面俱到.本微课中，重要环节依旧是新知探索，在其他环节都是教师自问自答模式下进行，尤其在一些活动、例题训练环节等，教师基本是按照正常的解决环节带过，整个微课在12分钟左右.以上是笔者对一次微课的尝试和想法，不足之处恳请大家指正.