悬臂梁限位器非线性动力学效应实验分析*

边菁 徐鉴

（同济大学航空航天与力学学院，上海 200092）

引言

实际工程中很多结构是以梁、板等结构组成.这些结构中为了限制结构件的大幅振动、防止结构破坏，往往会安装一些限位器.例如为提高桥梁的抗震性能并且减小振动幅值而安装的限位器，以及如何适当的安装限位器［1］.另外，机械系统中大量使用的含间隙的零部件都可以使用限位器力学模型，如齿轮啮合间隙、松动的螺丝等.

针对上述类型的工程结构，本文从实验角度出发，研究限位器对悬臂梁结构的动力学效应.近几年，带有限位器的力学结构研究已经成为国内外学术界关注的热点之一.目前已有的文献中，多数含有间隙的结构的理论模型被简化为有限自由度［2-5］，文献［2］将含间隙及集中质量的悬臂梁的动力学模型简化为单自由度和2自由度，并进行了稳定性分析，提出了保持系统稳定性和周期性需要重点考虑的系统参数.文献［3］使用有限元方法建立了梁碰撞的多自由度等效模型并与单自由度模型进行比较，得出单自由度模型大体上能够较好的反应系统的非线性特性.文献［6］使用经验模态分解法得到了系统各阶固有频率下的模态函数，研究结果表明间隙产生的碰撞主要改变了系统的低阶模态，系统的高阶模态可以使用线性的理论.文献［7］使用数值方法研究限位器产生的非线性效应，并对间隙结构的非线性参数进行了辨识.文献［8］使用Hamilton原理建立了受基础激励的刚弹耦合的质量摆模型，表明Hamilton原理适用于含有动位移的边界条件的连续体建模.文献［9］通过实验分析了带限位的悬臂梁系统的非线性特性，并且通过实验研究了接触刚度、间隙以及接触材料对系统的影响，同时使用变分原理提高了该数学模型的数值计算效率.在文献［10］中使用数值方法分析了含间隙悬臂梁系统在不同参数下的分岔情况及可能发生的混沌运动，说明这种非光滑系统存在复杂的非线性动力学行为.文献［11］对悬臂梁单边碰撞做了实验分析并得到了碰撞接触模型，但条件是微碰撞.

综上所述，具有限位器结构的动力学研究已经广泛被学术界和工程界所关注，已有的大部分工作通过理论分析和数值方法进行的，本文的目的主要是通过实验手段，观察带限位的悬臂梁系统非线性动力学特性，重点考察限位器的高度和间隙对悬臂梁系统幅频响应的影响规律以及与多稳态响应之间的关系等，与此同时对实验结果进行时频分析，考察在整个扫频过程中的频率成分，分析可能存在的混沌运动.

本文的第一部分为实验设计介绍，包括实验装置，实验设备以及实验参数.第二部分为实验结果分析，主要研究悬臂梁系统一阶固频附近的幅频响应，多稳态之间的转换过程以及限位器的位置和悬臂梁多稳态区域范围，与限位器接触时的外激励频率的变化关系等.第三部分为时频分析以及谱分析，对扫频过程中所记录的时间历程曲线进行时频分析，考察在整个扫频过程中的频率成分及其能量幅值，以及如何从周期到混沌的实验现象，进一步揭示悬臂梁连续体模型与间隙系统两者结合产生的强非线性效应.

1 实验装置

首先，制作具有限位器的悬臂梁振动系统，如图1a和1b所示，整个实验装置固定在电动振动台的台面上（图1a），垂直悬臂梁一端固定在一个铝合金平板上，用双排螺丝将其夹紧；另一端连接加速度传感器.为使系统平衡，梁两侧都固定有加速度传感器，并将其视作附加质量.固定在铝合金板上的限位器的高度和宽度可调，实验装置的细节图如图1b所示，其中：1.电动振动台系统，包括振动控制系统、功率放大器、振动台体和热交换器；2.加速度传感器采集系统，包括加速度传感器、信号采集与分析仪和PC机；3.可调高度位置限位器和间隙宽度的限位器；4.不锈钢悬臂梁.

图1 实验装置：（a）实验装置总体布置图；（b）实验装置细节图Fig.1 Experimental device：（a）overview of experimental device；（b）details of experimental device

实验装置的参数如表1所示：

表1 实验参数符号的定义和取值Table 1 Symbols and values of the experimental parameters

系统的振动驱动由振动台提供，该激振动台的有效起振频率为5Hz.在低于5Hz时，振动台的振幅不稳定.外激励幅值可由控制系统进行调节，外激励频率可由振动控制仪进行设置和调节.振动台体上固定有加速度传感器，所以基础激励可以及时测得并进行控制.所测得实验数据由信号采集与分析仪记录、处理.电动振动台的工作流程如图2所示，

图2 振动台的工作流程图Fig.2 Scheme of vibration experiment

实验是通过振动控制仪使基础的加速度值控制在0.1g.扫频范围为5-11Hz左右（悬臂梁一阶固有频率附近）.扫频速率：0.2Hz/min.

2 实验结果

2.1 未加限位器时的幅频响应

首先，在未加限位器时，系统的幅频响应曲线表现出典型的线性动态系统的特征，如图3所示，其中横坐标为外激励频率/Hz，纵坐标为悬臂梁自由端加速度幅值/（m/s2）.实验中使用锤击法测得悬臂梁的一阶频率为6.24Hz，二阶固频为47.094Hz，三阶固频为140.88Hz.后面的实验重点是系统在悬臂梁第一阶频率附近的动力学响应，如图3所示：

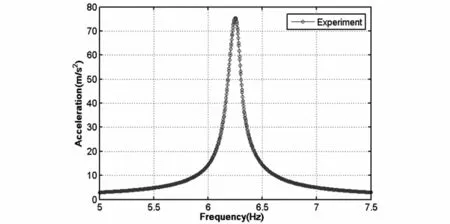
图3 未加限位器的悬臂梁幅频响应图Fig.3 Amplitude-frequency response of cantilever beam without stoppers

2.2 带有限位器悬臂梁幅频响应

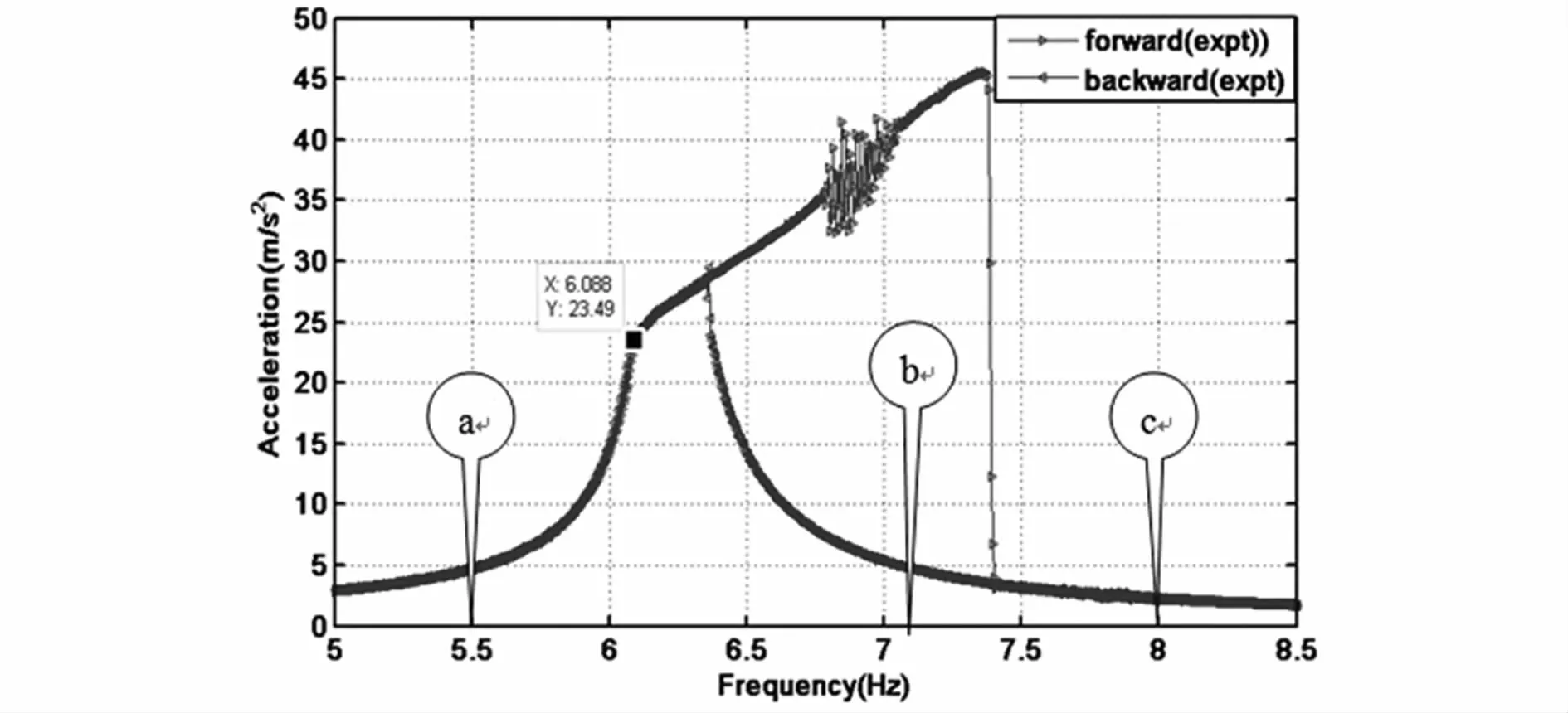
图4 带限位器的悬臂梁幅频曲线图（s＝0.1g，Δ＝5mm，L1＝125mm）Fig.4 Amplitude-frequency response of cantilever beam with stoppers（s＝0.1g，Δ＝5mm，L1＝125mm）

首先，固定限位器的位置.限位器到梁固定端距离，即：L1＝125mm，Δ＝5mm，振动台驱动外激励加速度s＝0.1g，通过正向和反向扫频得到幅频曲线如图4所示.其中纵坐标是悬臂梁自由端加速度响应，横坐标是外激励驱动频率，范围在5Hz-8.5Hz.从图4可看出，随着在外激励频率从5Hz开始增加，悬臂梁自由端的加速度响应沿着图4的上半支连续增大，直到外激励频率为6.088Hz时，加速度响应曲线出现拐点而改变方向，加速度增长速率开始变缓，这时悬臂梁与限位器接触.进一步增大外激励频率直到7.4Hz时，加速度响应突然跳跃到一个小的幅值，说明悬臂梁由一个大振幅运动跳跃到小振幅的周期运动.而反向扫频或者随着外激励频率从8.5HZ持续减小时，加速度响应沿着图中曲线的下半支缓慢增加，直到6.4Hz时，加速度响应突然跳跃到较大的振幅，这个增长的过程并不连续，是一种跳跃的过程.进一步减少外激励频率，加速度响应幅值开始减小，直到6.4Hz时曲线出现拐点后继续减小.于是，当外激励频率在6.4Hz到7.4Hz范围内，加速度响应伴随着跳跃出现两个稳态响应，这是是非线性振动系统特有的现象之一，说明本文构建的实验系统是非线性动力学系统.

为了考察图4中表示的不同频率下悬臂梁的振动特性，分别取外激励频率标记在图4中a，b和c处的三个频率值：5.5Hz，7.2Hz和8Hz，做定频激励以考察悬臂梁自由端处的时间历程响应，等系统运动稳定后开始记录数据，如图5a，5b和5c所示.

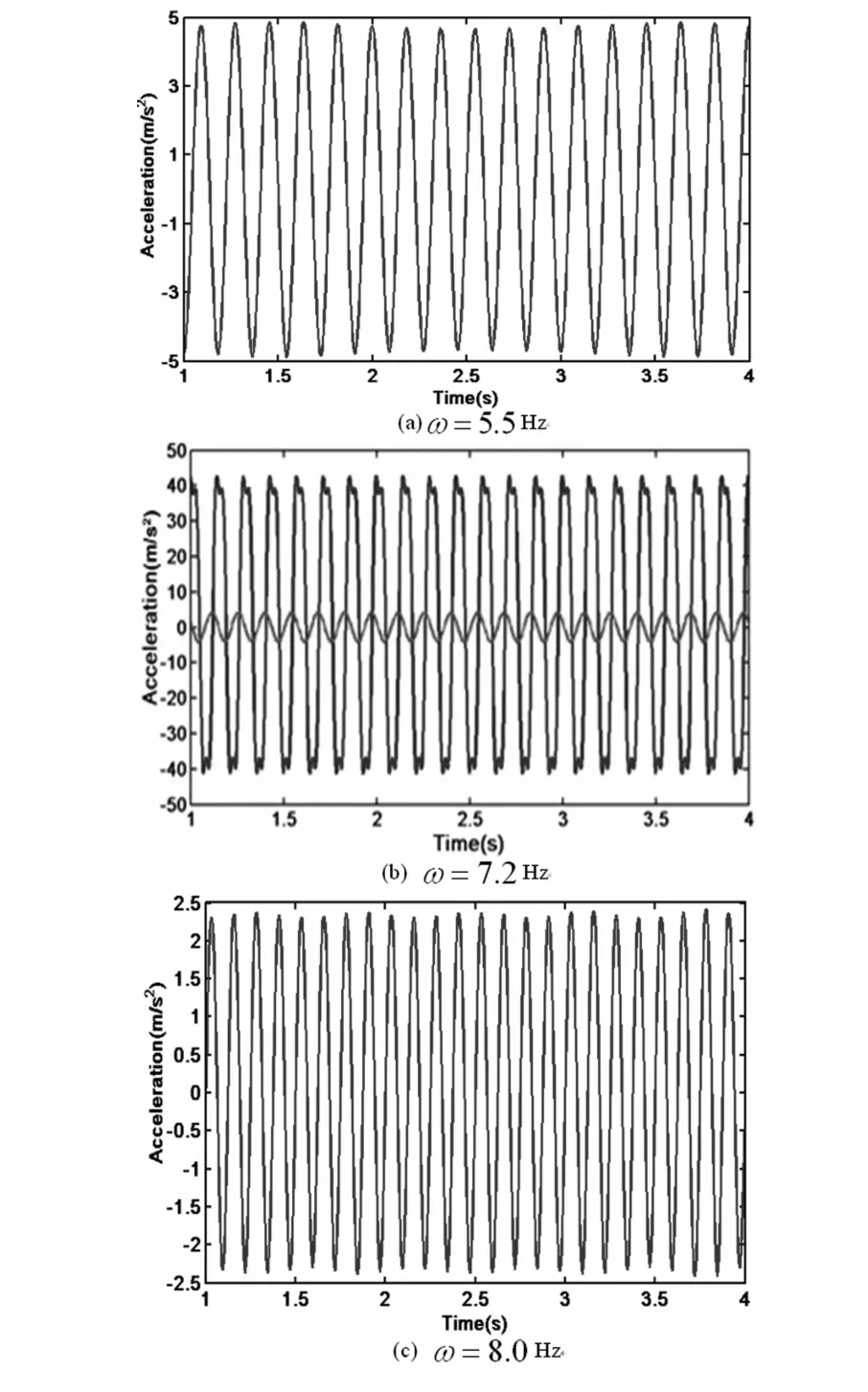
图5 不同外激励频率下悬臂梁的时间历程图Fig.5 Time histories of the cantilever system versus excitation frequencies

图5表明对应不同的外激励频率，悬臂梁的响应可以表现为单稳态（图5a和5c）和双稳态运动（图5b）的实验结果.双稳态的出现，即大振幅运动和小振幅运动依赖于悬臂梁的初始状态的改变.因此，在悬臂梁振动过程中，对悬臂梁进行扰动，可以改变悬臂梁的振动幅值，可以从大振幅变成小振幅，也可以从小振幅变成大振幅的状态.为了进一步验证这样的结论，取外激励频率分别是6.5Hz和7.3Hz，再一次考察悬臂梁的时间历程，正如图6和7所示.图6a表明初始静止状态的悬臂梁受到外激励频率6.5Hz的驱动，首先进入小振幅周期振动，运动进入稳态后在某一时候加以一个冲击扰动后，经过一段时间稳定后，振动幅值变大，对应于图4中从下半支跳到上半支.图6b表明了相反的过程.外激励频率为7.3HZ时类似的实验结果表明在图7中.图4-7表明了典型的非线性振动特征，实验结果意味着适当的扰动可以抑制振动幅值，对工程应用中的减振控制有重要的参考价值.

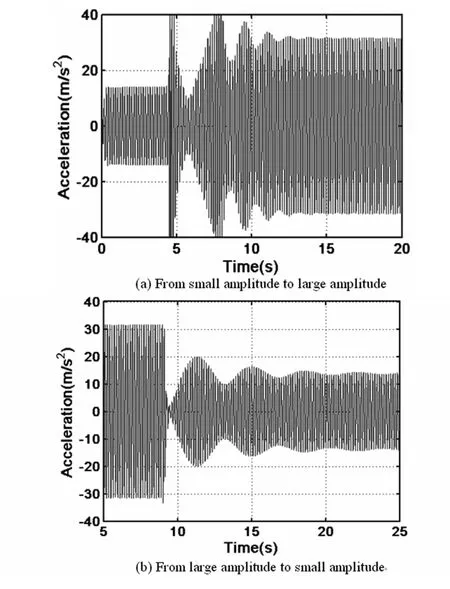
图6 悬臂梁的双稳态（ω＝6.5Hz）Fig.6 Time histories of the cantilever system（ω＝6.5Hz）

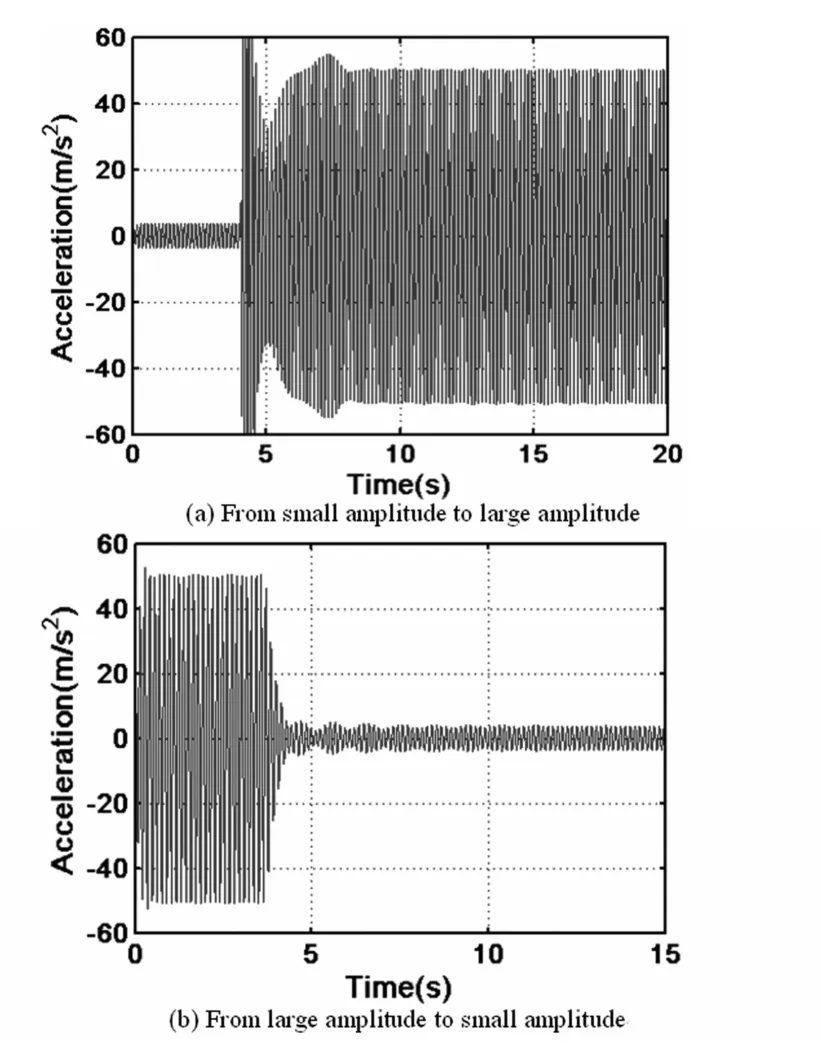
图7 悬臂梁的时程图（ω＝7.3Hz）Fig.7 Time histories of the cantilever system（ω＝7.3Hz）

2.3 限位器的高度L1对系统动力学行为的影响

情形1固定限位器宽度Δ＝2.5mm

这部分主要的研究内容是固定Δ，在不同L1时，比较悬臂梁的幅频曲线，包括悬臂梁与限位器接触时的参数取值，多稳态区域范围以及跳跃点位置.首先固定限位器宽度Δ＝2.5mm，外激励加速度为0.1g时，然后调节限位器高度L1.将加速度转化为位移得到图8：

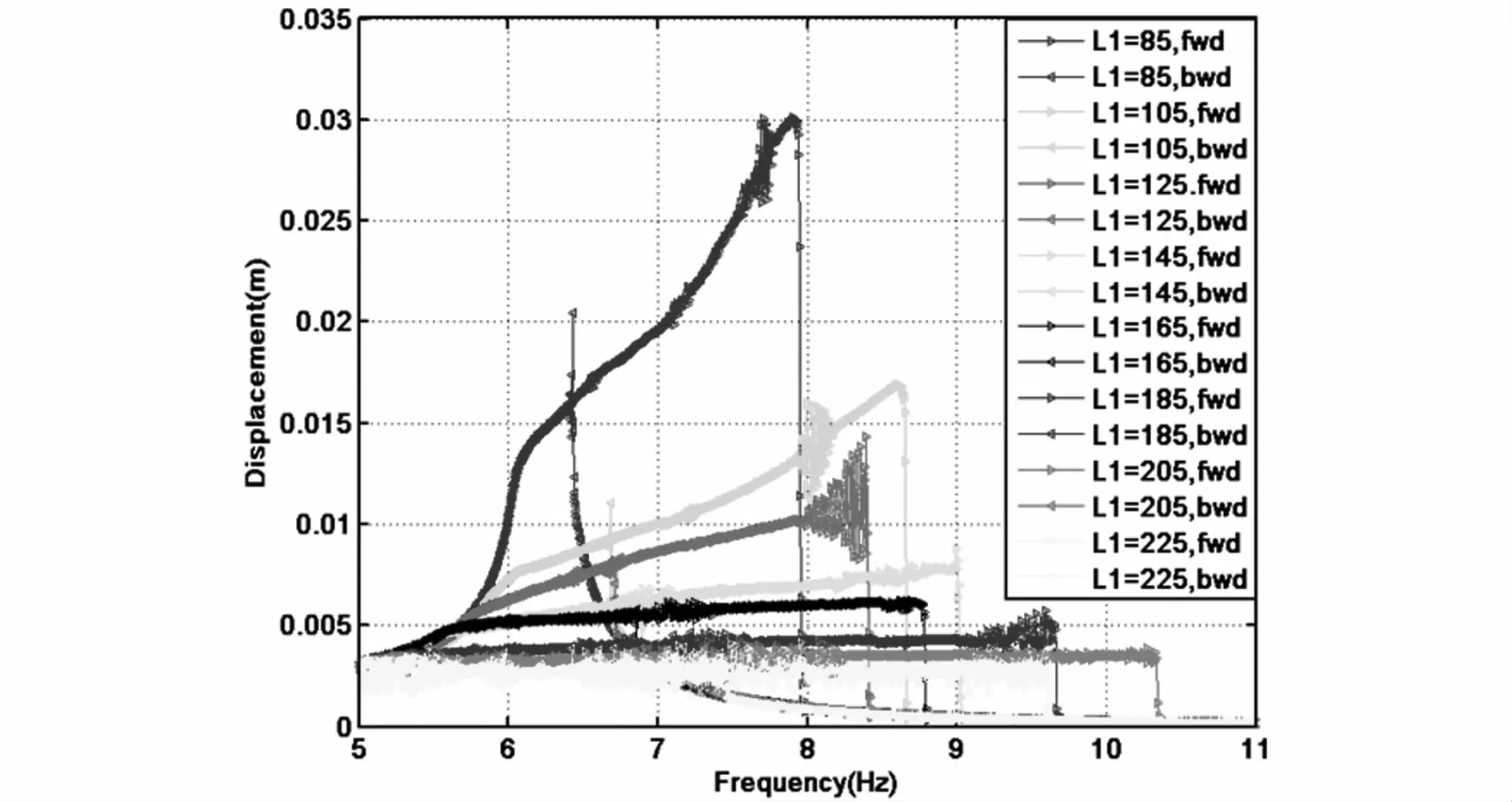
图8 悬臂梁的一组幅频响应曲线（Δ＝2.5mm）Fig.8 A series of amplitude-frequency response curves（Δ＝2.5mm）

图8为Δ＝2.5mm时，取不同L1得到的悬臂梁在其线性一阶固频附近正扫和反扫的幅频响应曲线的实验数据图.横坐标为外激励频率/Hz，纵坐标为悬臂梁自由端端点的位移幅值/m.图8中的不同颜色的曲线代表不同的L1的取值，由高到低L1依次增大.同时，同一种颜色分为正扫和反扫两种扫频方式.由图8可以明显的看出，随着L1的逐渐增大，悬臂梁的振动幅值受到限位器的限制而逐渐减小.除个别曲线外（绿色、黑色、黄色），跳跃点的位置也随之向后移动；同时，多稳态的区间范围也逐渐增大.同时可以看出，当限位器放置在较低的位置时，如图8中的黄色曲线（L1＝225mm），悬臂梁此时已不是周期运动，其运动情况十分复杂，幅值差别较大.为进一步的分析多稳态区域范围与L1之间的关系以及外激励频率与L1之间的关系，将Δ分别取3/4mm时，然后进一步的对这些规律进行分析.

情形2固定限位器宽度Δ＝3mm

将 Δ固定为3mm，s为0.1g，然后调节L1，得到悬臂梁的幅频曲线如图9.

图9中的不同颜色的曲线代表不同的L1的取值.由图9同样可以看出，随着L1的逐渐增大，悬臂梁的振动幅值受到限位器的限制而逐渐减小.除去绿色和黄色曲线，跳跃点的位置都随L1的增大而向后移动，多稳态的区间范围也逐渐增大.同时可以看出，和图7一样，当限位器放置在较低的位置时，如黄色曲线（L1＝225mm），悬臂梁的运动变得复杂.

图9 悬臂梁的一组幅频响应曲线（Δ＝3mm）Fig.9 A series of amplitude-frequency response curves（Δ＝3mm）

情形3固定限位器宽度Δ＝4mm

将 Δ固定为4mm，s为0.1g，然后调节L1，得到的悬臂梁的幅频曲线图10.

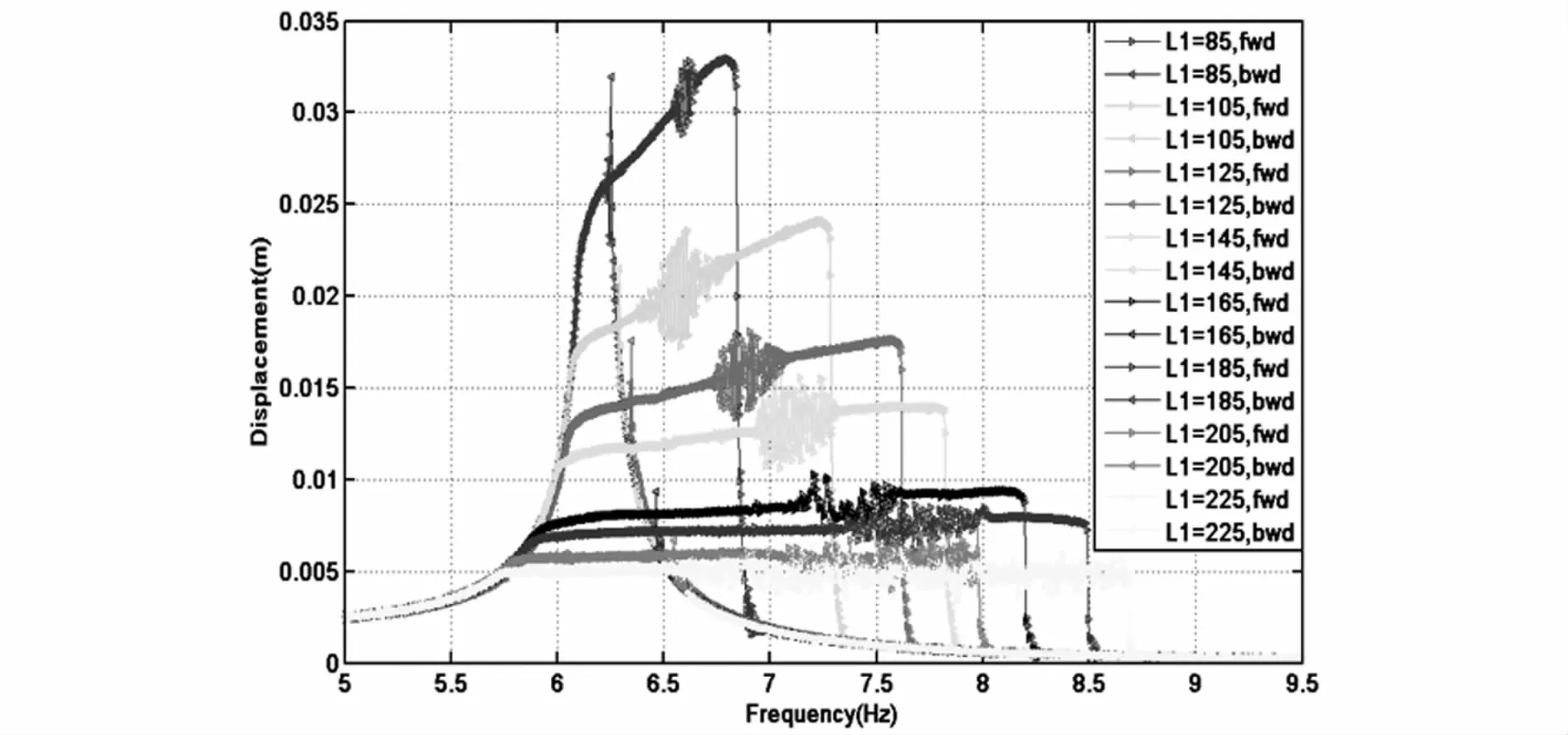
图10 悬臂梁的一组幅频响应曲线（Δ＝4mm）Fig.10 A series of amplitude-frequency response curves（Δ＝4mm）

同样的，图10中的不同颜色的曲线代表不同的L1的取值，曲线由高到低表示L1的取值依次增大.可以看出随着L1的逐渐增大，悬臂梁的振动幅值受到限位器的限制而逐渐减小.除去粉色曲线，跳跃点的位置都随L1的增大而向后移动，多稳态的区间范围也逐渐增大，此时的关系变化较为明显.同样可以看出，当限位器放置在较低的位置时，如黄色曲线（L1＝225mm），悬臂梁的运动变得复杂，已不是周期运动.

为进一步分析悬臂梁与限位器接触时外激励的频率和L1的变化关系，以及悬臂梁幅频曲线中多稳态的范围与L1的关系，将图8、9、10中的每条曲线的幅值的转折点取出，每个点对应一个外激励频率.将相同的Δ下的外激励频率值绘制成一条曲线，得到外激励频率与L1的关系如图11.

图11 ω与L1的关系（Δ＝2.5/3/4mm）Fig.11 Relationships betweenωand L1（Δ＝2.5/3/4mm）

图11为Δ分别为2.5/3/4mm时，调节L1时，悬臂梁与限位器接触时外激励频率的取值.纵坐标为L1的取值/m；横坐标为悬臂梁与限位器接触时对应的外激励的频率/Hz.由图11可以看出，Δ固定时（2.5mm），L1的取值越小，即限位器放置在离悬臂梁固定端较近的位置时，悬臂梁与限位器接触时的外激励频率越高.意味着限位器放置的越高，需要外激励频率接近其一阶固频6.25Hz时，悬臂梁才会与限位器接触.这种结论在不同的Δ时，同样成立.取Δ＝3/4mm时，曲线的变化情况大致相同：如图11中绿色和红色曲线所示.

图11中的蓝色曲线的Δ＝2.5mm，是由离散的实验数据绘制成的曲线.对其进一步的分析，得到图12中的响应的拟合曲线以及对应的方程，图中横坐标为L1/mm的取值，纵坐标为外激励频率/Hz.如图12：

图12 ω与L1的关系（Δ＝2.5mm）Fig.12 Relationships betweenωand L1（Δ＝2.5mm）

图12中红色曲线为拟合出的ω与L1之间的含三次项的曲线关系.蓝色点为实验数据，每个点表示在某个L1时，悬臂梁刚好与限位器接触时的外激励频率，即幅频曲线中的幅值的转折点的横坐标取值.通过比较红色和蓝色曲线可知，该拟合曲线已足够达到需要的精度.方程中的y为外激励频率，x为限位器高度.此方程可作为悬臂梁与限位器接触条件的判据.在进行理论计算时，可带入上图中点的位移幅值作为刚度分段的依据.

从图8、9、10中得到的L1与幅频曲线中多稳态区域范围的关系如图13所示.图13中横坐标为L1的取值，纵坐标为对应的不同的L1条件下，多稳态区域的范围（the frequency range of multi-stable state），简写做FRMS/Hz.图中，三条曲线表示三种不同的Δ取值.

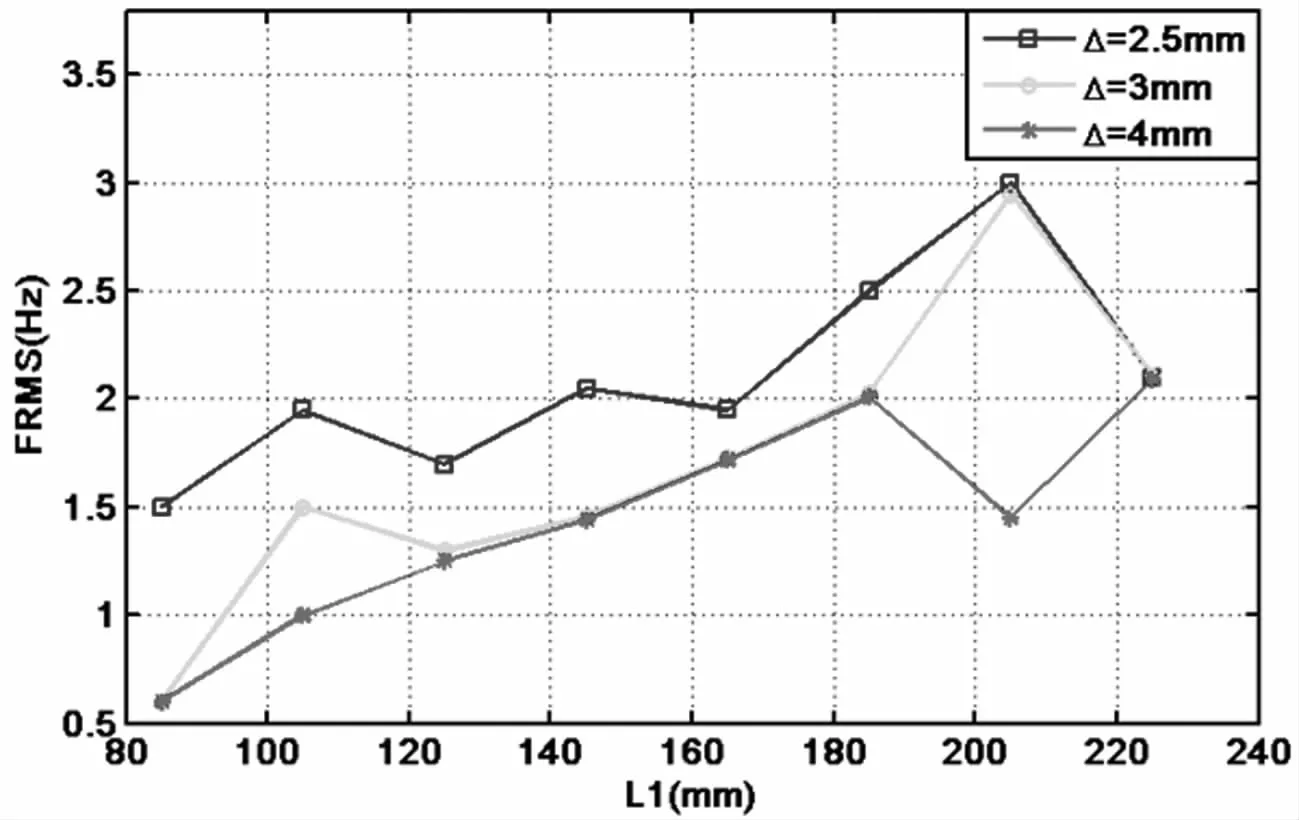
图13 多稳态区域与L1之间的关系Fig.13 Relationships between FRMS and L1

图13可以看出，在L1小于115mm时，FRMS与L1成正比，在接近梁的中间位置（125-165mm）时，蓝色曲线（Δ＝2.5mm）中，FRMS随L1的变化并没有统一的规律，尤其是在125-165mm范围内比较复杂.红色曲线中的两个点（L1＝105mm、205mm）与其余两条曲线不同，比较特殊.其余的两条曲线的变化规律比较相似，总体上将，都是随L1的增加，FRMS成上升趋势.特别的，当L1＝205mm时，蓝色与绿色曲线达到其最大值，但红色曲线却突然下降.另外，在限位器放置在225mm时，FRMS都回到一个固定的值2.1Hz.

总体上，实验结果的得到FRMS的值与L1的关系比较复杂，没有统一的关系.可见，在实验中得到的结果比预期的复杂.

2.4 限位器的宽度Δ对系统动力学行为的影响

这部分主要的研究内容为调节不同限位器宽度Δ，研究方法与上节内容相同，即比较一组悬臂梁的幅频曲线中所展示的非线性现象.包括悬臂梁与限位器接触时的参数取值，多稳态区域范围以及跳跃点位置.在这个过程中，每一组幅频曲线的L1固定，Δ变化，一共得到三组幅频曲线.具体实验参数取值为：L1＝85mm，s＝0.1g，调节限位器宽度 Δ.得到图14.同理，L1分别取95/105mm时，得到图15和图16.图中横坐标为外激励频率/Hz，纵坐标为悬臂梁自由端的位移幅值.

图14 悬臂梁的幅频响应图（L1＝85mm，Δ＝2/3/4/5mm）Fig.14 Amplitude-frequency response curves（L1＝85mm，Δ＝2/3/4/5mm）

图15 悬臂梁的幅频响应图（L1＝95mm，Δ＝2/3/4/5mm）Fig.15 Amplitude-frequency response curves（L1＝95mm，Δ＝2/3/4/5mm）

图16 悬臂梁的幅频响应图（L1＝105mm，Δ＝2/3/4/5mm）Fig.16 Amplitude-frequency response curves（L1＝105mm，Δ＝2/3/4/5mm）

从图14、15、16可以看出，Δ越小，悬臂梁的振动幅值会相应的受到限制进一步减小；悬臂梁与限位器接触时的ω也随Δ的增大而增大，逐渐向一阶固频6.25Hz靠近.同时对三张图进行比较可以看出，图中幅频曲线中对应的多稳态的范围也和Δ有着明显的变化关系，除了图15中的黑色曲线，其余各图中的每条曲线的多稳态范围都是随着Δ的减小而增大.

为了进一步分析悬臂梁与限位器接触时ω取值情况，将以上三张幅频曲线图中悬臂梁与限位器恰好接触时的点取出，得到三簇不同的Δ时，悬臂梁与限位器接触时的ω取值.目的是要考察在固定L1的情况下，Δ与ω之间的变化关系，如图17所示，图中横坐标为Δ/mm；纵坐标为悬臂梁恰好与限位器接触时的ω/Hz.图17中的三条曲线表示L1分别为85/95/105mm时，接触点的外激励频率与Δ之间的关系.

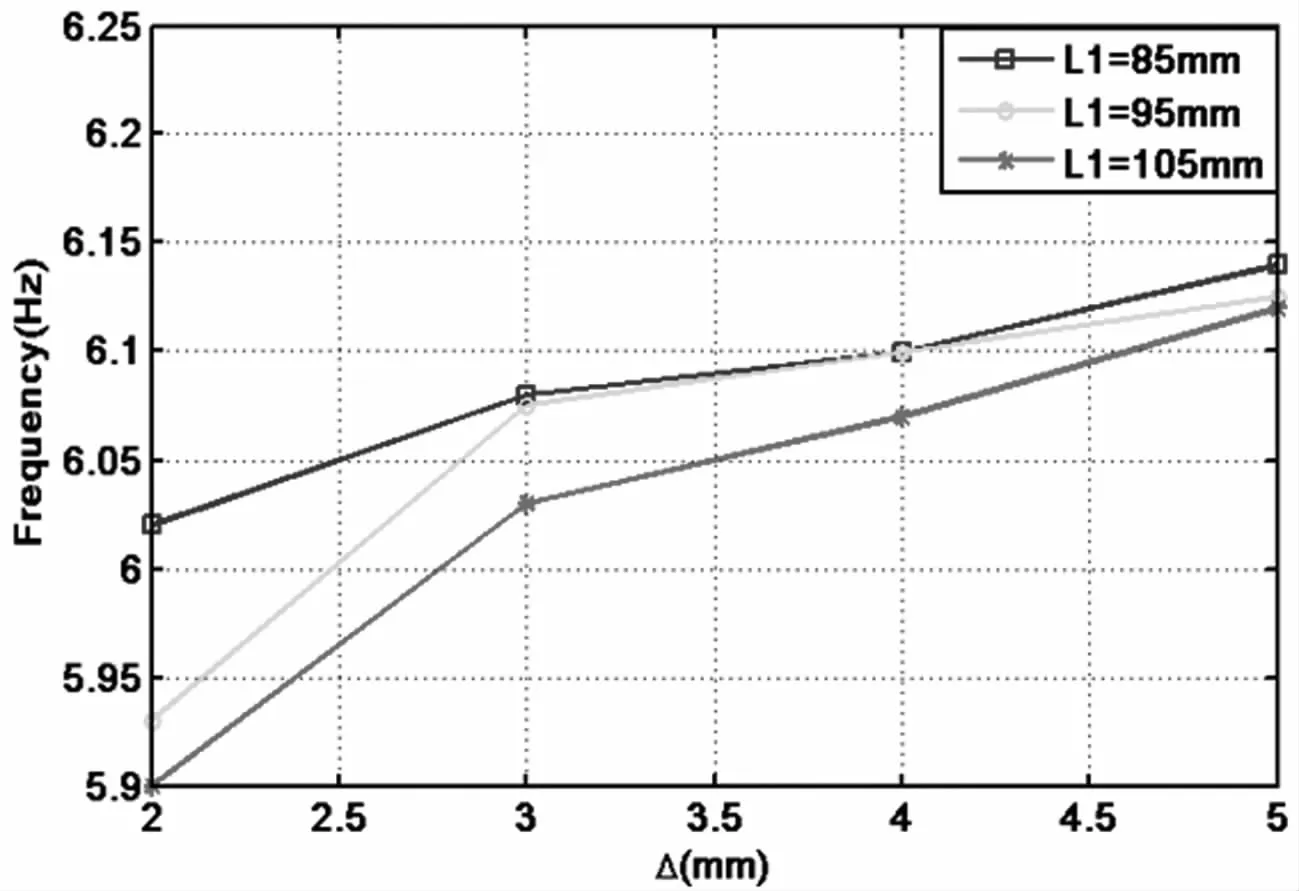
图17 ω与Δ之间的关系Fig.17 Relationships betweenωandΔ

由图17中的蓝色曲线的变化趋势可知：当L1固定时（85mm），Δ越大，悬臂梁与限位器接触时的外激励频率越高，即限位器越宽，需要外激励频率接近其一阶固频6.25Hz时，悬臂梁才会与限位器接触.取时L1＝95/105mm时，曲线的变化情况大致相同，总体上成上升趋势.说明这种变化趋势在不同的L1时，同样成立.

进一步考察本节实验结果中，多稳态区域的范围大小与Δ之间的变化关系.从图14、15、16中可以得到每个幅频曲线中的多稳态的范围宽度（FRMS），将相同的L1中的实验数据绘制成一条曲线，一共可以得到三条曲线.进行总结，得到图18：

图18 多稳态区域与Δ之间的关系Fig.18 Relationships between FRMSandΔ

图18为Δ与FRMS之间的关系.横坐标为可调参数Δ的取值/mm，纵坐标为对应的FRMS/Hz.由图18可以知，除去图中的绿色曲线中的一个点（Δ＝5mm），FRMS与 Δ有明显的关系，即随着Δ的增大，FRMS逐渐减小.在不同的L1（85/105mm）时，这种变化关系都成立.

2.5 限位器对悬臂梁动力学行为影响的分析

分别调节L1与Δ，得到了不同情况下的带限位的悬臂梁的幅频曲线图，并得到一些L1和Δ对这种悬臂梁动力学行为影响的规律，主要有以下几个方面：

限位器能很好的限制悬臂梁振动幅值，限位器放置的位置越低宽度越窄，悬臂梁的振动幅值越小.但限位器会带来一些非线性的动力学行为，如多稳态、跳跃等.增加了对该系统进行控制、减振的难度，但也可利用这些非线性现象进行减振控制.

限位器的高度L1与多稳态区域范围的大小关系复杂，总体来讲随着L1的增大，多稳态的区域变宽，但在L1接近自由端端点时，多稳态的区域范围回到一个固定的值.另外，L1越大，悬臂梁与限位器接触时的外激励频率越小.

限位器的宽度Δ与系统多稳态范围的关系十分明显.总的来讲，Δ越小，多稳态的范围越大.另外，Δ增大时，悬臂梁与限位器接触时的外激励频率越大，接近悬臂梁的一阶固频6.25Hz.

3 时频分析

取L1＝125mm，Δ＝2.5mm，s＝0.1g，得到悬臂梁的幅频曲线如图19.由于本节的考察内容主要外激励频率从小到大变化时，悬臂梁与限位器接触后的复杂动力学行为，所以只需分析正扫过程.如图19所示，为悬臂梁的振动幅值随外激励增大时的变化曲线.横坐标为外激励频率/Hz，纵坐标为悬臂梁自由端加速度幅值/（m/s2）.由图可知，在6.7Hz与8Hz附近，悬臂梁并非做周期运动，而是呈现出复杂的动力学行为.为了进一步的分析，在扫频过程中使用信号采集仪记录整个扫频过程中悬臂梁自由端的时间历程，并进行时频分析，即分析整个随外激励频率变化的时间历程图的频率成分及其能量幅值，得到图20.

图20中的横坐标表示的是外激励频率/Hz由大到小变化的过程；纵坐标为对悬臂梁自由端响应的时间历程进行时频分析后响应中包含的全部频率成分/Hz.颜色的亮度代表该频率下的能量幅值的大小，红色部分表示幅值最大，蓝色部分表示幅值接近零.由图20可知，在外激励频率小于6Hz时，悬臂梁并未与限位器接触，所以响应中只含有外激励的频率，几乎没有其它的频率成分，这时系统是典型的线性系统.当外激励频率从6Hz开始逐渐增大时，响应中开始包含其它的频率成分，如三倍频，五倍频等，表现为在图20中，横坐标从6Hz开始从一条线分为很多条线，表示此时响应中含有不同的倍频成分，且吸收了部分的能量，已不能忽略.值得注意的是在6.75Hz附近的频率成分十分复杂，已不是离散的线，同时在7.8Hz-8.1Hz的变化过程中可明显的看出响应的频率成分已从离散变为连续，同时分布在整个频率段上（0-150Hz）.

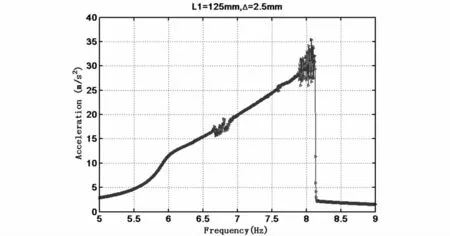
图19 幅频响应曲线图（L1＝125mm，Δ＝2.5mm，s＝0.1g，正扫）Fig.19 Amplitude-frequency response curve（L1＝125mm，Δ＝2.5mm，s＝0.1g，forward）

图20 时频分析Fig.20 Time-frequency analysis

图21 随外激励频率变化的时间历程图Fig.21 Time histories with excitation frequency variation

图21表示的是外激励频率从7.7Hz到8Hz时，悬臂梁自由端处的时间历程图，横坐标为外激励

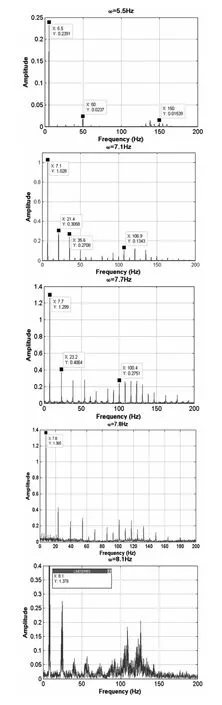
图22 频谱分析Fig.22 Spectrum analysis

频率的变化过程/Hz，纵坐标为悬臂梁自由端加速度值/（m/s2）.由于该时程图是在匀速扫频（0.2Hz/min）过程中记录下来的，所以为方便和图19，20做比较，纵坐标采用外激励频率的变化代替时间的变化.从图中可以看出，在7.7Hz到7.8Hz的扫频过程中，悬臂梁的响应为概周期，可以看出明显的包络线.从7.8Hz开始，系统的响应开始变的复杂，有混沌运动的趋势.为确定这种变化过程是否为概周期通往混沌的途径，进一步做频谱分析，得到不同外激励频率下的悬臂梁响应的频谱图，如图22（ae）所示.图22中的频谱图分别与图19，20中的频率点对应.

在图19中选取不同的外激励频率下的点，分进行频谱分析得到图22a-e.对应为a：悬臂梁未与限位器接触做周期运动，频谱图上只有一个主要的频率（5.5Hz），50Hz是振动台的一阶固频.b：此时悬臂梁与限位器接触，从频谱图上可以看出，系统做周期运动，但同时含有三倍频、五倍频等倍频成分.c：频谱图中倍频集中了大量的能量，但是开始有不可约的频率成分进入，在图19中表现为时间历程图中有明显的包络线，为概周期运动；d：从7.8Hz开始，频率成分开始从离散变为连续，逐渐进入混动运动；e：频谱图上出现连续普，各种频率成分都进入到运动中，说明系统此时的状态为混沌运动.

图22a-e展示了带限位悬臂梁系统从周期到混沌运动的一系列变化过程.说明本文中的分段非光滑系统可以在一定的条件下（限位器位置），产生复杂的混沌运动.该过程是一个周期到混沌再到跳跃的特殊的非线性现象，有重要的实验和理论价值.

4 结论

本文设计了一个带限位悬臂梁非光滑系统的实验装置，通过大量的实验考察了不同的限位器高度和宽度对悬臂梁的动力学行为的影响.得出以下结论：

（1）悬臂梁与限位器接触时会产生多稳态的情况，根据初始条件的不同，在特定频率区域内，该悬臂梁系统会产生多稳态以及跳跃的非线性现象.

（2）多稳态区域大小取决于限位器宽度和高度的共同作用，同时得到限位器高度、宽度与多稳态区域大小的变化关系.

（3）得到在不同的限位器高度和宽度下，悬臂梁与限位器接触时的频率的临界值，这些曲线可以作为判断悬臂梁与限位器接触的判据.

（4）在扫频过程中记录了相应的时程曲线并进行了时频分析，得到了随外激励频率变化下系统响应的频率分成的变化趋势，并得到了由周期运动到混沌再到跳跃的实验现象.

文章所得到的实验结果说明这种非光滑系统存在丰富的强非线性现象，得到的结论对带有限位或间隙的连续体系统有实际的工程指导意义，可为带限位的悬臂梁系统的减振控制提供实验依据.

1 许祥，刘伟庆，徐秀丽等.考虑限位器影响的山区连续桥梁地震响应分析.南京工业大学学报，2012，34（7）：1～7（Xu X，Liu W Q，Xu X L，et al.Earthquake response analysis of continuous girder bridges in mountain area considering effect of restrainers.Journal of Nanjing University of Technology（Natural Science Edition），2012，34（7）：1～7（in Chinese））

2 Blazejczyk B，Czolczynski，K，Kapitaniak T.Dynamics of a two-degree-of-freedom cantilever beam with impacts.Chaos Solitons Fractals，2009，40：1991～2006

3 Andreaus U，Placidi L，Rega G.Soft impact dynamics of a cantilever beam：equivalent SDOFmodel versus infinite-dimensional system.Journal of Mechanical Engineering Science，2011，225：2444～2456

4 Megahed SM，Haroun A F.Analysis of the dynamic behavioral performance of mechanical systems with multi-clearance joints.Journal of Computational and Nonlinear Dynamics，2011，7（1）：011002

5 Luo GW，Lv X H，Zhu X F.Dynamics of vib-impactmechanical systems with large dissipation.International Journal of Mechanical Science，2008，50：214～232

6 Mehmet K，Heng C，Young SL.Nonlinear system identification of the dynamics of a vibro-impact beam：numerical results.Archive of Applied Mechanics，2012，82：1461～1479

7 Marchesiello S，Garibaldi L.Identification of clearancetype nonlinearities.Mechanical Systems and Signal Processing，2008，22：1133-1145

8 陈娟娟，徐鉴.刚弹耦合质量摆减振结构的动力学建模.动力学与控制学报，2009，07（4）：363～365（Chen J J，Xu J.The dynamic modeling for the damping structure with amass pendulum considering the rigid elastic coupling effects.Journal of Dynamics and Control，2009，07（4）：363～365（in Chinese））

9 Krishna IR，Padmanabhan C.Experimentaland numerical investigations of impacting cantilever beams part 1：firstmode response.Nonlinear Dynamics，2012，67：1985～2000

10 Wang L，Ni Q，Huang Y.Bifurcation and chaos in a forced cantilever system with impacts.Journal of Sound and Vibration，2006，296：1068～1078

11 Hassan J，Hamid A，Fatemeh P.Identification ofmicrovibro-impacts at boundary condition of a nonlinear beam.Mechanical Systems and Signal Processing，2010，25：1073～1085