冷质部件支撑结构中压杆的动力稳定性分析*

谭宁 卢勃勃 陈玲莉 吴莹

（西安交通大学航天航空学院机械结构强度与振动国家重点实验室，西安 710049）

引言

先进超导托卡马克实验装置（Experimental Advanced Superconducting Tokamak，简称EAST）是国家“九五”重大科学工程项目.EAST主机装置主要由超导极向场磁体、超导纵场磁体、真空室、内外冷屏、外真空杜瓦及支撑结构等几大部件组成.冷质量支撑系统是超导耦合磁体系统中的关键部件，要能够承受磁体在各种状况下施加在耦合磁体上的轴向作用力、磁体自身重力和冷却过程中的热应力［1-6］.我国科学家针对我国的托克马克装置EAST的支撑结构设计了两种支撑方案，圆杆式柔性结构支撑和板式柔性结构支撑［3-6］.支撑系统除了在静载荷条件下要有足够的强度、刚度、稳定性外，还要解决运行时的热负荷、电磁力以及热胀冷缩引起的热应力所带来的影响.超导托卡马克实验装置在稳态运行时的特点是纵场系统处于液氦的低温状态，支撑系统是连接纵场系统和基座的桥梁，这就导致支撑系统在工作过程中一端处于低温，而另一端处于室温，使整个支撑由下向上存在着一个温度梯度.而且，整个装置从开始到稳定工作的过程中，纵场系统从室温到低温不断变化.

结构的动力稳定性问题长期以来一直受到人们的广泛重视，由于时间参数的引入，使得问题变得复杂.在周期性载荷作用下，当压杆的自振频率与外载荷的强迫振动频率非常接近时，压杆将产生强烈的共振现象.前苏联学者B.B.鲍洛金在其著作《弹性体系的动力稳定性》中给出了较全面的分析和论述，指出在周期相同的解之间存在着不稳定区域，区分稳定和不稳定的临界状态方程是一个周期性方程，即Mathieu-Hill方程［7］.但是对于大变形的几何非线性压杆，微分方程非常复杂.近些年来，常见结构单元如杆、梁等在轴向周期载荷作用下的振动特性及动力屈曲问题受到广泛研究［8-12］.本文以托卡马克装置圆杆式冷质量支撑结构中的压杆为研究对象，其一端作用有轴向载荷.当整个装置从开始到稳定工作的过程中，假设温度从室温到低温进行周期性变化，讨论压杆在此种工况下的振动稳定区域及失稳临界条件.本文依据Hamilton原理建立了压杆在周期性温度载荷作用下的横向振动方程.根据Floquet理论，讨论了方程的动力学稳定性，得到了第一、二不稳定区域边界；研究了阻尼对不稳定区域大小的影响，随着阻尼的增加，压杆的稳定区域较无阻尼时不断增加，而在某些不稳定区域内并不能单纯依靠增加阻尼来获得动力学稳定.随后我们引入状态反馈控制项，在较大的控制参数范围内，系统处于原不稳定区域的状态被稳定了下来.

1 控制方程

根据文献［4-6］，考虑压杆的长度、直径之比值及结构特点，把压杆简化为一个杆长为的等截面弹性细长杆，如图1所示，在杆顶端作用有轴向载荷P0.

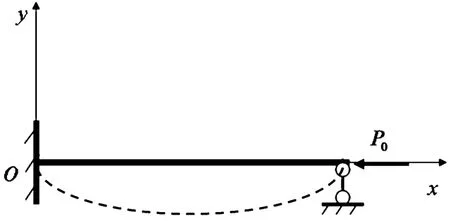
图1 压杆模型示意图Fig.1 The sketch map of a compress rod model

由于超导托克马克装置冷质部件支撑系统在工作过程中一端处于极低温度4.5-80K，而另一端处于室温（300K），因此整个支撑由下向上存在着一个温度梯度.而且，当整个装置从开始到稳定工作的过程中，纵场系统从室温到低温不断变化.现在假设温度场呈周期性变化并且仅沿杆轴线升温，为简化分析，温度梯度函数可设为

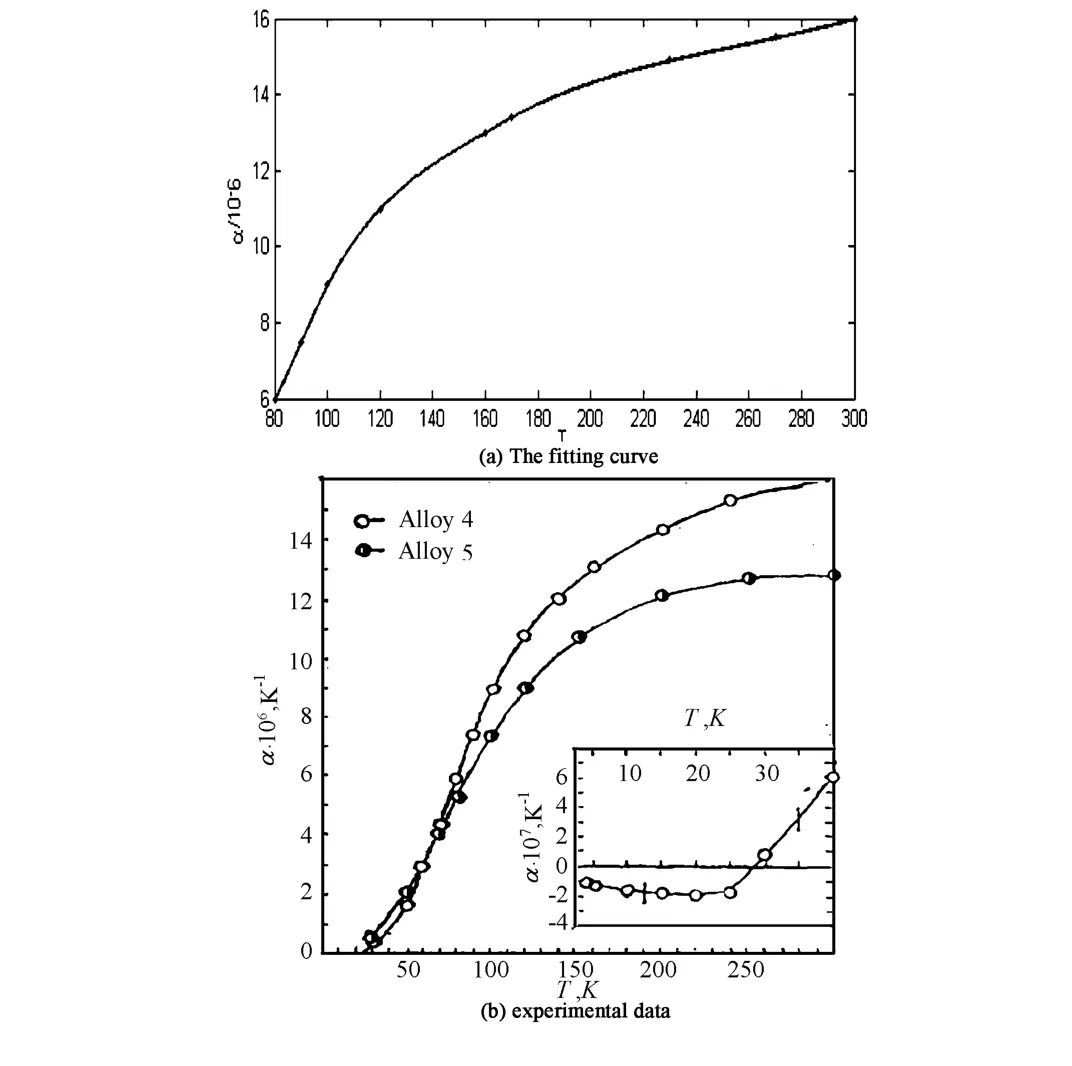
图2 线膨胀系数随温度T的变化（右图来自文献［13］）Fig.2 The curve of linear expansion coefficient of temperature T（figure（b）is from Ref.［13］）

超导托克马克装置冷质部件支撑结构采用奥氏体不锈钢材料304（316LN）.根据实验报道，奥氏体不锈钢材料在5-300K的温度区间内，其线膨胀系数α随温度T呈非线性变化［13］.我们根据实验数据绘制拟合线膨胀系数α随温度的变化曲线，如图2，得到拟合表达式如下：

表1 α（T）表达式中各参数的取值Table 1 Values of the parameters in the expression ofα（T）

以杆剖面中心线为x轴，横向为y轴，设杆在主平面（x，y）内运动.记杆剖面中心线的轴向位移和横向挠度分别为u（x，t）和w（x，t）.采用大位移小变形假设下的Von Karman非线性应变位移关系，同时忽略剪切变形，得到轴向应变

记阻尼系数为C，杆横截面面积、惯性矩、密度分别为A、I、ρ.小变形假设下，材料服从Hooke定律，有

忽略纵向位移的惯性力影响，忽略轴向和转动惯性力，根据Hamilton原理可得到描述压杆横向振动微分方程

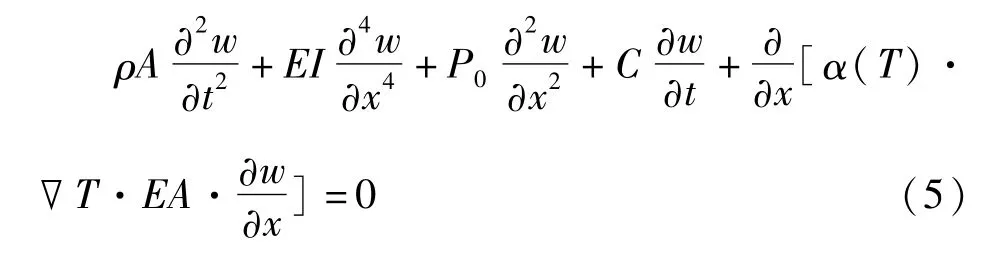
由（1）可得

其中，T0为与初始条件相关的积分常数.

把式（6）、（2）代入式（5）并忽略小量，整理得到

采用Galerkin方法对方程（7）进行分析.参考文献［14］，模态函数 φm（x）取为：

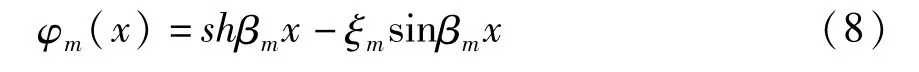
其中，

取w（x，t）＝fm（t）φm（x），仅截断到一阶模态，即m＝1，整理得到

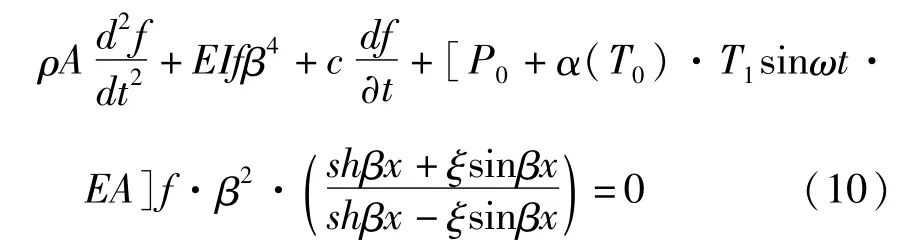
引入固有频率

定义

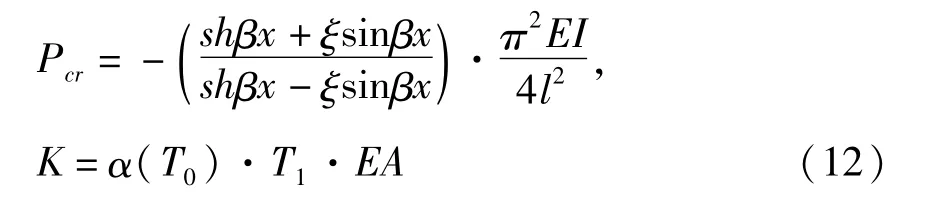
得到以下形式的方程

定义

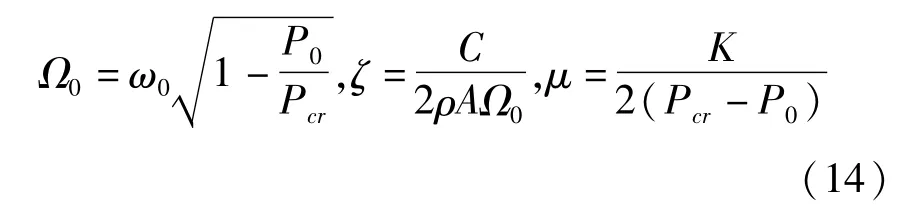
得到无量纲方程

其中μ为激振参数，Ω0为压杆在载荷定值分量作用下的振动频率，ζ为无量纲阻尼系数.

2 稳定性分析

现在讨论方程（15）的稳定区域及失稳临界条件.根据Floquet理论，当方程系数满足一定的关系时，系统可存在周期Ω和2Ω的周期运动，其中Ω动力不稳定区域与稳定区域被具有周期Ω和2Ω的周期解给分隔开，对应于不稳定区域边界的外载荷频率被称为临界频率.

设周期为2Ω的周期解的一般形式为：

取n＝1，得到临界频率方程：

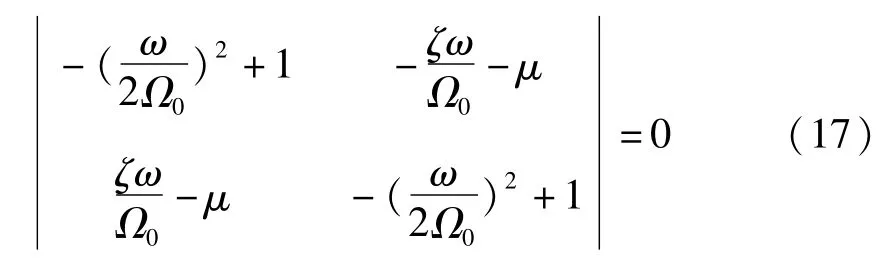
由式（17）可得到压杆第一不稳定区域，其边界近似值为：

当冷质部件支撑结构的设计完成以后，从式（14）可以看出，此时压杆在载荷定值分量作用下的振动频率Ω0是确定的.那么，为保证压杆稳定，外激励的频率ω应满足以下条件

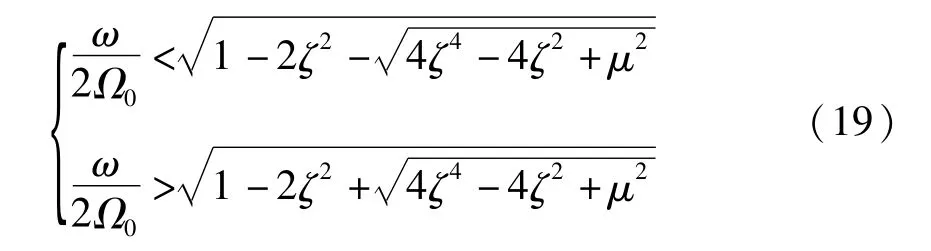
当ζ＝0时，得到无阻尼时压杆的稳定区域和不稳定区域，不稳定区域由曲线包围.增加阻尼，得到当 ζ＝0.1，0.3，0.5时压杆的稳定区域和不稳定区域，如图3（b）所示.随着阻尼的增加，压杆的稳定区域较无阻尼时不断增加；而不稳定区域的依然存在提示我们，此处阻尼的作用并不同于线性阻尼对强迫振动的抑制作用.

图3 压杆在不同阻尼下的第一类不稳定区域边界Fig.3 The first category of unstable region boundary of compress rod under different damping

进一步分析（19），当时，由式（18a）确定的临界曲线不断左移，使得左侧稳定区域不断缩小，式（18）确定的两条临界曲线汇交于一点

在时，汇交点坐标为

类似的，我们分析了压杆在不同阻尼下的第二类不稳定区域边界.设周期为Ω的周期解的一般形式为：

得到临界频率方程：

得到压杆第二不稳定区域边界的近似值为：

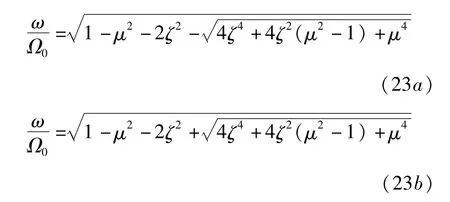
故为保证压杆稳定，外激励的频率ω应满足以下条件

当ζ＝0时，得到无阻尼时压杆的稳定区域和不稳定区域，不稳定区域由曲线＝1包围.增加阻尼，得到当 ζ＝0.1，0.3，0.5时压杆的稳定区域和不稳定区域，如图4（b）所示.随着阻尼的增加，压杆的稳定区域较无阻尼时不断增加.当时，由式（23a）确定的临界曲线不断左移，使得左侧稳定区域不断缩小，由式（23）确定的两条临界曲线汇交于一点.

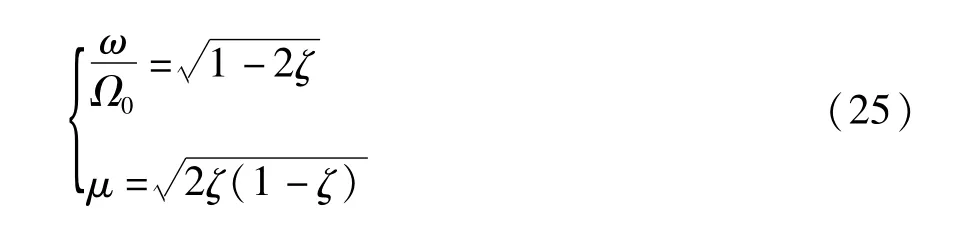
在时，汇交点坐标为

图4 压杆在不同阻尼下的第二类不稳定区域边界Fig.4 The second category of unstable region boundary of compress rod under different damping

3 状态反馈控制分析

给方程（15）加一个状态反馈控制函数H，则系统控制方程成为

其中为反馈系数.

同样根据Floquet理论，得到系统（26）的动力不稳定区域与稳定区域.由临界频率方程

解得第一类不稳定区域的边界近似值为：

由临界频率方程

解得第二类不稳定区域的边界近似值为：

图5给出了当ζ＝0.3，μ＝1时控制系统的第一类、第二类动力不稳定区域.由式（18b）和式（23b）可知，原系统在＜0.906时均处于不稳定状态，图5则展示了在较大的控制参数范围内不稳定状态被稳定了下来.

图5 当ζ＝0.3，μ＝1时控制系统的第一类、第二类动力不稳定区域Fig.5 The first and the second category instability region of the control system whenζ＝0.3，μ＝1

4 结束语

冷质量支撑系统是超导托卡马克装置的一个关键部件，其在工作过程中一端处于低温而另一端处于室温，整个装置从开始到稳定工作的过程中，纵场系统从室温到低温不断变化.本文以托卡马克装置圆杆式冷质量支撑结构中的压杆为研究对象，建立了压杆在周期性温度载荷作用下的横向振动方程，讨论了其动力稳定性，得到了其第一、二不稳定区域边界.研究了阻尼对不稳定区域大小的影响，随着阻尼的增加，压杆的稳定区域较无阻尼时不断增加，而在某些不稳定区域并不能单纯依靠增加阻尼来获得动力学稳定.随后我们引入状态反馈控制项，在较大的控制参数范围内，系统处于原不稳定区域的状态被稳定了下来.

1 Doshi B，Caipin Z，et al.ITER Cryostat-An overview and design progress.Fusion Engineering and Design，2011，86：1924～1927

2 Tado S，Kitamura K，et al.Dynamic analysis of the tokamak support system in ITER.Fusion Engineering and Design，1998，41：421～429

3 潘皖江，武松涛，陈先忠.EAST超导托卡马克装置主机支撑结构极低温条件下应力应变分析.低温与超导，2005，33（3）：29～33（Pan W J，Wu S T，Chen X Z.Stress analysis of the cryogenic support in the EAST superconducting Tokamak device.Cryogenics and Superconductivity，2005，33（3）：29～33（in Chinese））

4 陈先忠，武松涛.有限元在杆式支撑结构力学分析中的应用.核技术，2004，27（7）：557～560（Chen X Z，Wu S T.Application of finite element to the analysis of the bacilliform support structure.Nuclear Techniques，2004，27（7）：557～560（in Chinese））

5 陈先忠，武松涛.HT-7U超导托卡马克冷质部件支撑结构分析.核科学与工程，2003，23（2）：161～164（Chen X Z，Wu S T.Analysis of cryogenic support system for HT-7U superconducting tokamak.Chinese Journal of Nuclear Science and Engineering，2003，23（2）：161～164（in Chinese））

6 陈先忠，武松涛.HT-7U超导托卡马克冷质部件支撑结构方案.核聚变与等离子体物理，2003，23（2）：124～128（Chen X Z，Wu S T.Project of cryogenic support system for the HT-7U superconducting Tokamak.Nuclear Fusion and Plasma Physics，2003，23（2）：124～128（in Chinese））

7 鲍洛金ВВ.弹性体系的动力稳定性.林砚田，姚肇宁译，北京：高等教育出版社，1960（Boliton B B.The dy-namic stability of elastics systems.Tanslated by Lin Yantian and Yao zhaoning，Beijing：Higher Education Press，1960（in Chinese））

8 陈立群，程昌钧.非线性粘弹性柱的稳定性和混沌运动.应用数学和力学，2000，21（9）：890～896（Chen L Q，Cheng C J.Stability and chaoticmotion in columns of nonlinear viscoelastic material.Applied Mathematics and Mechanics，2000，21（9）：890～896（in Chinese））

9 张善元，程国强，韩志军.弹性杆稳定性动力分析与应力波加载杆的动力屈曲.太原理工大学学报，2005，36（2）：111～114，122（Zhang SY，Cheng G Q，Han Z J.Dynamic analysis of stability of elastic bars and its stress wave induced buckling.Journal of Taiyuan University of Technology，2005，36（2）：111～114，122（in Chinese））

10 王春妮，李世荣.热载荷作用下梁的主参数共振及其控制.兰州理工大学学报，2009，35（4）：166～172（Wang C N，Li S R.Primary parametric resonance and control of beams subjected to thermal shock load.Journal of Lanzhou University of Technology，2009，35（4）：166～172（in Chinese））

11 肖刚，李四平.直杆动力屈曲的计算机模拟，上海交通大学学报，2008，42（6）：1005～1008（Xiao G，Li S P.Computer simulation of dynamical buckling for rod.Journal of Shanghai Jiaotong University，2008，42（6）：1005～1008（in Chinese））

12 Esfahani SE，Kiani Y，Eslami M R.Non-linear thermal stability analysis of temperature dependent FGM beams supported on non-linear hardening elastic foundations.International Journal of Mechanical Sciences，2013，69：10～20

13 范光汉译.奥氏体不锈钢和钛合金在5～300K的热性参数.低温与特气，1986，1：51，52～53（Skibina L V，Llichey V Ya，et al.Thermal expansion of the austenitic stainless and titanium alloys in the temprature range 5～300K.Cryogenics，1985，25（1）：31～32（in Chinese））

14 刘延柱，陈文良，陈立群.振动力学.北京，高等教育出版社，2000（Liu Y Z，Chen W L，Chen LQ.Mechanic of vibration.Beijing：Higher Education Press，2000（in Chinese） ）