基于滑模控制的充液航天器燃料晃动抑制研究*

顾黄兴 齐瑞云

（南京航空航天大学自动化学院，南京 210016）

引言

充液航天器是一类携带大量液体燃料、液体冷却剂的刚-液耦合复杂非线性系统［1］，有国内外航天试验机构研究表明，航天器在发射、变轨、发动机启停等阶段，自身会发生频繁的振动［2］.这种结构振动极易与贮箱内液体燃料的晃动相交耦，交耦后自由液面的非线性运动会对刚体航天器产生显著的干扰力、干扰力矩及冲击压力［3］，对航天器的姿态控制和稳定性产生重大影响.因此，控制系统的设计需要综合考虑液体晃动的影响，在控制航天器姿态及运动的同时，也要抑制液体燃料的晃动.由于航天器不能直接对液体燃料施加控制，只能通过刚体航天器与液体燃料之间的耦合作用来抑制液体的晃动，这样系统的控制输入个数小于系统的自由度，使得整个航天器系统表现为一个欠驱动系统，需要由较少的控制输入控制较多的系统自由度［4］.作为一类特殊的非线性系统，对欠驱动系统的研究对于非线性控制研究和非线性动力学研究都具有重要的价值［5］.

目前，国内外研究的充液航天器一般是一类零重力条件下，燃料贮箱一般为规则的几何形状，如球形或者椭球形的轴对称刚体航天器.刚-液耦合动力学方程的求解方法有受力分析法［6］，及Lagrange-Euler方程解法两种［7］，系统姿态控制方案有：非线性反馈控制［8-9］，基于无源性的方法［10］，自适应极点配置控制［6-7］，分层滑模控制方法［12］，自适应动态逆控制方法［13］等.由于滑模控制对非线性对象有着较强的控制作用，并且有着响应迅速，对建模误差，参数不确定和扰动不敏感，物理实现简单等优点，因此，本文考虑使用滑模控制方法来实现这一类充液航天器的控制.

文献［12］提出的分层滑模控制方案，首先将系统分成两个子系统，分别设计滑模面，并由其构成第二层滑模面，然后进行控制器的设计.不过这种方法要求两个子系统的滑模面乘积符号为恒定值，在实际应用或仿真中可能不能满足这一条件.文献［14］针对一类欠驱动系统提出了一种滑模控制方案，实现了对系统的稳定控制，取得了较好的控制效果.本文参考这一种滑模控制方案，首先将系统进行一定的转换，将系统的一部分化成一定形式的标准型，另一部分经过一定的假设和设计，可以用来作为标准型的外部输入，最后针对这一标准型设计了一个滑模控制器，实现了对系统的稳定控制.仿真结果表明了该滑模控制器的有效性和可行性.

1 系统模型

本节给出了带单个液体燃料贮箱的航天器的动力学方程并将其做了一定的转化.其中，航天器作为一个刚体，其内部贮箱包含有液体燃料，液体燃料的晃动可以用单摆模型来等效.如图1所示，考虑刚体航天器在固定平面OXZ上的作动.其中，vx和vz分别代表航天器在轴向和横向的速度分量；θ表示航天器姿态角，即航天器体坐标系Oxz相对惯性坐标系OXZ转过的角度；ψ是等效单摆相对于航天器轴向的摆角，表征液体燃料的晃动.航天器控制力及力矩有三个：推力F，作用于航天器末端并沿着航天器轴向经过质心；横向推力f，作用于航天器侧向并通过质心；使航天器围绕质心转动的控制力矩M.

图1 充液航天器示意图Fig.1 The sketch of the spacecraftwith fuel slosh

如图1所示，刚体航天器的质量为m，液体燃料质量为mf，等效单摆摆长为a，相对于航天器质心的转动惯量为If.坐标系原点到航天器质心距离为b，液体晃动的阻尼系数为ε，在本文中，考虑这些参数为固定值的情况.

由文献［9］可知，此刚体航天器的动力学方程为

考虑推力F为常值的情况，并且在航天器作动时，可以假设在航天器姿态角变化和液体晃动幅度较小时，航天器的轴向加速度变化不大，可以假定为常量，这在后面仿真中进行了验证.因此，可以将方程（1）简化为

并且，由（3）式可得

其中，ax，az分别为航天器的轴向和横向加速度.将式（5），（6）代入方程（2），（4），可以得到

下面将系统模型转化成一定形式的标准型，以方便后面滑模控制器的设计.

2 模型转化及分析

2.1 模型标准型

考虑将系统（7），（8）作为一个子系统，其输入为，输出为θ和ψ，此系统为一个欠驱动系统.文献［15］介绍了一种系统的方法，可以将一些欠驱动系统转化为满足某种结构的标准型.

令代入方程（7），（8），则有

进一步可以将其整理为

其中

由此，系统（1）～（4）可以整理为：

其中

如果控制力矩M和横向推力f为0，轴向推力F为恒定值，那么可以定义系统（1）～（4）的一个相对平衡点为：

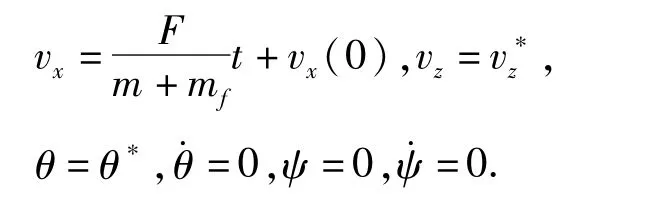
其中和θ*为任意常量，vx（0）为航天器的初始轴向速度.不失一般性，可以选择＝0，θ*＝0，即系统（10）的相对平衡点为

2.2 模型性质分析

可以验证，函数f1（x）满足如下的一些性质.

（1）f1（0，0，0，0）＝0.

（2）∂f1/∂x4＝-

（3）f1（0，0，x3，x4）＝0是渐近稳定流形，即在f1（0，0，x3，x4）＝0时，x3，x4会趋于0.

下面进行对验证过程进行简要陈述.

（1）由于并且＝x2-x4＝0，在后面设计中，当t→∞时，会设计使即有0.将其代入f1（x），则有f1（0，0，0，0）＝0.

（2）由于则cos x3∈［0，1］，则有

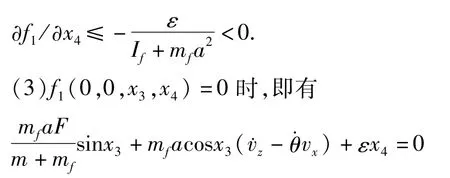
将代入，可得

将代入，整理得到，

求解此微分方程，当x3＝0时当x3≠0时，可得，

两边分别积分，可得

进一步可以写成，

其中，c为常数.根据对数函数性质可知，当t→∞时，｜sin x3｜mfavx-ε｜1-cos x3｜ε→0.在本文的航天器系统中，mfavx-ε＝0，因此，根据三角函数性质可知当t→∞时，x3→0，即有x4→0，因此，f1（0，0，x3，x4）是渐近稳定流形.在下面的设计及分析过程中将会用到f1（x）的这些性质.

3 滑模控制器设计

本文采用文献［14］的方法设计滑模控制器，控制目标是使航天器的横向速度和姿态角达到平衡点，同时抑制液体燃料的晃动，使航天器达到渐近稳定.

为了达到控制目标，设计控制输入M为

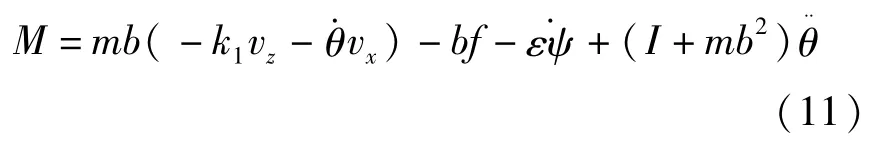
将其代入式（6），可以得到 ˙vz＝-k1vz，显然选择合适的正常量k1可以使vz渐近稳定.这样在接下来的设计过程中，就可以将vx，vz看成外部变量来进行设计.

针对系统（9），接下来设计u，使得x→0，我们将采用滑模控制的方法来设计控制器.

定义误差变量为

其中定义E1是为了后面方便研究和分析系统的稳定性.

由于∂f1/∂x4恒为负值，可以定义滑模面为s＝c1e1+c2e2+e3.其中参数c1，c2满足如下的条件：

A1＝是Hurwitz矩阵.

令＝0，可以设计等效控制量为：

其中，

设计切换控制量使得s→0，

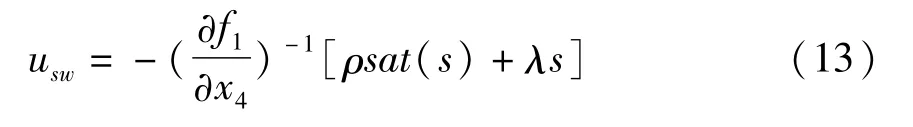
其中ρ，λ为选定的正常量，并且当｜s｜≤0.1时，sat（s），｜s｜＞0.1时，sat（s）＝0.1sign（s），其中，

因此，设计的滑模控制器为：

4 稳定性分析

选择Lyapunov函数为对其求导，并将式（12）～（14）代入，可以得到

当且仅当s＝0时因此，在滑模控制器的作用下，滑模面s将在有限时间内将达到0.在s＝0或e3＝-c1e1-c2e2时，系统（9）退化为

由于A1为Hurwitz矩阵，系统（15）渐近稳定.因此，e1＝x1，e2＝x2将渐近收敛到0.即可以有s＝0，e3＝f1＝0.由之前验证过的f1（x）的性质（3）可知，x3，x4也将能够收敛到平衡点0，即 ψ＝x3＝0，θ＝x1-x3＝0.

由此，可以证明设计的滑模控制器可以在有限时间内，使航天器的姿态角，横向速度及等效摆角都达到平衡点，达到了设计目的.

5 仿真

针对本文使用的滑模控制器，本节采用数字仿真来验证其对这类充液航天器的控制效果.

仿真中采用的航天器及燃料的物理参数为［9］：

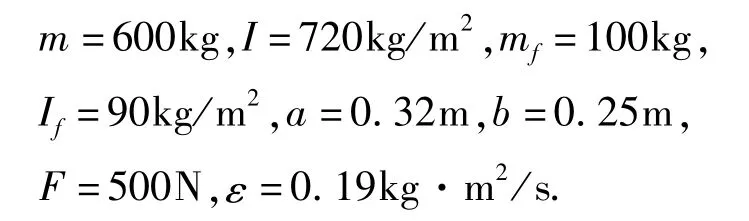
设计的控制器参数为：

系统状态的初始值为：

仿真结果如图（2）-（4）.

图2 vx，vz的响应曲线Fig.2 Time responses of vx and vz

图3 s，ψ及θ的响应曲线Fig.3 Time responses of s，ψ，andθ

从仿真结果可以看到，控制器可以使系统渐近稳定.从图2中可以看出，航天器的轴向速度保持恒定的加速度，符合前文中的假设.图2和3中，航天器的各个状态量和滑模面都能够很快达到平衡点.从图4中也可以看出，系统的控制量，即横向推力和控制力矩变化曲线比较平滑.因此，在设计的滑模控制器作用下，航天器的横向速度，姿态角以及等效单摆的摆角都能够达到平衡点，实现了航天器系统的渐近稳定，达到了预期的控制目标.

图4 控制输入f，MFig.4 Control inputs f and M

6 结论

针对一类带液体燃料晃动的航天器，本文采用了一种滑模控制的方法设计了控制器.首先将系统模型转化为一定形式的标准型，并验证其系统函数满足某些关键的设计条件，在此基础上进行控制器的设计.由于系统本身表现为一个欠驱动系统，设计的控制器可以使系统的一些状态量达到平衡点时，而剩下的状态量在系统自身的作用下也能达到平衡点，从而使整个航天器系统渐近稳定.仿真结果表明，采用这种方法设计的滑模控制器能够实现控制目标，证明了所设计的控制器的有效性及可行性.

1 杨旦旦，岳宝增.求旋转椭球形贮箱内液体小幅晃动基频的一种新方法.动力学与控制学报，2011，9（3）：249～252（Yang D D，Yue B Z.Solving the firsteigenfrequency of liquid sloshing in ellipsoidal tanks using analytical method.Journal of Dynamics and Control，2011，9（3）：249～252.（in Chinese））

2 次永伟，邱大芦，付乐平，邵小平.航天器振动试验控制技术进展.动力学与控制学报，2014，12（3）：193～200（Ci YW，Qiu D L，Fu L P，Shao X P.Progress in spacecraft vibration testing control technology.Journal of Dynamics and Control，2014，12（3）：193～200（in Chinese））

3 尹立中，王本利，邹经湘.航天器液体晃动与液固耦合动力学研究概述.哈尔滨工业大学学报，1999，31（2）：118～122（Yin L Z，Wang B L，Zou JX.Introduction of Liquid Sloshing and Liquid-solid Coupled Dynamics of Spacecraft.Journal of Harbin Institute of Technology，1999，31（2）：118～122（in Chinese））

4 周祥龙，赵景波.欠驱动非线性控制方法综述.工业仪表与自动化装置，2004，（4）：10～14（Zhou X L，Zhao J B.A survey on nonlinear controlmethod of underactuated.Industrial Instrumentation and Automation，2004，（4）：10～14（in Chinese））

5 王伟，易建强，赵冬斌，等.Pendubot的一种分层滑模控制方法.控制理论与应用，2006，22（3）：417～422（Wang W，Yi JQ，Zhao D B，etal.Hierarchical slidingmode control of pendubot.Control Theory and Applications，2006，22（3）：417～422（in Chinese））

6 Shageer H，Tao G.Modeling and adaptive controlof spacecraft with fuel slosh：overview and case studies.AIAA Guidance，Navigation and Control Conference and Exhibit，2007：1～19

7 梁琼，岳宝增，于丹.充液航天器目标跟踪自适应控制.空间控制技术与应用.2011，37（01）：40～44（Liang Q，Yue B Z，Yu D.Adaptive control of target tracking for liquid-filled spacecraft.Aerospace Control and Application，2011，37（01）：40～44（in Chinese））

8 岳宝增.充液柔性航天器非线性姿态动力学及再定向姿态机动.动力学与控制学报，2010，8（01）：74～79（Yue B Z.Nonlinear attitude dynamics and reorientation maneuver for completely liquid-filled flexible spacecraft.Journal of Dynamics and Control，2010，8（01）：74～79（in Chinese））

9 Reyhanoglu M.Maneuvering control problems for a spacecraftwith unactuated fuel slosh dynamics.In：Proceedings of 2003 IEEEConference on Control Applications.Turkey：Istanbul Technical University，2003：695～699

10 Reyhanoglu M，Hervas JR.Nonlinear dynamics and control of space vehicles with multiple fuel slosh modes.Control Engineering Practice，2012，20（9）：912～918

11 杜辉.基于无源性的带液体晃动月球着陆器的姿态控制.空间控制技术与应用，2011，37（1）：50～54（Du H.Passivity based attitude control for lunar lander with fuel sloshing.Aerospace Control and Application，2011，37（1）：50～54（in Chinese））

12 杜辉，张洪华.一类带液体晃动航天器的姿态控制.空间控制技术与应用，2010，36（2）：25～30（Du H，Zhang H H.Attitude control for a kind spacecraftwith fuel slosh.Aerospace Control and Application，2010，36（2）：25～30（in Chinese））

13 祝乐梅，岳宝增.充液航天器姿态的自适应非线性动态逆控制.动力学与控制学报，2011，9（4）：321～325（Zhu LM，Yue B Z.Adaptive nonlinear dynamic inversion control for spacecraft attitude filled with fuel.Journal of Dynamics and Control，2011，9（4）：321～325（in Chinese））

14 Xu R，Ozguner U.Slidingmode control of a class of underactuated systems.Automatica，2008，44（1）：233～241

15 Olfati-Saber R.Normal forms for underactuated mechanical systems with symmetry.IEEE transactions on automatic control，2002，47（2）：305～308