位形空间中约束力学系统的Lagrange对称性与守恒量*

刘学锋 张斌 方建会

（1.中国石油大学（华东）理学院，青岛 266580）（2.大庆油田工程建设公司安装公司，大庆 163450）

引言

对称性是数学、物理等学科领域内非常重要的法则之一.对称性理论也是近代分析力学研究的主要方向之一，Noether对称性、Lie对称性和Mei对称性一直是对称性理论研究的主要对象.近年来，人们对Noether、Lie和Mei对称性的研究成果丰硕，理论体系已经比较完善，寻求和研究新型对称性是对称性理论发展的要求.Lagrange对称性作为新型对称性的一种，相对于Noether、Lie和Mei对称性，Lagrange对称性理论不够完善.20世纪六七十年代Currie等对不同自由度［9，10］Lagrange函数等价问题的研究是人们对Lagrange对称性的最早探索，上世纪70年代末到90年代，Lutzky等对力学系统的Lagrange函数等价问题做了一系列的研究［11-14］，Hojman将这种Lagrange函数等价关系称为Lagrange对称性［14，15］，Lagrange对称性现已被推广到Hamilton、Birkhoff等系统［15-26］.赵跃宇等人是我国最早研究Lagrange对称性的学者［15］.本文根据力学系统运动微分方程的特点，将广义非完整约束反力，广义反推力等系统可能受到的力看做一合力，然后研究两个系统运动微分方程的Lagrange对称性.以便讨论位形空间中任意两种系统的微分方程满足Lagrange对称性的定义和判据，以及Lagrange对称性导致守恒量的条件和守恒量形式.

1 位形空间中力学系统的统一动力学方程

设某一系统的Lagrange函数为L，系统所受非势力的合力为F，则系统动力学方程为

另一不同于上述系统的Lagrange函数为系统所受非势力合力为则系统动力学方程为

其中fs和分别为系统的广义非势力，广义约束反力等力的广义合力在广义坐标qs方向上的分量，即

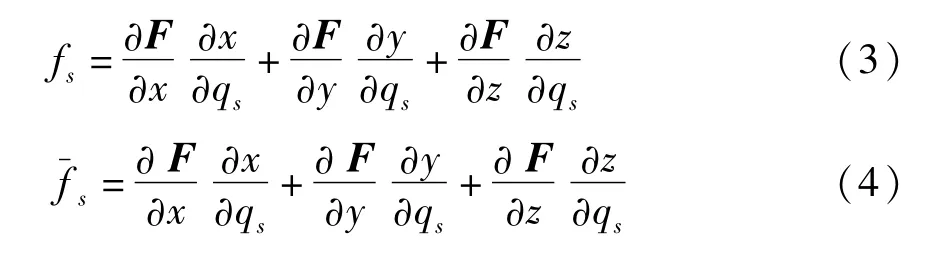
2 系统的Lagrange对称性

对于给定系统（1）和（2）的两组动力学函数L，f和定义Lr和分别为

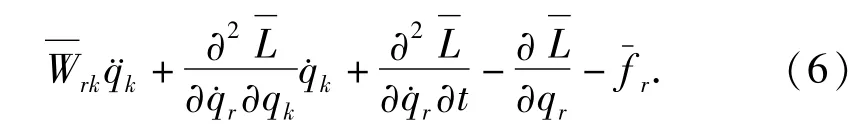
其中

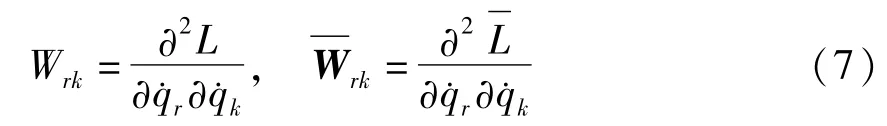
引入

并称之为Lagrange算子，则

定义对于系统（1）和（2），如果由动力学函数L和f确定的

的每一个解都满足由动力学函数确定的

反之亦然，则表明两系统之间具有Lagrange对称性.

由式（10）和（12）得

其中

把（13）式代入（11）式，并考虑到（9）式得

由定义和（15）式得

判据：对于系统（1）和系统（2），如果两组动力学函数和L，f满足方程（15），则两系统之间具有Lagrange对称性.

3 Lagrange对称性导致的守恒量

对于两系统的Lagrange对称性有如下命题：

命题 对于系统（1）和系统（2），如果两组动力学函数L，f和满足条件

则系统的Lagrange对称性可导致守恒量

其中A为以为元素的矩阵，

证明： 将（18）式代入（15）式得

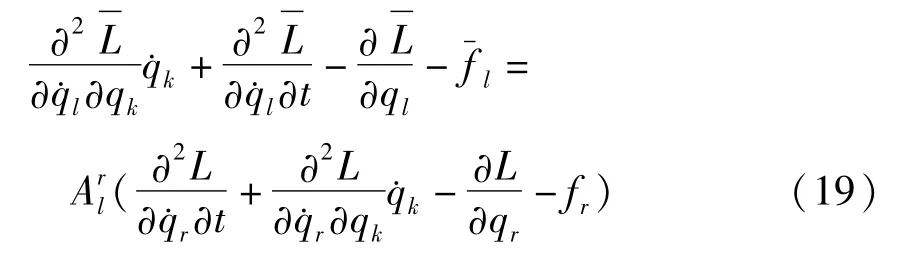
对（19）式求关于的偏导数得

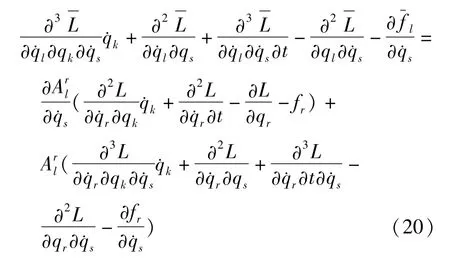
联立（9）式和（11）式得

将（21）式代入（20）式得

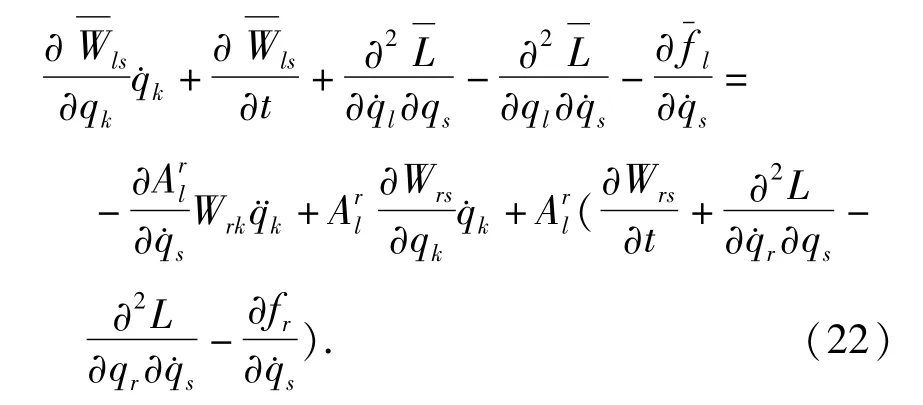
对求关于的偏导数

曹志成等[13]采用转底炉直接还原工艺，“转底炉直接还原- 燃气熔分”及“转底炉直接还原- 磨矿磁选”流程处理铜渣均可获得锌品位60.02%的氧化锌粉尘。曹志成等[14]采用转底炉直接还原和磨矿- 磁选工艺流程，所得最佳还原条件为铜渣∶无烟煤∶石灰石∶工业纯碱=100∶21.5∶10∶1，还原温度1 280 ℃，还原时间38 min；在布袋收尘系统所得粉尘中氧化锌含量为74.25%。

即

由（18）式得

求（25）式关于的偏导数得

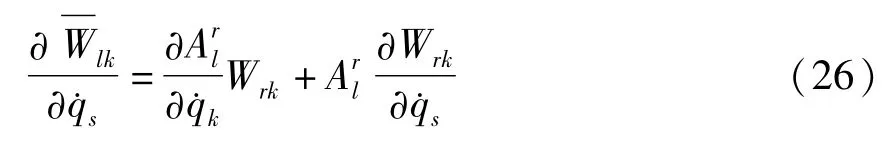
由（24）和（26）式得

把（27）和（28）式代入（22）式得

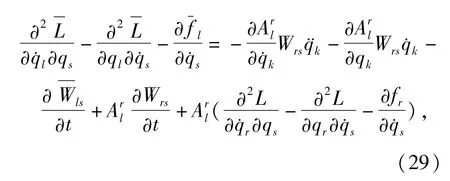
即

由式（28）得

将（31）式代入（30）式得

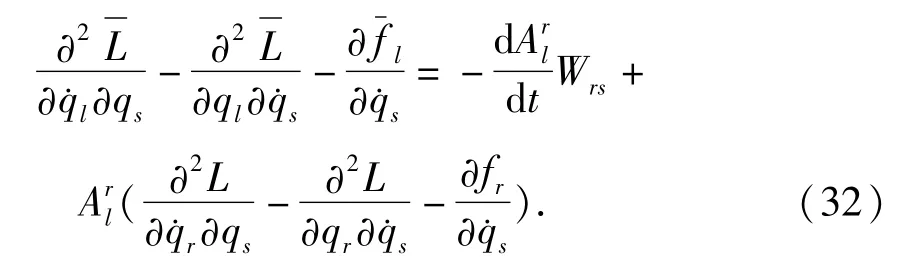
将条件（16），（33）和（34）式代入（32）式，得

因为T和为反对称矩阵，U和为对称矩阵，因此对于任意正整数m有

根据矩阵的特性及矩阵迹的性质得

即

即

可得（17）式，命题 得证.

4 算例

设某系统的Lagrange函数为

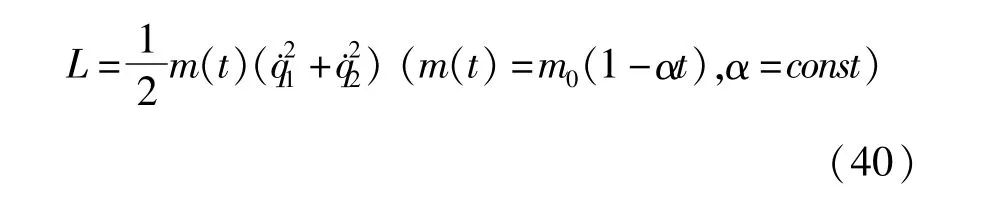
系统所受各类广义力合力的分量分别为

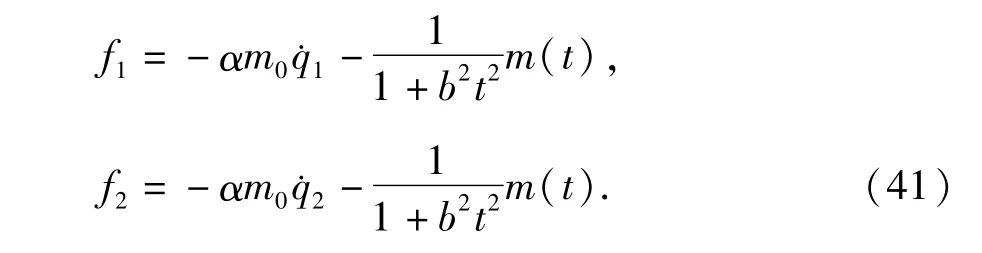
试研究系统的Lagrange对称性及其导致的守恒量.

则根据（9）式和（10）式得

假设有另一系统，其性质与系统（40）不同，其Lagrange函数为

其各类广义力合力的分量分别为

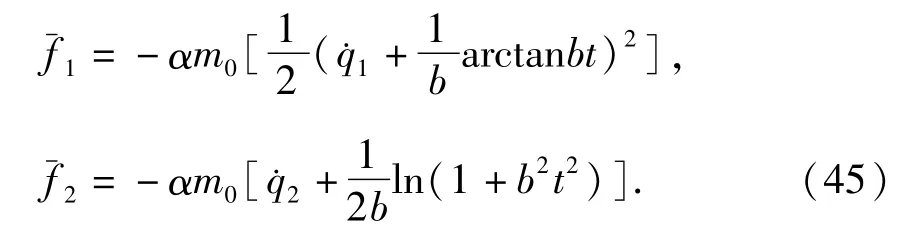
则由（10）得分别为

将（45）式代入（46）式和（47）式，得

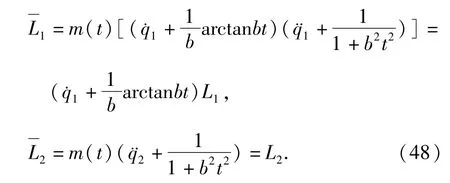
并且可以得到

易知（45）式和（41）式满足条件（16），故由命题得守恒量

5 小结

本文讨论了位形空间中约束力学系统统一动力学方程的Lagrange对称性理论，给出了位形空间中约束力学系统统一动力学方程的Lagrange对称性判据和导致守恒量的条件以及守恒量形式.本文给出的结论不仅可以研究同类系统的Lagrange对称性，而且可以研究两个不同性质力学微分方程的Lagrange对称性.当系统方程中的fs为非完整约束反力，广义反推力和广义非势力之和时，讨论系统变为变质量非完整系统，即本文结论为文献［25］的结果；当系统方程中的fs为非完整约束反力和广义非势力之和时，则研究系统为非完整系统，本文结论将与文献［17］的结果相符.

1 Guo Y X，Shang M，Luo SK.Poincare-cartan integral invariants of Birkhoffian systems.Applied Mathematics＆Mechanics，2003，24（1）：68～72

2 Mei F X，Xu X J，Zhang Y F.A unified symmetry of Lagrangian system.Acta Mechanica Sinica，2004，20（6）：668～671

3 梅凤翔.约束力学系统的对称性与守恒量.北京：北京理工大学出版社，2004（Mei F X.Symmetries and conserved quantities of constrained mechanical systems.Beijing：Beijing Institute of Technology Press，2004（in Chinese））

4 Fang JH，Chen P S，Zhang J.Form invariance and Lie symmetry of variable mass nonholonomic mechanical system.Applied Mathematics＆Mechanics，2005，26（2）：204～209

5 Cai J L.Conformal invariance and conserved quantities of general holonomic systems.Chinese Physics Letters，2008，25（5）：1523～1526

6 Fu JL，Wang X J，Xie FP.Conserved quantities and conformal mechanico-electrical systems.Chinese Physics Letters，2008，25（7）：2413～2416

7 张伟伟，方建会，张斌.事件空间离散完整系统的Noether理论.动力学与控制学报.2012，10（2）：117～120（Zhang W W，Fang JH，Zhang B.Noether theorem of discrete holonomic systems in event space.Journal of Dynamics and Control，2012，2（2）：117～120）（in Chinese））

8 梅凤翔.关于力学系统的守恒律.北京理工大学学报，2002，22（2）：133～138（Mei F X.On conservation laws ofmechanical system.Journal of Beijing Institute of Technology，2002，22（2）133～138（in Chinese））

9 Currie D G，Saletan E J.Q-equivalent particle Hamiltonians.I.The classical one-dimensional case.Journal of Mathematical Physics，1966，7（6）：967～974

10 Hojman S，Harleston H.Equivalent Lagrangians：multidimensional case.Journal Mathematical Physics，1981，22（7）：1414～1419

11 Sarlet W.Note on equivalent Lagrangians and symmetries.Journal of Physics A：Mathematical and General，1983，16（7）：L229～L233

12 Lutzky M.Orgin of non-noether invariants.Physics Letters，1979，75A：8～10

13 SarleW.Symmetries and alternative Lagrangians in higher-ordermechanics.Physics Letters，1985，108A（1）：14～18

14 Hojman S.Symmetries of Lagrangians and of their equations of motion.Journal of Physics A：Mathematical and General，1984，17（12）：2399～2412

15 赵跃宇，梅凤翔.力学系统的对称性与不变量.北京：科学出版社，1999（Zhao Y Y，Mei F X.Symmetries and invaiants of mechanical systems.Beijing：Science Press，1999（in Chinese））

16 Mei F X，Gang T Q，Xie J F.A symmetry and a conserved quantity for the Birkhoff system.Chinese Physics，2006，15（8）：1678～1681

17 Mei F X，Wu H B.Symmtry of Lagranians of nonhomonolic system.Physics Letters A，2008，372：2141～2147

18 梅凤翔，吴惠彬.相对运动动力学系统的Lagrange对称性.物理学报，2009，58（9）：5919～5923（Mei FX，Wu H B.Lagrange symmetry for a dynamical system of relative motion.Acta Physica Sinica，2009，58（9）：5919～5923（in Chinese））

19 Wu H B，Mei FX.Symmetry of Lagrangians ofholonomic system in terms of quasi-coordinates.Chinese Physics B，2009，18（8）：3145～3149

20 张毅.广义Birkhoff系统的Birkhoff对称性与守恒量.物理学报，2009，58（11）：7436～7439（Zhang Y.Birkhoff symmetries and conserved quantities of generalized Birkhoffian systems.Acta Physica Sinica，2009，58（11）：7436～7439（in Chinese））

21 张毅，葛伟宽.非Chetaev型非完整系统的Lagrange对称性与守恒量.物理学报，2009，58（11）：7447～7451（Zhang Y，Ge W K.Lagrange symmetries and conserved quantities for nonholonomic systems of non-Chetaev’s type.Acta Physica Sinica，2009，58（11）：7447～7451（in Chinese））

22 Wu H B，Mei F X.Symmetry of Lagrangians of nonholonomic systems of non-Chetaev＇s type.Chinese Physics B，2010，19（3）：030303

23 Xia L L，Cai JL.Symmetry of Lagrangians of nnholonomic crollable mchanical systems.Chinese Physics Letters，2010，27（8）：080201

24 张毅.非完整力学系统的Hamilton对称性.中国科学：物理学，力学，天文学，2010，40（9）：1130～1137（Zhang Y.Symmetry of Hamiltonians of nonholonomic mechanical system.Scientia Sinica Physics Mechanics＆Astronomy，2010，40（9）：1130～1137（in Chinese））

25 张斌，方建会，张克军.变质量非完整系统的Lagrange对称性与守恒量.物理学报，2012，61（2）：021101（Zhang B，Fang JH，Zhang K J.Symmetry and conserved quantity of Lagrangians for nonholonomic variablemass system.Acta Physica Sinica，2012，61（2）：021101（in Chinese））

26 Zhang B，Fang JH，Zhang W W.Symmetry of Lagrangians of holonomic nonconservative system in event space.Chinese Physics B，2012，21（7）：070208

27 张斌.约束Lagrange体系的Lagrange对称性与守恒量的研究［硕士学位论文］.青岛：中国石油大学（华东），2013（Zhang Bin.Symmetry of Lagrangians and conserved quantity for constrained Lagrangians system［Master Thesis］.Qingdao：China University of Petroleum（East China），2013（in Chinese））

28 张克军，方建会，李燕，张斌.一般离散完整系统Mei对称性的精确不变量与绝热不变量.动力学与控制报，2010，8（4）：311～315（Zhang K J，Fang J H，Li Y，Zhang B.Exact invariants and adiabatic invariants of general discrete holonomic system.Journal of Dynamics and Control，2010，8（4）：311～315（in Chinese） ）