带集中质量复合材料层合屈曲梁参激振动的研究*

陈得良 付钦 钱长照

（1.长沙理工大学土木与建筑学院，长沙 410014）（2.厦门理工学院土木工程与建筑学院，厦门 361021）

引言

近年来，梁被广泛运用于机械，土木，航天等工程结构中，其非线性动力学行为也在这些结构中频繁的出现，并对结构的安全性，适用性和耐久性产生了重要影响.因此，研究梁的非线性振动特性对于合理设计和利用工程结构具有非常重要的意义.自Tseng［1］首次发现简谐激励下屈曲梁的混沌运动后，许多学者对梁的非线性动力学特性产生了浓厚的兴趣并展开了丰富的研究.Emam和Nayfeh［2］用打靶法分析了两端固定且受横向周期激励屈曲梁主共振下的周期解，讨论了周期解的稳定性和分叉点问题，其理论结果与实验结果［3］相吻合.季进臣［4］用实验方法研究了一端固定，一端滑动受轴向简谐激励的参激屈曲梁的动力学问题，并获得了动态响应在参数平面上的分布规律以及非线性阻尼对分布区域的影响.姚志刚，张萌［5］研究了简支压电复合材料层合梁在轴向、横向载荷共同作用下非线性动力学、分叉和混沌动力学响应，分析了各种参数对倍周期分叉的影响及变化规律.然而上述研究主要针对没有集中质量的屈曲梁.而实际工程中很多梁结构都带有一个或者多个集中质量，且集中质量的大小和位置会对梁的一阶频率，振型以及非线性特性产生重要影响，因此有部分学者针对这种带集中质量的梁的非线性动力学问题开展了研究.Ozkaya［6］研究了弹性地基上带一个集中质量两端固定的微弯曲梁的横向振动问题，绘出了不同质量下的幅频特性曲线，讨论了集中质量对横向振动的影响.Saito［7］采用谐波平衡法研究了带集中质量受横向简谐激励简支梁的强迫振动，讨论了集中质量的大小和位置对系统一阶频率的影响.尽管针对带集中质量梁的非线性振动问题有部分研究，然而主要研究的是系统的横向自由振动或者强迫振动问题，而对其他方面的研究则较少见到.

本文基于欧拉梁理论，研究了带一个集中质量一端固定一端夹支受轴向周期激励的复合材料层合屈曲梁的非线性动力学行为，得到了集中质量的大小和位置对系统一阶频率和倍周期分叉解的影响，分析了主共振下系统随激励幅值变化的运动规律，为合理设计工程构件提供了有益的参考.

1 动力学方程的建立

如图1所示一端固支一端夹支复合材料层合梁，梁长为L，宽为b，高为h，梁的密度为 ρ0，阻尼系数为c.梁在夹支端承受如图所示的轴向周期荷载，其大小为p0-p1cosΩt，其中p0为轴向静压力，其值大于临界屈曲荷载，p1为激励幅值，Ω为外激励频率，集中质量m1.

图1 带集中质量屈曲梁模型Fig.1 Themodel of a buckled beam with a lumped mass

由弹性梁理论，任意时刻内各点位移设为

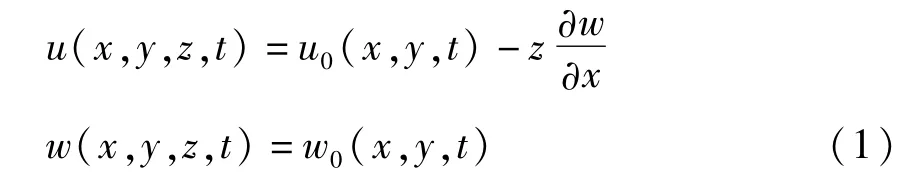
式中u0，w0分别为梁中面上任意一点位移，u，w则为梁截面水平和竖直方向任意一点位移.

考虑对称铺设复合材料层合梁，并定义梁内力关系［8］如下：

其中

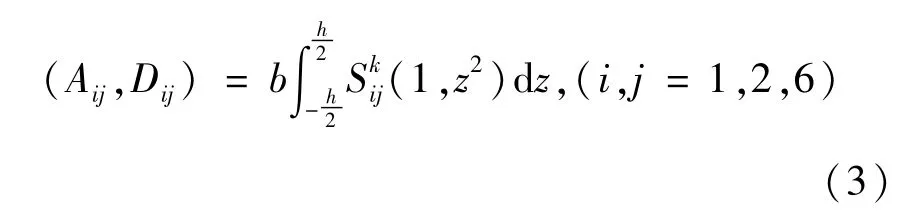
Aij为薄膜刚度，Dij为弯曲刚度为第k层弹性刚度.

引入Reissner函数：

式中B（σij代表弹性体的余能密度，fi为沿坐标轴i方向上每单位面积内的体力，V为沿坐标轴方向上每单位表面积所承受的表面力，Ap为弹性体所占空间，为弹性体表面上面力作用面积.

对于图示结构，其内力势能为

由达朗贝尔原理，将惯性力-ρ0ui，tt作为分布力，并忽略轴向惯性项，则横向惯性力产生的外力势能

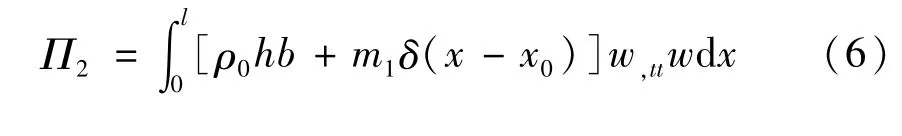
式中x0为集中质量在梁上的位置.

不计梁自重，则阻尼力产生的外力势能

由 δΠ＝0得

边界条件

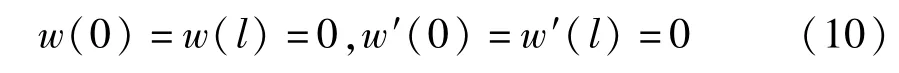
在x＝l处，力的边界条件

将式（11）代入式（9）可得运动微分方程

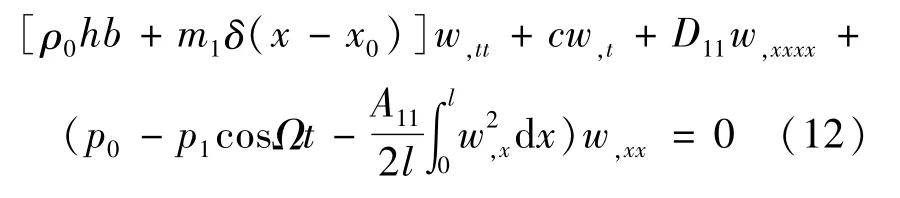
设梁的静位移为ws，将其代入式（12）得

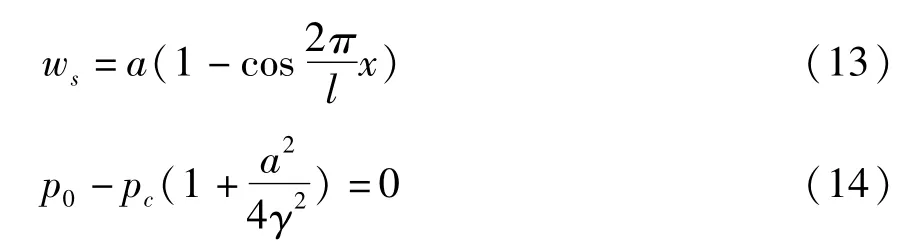
其中为一阶临界屈曲荷载，γ＝为回转半径.

截取一阶屈曲模态，设其振型函数为φ＝（1-，则屈曲梁的总位移为

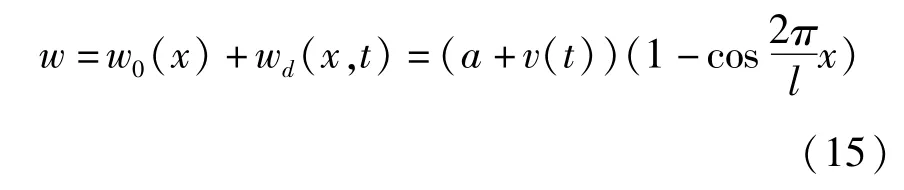
将式（14）、（15）代入式（12），并在梁全长范围内进行伽辽金积分，可得

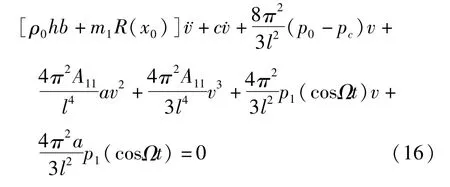
式中

引入无量纲变量

对式（16）进行无量纲化后得：

其中

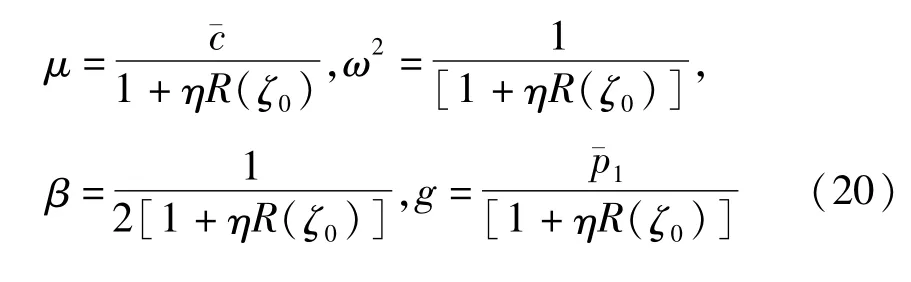
2 数值模拟

对式（19）进行变换得

利用四阶龙格—库塔法对式（21）进行数值模拟，可得不同参数下屈曲梁的非线性动力学特性.

2.1 集中质量位置对系统一阶频率的影响

由式（20）可知，系统的一阶频率受集中质量位置和大小的影响，当集中质量的位置和大小变化时，系统的一阶频率也会随之变化.图2研究了集中质量位置对系统一阶频率的影响.图中横轴为集中质量位置与梁跨径的比值，其值为0到1，纵轴是系统的一阶频率.不难发现，集中质量的位置对系统一阶频率的影响是关于梁跨中对称分布的，跨中处一阶频率最小，越靠近跨中，系统的一阶频率越小，反之就越大.

图2 集中质量位置与系统一阶频率关系Fig.2 The relationship between the locations of the lumped mass and the natural frequency

2.2 集中质量大小对系统一阶频率的影响

图3研究了集中质量大小对系统一阶频率的影响.其中横轴是集中质量与梁的质量比值，纵轴为一阶频率.由图可知，系统的一阶频率随集中质量的增加而逐渐减小，集中质量越大，系统的一阶频率越小.

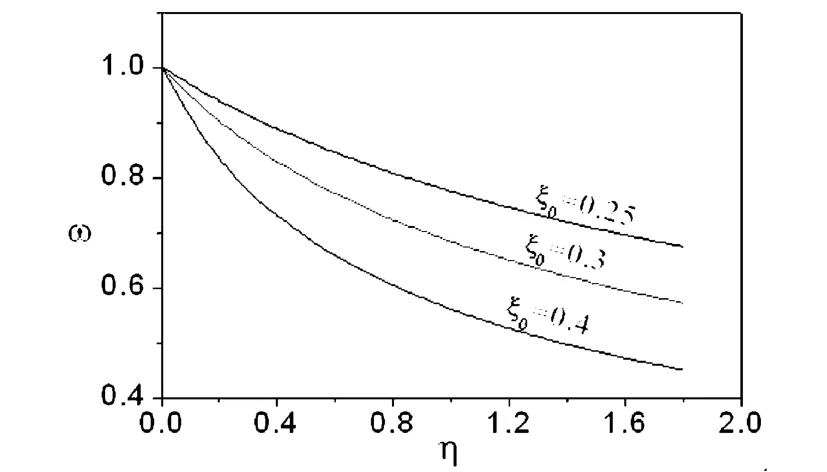
图3 集中质量大小与系统一阶频率关系Fig.3 The relationship between the sizes of the lumped mass and the natural frequency

2.3 集中质量位置对倍周期分叉的影响

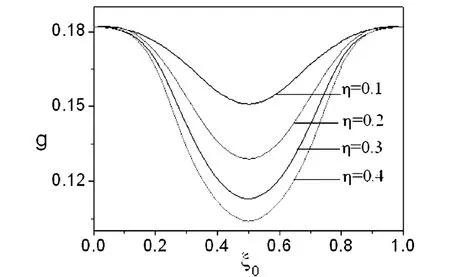
图4 集中质量位置对倍周期分叉的影响Fig.4 The effect of the locations of the lumped mass on period-doubling bifurcation

由于集中质量位置不同，系统的一阶频率和非线性项系数不同，进而导致系统的动力学特性不同.由四阶龙格-库塔法求解后，采用频闪法做庞加莱图，不断调整激励幅值，当庞加莱图上恰好出现两个点时对应的激励幅值即为倍周期分叉解.图4研究了集中质量位置对系统倍周期分叉的影响.其中横轴为集中质量相对梁的位置，纵轴是发生倍周期分叉时的外激励幅值，取μ＝0.2.由图可知，集中质量的位置对倍周期分叉的影响关于ζ0＝0.5对称，且跨中最容易发生倍周期分叉.当ζ0≤0.5时，集中质量越靠近跨中，系统发生倍周期分叉所需的外激励就越小，即倍周期分叉越容易发生；越过跨中后，集中质量越远离跨中，系统发生倍周期分叉所需的外激励就越大，即倍周期分叉越不容易发生.此外，当集中质量离边界较近时（ξ0≤0.1），不同集中质量下的倍周期分叉解相同，说明在此位置下集中质量的大小对系统几乎没有影响，起主导作用的是集中质量的位置；当0.2≤ξ0≤0.9时，同一位置处，集中质量越大，其倍周期分叉解就越小，表明集中质量的大小对系统也有一定的影响.

2.4 集中质量大小对倍周期分叉影响

图5采用和图4相同的方法研究了集中质量大小对系统倍周期分叉的影响.图中横轴是集中质量与梁的质量比值，纵轴为梁发生倍周期分叉时外激励的幅值，取μ＝0.2.由图可知，集中质量越大，发生倍周期分叉所需的外激励就越小，即倍周期分叉越容易发生.当η≤0.9时，曲线变化较快，表明集中质量对倍周期分叉的影响较强；η≥1.2时，曲线变化缓慢，集中质量对倍周期分叉的影响较弱.此外，不难发现，对于同一集中质量，越靠近跨中，倍周期分叉解就越小，表明集中质量的大小和位置对系统相互影响.

图5 集中质量大小对倍周期分叉的影响Fig.5 The effect of the sizes of the lumped mass on period-doubling bifurcation

2.5 主共振下激励幅值对非线性特性的影响

当外激励频率接近该非自治系统的一阶频率时，系统将发生主共振.图6是主共振下，激励幅值g在1.03到2.8之间变化时系统的分叉图.此时η＝0.1，ζ＝0.5，μ＝0.2，ω＝0.8885＝0.8883.由图6可以看出，系统经历了周期-混沌-周期的运动过程.固定上述参数，g＝1.05时，系统做周期运动；增大g到1.124时，系统发生倍周期分叉，做2T周期运动；继续增大激励幅值，当g＝1.312时出现连续频谱，结合相图和庞加莱图可判断此时系统运动为混沌，如图7（a-b）所示；随后，系统在经历了4T周期运动及混沌后，逐渐回归到周期运动.于是，在这一过程中观测到了周期运动-倍周期分叉-混沌运动-周期运动.这充分说明，通过控制激励幅值，可以控制系统倍周期分叉的产生，从而阻止系统由倍周期分叉进入混沌运动.

图6 轴向激励分岔图Fig.6 The bifurcation of axial excitation

图7 g＝1.312时的混沌运动（a）相图；（b）庞加莱图Fig.7 The chaos at g＝1.312，（a）The phase diagram；（b）The Poincare diagram

3 结论

通过对轴向周期激励下一端固定一端夹支，带集中质量的屈曲梁的非线性动力学行为的研究，得到了梁随激励幅值变化的运动规律以及集中质量的大小和位置对系统一阶频率和倍周期分叉的影响.研究表明，随着集中质量的增大，系统的一阶频率和倍周期分叉解会逐渐减小；此外，系统的一阶频率和倍周期分叉解随着集中质量与固定端的距离的增加而减小，并且关于跨中对称，跨中处一阶频率最小，且最容易发生倍周期分叉；随着激励幅值的增大，系统会经历周期-混沌-周期的运动过程，非线性行为非常丰富.因此，在工程结构中可以通过控制集中质量的大小和位置，调节外激励幅值，来改变系统的一阶频率，控制系统倍周期分叉解的产生，阻止由倍周期分叉导致的混沌运动，从而保持系统的稳定性，达到合理设计结构的目的.

1 Tseng W Y，Dugundli J.Nonlinear vibrations of a beam under harmonic excition.ASME.Journal of Applied Mechanics，1971，38（3）：467～476

2 Emam A，Nayfeh A H.On the nonlinear dynamics of a buckled beam subjicted to a primary-resonance excitation.Nonlinear Dynamics，2004，35：1～17

3 Kreider W，Nayfeh A H.Experimental investigation of single-mode responses in a fixed-fixed buckled beam.Nonlinear Dynamics，1998，15：155～177

4 季进臣，陈予恕.参激非线性振子不稳定区域的实验研究.振动工程学报，1997，10：491～495（Ji JC，Chen Y S.The experimental study on the unstable area of the parameter excited nonlinear oscillator.Journal of Engineering Vibration，1997，10：491～495（in Chinese））

5 姚志刚，张萌，张伟.压电复合材料梁的全局分叉、混沌动力学分析.动力学与控制学报，2011，9（3）：207～213（Yao Z G，Zhang M，Zhang W.Global bifurcation and chaotic dynamics of laminated composite piezoelectric beam.Journal of Dynamics and Control，2011，9（3）：207～213（in Chinese））

6 Ozkaya E，Sarigul M，Boyaci H.Nonlinear transverse vibrations of a slightly curved beam carrying a concentrated mass.Acta Mechanica Sinica，2009，26（6）：871～882

7 Satio H，Sato K，Yutani T.Non-linear forced vibrations of a beam carrying concentrated mass under gravity.Journal of Sound and Vibration，1976，46（4）：515～525

8 傅衣铭.结构非线性动力学分析.广州：暨南大学出版社，1997（Fu Y M.The analysis of nonlinear dynamics of structures.Guangzhou：Jinan University Press，1997（in Chinese） ）