一类异构多智能体系统有向图下的广义平均一致性分析

孙一杰 张国良 张胜修

（1.第二炮兵工程大学控制工程系，西安 710025）（2.中国人民解放军96211部队，红河 654300）

引言

近年来，分散式多智能体协同控制系统在无人航天器的协同控制、多机器人编队控制等领域得到了广泛应用，逐渐成为控制理论、统计物理学、生物学、应用数学、计算机科学等学科领域研究的热点问题.到目前为止，研究人员通过采用图论、矩阵论、频域分析方法、李亚普诺夫稳定性理论等方法，对一致性问题进行了研究，获得了许多一阶、二阶以及高阶多智能体系统的一致性标准［1-4］.

以上结论都是基于同构系统，但异构系统在工程实际中广泛存在.基于以上考虑，Liu研究了离散时间有界通信时延下的异构多智能体一致性问题［5］.Kaizuka和Tsumura采用参考自适应控制方法处理了异构多智能体问题［6］.Zheng和Zhu采用图论和李亚普诺夫方法研究了无向拓扑情况下的异构多智能体一致性问题［7］.Tian研究了高阶未知时延的异构多智能体一致性问题［8］.朱亚锟，关新平等研究了异构多智能体系统的有限时间一致性问题［9］.

以上异构系统的研究都是集中解决系统是否一致和收敛速度的问题，对于一个给定的系统往往需要知道最终的收敛值，即控制的最终目标.对于同构系统，现在研究较多的是平均一致性.所谓平均一致性就是所有智能体状态收敛到初始状态的平均值.针对同构系统的平均一致性问题，取得了许多成果［3，10-13］.在此基础上，本文研究了异构多智能体系统的一致性收敛问题.通过采用平均一致性的基本思想，得出了系统收敛到一个给定的最终收敛值的充分条件，并称之为异构系统的广义平均一致性.本文在文献［13］基础上对异构系统的广义平均一致性进行了研究，不同于文献［13］基于辅助变量的协议设计可以直接给出，该异构系统为一阶、二阶模型的混合，个体间状态存在差异，基于参考变量的协议设计较文献［13］困难，本文首先对异构系统提出一般一致性协议，然后对该协议进行拓展，设计基于辅助变量的一致性协议，最后基于图论、非负矩阵理论、特征值扰动等理论进行分析证明，表明该协议使得异构多智能体系统在任意强连通有向图下达到广义平均一致性.该收敛值与采样时间间隔T和系统初始值有关，在采样时间间隔的范围内，通过调整采样时间间隔，可以使系统收敛值在一定范围内变化，使系统收敛到该范围内的任意值.

1 问题描述

1.1 预备知识

一个有向图G＝（v，ε），由顶点集V＝｛1，2，…，n｝，边集ε⊆v×v，eij∈ε表示G中i到j的有向边，表示节点j可以获得节点i的信息.对于每一个节点i∈v，＝｛j∈v：eji∈ε｝表示为入邻居集｛j∈V：eij∈ε｝表示出邻居集并且排除自循环边，即更新权重aij满足，如果j∈否则aij＝0，并且设A为有向图G的邻接矩阵A＝［aij］∈Rn×n，元素为更新权重.拉普拉斯矩阵定义为L＝D-A＝［lij］∈Rn×n，D＝diag是度矩阵.则矩阵I-L（当∑j∈N+iaij＜1）是非负矩阵，并且所有行和为1，I-L是行随机矩阵.设矩阵B＝［bih］∈Rn×n，元素为输出权重.定义矩阵则矩阵E非负矩阵且每一个列和为1，则为列随机矩阵.在有向图G中从节点i1到is是一个边的序列ei1i2，…，eis-1isij∈V.如果图G中存在一个节点使得从这个节点到其它每一个节点都存在一条有向路径则称该图有一个生成树.强连通是指任意节点均存在有向路径到达每一个节点.

对于一个由n个一阶、二阶组成的混合异构系统，假设前m个智能体为二阶，余下n-m个为一阶.二阶智能体入邻居表示为一阶智能体入邻居表示为二阶智能体出邻居表示为一阶智能体出邻居表示为.则拉普拉斯矩阵可以表示为，

Ls表示m个二阶智能体之间的拉普拉斯矩阵，Lf为n-m个一阶智能体之间的拉普拉斯矩阵.Asf表示二阶个体与一阶个体的邻接关系，Afs表示一阶个体与二阶个体的邻接关系.

几个重要矩阵的定义：

非负矩阵：矩阵所有的元素都非负.随机矩阵：矩阵所有行和为1的非负矩阵.SIA矩阵：如果随机矩阵P满足limk→∞Pk＝1vT则称该矩阵是SIA矩阵.

1.2 异构多智能体系统

假设异构多智能体系统由一阶和二阶智能体组成，前m（m＜n）个智能体为二阶，余下的（nm）个智能体为一阶.该异构系统模型描述如下：

采用如下离散时间协议：

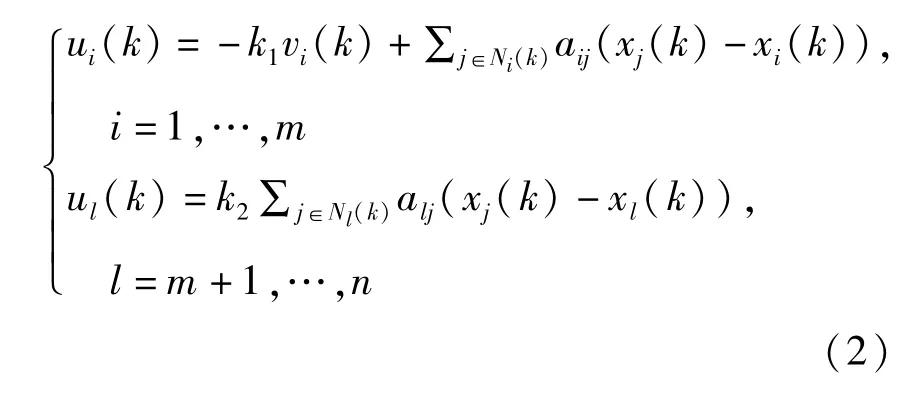
定义zi（k）＝xi（k）+Tvi（k），i＝1，…，m，则该异构系统可以描述为：

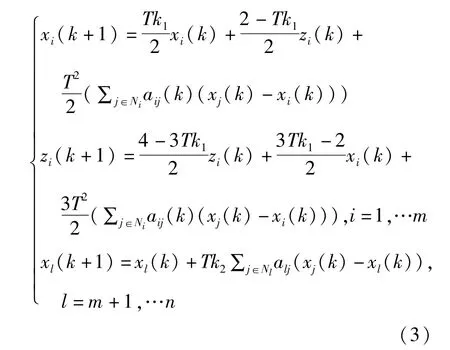
（1）～（3）中，k1＞0，k2＞0为控制增益，0＜T＜Tmax为采样时间间隔，下文将给出取值范围.令y（k）＝＝［x1，…，x］T，m［xm+1，…，xn］T.则系统（3）可以描述为：

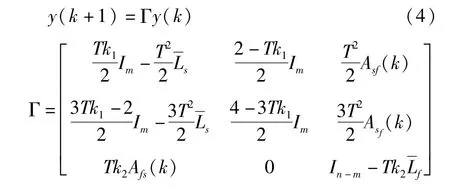
注1：协议（2）为静态一致性协议，引入的状态变量zi（k）＝xi（k）+Tvi（k），i＝1，…，m，可以看出，当系统（3）获得一致性时，达到了协议（2）的控制目标.

下面给出广义平均一致性的定义：

定义1对于系统（1），当且仅当：

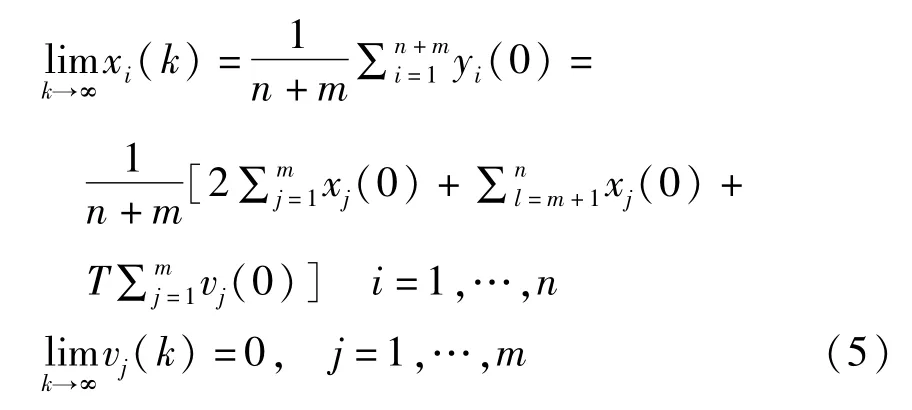
则称所提出的一致性协议使异构系统达到了广义平均一致性.

可以看出系统（4）获得平均一致性时，系统（1）获得广义平均一致性.

1.3 有向图下广义平均一致性问题分析

在时间k（k为非负整数），系统状态可以描述为：

根据上文给出的异构系统广义平均一致性定义，可以得出广义平均一致性的目标就是设计分布式协议，使得有向图G中的每一个节点通过与邻居信息交互进行信息更新，使得每一个yi（k）最终收敛到初始状态的平均值ya＝1Ty（0）/（n+m）.在一般强连通有向图中要实现平均一致性，主要的困难的是系统状态和1Ty（k）是变化的，导致了对初始状态平均值跟踪的失败.针对这个问题，引入一个变量si（k）∈R，称为辅助变量.记s（k）＝［s1（k），…，sn+m（k）］T＝［ss，sz，sf］T∈Rn+m且s（0）＝0.辅助变量的功能是记录状态的变化，使得对于所有时刻k，1T（y（k）+s（k））＝1Ty（0），保持1T（y（k）+s（k））是恒定的.

定义2对于每一个初始条件（y（0），0），当k→∞时，（y（k），s（k））→（ya1，0），则称异构多智能体系统达到了广义平均一致性.

2 一般强连通有向图下的广义平均一致性分析

本部分，首先提出基于辅助变量的线性分布式协议，主要是对上文异构系统一致性协议的一种拓展.然后对所提出的协议进行证明，确保在任意强连通有向图下该异构系统实现广义平均一致性.

2.1 基于辅助变量的协议描述

在系统（3）的基础上，借鉴文献［13］的设计思路对系统中的一阶智能体和二阶智能体对状态和辅助变量做如下更新：

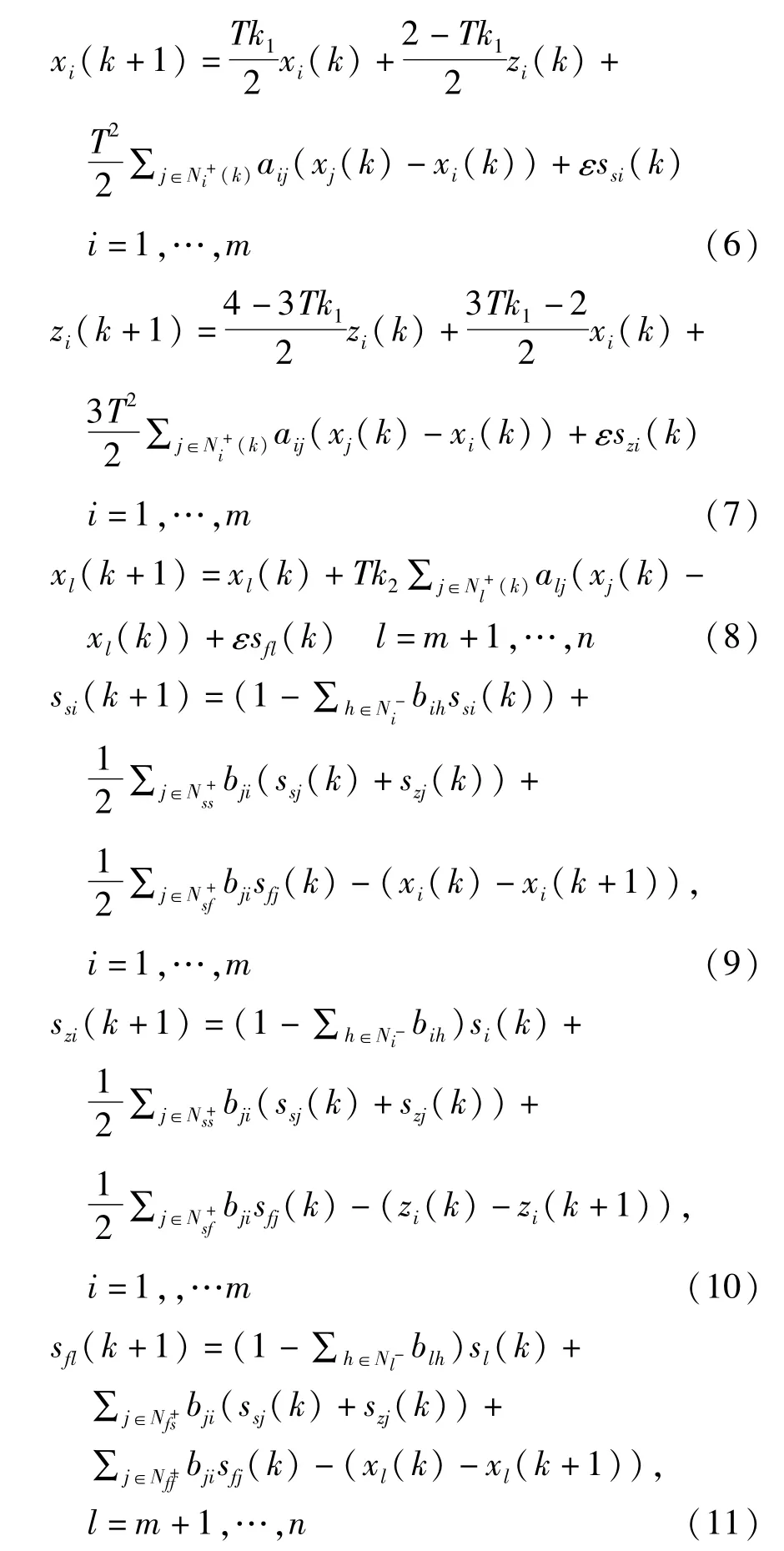
ε＞0为干扰系数.通过以上分析可以将（6）～（11）用矩阵的形式进行表示：

其中

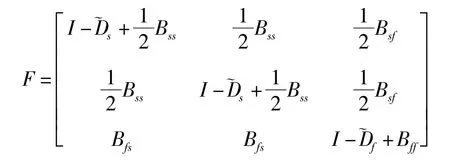
容易验证F和Λ均为列随机矩阵.

2.2 收敛性分析

本部分采用非负矩阵理论和矩阵扰动理论分析出实现广义平均一致性的条件.

引理1当通信拓扑图G为强连通时，矩阵Γ为随机矩阵且仅有一个1特征值，非1特征值的模均小于1的条件是采样时间T及控制参数k1，k2满足：

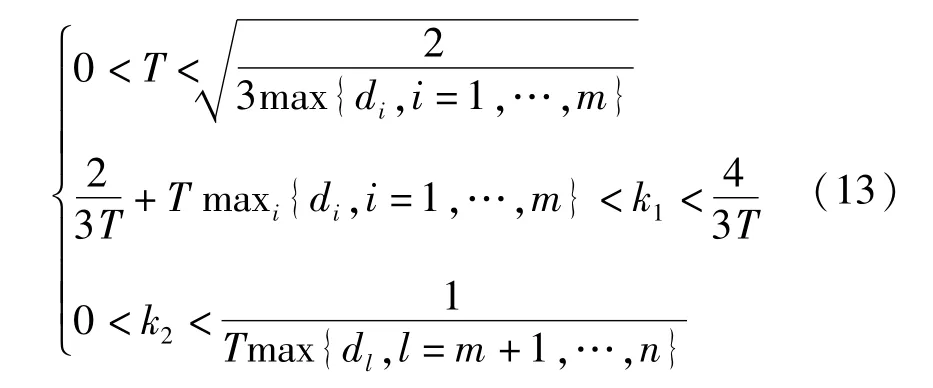
其中，di，i＝1，…，n为系统度矩阵的对角元素.

证明：当满足（13）可以得出矩阵Γ满足以上条件时为非负矩阵，容易验证该矩阵行和为1，所以矩阵 Γ为随机矩阵.又对做初等行列变换可得：

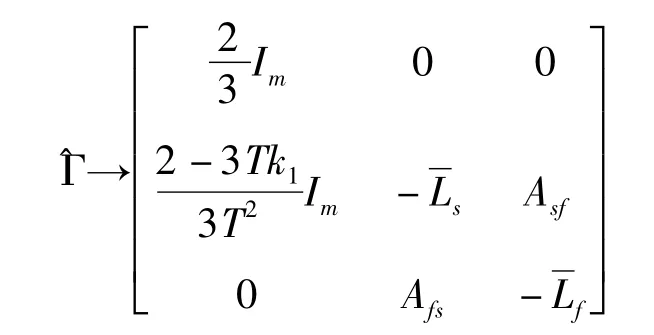
则可以得出rank（＾Γ）＝m+rank（L），又强连通有向图中，rank（L）＝n-1.设做行列变换可以验证rank）＝n+m，则矩阵Γ不含-1特征值.根据随机矩阵属性λ＝1是矩阵Γ代数重复度为1的一个特征值，并且其余特征值的模都是小于1的

定理1系统（12）实现广义平均一致性的充分条件是矩阵Λ仅有一个1特征值，并且非1征值的模均小于1.

证明：当矩阵Λ仅有一个1特征值，并且其它特征值模数小于1时，可以将Λ写为Jordan规范型，具有如下形式：

又非1特征值模数均小于1，则

不失一般性，选择可以验证w1为Λ阵1特征值对应的特征向量.又Λ是列随机矩阵，则为1特征值对应的左特征向量.又有得α＝1/n+m.则

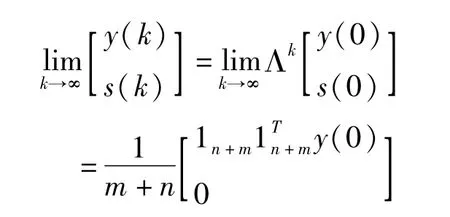
即则系统（12）实现广义平均一致性.

引理2［14］一个n×n的矩阵W（ε），随实数 ε≥0光滑变化.取l∈［1，n］；设 λ1＝λ2＝… ＝λl为矩阵W（0）的单一特征值，并且具有线性独立的右特征向量y1＝y2＝…＝yl，和线性独立的左特征向量z1＝z2＝… ＝zl，使得：

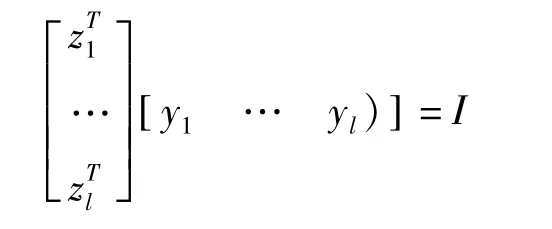
取比较小的 ε＞0，λi（ε）表示 λi，i∈［1，l］相应的W（ε）的特征值.则导数dλi（ε）/dε｜ε＝0存在，并且该导数值是以下l×l矩阵对应的特征值：

引理3［16］（Perron-Frobenius）如果矩阵A是不可约的，则谱半径ρ（A）＞0为矩阵单一特征值，且对应特征向量是正的.

定理2系统（12）满足（13）式时达到广义平均一致性的充分条件是参数ε足够小且有向图G为强连通.

证明：设则Λ＝Λ0+εH，矩阵 Λ通过矩阵 Λ0通过 εH“扰动”获得.矩阵Λ光滑的依赖于ε.可以看出矩阵Λ0是分块下三角矩阵，其谱属性满足σ（Λ0）＝σ（Γ）∪σ（F）.由引理1当通信拓扑图G为强连通时，矩阵Γ与F均仅有一个1特征值，几何重复度与代数重复度均为1，且非1特征值的模均小于1.表明又rank（Λ0-I）＝2（n+m）-2，则 Λ0特征值1的代数重复度和几何重复度均为1.在一个小的扰动εF下，Λ0的特征值 λ1＝λ2＝1发生了变化.根据引理2计算导数dλ1（ε）/dε，dλ2（ε）/dε，λ1（ε），λ2（ε）为 Λ与 λ1，λ2相关特征值.对于矩阵 Λ0的特征值1，有线性无关的右特征向量和线性无关的左特征向量z1＝［1T，为矩阵F特征值 ρ（F）对应的左特征向量，1Tv1＝1，v2为 ρ（Γ）对应的右特征向量.满足通信拓扑强连通，可以看出矩阵F和Γ均为不可约矩阵，则根据引理3可知v1和v2均为正的特征向量.根据引理2可得

对于较小的 ε，导数dλ1（ε）/dε，dλ2（ε）/dε存在，且为矩阵I的特征值.则dλ1（ε）/dε＝0，dλ2表明当 ε足够小的时，λ1（ε）保持不变，λ2（ε）沿实轴向左移动，则必然存在正整数 δ1使得，λ1（δ1）＝1，λ2（δ1）＜1.另一方面特征值是矩阵元素的连续函数，则必定存在正的δ2，使得这样对于任意足够小的 ε∈（0，min｛δ1，δ2｝），矩阵 Λ有一个单一特征值1，且非1特征值的模均小于1.因此根据定理1，系统广义平均一致性可达.

3 统收敛值分析

通过以上分析得出了系统实现广义平均一致性的充分条件.得出的最终收敛值为：

令

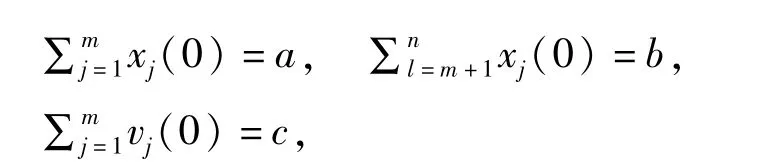
当c＞0时为：

当c＜0时，

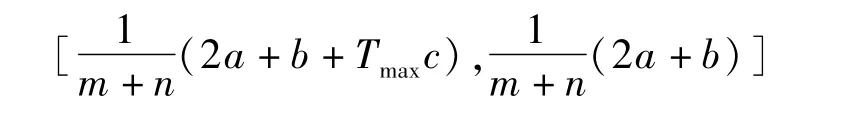
引理1给出了采样时间间隔T的取值范围，这样根据系统的初始状态就可以确定出系统的收敛区间，结合实际需求，就可以通过调整采样时间间隔对系统最终的收敛值进行调整.

4 仿真验证

本部分主要对本文获得的理论结果进行仿真验证.通过采用所得出的结论，实现异构多机器人系统的聚集控制.考虑一个4个机器人组成的多机器人系统，通信拓扑如图1所示，其中，节点1，2为二阶模型，节点3，4，为一阶模型，显然通信拓扑强连通.机器人Ri的位置为xi＝［xix，xiy，θi］T，i＝1，2，3，4，5，二阶机器人的速度表示v＝［vix，viy，ωi］T，i＝1，2，3，其中xix，xiy，θi表示机器人x，y方向上的位移和方向角，vix，viy，ωi为二阶个体x，y方向上的速度和转动速度.

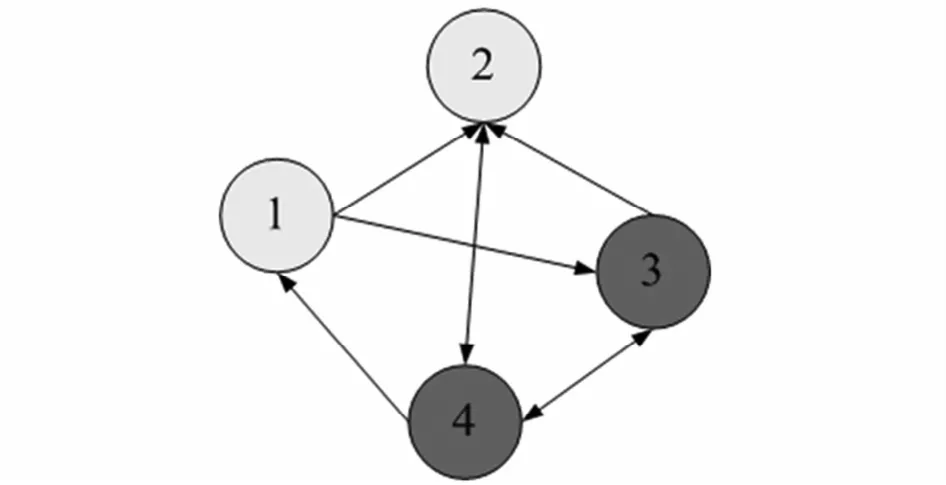
图1 信息交互拓扑图Fig.1 The information interaction graph of themulti-agent

aij＝1/（任意选取x1（0）＝［1，2，1］T，x2（0）＝［1，-1，2］T，x3（0）＝［1，2，-1］T，x4（0）＝［1.5，2，-1］T，v1（0）＝［0.5，1，0.5］T，v2（0）＝［-1，-1，1.2］T，仿真结果如图2，图3，图4所示.

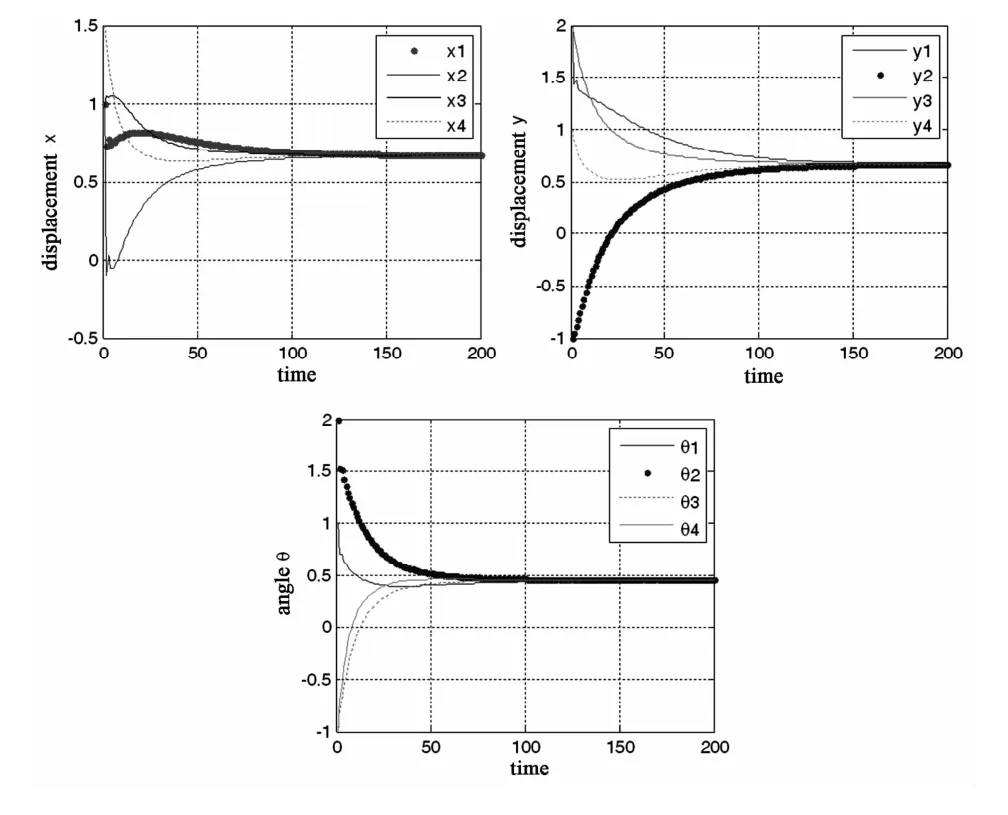
图2 机器人的位置信息Fig.2 The positions of robots

图2显示了智能体的位置状态信息的，根据（5）计算出系统在三个变量上的广义平均一致性分别为可以看出系统实现了广义平均一致性.图3显示了二阶智能体的速度状态信息，可以看出所有二阶智能体的速度一致趋于0.图3显示了辅助变量的变化情况，可以看出在系统达到广义平均一致性的过程中所有辅助变量一致趋于0，与理论分析结果一致.

图3 二阶机器人速度信息Fig.3 Thevelocities of second-order robots

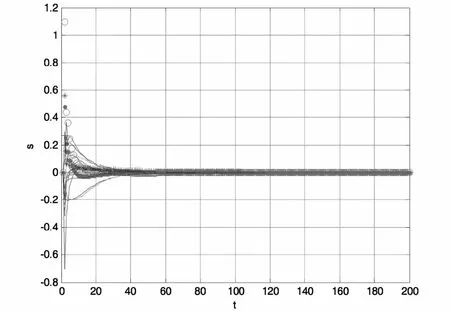
图4 辅助变量信息Fig.4 Theadditional variable information

5 结论

本文对包含一阶、二阶混合的离散时间异构多智能体系统的一致性进行研究，提出了该类异构智能体系统的广义平均一致性概念.在此基础上，采用同构系统平均一致性研究的方法，针对先前文献要求网络具有平衡结构的问题，提出了一种新的分布式协议，在任意强连通交互拓扑下，实现了异构多智能体的广义平均一致性.根据收敛值的性质，得出了收敛值的范围.最后对该结果进行了仿真验证，结果与理论分析一致.该研究主要是在固定拓扑情况下，下一步研究考虑将现有的理论结果拓展到动态拓扑的情况中.

1 Vicsek T，Czirok A，Jacob E B.，Cohen I，Schochet O.Novel typeof phase transition in a system of self-driven particles.Physical Review Letters，1995，75（6）：1226～1229

2 颜青，马米花，吴海亮.具有引导者的多智能体网络系统的脉冲一致性.动力学与控制学报，2012，10（2）：152～156（Yan Q，Ma，M H，Wu H L.Impulsive consensus of networked multi-agentsystem with a leader.Journal of Dynamics and Control，2012，10（2）：152～156（in Chinese））

3 Olfati-Saber R，Murray R M.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control，2004，49（9）：1520～1533

4 Ren W，Beard RW.Consensus seeking inmulti-agentsystems under dynamically changing interaction topologies.IEEE Transactions on Automatic Control，2005，50（5）：655～661

5 Liu C L，Liu F.Stationary consensus of heterogeneous multi-agent systems with bounded communication delays.Automatica，2011，47：2130～2133

6 Okajima T，Tsumura K，Hayakawa T，Ishii H.Adaptive consensus of discrete-time heterogeneous multi-agent systems.In：SICE Annual Conference，2011：2237～2242

7 Zheng Y，Zhu Y，Wang L.Consensus of heterogeneous multi-agent systems.IET Control Theory and Applications，2011，5（16）：1881～1888

8 Tian Y P，Zhang Y.High-order consensus of heterogeneous multi-agent systems with unknown communication delays.Automatica，2012，48：1205～1212

9 Zhu Y K，Guan X P，Luo X Y.Finite-time consensus of heterogeneous multi-agent systems.Chinese Physics B，2013，22（3）：038901

10 Kingston D B，Beard RW.Discrete-time average-consensus under switching network topologies.In：Proceedings of the 2006 American Control Conference Minneapolis，2006：3551～3556

11 Sun Y G，Wang L，Xie G.Average consensus in net-works of dynamic agents with switching topologies and multiple time varying delays.System＆Control Letters，2008，58：175～83

12 Shuai L，Tao L，Lihua X.Distributed consensus for multi-agent systemswith communication delays and limited data rate.SIAM Journal on Control and Optimization.2011，49（6）：2239～62

13 Cai K，Ishii H.Average consensus on general strongly connected digraphs.Automatica，2012，48：2750～2761

14 Seyranian A P，Mailybaev A A.Multi-parameter stability theory with mechanical applications.Singapore：World Scientific，2004

15 Lin Z Y，Francis B，Manfredi M.Necessary and sufficient graphical conditions for formation control of unicycles.IEEE Transactions on Automatic Control，2005，50（1）：121～128

16 Horn R A，Johnson CR.Matrix analysis.London：Cambridge：Cambridge University Press，1985