以“五知”为导向的五年制高职数学教学设计

陆静

摘要：以“五知”为导向的五年制高职数学教学设计主要依据五年制高职数学课程的特征与学生的已知、未知、能知、想知、怎知的学情，从教学理念、教学环节、教学媒体、教学形式、教学活动、教学方法和教学模式几方面科学预设偶函数教学。该教学设计思路清晰，可取得预想教学效果。

关键词：“五知”;五年制高职数学;教学设计

中图分类号：G712 文献标志码：A 文章编号：1673-9094-C-（2015）05-0022-03

五年制高职数学教学就是要依据该课程的特征，以学生的“五知”——已知、未知、能知、想知、怎知五方面为导向读懂学生的学习需要，科学合理地设计教学过程。具体而言，“已知”指学生已经具备的相关知识基础和学习新知的生活经验等;“未知”指本节课学生将要学习的知识与技能，以及各种学习能力;“能知”指学生凭借已有知识、能力和经验，可以自主获取的知识;“想知”指学生希望了解的知识及获取过程。“怎知”指学生用怎样的思维方式和学习方法参与数学学习活动并实现学习目标。

一、以“五知”为导向的教学理念

五年制高职艺术设计专业的学生形象直观思维较强，逻辑抽象思维较弱，通过“五知”学情分析可知：关于偶函数概念的学习，他们已知轴对称图形定义，未知偶函数定义及判断方法，能知生活中丰富多样的轴对称图形，想知什么样的函数是偶函数、偶函数有何特征、如何判断偶函数。如何引导学生从“已知”迈向“未知”成为本节课设计的关键。

荷兰数学教育家弗赖登塔尔认为，数学来源于现实，存在于现实，并且应用于现实，而且每个学生有各自不同的“数学现实”[1]。由此说明数学来源于生活，存在于现实，并且应用于生活，教学过程就是要帮助学生把现实生活问题转化为数学问题的过程。基于此，本节课的教学理念为“数学教学的生活化”。

二、以“五知”为导向的教学环节确定

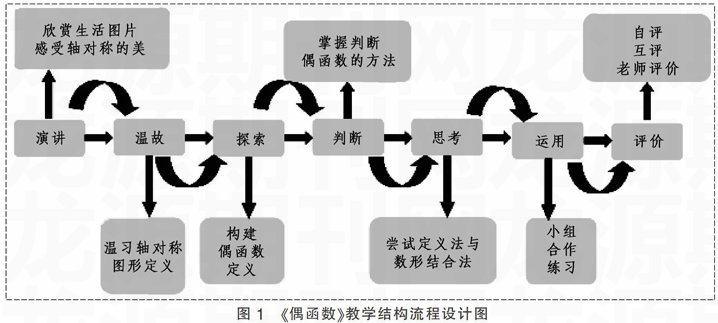
教学环节是指学习活动内容各部分之间的排列次序，是对“先教什么”、“后教什么”作出合理、科学的安排。为了激发学生的智慧潜能，培养学生的内在学习动机，依据学生的“五知”学情与本节课知识内容的特征，笔者确立了“演讲、温故、探索、判断、思考、运用、评价”七个环节（如图1）。

三、以“五知”为导向的教学媒体运用

所谓教学媒体，就是教学过程中传递和存储知识信息的载体或工具。由于学生是依靠感官来接受知识信息的，媒体运用是否恰当势必影响到教学质量，所以恰当运用教学媒体也是教学设计的一个重要问题。教学媒体种类丰富，但可归纳为视觉媒体，如图书、图片、黑板报等;听觉媒体，如音乐、音频等;视听媒体，如视频、带解说的动画、活动影像等。

如在“演讲”环节，笔者依据学生的“已知”、“能知”的情况，首先指导学生课前搜集生活中轴对称图形的图片——具有轴对称性的建筑图片、汽车标志图案，传统工艺品如剪纸作品等，然后编写主题为《体验生活中轴对称图形的美》的演讲稿，在课堂的前三分钟开展演讲，采用视觉媒体“图片”与听觉媒体“学生代表演讲”相结合的视听媒体方式展示。如此设计不仅激发了学生的学习兴趣，而且验证了教师预设的学生“能知”对于学生参与自主学习的重要意义，为学生的“已知”与“未知”之间搭建了一座桥梁。

又如在“判断”环节，设计一组例题：请判断f（x）=2x2、h（x）=x、g（x）=x4+1三个函数中哪些是偶函数？笔者考虑到学生的“想知”，即想通过信息化的手段获取函数的图像，引导学生在几何画板软件中画出三个函数的图像，采用视听媒体让学生观察函数生成的动画，感官获得三个函数的信息：函数f（x）=2x2与g（x）=x4+1的图像关于y轴对称，而函数h（x）=x图像不关于y轴对称，这样的认知过程更直观，更全面、生动。

四、以“五知”为导向的教学形式选用

教学形式就是关于教学活动应该怎样组织，教学时间和空间应该怎样加以控制和利用所采用的形式。选择恰当的教学形式能提高课堂教学与学习的效率。教学形式具有多样化，主要有班级学习、小组合作学习、“个别”学习等形式。

数学课堂学习要给学生足够的时间练习，让学生在“做”中“学”，收获“做”的体验，如在运用环节，依据学生“已知”判断偶函数的方法，可采用小组合作学习的形式，设计分组分层练习内容：判断下列函数是不是偶函数？说说你是怎样判断的？A组：（1）f（x）=2x+1，（2）f（x）=x4+2x2;B组：（1）f（x）=x3+x2，（2）f（x）=■;C组：（1）f（x）=■，（2）f（x）=x2+x+1。学生在分组学习、合作交流、竞争解题中互帮互助，在练习中逐步掌握了判断偶函数的两种方法，形成了“心中有图就有解”的数学学习意识。

五、以“五知”为导向的教学活动组织

数学课堂教学活动一般包括复习引导、讲解新课、巩固新知、课堂小结、布置作业等，这样的数学教学方式最大的不足就是以教师为中心，忽视学生学习主体的地位，学生学习数学的过程实际上成了“做数学”的过程。弗赖登塔尔在《作为教育任务的数学》一书中提出了“教学法的颠倒”，即“你不应该把你的数学成果按照你发现它的那种过程去向别人讲解，而要采取另一种方式，即设想你当时已经有了现在的知识，你将是怎样发现那些成果的;或者设想一个学生的学习过程得到指导时，他是应该怎样发现它的。”[2]据此，在偶函数教与学的过程中，笔者在每个环节都关注学生的思维实验，即帮助学生把他要学的知识“再创造”出来。

如在“探索”环节，由于学生对轴对称图形已经有了充分的感性与理性认识，他们“想知”什么是偶函数，于是在预设好的学习情境中，学生开始主动观察二次函数的图像y=x2，并积极思考以下问题：（1）这条抛物线的对称轴是哪条直线？（2）（1，1），（2，4），（3，9），（4，16）四个点关于y轴对称的点的坐标分别是什么？（3）这是具体的特殊的点，那么对于任意的点A（x0，f（x0））在函数y=x2的图象上，其关于y轴对称的点A（-x0，f（x0））也在函数y=x2的图象上吗？（4）用垂直于y轴的直线截抛物线，你有什么发现？（5）被截取的函数图像，被y轴分为对等的两段，那么构成这两段图像的点是否成对出现？⑹对称轴两侧对应点的坐标有什么关系？

学生在上述6个具有关联性的问题引导下自主探究理解偶函数。抽象的函数概念让学生很有陌生感，而具体的函数实例让学生具有亲切感。掌握抽象数学概念的最佳办法就是从具有代表性的实例出发，所以笔者从学生的“想知”和“能知”入手，以具体特殊函数为脚手架，逐步引导学生投入观察、思考、探索、互动的学习过程中，主动建构偶函数的概念，指导学生寻找到掌握理解偶函数概念的最佳途径。再者，从学生持续学习能力增长的角度着眼，引导学生在有关函数知识学习的过程中，铭记“心中有图就有解”这一理念的战略意义。

六、以“五知”为导向的教学方法选择

由于教学方法的设计与使用效果受到教学内容、学生水平以及教师本人经验等影响与制约，并不存在某种所有教师可以直接套用的教学方法，即“教无定法”。然而，在数学课堂教学中常用的教学方法有讲解法、谈话法、发现法等。

如果说“演讲”环节是从感性的一面帮助学生回忆初中时所学的轴对称图形，即从视觉与听觉效果上引导学生感知生活中的轴对称图形，解决了学生的“怎知”困惑，那么“温故”这个环节正是在了解学生“已知”轴对称图形特征的前提下，师生共同经历着类似于苏格拉底式的教学互动，引导学生理性重温轴对称图形概念，为下一环节学习偶函数的概念做好预设。在这两个环节中，笔者均采用了谈话法，即将教学内容设计成系列问题，然后在课堂上据此问题与学生开展对话，引导学生积极思考，自己去探索问题、解决问题，获得知识，并用自己的语言表述出来的方法。

七、以“五知”为导向的教学模式建构

对于偶函数的教与学，笔者采用了“探究式教学模式”。著名的实用主义教育家杜威提出了以儿童为中心、从“做”中“学”的主张。杜威认为科学教育不仅仅是让学生记忆百科全书式的知识、也是一种过程和方法。本节课，笔者在“演讲”环节营造了《体验生活中轴对称图形的美》的演讲这一情境，激发了学生学习热情与思考，为学生探究偶函数的概念预设了生活实例;在“探索”环节设计了具有一定难度坡度的问题，启发引导学生发现解决;在“思考”环节设计了数学问题，引导学生探究问题的同时，注意尝试用多种方法解决问题，让学生时时刻刻处于探究中学习，收到了很好的教学效果。

我们写文章时需要有一条清晰的思路，如果把每个环节看成“珠子”的话，那么这些“珠子”需要用一根线将它们串连起来。五年制高职数学课堂教学设计也需要一根清晰的线，即以学生的“五知”——已知、未知、能知、想知、怎知为导向，安排教学环节，选用教学媒体，开展教学活动。

参考文献：

[1][2]【荷】弗赖登塔尔.作为教育任务的数学[M].陈昌平，译.上海：上海教育出版社，1995.

（责任编辑：张志刚）

The Teaching Design of Five-year Higher Vocational Math

Guided by the "Five Knows"： A Case Study

LU Jing

（Jiangsu Yangzhou Higher Vocational College of Business， Yangzhou 225127， Jiangsu Province）

Abstract： The teaching design of five-year higher vocational math guided by the "five knows" is to design the even function teaching from teaching concept， steps， media， form， activities， methods and mode based on the characteristics of five-year higher vocational math curriculum and the students' situation of known， unknown， be able to know， want to know and how to know. This teaching design has clear ideas and can obtain expected teaching effects.

Key words： the "five knows"; five-year higher vocational math; teaching design