基于经验模态分解与支持向量机的道路交通状态预测
邓 捷,郭桂林
(1.贵州交通职业技术学院,贵州 贵阳550008;2.重庆交通大学,重庆 400074)
伴随城市的快速发展,汽车数量逐年增加,交通拥堵问题已严重影响了人们的生活质量。智能交通被认为是解决交通问题的最有效方法,而交通控制及诱导是智能交通的核心部分,交通状态短时预测是交通控制及诱导的基础,精确地掌握交通状态信息能为交通管理部门制定出更加科学、合理的交通控制诱导方案。目前,交通状态短时预测方法主要有Kalman滤波、神经网络法、小波分析、动态交通分配及交通模拟法等。城市交通系统是一个非线性、时变的复杂大系统,具有很强的随机性。传统交通状态预测通常采用交通流三参数(速度、密度、流量)进行预测,车流速度能直观地反映出当时的道路交通状态,因此,本文通过对车流速度进行预测来判断交通状态。近年来,小波分析在信号处理上有了广泛的应用,在处理非线性问题时,由于在小波母函数及分解层数的选择上没有完善的理论支撑,克服了人为选取的局限性。经验模态分解(Empirical Mode Decomposition,EMD)则能很好地避免因人为因素而造成的巨大误差。张小蓟将舰船噪声信号分解,刘小峰将原始信号进行经验模态分解,然后利用小波包对出现模态混叠的分量进行再次分解,唐衍将EMD与ARMA结合,建立电力负荷短期预测模型,杨柳青将EMD与SVM相结合对航空客流量进行预测。支持向量机(Support Vector Machine,SVM)以结构风险最小化原则为基础,提高算法的泛化能力。因此,本文利用支持向量机分别对EMD分解的各分量进行预测。然后,根据预测结果误差的大小确定各预测分量的权重,最后,将各预测分量融合得到最终预测结果。通过仿真验证,本文提出的模型能很好地预测出道路交通的状态,具有较高的精度。
1 理论基础
1.1 经验模态分解
经验模态分解实际上就是对原信号做平稳化处理的过程。在分解时,EMD能根据数据本身选择合适的基函数,因此,它对数据类型没有严格的要求,非常适合非线性和非平稳信号的分析。分解后得到一组频率由高到低的本征模态分量,并且在分解的过程中不会对原信号有任何的丢失,保证了原信号的完整性。
经验模态分解的基本思想是:找出数据序列的所有极值点,用三次样条函数分别拟合出数据的上下包络线,从原序列中减去上下包络的均值,得到一个去掉低频的新数据序列,对新序列继续上述过程,直到所得到序列满足IMF的条件。其中IMF满足条件:
1)在整个信号长度上,极值点的个数和过零点个数相同或最多相差一个;
2)在任何时间点上,由局部极大值包络线和局部极小值包络线所定义的均值包络线必须为零。
EMD的分解流程如下:
Step1:求出待测信号x(t)的所有极值(极大值和极小值),利用三次样条插值法拟合所有极值,得到原信号的上包络线vmax(t)和下包络线vmin(t)。
Step2:由上下包络线得到均值包络线m1(t),并计算其与原信号的差值。
Step3:判断h1(t)是否满足IMF的两个条件,若满足,则h1(t)为第一个IMF分量;若不满足,则重复Step1、Step2,直至h1(t)满足条件为止,并记下此时的c1(t)=h1(t)。
Step4:将r1(t)=x(t)-c1(t)作为新的序列,重复以上步骤,直至r(t)变成常数或单调函数,不能再分解出IMF分量为止。因为分解中没有信号丢失,则原信号可以表示为
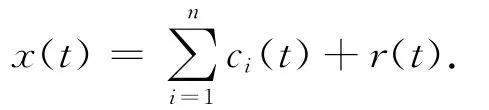
1.2 支持向量机
支持向量机是以统计学理论为基础的数据挖掘方法,能很好地解决小样本、非线性、维度的问题,在数据分类、模式识别及预测方面有广泛应用。
设数据训练集为{xn,yn},其中X为输入,y为输出,则SVM模型可以表示为
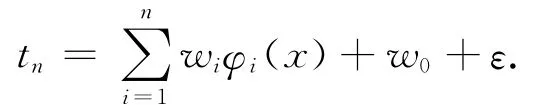
式中:w为权参向量,ε为高斯噪声信号,φi(x)为非线性基函数。
2 基于EMD与SVM的交通状态预测模型
城市路网车流速度能直观地反映出此时路网的交通状态。然而,车速受到驾驶员的主观感受及周边环境的影响,具有较强的随机性。因此,车速数据是一组非线性、实变、非平稳的时间序列。
虽然速度具有较高的随机性,但它还会受到先前道路交通条件及上下游交通的影响,只有综合考虑时间维度和空间维度才能准确预测出此时的道路交通状态。为此,在用SVM预测速度时可以组合两种模式、四种情况:
第一,基于单维参数预测:设当前时刻为t,则vk(t-1)→vk(t);通过上游路段预测待测路段,即vk+1(t)→vk(t);通过下游路段预测待测路段,即vk-1(t)→vk(t)。
第二,基于时空参数预测:综合考虑时间维度和空间维度对路段车速的影响,即vk±1(t-1)→vk(t)。
本文利用EMD-SVM预测模型,其流程如下:
1)将原始数据进行EMD分解,得到一组IMF和一个余量。由于EMD在分解时会在边界出现模态混叠,会对后面的时间序列产生较大影响。因此,为避免模态混叠的影响,将本征模态分量的前面20个数据剔除,将剩下的数据作为各尺度的IMF。
2)为加快训练速度,对各层IMF及余量进行归一化处理,即
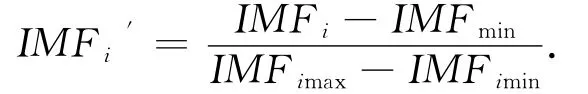
3)利用SVM对各层IMFi′分别进行预测,得到预测结果mi,并将其进行反归一化,得到Mi。
4)计算各层的预测误差,即ERRi=|IMFi-Mi|,将其归一化得

5)将各层的预测结果融合,得到最终的预测结果,即

则

3 案例分析
本文以重庆市出租车GPS数据为例,选取陈家坪立交—科园六路、科园六路—大公馆立交、大公馆立—谢家湾立交三段道路的数据进行分析。其路网结构如图1所示。

图1 路网信息
综合考虑时空参数的影响,选取待测路段2014-12-15~2014-12-19(工作日)一周的 GPS数据为基础,数据以5min为间隔,一天24h共287个数据。先对原数据进行预处理,修正问题数据。
由于篇幅有限,本文只以科园六路—大公馆立交2014-12-19的GPS数据为例,对该组数据进行EMD分解,得到一组本征模态分量和一个余量,如图2所示。

图2 速度EMD分解
由图2可知,EMD分解将速度数据分解成6个IMF分量和一个余量,它们的频率由高到低依次排列,这样既能了解速度波动的细节,又能掌握速度变化的趋势。使速度波动平稳化,将各个频率的波动分解到各尺度上,即将它们隔离开,减小对预测结果的干扰。
同理,可将待测路段(科园六路—大公馆立交)的上下游及前面几个时刻的车流速度进行EMD分解,得到IMF分量和余量。然后,分别对各IMF分量和余量进行SVM建模预测。利用遗传算法对SVM模型参数c和γ进行优化,得到各层的本征模态分量,然后融合、重组,得到最终的预测结果。
由表1可知,MSE表示均方差误差,值越小则预测精度越高。平方相关系数表示预测值和实际值的拟合程度,值越接近1则拟合效果就越好(见图3)。根据时间维度预测误差最大,虽然道路车流速度在时间上具有一定的时间延续性和周期性,但前几个时刻对待测时刻的影响有很大的局限性,其影响能力有限;根据空间维度上的预测,以下游车流速度预测效果较好。由于下游车流速度与待测路段车流速度关联性较强,道路上的车辆都是跟驰行驶,后方车辆速度都要跟随前方车辆速度的变化而进行相应的调整,若下游车流发生交通拥堵,待测路段的车流速度也会随之下降,甚至发生交通拥堵。相反,若下游车流速度畅通无阻,则待测路段车流速度也会随之提高。而综合考虑时空因素(待测路段先前车流速度和下游车流速度)来预测,得到的结果更准确。

表1 预测结果

图3 误差对比
4 结束语
本文在道路交通状态预测中,先利用EMD将车流速度分解成6个IMF和一个余量,将非平稳的速度数据平稳化,减小对预测误差的影响。然后,在各尺度的IMF分量上构建SVM预测模型,最后将预测结果融合得到最终结果。案例分析表明:基于多维时空参数的预测结果要明显优于单维参数预测。而且,基于空间维度的预测结果要优于基于时间维度的预测结果;以下游车流速度预测也要比以上游车流速度预测更加准确;而且,经验模态分解和支持向量机的组合预测也比单一的支持向量机预测模型的精度更高。
[1] 姚智胜,邵春福,高永亮.基于支持向量回归机的交通状态短时预测方法研究[J].北京交通大学学报,2006,30(3):19-22.
[2] 杨露,沈怀荣.希尔伯特-黄变换与小波变换在故障特征提取中的对比研究[J].兵工学报,2009,30(5):628-632.
[3] 张小蓟,张歆,孙进才.基于经验模态分解的目标特征提取与选择[J].西北工业大学学报,2006,24(4):453-456.
[4] 刘小峰,秦树人,柏林.基于小波包的经验模态分解法的研究及应用[J].中国机械工程,2007,18(10):1201-1204.
[5] 唐衍.基于EMD方法的电力系统短期负荷预测[D].上海:上海交通大学,2011.
[6] 杨柳青.基于EEMD的航空客流需求预测技术及其应用研究[D].武汉:华中科技大学,2009.
[7] 邓捷,陆百川,马庆禄,等.基于小波和RBF神经网络的多传感器时间对准算法研究[J].交通科技与经济,2014,16(1):36-39.
[8] 李琦.基于多源数据的交通状态监测与预测方法研究[D].长春:吉林大学,2013.
[9] 马毅林.基于非参数回归的路网短时交通状态预测[D].北京:北京交通大学,2008.

