A Survey of Evolutionary Algorithms for Multi-Objective Optimization Problems With Irregular Pareto Fronts

Yicun Hua, Qiqi Liu, Kuangrong Hao, and Yaochu Jin, Fellow, IEEE

Abstract—Evolutionary algorithms have been shown to be very successful in solving multi-objective optimization problems(MOPs). However, their performance often deteriorates when solving MOPs with irregular Pareto fronts. To remedy this issue,a large body of research has been performed in recent years and many new algorithms have been proposed. This paper provides a comprehensive survey of the research on MOPs with irregular Pareto fronts. We start with a brief introduction to the basic concepts, followed by a summary of the benchmark test problems with irregular problems, an analysis of the causes of the irregularity, and real-world optimization problems with irregular Pareto fronts. Then, a taxonomy of the existing methodologies for handling irregular problems is given and representative algorithms are reviewed with a discussion of their strengths and weaknesses. Finally, open challenges are pointed out and a few promising future directions are suggested.

I. INTRODUCTION

MOST real-world multi-objective optimization problems(MOPs) [1] are constrained [2], redundant [3], or highly nonlinear [4], resulting in irregular Pareto fronts (PFs), which may be discontinuous [5], degenerate [6], or inverted [2].Solving MOPs with irregular PFs is challenging, since there is no a priori knowledge about the shape of the PFs, making it particularly tricky to design efficient optimization algorithms.

Over the past decades, evolutionary algorithms have witnessed great success in solving MOPs and a large number of multi-objective evolutionary algorithms (MOEAs) have been proposed [1]. Generally, MOEAs can be classified into four categories. The first category includes the decompositionbased MOEAs, which decompose the target MOP into multiple subproblems and the solution of each subproblem forms the final solution set. For example, MOEA/D [7] and RVEA [8] both perform decomposition by means of a set of predefined weight or reference vectors and optimize the subproblems simultaneously. The dominance-based MOEAs belong to the second category. In these algorithms, a nondominated sorting mechanism along with a diversity maintenance scheme is used to select candidates. For example,NSGA-II [9] uses a crowding distance as a diversity measure in selection after ranking the candidate solutions with the fast non-dominated sorting method. The indicator-based MOEAs fall in the third category. In these algorithms, such as HypE[10] and IBEA [11], candidate solutions that contribute more to the performance indicator are selected. Coevolutionary MOEAs [12] fall in the fourth category, which use coevolutionary algorithms to deal with MOPs. For example, a preference-inspired co-evolutionary algorithm using weights(PICEA-w) is developed in [13] to co-evolve the weights with candidate solutions, thereby eliminating the requirement to predefine appropriate weights before optimization starts.

However, it has been found that MOEAs designed for regular MOPs are very likely to fail to perform well when solving MOPs with irregular PFs [14], [15]. For example, for decomposition based MOEAs using a set of fixed and uniformly distributed weight vectors, not every weight vector can intersect with the PFs since irregular PFs are distributed only in a part of the objective space [4]. Consequently, many predefined weight vectors are wasted, making it hardly possible to approximate the whole PFs. Fig.1(a) shows a biobjective optimization problem with a discontinuous PF(denoted by the blue line), where the circles represent the candidate solutions, and the lines with arrows represent uniformly distributed reference vectors used in the traditional decomposition based algorithms. As there are only two intersections between PF and reference vectors, only two individuals, which are represented by orange solid circles, can be selected from the candidates, so we can not approximate the complete PF. Likewise for dominance based MOEAs [9],most diversity maintenance mechanisms assume that the PF is regular and therefore cannot work properly when the PFs are irregular. As shown in Fig.1(b), individual M will be selected because it can significantly improve the diversity. However, it is obvious that the individuals selected in this way do not well represent the actual PF shape. Finally, for indicator based MOEAs [10], [16], individuals that contribute more to the indicator will more likely to be selected, which may favor some dominated solutions that can contribute more to the indicator over non-dominated solutions. For example, for an MOP with a degenerate PF, the PF is distributed only in a very narrow region of the objective space. In this case, many dominated individuals scattered in other regions of the objective space may contribute more to the hypervolume (HV)indicator [10], which may mislead HV indicator based environmental selection methods. An example is shown in Fig.1(c), in which individual M contributes more to the HV indicator than individuals N1and N2. As a result, M will be selected, which cannot contribute to the achievement of a diverse Pareto optimal solution set.

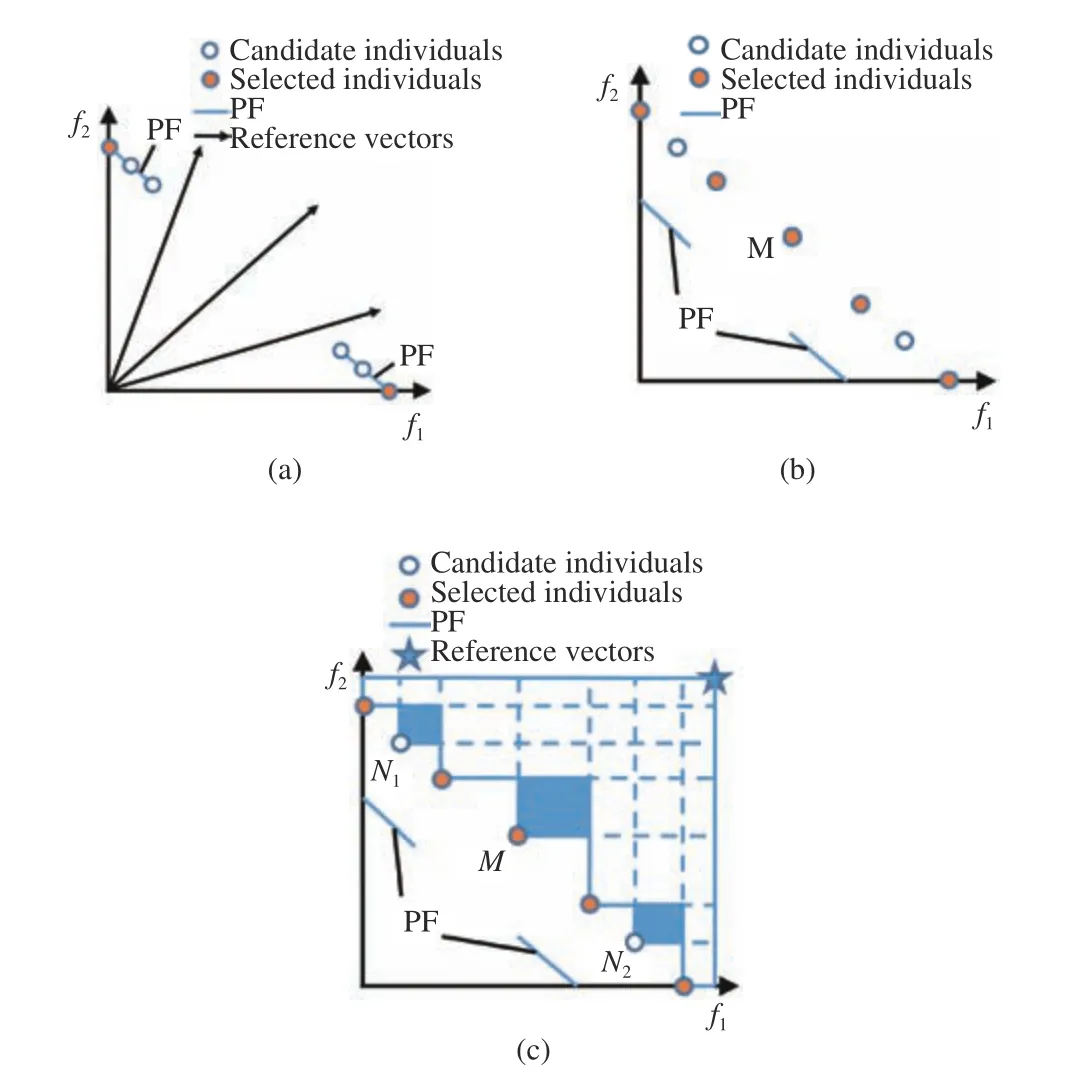
Fig.1. Illustrative examples showing the difficulty when traditional(a) decomposition, (b) dominance, and (c) indicator based MOEAs solve MOPs with irregular PFs.

In recent years, MOPs with irregular PFs have attracted increasing attention in the field of MOEAs. A large number of MOEAs have been proposed for addressing irregular PFs [4],[17]–[19]. These MOEAs can roughly be divided into four categories. The first category of MOEAs for solving irregular MOPs adopts an auxiliary selection method working together with a set of fixed reference (weight) vectors [20]. In the second category, reference vectors are adjusted during the search process [4] according to the population distribution,aiming to generate a set of reference vectors that match the distribution of the PF. In the third category, reference points can also be used to guide the search process in dealing with irregular PFs [14]. In this kind of algorithms, the reference points are used to both measure the convergence of individuals and maintain the diversity of the population. The fourth category of MOEAs handling irregular problems intends to cluster the population [21] or use grids [22] to divide the whole objective space into a number of sub-regions.Thus, optimal individuals in each sub-region can be selected to form the final population. A taxonomy of MOEA methods for MOPs with irregular PFs are listed in Fig.2.

This paper aims to provide a comprehensive review, for the first time to the best of authors’ knowledge, of existing MOEAs for solving MOPs with irregular PFs to provide insights into the strengths and weaknesses of these algorithms,discuss remaining challenges, and outline future research directions. It should be noted that challenges in solving MOPs with irregular Pareto fronts are different from those in addressing multi-modal multi- / many-objective optimization problems, where the main motivation is to promote diversity in both decision space and objective space [23]–[27].

II. FUNDAMENTALS

A. Definition

Fig.2. A taxonomy of MOEA methods for MOPs with irregular PFs.

Fig.3. Ideal point, nadir point, and worst point.

The uniformly distributed reference vectors can be constructed from the uniformly distributed reference points and the origin. Fig.4(a) shows an example consisting of 15 uniformly distributed reference points and Fig.4(b) shows the 15 uniformly distributed reference vectors generated using the reference points.

In decomposition based evolutionary algorithms, a reference point or vector is said to be active if there is at least one solution that is associated to the reference point or vector.Otherwise, it is called inactive [30], [31].

Fig.4. A set of uniformly distributed reference points (a) and reference vectors (b).

As their name suggest, the boundary points are solutions along the boundary of PFs. Note that the number of extreme points is m ( m is the number of objectives), while the number of boundary points is infinite. An example is given in Fig.5 to show the difference between boundary and extreme solutions.The boundary solutions in Fig.5(a) are located on the boundary of the PF, which is denoted by red solid lines, and the extreme solutions are denoted by red stars in Fig.5(b).

Fig.5. An illustrative example of boundary solutions and extreme solutions.

III. MOPS WITH IRREGULAR PFS

A. Definition of Irregular Problems

A regular PF indicates that the PF has a simplex-like shape,where all the vectors with positive directions intersect with it when its ideal point is the origin, as mentioned in [33]. All other shapes of PFs are called irregular PFs. In particular, let∀v=(v1,...,vm) be a vector, subject to vi≥0 (i ∈1,...,m),

where, v can be any vector in the first quadrant. Equation (5)means that there does not exist any v that does not intersect with the regular PF. In other words, all vectors with positive directions intersect with the regular PF. In (6), we replace the symbol ∄ with ∃, which means if a Pareto front is irregular,there must be a v that does not intersect with the Pareto front.

Fig.6 shows four regular PFs, the black surface represents the PF, the blue arrowed line represents the positive direction vector, and the intersection of the vector and the PF is represented by a red solid circle. We can see that no matter whether the PF is linear, convex, concave, or non-convex, the PF is regular as long as (5) holds.

Fig.6. Regular PFs which is (a) linear, (b) convex, (c) concave and (d) nonconvex.

However, the PFs in the real world are not always regular.In reality, the shapes of the PFs may be discontinuous,degenerate or inverted. Fig.7 shows a (a) regular, (b) discontinuous, (c) degenerate, and (d) inverted PF of three-objective problems, where the black surface represents the PF, the blue arrowed line represents the positive direction vector, and the intersection of the vector and the PF is represented by a red solid circle. The three coordinate axes represent the objective values of the three objectives. Fig.8 shows the parallel coordinate plots of a (a) regular, (b) discontinuous, (c) degenerate, and (d) inverted PF of 5-objective problems. The x-axis represents the objective numbers, and the y-axis represents the objective values. We can see that irregular PFs are a part of regular PF. Therefore, as described in (6), there will be positive direction vectors that do not intersect with the irregular PF.

Fig.7. Examples of different types of Pareto fronts. (a) Regular, (b) Discontinuous, (c) Degenerate, and (d) Inverted PF.

Fig.8. Parallel coordinate plots of Pareto optimal solutions sampled from various types of Pareto fronts. (a) Regular, (b) Discontinuous, (c) Degenerate,and (d) Inverted PF.

B. Causes of Irregular PFs

In the following, we discuss the reasons why the Pareto fronts become irregular according to the type of irregularity.

1) Degenerate PFs: Degenerate problems are those that have non-essential objectives. Here, essential objectives mean the objectives that actually determine the shape of PFs.Degenerate problems can be divided into three categories:explicitly degenerate, implicitly degenerate, and partially degenerate. Explicitly degenerate problems are usually resulted from non-essential objectives that are formulated by a linear combination of the essential objectives. However, if the non-essential objectives are formed by a nonlinear combination, or a combination of the transformed essential objectives, then such MOPs are implicitly degenerate problems. To solve implicitly degenerate problems, the algorithm must be able to extract the essential objectives, making them harder to solve.Reasons for partially degenerate problems are that some parts of objective space are conflicting with each other, while other parts are not. This may happen when the objective functions corresponding to different regions of decision space are different. Apart from the above, there is a special kind of degenerate problems, called multi-point or multi-line distance minimization problem [34]. The property of these kinds of problems is that the manifold of the decision variables is always two-dimensional. The distribution of the observed solutions in the objective space can be directly observed from their distribution on the decision space.

TABLE I TEST PROBLEMS WITH IRREGULAR PFS

2) Discontinuous PFs: By discontinuous problems, we usually mean that the Pareto optimal fronts are discontinuous while the Pareto optimal set in the decision space is continuous. A discontinuous PF is usually caused by the fact that some regions are dominated by other regions. For example,discontinuous segments may be resulted from changing the shape function of a PF in designing benchmark functions, e.g.,DTLZ7 [35], or even from some constraints on the decision variables that make some regions infeasible, e.g., C2-DTLZ2[36].

3) Inverted PFs: An inverted PF can be formed by turning a regular PF upside down. So inverted PFs can be resulted from inverted objective functions. For instance, inverted DTLZ1[2], Inv-DTLZ1 for short [36], is obtained by making a transformation of the function value of DTLZ1 problem [35](which has a regular PF) by using the expression fi(x)←0.5(1+g(x))−fi(x), where g(x) is defined in DTLZ1[35].

The inverted PFs of Inv-DTLZ2 [36] and MaF1 [37] are formed in a similar way. That is, DTLZ1–1–DTLZ4–1[15] and WFG1–1–WFG9–1[15] multiply the objective function values of DTLZ [35] and WFG [38] problems by –1 to construct inverted PFs. In addition, constraints are another reason that causes inverted PFs. For example, C-DTLZ1 [36] is created by adding a hyper-cylinder (with its central axis passing through the origin and equally inclined to all the objective axes) as a constraint so that only the region inside the hypercylinder is feasible. Meanwhile, some inverted PFs are caused by the functions themselves. The construction of the function itself makes the areas outside the inverted PF area dominated,for example, MaF4 [37].

4) Other Shapes of Irregular PFs: The irregular PFs of IMOP4–IMOP8 [33] are caused by the functions themselves.The construction of the function itself makes the areas outside the irregular PF area dominated. Meanwhile, constraint is another reason that causes various shapes of irregular PFs.The widely used multi-objective test problems with irregular Pareto fronts are summarized in Table I.

C. Real World Problems With Irregular PFs

Many real-world MOPs with irregular PFs have been reported. The irregular PFs result from constraints [2],redundancy [3], or high nonlinearity of the objective functions[4]. For example, the three-bar truss optimization problem[57] aims to minimize the volume of the trusses and the combined nodal displacement under the constraints on the area and allowed stress for each element. The PF of the biobjective optimization problem consists of two separate pieces of linear curves. The mineral processing production planning problem [58] is a nonlinear MOP with five objectives, namely maximization of the concentrate grade, minimization of the total beneficiation ratio, maximization of the metal recovery,and minimization of the cost of concentrate. The PF of this mineral processing production planning problem is also discontinuous. Crash worthiness in vehicle design [2] is a three-objective unconstrained optimization problem and the PF of this problem is distributed in two separate regions.Other real-world optimization problems having discontinuous PFs include the two-objective carbon fiber drawing problem[14] and the car-side impact problem [2].

The three-objective multispeed gearbox design optimization problem aims to minimize the overall volume of the gear material used, which is directly related to the weight and cost of the gearbox, maximize the power delivered by the gearbox,and minimize the center distance between the input and output shafts. The minimization of the overall volume of gear material used and the minimization of the center distance between input and output shafts are non-conflicting, while each of them is in conflict with the maximization of the power delivered by the gearbox. As a result, the PF of this problem is degenerate. Finally, the multi-objective traveling salesman problem [59] is a three-objective optimization problem which has an inverted PF.

IV. MOEAS FOR MOPS WITH IRREGULAR PFS

In this section, we are going to provide an overview of existing MOEAs dedicated to solving MOPs with irregular PFs. From the literature that can be found at the time of submission, we choose one or two algorithms to illustrate each different idea. Thus, we cannot guarantee that all relevant references are covered due to space limit. Here, the MOPs are categorized into four groups according to their main mechanism for handling irregularity in the PF.

A. Fixed Vector based MOEAs With Auxiliary Methods

The fixed vectors produced by the Das and Dennis’s systematic approach are widely used in decomposition based MOEAs [4], [60]. Individuals are assigned to the closest vector such that the problem is divided into several subproblems. Then the best solution from each sub-problem will be selected to construct the final population. However, when dealing with irregular PFs, there are vectors that do not intersect with the PF, consequently, the remaining active vectors cannot select enough individuals to approximate the complete PF. Therefore, auxiliary methods have been added to improve the performance of the fixed vector based MOEAs in dealing with irregular PFs.

One idea is to use non-dominated sorting or an external archive to select more individuals to improve the diversity of the population. For example, BCE-MOEA/D [61] uses a Pareto-based criterion to compensate for the possible diversity loss of MOEA/D, while MOEA/D-AED [62] proposes a new archiving strategy to store non-dominated individuals with a higher fitness value selected by MOEA/D. In BCE-MOEA/D[61], two populations are adopted, one based on nondominated sorting and the other on decomposition. These two populations exchange the information during the search process, and the complementary effect of the two populations makes it possible to solve irregular problems. In MOEA/DAED [62], a solution can be randomly picked up from the archive to produce a weight vector to guide the selection of solutions for mate selection if a sub-problem cannot be optimized for several generations. Note that the random weight vector is just for determining the solutions for mate selection.

In traditional decomposition based MOEAs, each subproblem is associated with one and only one solution. The underlying assumption is that each sub-problem has a different Pareto optimal solution, which may fail to hold for irregular PFs. That is one of the reasons why MOEA/D or its variants fail to perform well on irregular problems. So another idea is to allow different solutions to be associated with the same sub-problems and allow some sub-problems to have no solution associated. For example, in MOEA/D-SAS [17], a number of individuals are allowed to be associated with the same active reference vector. The individuals in each subproblem are sorted first according to their fitness values, and then according to the angles between other individuals.Similarly, in ASEA [63], the individuals associated with the same active vector are first sorted by convergence, and an angle based crowding degree evaluation method is then used to further screen the individuals in the lower convergence ranking. This makes it possible to solve irregular problems even with only one set of fixed reference vectors.

Some researchers also propose to solve irregular problems by using two sets of fixed reference vectors, one starting from the ideal point and the other originating from the nadir point.An example is given in Fig.9. It can be seen that only part of a set of evenly distributed reference vectors cover the inverted PF. By contrast, a set of reference vectors starting from the nadir point can cover the whole inverted PF. Thus, some work has been done along this line. In PAEA [64], MOEA/AD [65],and MOEA/D-MR [20], two sets of fixed reference vectors are adopted to handle problems with inverted PFs. PBI and inverted PBI scalarizing functions based on these two sets of reference vectors (starting from ideal point and nadir point,respectively) are simultaneously used in PAEA [64] to evaluate the solutions in the population during the search process. The scalarizing function for each set of reference vectors can be different or the same. PBI and an augmented achievement scalarizing function (AASF) are adopted for each set of the reference vectors in MOEA/AD [65], accounting for convergence and diversity, respectively. Moreover, the information based on the ideal point and the nadir point also involves in mate selection in MOEA/AD [65]. Different from PAEA [64], MOEA/AD [65], two scalarizing functions based on ideal point and nadir point are separately adopted in two stages of the search process in MOEA/D-TPN [54]. In the first stage, only the ideal point based Tchebycheff approach is used to guide the search, in which the reference vectors are divided to intermediate subset and extreme subset, respectively. If the solutions found at the end of the first phase indicate the crowededness of the population found by the intermediate subset and extreme subset reference vectors are not balanced,then the second search phase guided by the nadir point based Tchebycheff approach will be adopted. In DBEA-DS [66],two sets of solutions are obtained in each generation with two sets of reference directions. Even though two sets of reference vectors are used simultaneously, only one set of solutions of the least fitness value will survive. In MOEA/D-MR [20], two fixed reference vector sets using the ideal point and the nadir point, respectively, as the origin are adopted, however, only one kind of scalarizing function is adopted, instead of using two different scalarizing functions for two sets of reference vectors. Each solution in the population is associated to a number of nearest subproblems.

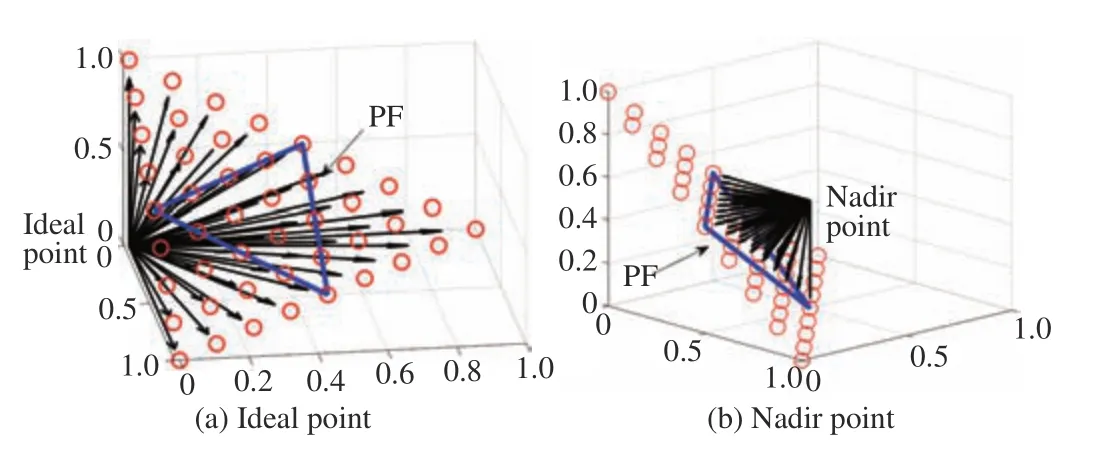
Fig.9. Two set of reference vectors originating from the ideal point and nadir point, respectively. The true PF is located inside the inverted triangle.

As mentioned above, decomposition based methods with fixed vectors can be used to handle problems with irregular problems by using auxiliary methods, such as non-dominated sorting, archive, lifting the limit on the number of optimal solutions for each sub-problem or adopting two sets of reference vectors.

The MOEAs with a fixed reference vector in combination with an auxiliary method for solving irregular MOPs are summarized in Table SI of the Supplementary materials.

B. Reference Vector Adjustment Based MOEAs

Decomposition based algorithms with evenly distributed reference vectors or weight vectors may not be suited for dealing with irregular problems since the predefined reference vectors may not match well with the shape of the PFs. Thus,one intuitive idea is to adjust the distribution of reference vectors during the search process to adapt them to the distributions of solutions in the population. For solving irregular problems, effective generation of new promising solutions and selecting promising solutions both play important roles in decomposition based algorithms. However, most existing algorithms put more emphasis on the selection process and largely neglect the effective generation of promising solutions. Most algorithms adapt the reference vectors to guide the search process in environmental selection, while only few algorithms, e.g., IM-MOEA [67], [68], study how to generate newer promising solutions.

For different decomposition based methods, different scalarizing functions are adopted and designed to guide the search process, such as weighted sum, Tchebycheff, penaltybased boundary intersection (PBI) in MOEA/D [7], the anglepenalized distance (APD) in reference vector guided algorithm (RVEA) [8]), and a few variants of PBI proposed in recent years [69], [70]. The adaptation of reference vectors heavily depends on the scalarizing functions since the contour lines of the scalarizing functions determine the trajectory of search process. The scalaring functions will directly influence the balance of convergence and diversity for an algorithm. For instance, the weighted sum method ensures that algorithms converge faster than other scalarizing fuctions [71] as the contour line of weighted sum scalarizing function is a hyperplane that divides the whole objective space into two parts.Fig.10 plots the contour line of weighted sum and Tchebycheff scalarizing functions. It can be seen that the contour line for the weighted sum scalarizing function is perpendicular to the reference vectors. Therefore, the adaptation of reference vectors should take both the shape of the PFs and the adopted scalarizing functions into consideration when we solve irregular problems.

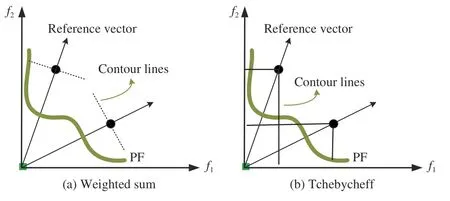
Fig.10. The contour line for weighted sum and Tchebycheff scalarizing function.

To handle irregular problems, the reference vectors should be adjusted to make them match well with the solutions during the search process. However, several difficulties may be encountered when adjusting the reference vectors. The first concern is which reference vector(s) should be adjusted. We know that even for solving regular problems, sometimes a reference vector can become inactive, let alone for solving irregular problems. The second question is when the reference vectors should be adjusted. If the reference vectors are adjusted too frequently, it may slow down the convergence speed. If the reference vectors are not adjusted in time, on the contrary, promising regions may get lost. Finally, how should the reference vectors be adjusted?

In the following, we divide the methods for adjusting reference vectors into three main categories: 1) utilizing the solutions to generate the reference vectors, 2) adjusting reference vectors using existing reference vectors, 3) adjusting reference vectors by learning the distribution of PFs.

1) Utilizing Solutions to Generate Reference Vectors: Using solutions in the population or in the archive to replace the inactive reference vectors or to generate new reference vectors is intuitive since the solutions themselves indicate which regions are promising. However, the solution vectors may not be directly used as weight vectors. As pointed out in [72],[39], the reference vectors are in inverse proportion to the search directions of solutions in the Tchebycheff method [72],[48]. An example is given in Fig.11, where it can be seen that the weight vector or reference vector is not in the same direction of the solution vector (the solution denoted by a solid circle is associated with reference vector λ). That is to say, when the Tchebycheff scalarizing function is adopted to guide the search process, the solution vector has to be transformed to its inverse direction, to serve as a reference vector. Therefore, the adopted scalarizing function should be taken into consideration when a solution is adopted to be transformed to a reference vector.

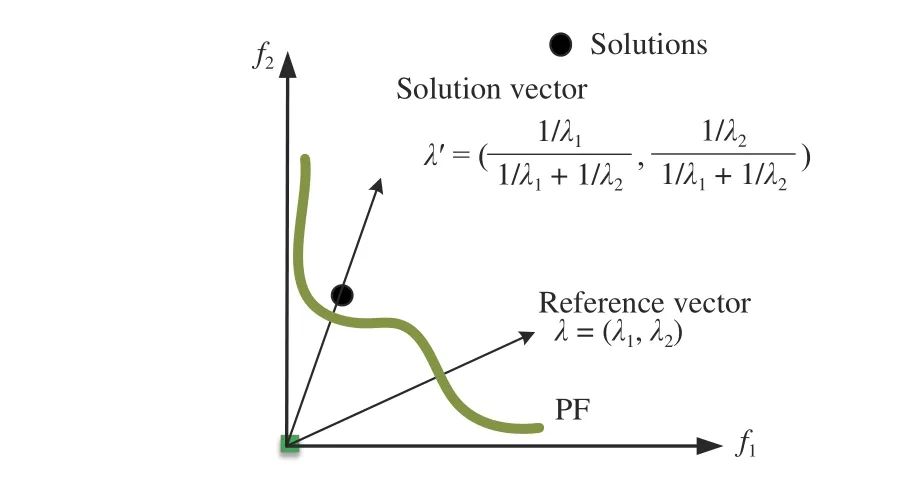
Fig.11. An illustrative example of the difference between a solution vector and a reference vector when Tchebycheff scalarizing function is used.

The most common way is to use the solutions in an archive to generate new reference vectors, e.g., [39], [73], [74], since the archive contains all historical non-dominated solutions compared with the current population, making the adaptation of reference vectors more accurate and stable. In MOEA/DAWA [39], an archive is preserved to evaluate the sparsity of reference vectors using a vicinity distance. After a number of fixed generations, those crowded reference vectors will be deleted and new reference vectors will be added in sparse regions using the solutions in the archive. Same as MOEA/DAWA [39], the sparsity level based on the Euclidean distance is adopted in [75]. In [74], the solutions in the archive are used to detect promising regions and a set of solutions are picked up from the archive to generate the corresponding weight vectors after a number of fixed generations. However, in [76],the generation of the reference vectors using the solutions in the archive is only triggered at the late stage of the search process.

Apart from using solutions in the external archive, some algorithms also use solutions both in the archive and in the current population as the candidate reference vectors[77]–[80]. In [77], the entropy between reference vectors and the solutions is checked after a number of fixed generations to decide whether the adaptation of reference vectors should be invoked. If the number of active reference vectors is insufficient, new reference vectors will be generated by selecting several solutions from the non-dominated solutions from the current population according to the cosine distance. Since it is hard to determine the frequency of adjusting the reference vectors, using entropy as the criterion ensures that when to adjust the reference vectors becomes more appropriate. In LCMaOEA [81], the cluster center vectors generated by clustering the individuals mapped on the hyperplane are used as the reference vectors, and a vector-based PF area detection method is proposed to determine when to adjust the reference vectors. In MOEA/D-AM2M [43], the objective space is divided into several big subregions and the reference vectors are reallocated after a number of fixed generations. The number of reference vectors in each sub-region is decided by the number of solutions in each sub-region and reference vectors are generated by picking up a solution vector with the biggest angle to the existing reference vectors. This method performs well in MaOPs with degenerate as well as discontinuous PFs. Different from MOEA/D-AM2M, the weight vectors in [59] are adjusted when the lowest temperature is reached with simulated annealing as local search and only those solutions satisfying the predefined two conditions that take both the distance between the reference vectors and the distance between the neighbouring solutions into consideration will be adjusted. In [82], the solutions contributing more to the hypervolume of the current population will be picked up to generate the reference vectors.

It can be concluded that solutions with the largest similarity in terms of the Euclidean distance or cosine distance to the existing active references are usually picked up for generating reference vectors. Selecting solution vectors having the largest cosine distance to the existing active reference vectors to replace the inactive reference vectors can ensure the diversity of the population [43], [83], [84]. For instance, in g-DBEA[83], an inactive reference vector is replaced by the solution with the maximum angle to its neighbouring reference vectors with more than one solution attached to.

Using solutions in the current population or in an archive for generating reference vectors means either the historical or current distribution information is used for guiding the search process. The adaptation of the reference vectors can happen at every generation or after a number of fixed generations, no matter whether the solutions in the archive or in the current population are used. The advantage of adapting the reference vectors after a number of fixed generations is that the convergence speed is not slowed down since the adapted reference vectors keep unchanged in-between. However, the disadvantage is that the promising solutions or regions may get lost if there is a rapid change in the distribution of the population. If the reference vector is adjusted whenever an inactive reference vector emerges, the promising region can be quickly located, at the expense of convergence speed being slowed down since inactive reference vectors are adjusted frequently[85], [86].

2) Adjusting Reference Vectors Using Existing Ones:Solutions in the archive or in the current population only represent the regions that have already been covered.However, it is also important to predict which region is more promising in addition to the already covered regions. Therefore, the generation of new reference vectors can also rely on the information of the existing promising reference vectors to explore unexplored promising regions. Several studies have been done along this line. In [87], [30], the search is divided into two phases. In the first phase, the search is done along the boundary reference vectors. In the second phase, new reference vectors are generated by disturbing the “good” reference vectors based on the penalty values in [87], while inactive reference vectors are replaced by the interpolation between active reference vectors based on the Euclidean distance between the reference vectors in MOEA/D-2ADV [30]. As shown in Fig.12, a new reference vector V5is generated by the interpolation of active reference vectors V2and V3since they are of the largest Euclidean distance between all active reference vectors. The consideration here is that the region in the middle of the active reference vectors should also be promising. In MOEA/D-ABD [5], the endpoints of each discontinuous region of the PFs are first detected for solving discontinuous problems. In addition, the weight (reference)vectors are then divided into two sets according to whether they have intersections with the PFs and are adjusted using different step sizes accordingly within each discontinuous segment of PFs. However, MOEA/D-ABD can only handle two-objective problems. A-NSGA-III [2] and A2-NSGA-III [36] are proposed to handle problems with irregular PFs based on the framework of NSGA-III [32]. The predefined reference points for guiding the search are not replaced in A-NSGA-III even some of them are inactive. Instead, more reference vectors are sampled around the promising reference vectors whose niche count is more than one. Same as the adaptation method in A-NSGA-III, an indicator called the median of dispersion of the population (MDP) is proposed to determine when the adaptation should be triggered [88]. Similarly,denser reference vectors are generated until the number of active reference vectors is larger than the population size [89].

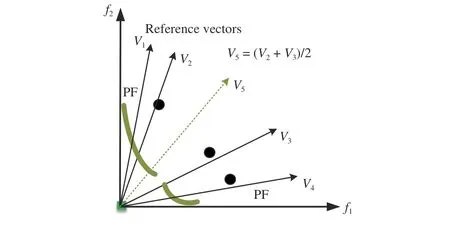
Fig.12. An illustrative example of generating a new reference vector by interpolation.

In summary, more promising regions may be explored by interpolating reference vectors or generating denser reference vectors around promising regions by utilizing the information of the active reference vectors. However, sampling reference vectors near the active reference vectors does not perform well on dealing with degenerate PFs or problems with small pieces of PFs since it is hard to correctly sample reference vectors on PFs if the PFs occupy very small parts of the whole PFs, especially when the number of objectives is large.

3) Learning the Distribution of PFs: It is known that where to adjust reference vectors remains a challenge for decomposition based methods with adaptive reference vectors. Maladaptation of reference vectors may slow down the convergence or cause a loss of promising solutions. Thus, it is expected that the distribution of PFs can be continuously learnt from the solutions in the population at each generation.

It is difficult to determine how frequent the reference vectors should be adapted and which reference vectors should be adjusted for handling irregular problems. To answer these questions, Gu and Cheung [42] propose to use the selforganising map (SOM) network to learn the topology of PFs,termed MOEA/D-SOM. The proposed MOEA/D-SOM can gradually learn the topology of PFs during the search process and the nodes of the SOM serve as the positions of the reference vectors. Following this idea, a very recent work,DEA-GNG [90] proposes to train a growing neural gas (GNG)network to learn the topology of the PFs. By training the GNG network, all reference vectors are adjusted gradually in each generation. Different from DEA-GNG, an improved GNG(iGNG) is designed for timely yet steadily adapting the reference vectors to handle the changing distribution of the population in RVEA [91]. Note that this kind of methods using SOM or GNG to learn the topology of PFs is different from the traditional methods that merely adjust the inactive reference vectors. All reference vectors in MOEA/D-SOM,DEA-GNG, and RVEA-iGNG have a chance to be adapted by training the SOM or GNG network in each generation, no matter whether they are inactive or not.

In [31], the status of activeness of the reference vectors is learned by training a support vector machine (SVM). A set of evenly distributed reference vectors will be sampled after a number of fixed generations to make sure that the number of active reference vectors reaches the population size [31]. This method is very fast and efficient despite that the training of the SVM is required. However, the drawback of this method is that a huge number of reference vectors are needed to be sampled for irregular MaOPs, especially for problems with degenerate PFs. In [92], reference vectors in different subregions are assigned based on the complexity of each region, in which it is believed that the regions with a larger number of solutions are closer to the PF than others.

The distribution of the reference vectors can also be learned by periodically estimating the geometry of the PFs and then reference vectors can be sampled based on the geometry. PFs are learned by Gaussian process regression models in [93],[94], in which an arbitrary objective serves as the target, while the remaining objectives are used as the input of the GP regression model. The method of estimating PFs is not sensitive to the shape of PFs, regardless of the convexity of the PFs. In PICEA-w [13], the solutions in the population are coevolved with the reference vectors, which is also a promising method in solving irregular problems.

Compared with the other adaptation methods, adaptation of the reference vectors by learning is believed to be more precise if both the historical and current distribution information of the solutions are used.

Overall, when, where and how to adapt the reference vectors should be considered when dealing with irregular problems. Striking a balance between achieving quick convergence and maintaining a sufficient degree of diversity according to the adaptation of reference vectors remains a challenge in dealing with irregular problems, especially for MaOPs. We can find that learning the distribution of reference vectors by using machine learning models such as SOM, GNG, SVM seems promising compared with the traditional methods of adapting inactive reference vectors. Moreover, no matter in which way the reference vectors are adjusted, we need to pay more attention to some specific points in the search space,such as the ideal point and nadir point, and a proper normalization of solutions. As discussed in [95], different approaches to normalization significantly impact the performance of the algorithms, especially when there are dominance resistant solutions [96] in the population.

MOEAs with an adjusted reference vector for handling irregular Pareto fronts are summarized in Table SII of the Supplementary material.

C. Reference Point Based MOEAs

In addition to the reference vectors, it is also popular to use reference points to guide the search in multi-objective optimization. Similar to reference vectors, reference points generated by the traditional Das and Dennis’s approach cannot match irregular PFs and the reference points usually need to be adjusted according to the population distribution, or new reference points need to be generated in the population.

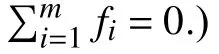
2) Utilizing Individuals to Generate Reference Points: One disadvantage of the reference point adjustment methods based on existing reference points is that it cannot adapt well to the distribution of the population within a limited number of iterations, resulting in a waste of reference points. The idea of utilizing individuals to generate reference points can alleviate this issue. More specifically, a set of reference points with good performances in convergence and diversity are continuously generated by the current population to guide the evolutionary search. For example, in RPEA [99], the nondominated individuals with a higher level of diversity will be chosen to generate reference points. The reference points are updated once every a few iterations by reducing the corresponding objective values of the chosen individuals.Instead of using the coordinate values of individuals to generate reference points, CA-MOEA [14] uses a hierarchical clustering method to combine individuals into several clusters,and then use the cluster centers as the reference points.Although generating reference points with individuals can effectively improve the reference points, frequent changes to the distribution of the reference points may slow down the convergence speed.

3) Differences Between Reference Points and Reference Vectors: Although reference points and reference vectors appear similar, there are subtle differences in using reference points and reference vectors. A reference point can represent the position of an individual more precisely than the reference vector, while a fixed reference vector can lead to faster convergence of the evolution process. First of all, when an MOP is divided into sub-problems, each reference point forms a sphere or hypersphere around it, in which all solutions will be associated to the reference point. By contrast, a reference vector forms a cone or hypercone around the vector. As a result, in reference point based methods, the individual closest to the reference point will be selected from each sub-problem,while in reference vector based methods, an individual will be selected based on the scalarizing function, which depends on the solution’s relative position to both the ideal point and reference vector. Fig.13 shows an example of the difference in using reference points and reference vectors, where the shaded area around each reference vector indicates the region in which solutions will be assigned to the reference vector according to the angle only, and the solid circle represents the area in which individual are assigned to the reference point. In the figure, “A”, “B”, “C”, “D”, “E” , and “F” are six individuals in a two-objective space, “R1” and “R2” are two reference points, “V1” and “V2” are two reference vectors.We can see that since the angle and the vertical distance between reference vector “V2” and individual “D” are smaller than “V1”, “D” is associated with reference vector “V2”.However, because reference point “R1” is closer to individual“D” than “R2”, “D” is assigned to reference point “R1”. So“A”, “B”, “C”, and “E” are assigned to “V1”, while “D” and“F” are assigned to “V2”. “A”, “B”, “C”, “D”, and “E” are assigned to “R1” , while “F” is assigned to “R2” . In environmental selection, “R1” will select “A” as “A” is the closest to “R1”, while “V1” will select “C”, since “C” is closest to the ideal point. When dealing with irregular PFs,reference vectors matching the location of the PF can help the population converge to the PFs, while the reference point matching with distribution of the PFs can maintain good diversity.

Fig.13. An illustrative example of the differences in using reference points and reference vectors.

Reference point based MOEAs for handling irregular MOPs are listed in Table SIII of the Supplementary material.

三、(满分25分)2016年7月19日，河北邢台市区突降暴雨，市区多处路段积水严重，此时一公交车行驶至某路段靠近桥下时发现积水严重，情况不妙，立即掉头驶离危险路段．当时的情况如下图所示．获悉此事后，很多人都很惊讶，在这么窄的路上实现掉头简直不可思议！

D. Grid or Clustering Based MOEAs

Grid or clustering based MOEAs use grids or clustering methods to divide the population into a number of subregions, and the optimal individuals of each sub-region constitute the final population. Usually only one individual is selected from each sub-region, so the distribution of the subregions directly affects the distribution of the final solution set.

1) Grid Based Division: Grid based methods divide the objective space into several grids using specific points, each grid representing a sub-problem. So the sub-problems formed by the grid methods have clear boundaries. Since the distribution of the individuals may not be even, some subproblems may contain multiple individuals, and others may be empty. Usually, the best individuals in each grid will be selected to form the final population, however, since the number of effective sub-problems is not known beforehand,multiple individuals may be selected in each grid.

In the following, we discuss some representative grid based MOEAs for MOPs with irregular PFs. In RdEA [18], the middle points between each two extreme points of a region are used for defining the grid. The above procedure can be repeated on each sub-region to divide it into smaller subregions until the number of divisions is satisfied. However,the proposed region division method may not be practical for MaOPs, and it is difficult to determine which region an individual is located in. In addition, there are other parameters that are difficult to specify. CDG-MOEA [22] constructs a grid system according to the number of segments along each objective axis, and then assigns grid coordinates to each individual according to its grid. In the environmental selection, the individuals with good convergence in each grid are selected. MOEA-PPF [100] determines the discontinuous points on the PF according to the crowded distance between the individuals, and divides the objective space into several sub-problems using the discontinuous points. The algorithm is more suited for problems with discontinuous PFs, although correct judgments of the discontinuous points are nontrivial.Illustrative examples of the grid generation method proposed in the above three MOEAs are given in Fig.14.

Fig.14. Illustrative examples of the grid generation method in (a) RdEA,(b) CDG-MOEA, (c) MOEA-PPF.

The artificially divided grids may ensure the uniformity of the partition to a certain extent. Since a lot of information such as individual distribution cannot be predicted beforehand,however, it is likely to produce invalid sub-problems.Moreover, it is difficult to determine the selection of the division points, the number of grids, and other important parameters, making the grid-based methods difficult to be used.

2) Clustering Based Division: In addition to grid based methods, clustering is another effective way to partition the population. Unlike the grid based methods, clustering based methods do not have clear-cut artificial boundaries. Clustering is well suited for MOPs with irregular Pareto fronts, because clustering divides the population based merely on the similarity of the individuals. Clustering methods group similar individuals into one sub-problem, consequently, there must be at least one individual in each sub-problem, thus avoiding invalid divisions. However, the linkage criterion and the distance measurement of the clustering method, and the environmental selection mechanism based on clustering will heavily affect the performance of the algorithm.

Some algorithms use pre-defined cluster centers to divide the entire population. Individuals are assigned to the cluster where the nearest cluster center is located. This method is very intuitive and simple, but when dealing with irregular PF problems, the predefined clustering centers may not match the shape of the PFs, which may lower the clustering performance. CLUMOEA [101] uses the k-means clustering method to partition the population for mate selection, in which only individuals in the same cluster will be selected to produce offspring individuals to accelerate convergence.However, inherent limitations of the k-means cluster algorithm, such as the sensitivity to the initial cluster centers,the assumption of spherical data distributions, and the difficulty in determining the number of clusters, seriously impair the performance of CLUMOEA. The cluster centers are also predefined in F-DEA [102], which uses the less crowded reference points from the active reference points generated by Das and Dennis’s approach as the cluster centers. The individual with the best fitness value in each cluster will be selected to construct the final population.However, in an MOP with irregular Pareto fronts, the active reference points generated by the Das and Dennis’s approach may be so few that the population cannot be divided into a sufficient number of sub-regions.

Sometimes, two different clustering methods may be used in an algorithm. For example, MaOEA/C [21] first takes the axis vectors as the clustering centers to roughly partition the population, then performs hierarchical clustering in each subcluster. The individual with the best convergence in each subsub-cluster is selected after hierarchical clustering. In mate selection, there is a certain probability at which only individuals in the same axis-vector-centered cluster are selected to enhance the exploration ability. In that algorithm, axis vectors are defined as the fixed cluster centers, and hierarchical clustering in each sub-cluster is self-adaptive. These two clustering methods cooperate with each other in mate selection and environmental selection to handle MOPs with irregular PFs.

Clustering based approaches are attractive since they can automatically identify the distribution of the population and perform appropriate partitioning for dynamically defining reference vectors. It is worth noting, however, that the computational complexity of some clustering algorithms may be high, especially when dealing with MaOPs.

Grid or clustering based MOEAs are listed in Table SIV of the Supplementary material.

E. Discussions

The four categories of MOEAs for handling MOPs with irregular PFs have their own advantages and disadvantages. In the following, we provide some general guidelines for how to choose a most suitable algorithm for solving a given problem.

Using a set of fixed reference vectors to guide the search is helpful for exploitation and acceleration of convergence.However, a predefined fixed set of reference vectors is not suitable for a problem in which a very small proportion of reference vectors are active, such as MOPs with degenerate PFs. Because in these problems, most reference vectors are inactive, and a small number of active reference vectors cannot decompose the MOP properly. Moreover, a large number of invalid reference vectors waste computation resources.

When using the reference vector adjustment methods,attention should be paid to the convexity of the PF. It is recommended that a set of reference vectors with the ideal point as the origin for the concave PF and a reference vector set with the nadir point as the origin for the convex PF help improve the uniformity of population distribution. When the convexity of the PF is unknown, using the two sets of reference vectors simultaneously might be helpful.

The current methods for adjusting reference vectors or reference points are mostly based on the distribution of the current population, and such methods lack predictability. We suggest to analyze the non-dominated solutions during the optimization to predict the possible distribution of PF, which is helpful for adjusting the reference vectors or points. In the early stage of evolutionary search, more exploration should be maintained to make prediction more accurate. Machine learning may be a promising tool to perform the analysis and prediction.

In reference vector or point adjustment methods, the timing and methods for adjusting the reference vectors and points are important. If the adjustment frequency is too high, it is very likely to slow down the evolution speed, while if it is too low,it can happen that solutions in a promising area will get lost.We recommend to set up an external archive to store nondominated solutions that are not in the currently searched area.We also suggest to explore as many areas as possible before finding out the distribution of the PF. When the basic distribution of PF is detected, it is necessary to increase the selection pressure so that the population can quickly converge to the PF.

When using a grid-based method, we should pay special attention to the density of the grid and ensure that the boundary individuals are properly distributed in the grid. It is better to perform non-dominated sorting before using the grid-based method to avoid getting trapped in a local optimum. When the population distribution is relatively scattered, building a grid system with multiple regions can be helpful to reduce invalid grids.

Finally, clustering is an effective approach to irregular PFs,although both the connection criterion and distance measurement may influence the performance of clustering. Most algorithms do the clustering based on the current population,which is however easily affected by the dominated individuals in the evolutionary process. It is thus recommended to take both previous solutions and the individuals in the current population into account to achieve a good balance between convergence and adaptation.

V. FUTURE WORK

Although existing MOEAs have achieved great success in solving multi- and many-objective problems with irregular PFs, several challenges remain open.

1) Most of the existing MOEAs are designed for a certain type of irregular problems, and as a result, they can only solve one or a few types of irregular problems efficiently. Algorithms that can solve a widely range of irregular as well as regular MOPs are yet to be developed.

2) In addition to efficient adaptation of the reference vectors or reference points, more attention should be paid to generating candidate solutions in promising regions. It is conceivable that the search performance can be significantly enhanced by properly coordinating the guided generation of the offspring and adaptation of the reference vectors.

3) The performance of most existing MOEAs degenerates dramatically on large-scale MOPs [104]. So far little work has been done for large-scale MOPs or MaOPs with irregular Pareto fronts, and solving these problems will be more challenging since many existing methods for adapting the reference vectors may suffer from the curse of dimensionality.

4) MOPs with irregular Pareto fronts will become harder to solve if the Pareto fronts change over time, i.e., if the MOPs are dynamic [105]. In this case, the PFs may change over time, in terms of both the location, the shape as well as the nature of irregularity.

5) Solving expensive MOPs or MaOPs with irregular Pareto fronts is an extremely challenging topic since only a small number of evaluations of the objective functions can be afforded. In this case, more efficient adaptation methods are called for that can properly identify the distribution of Pareto fronts with a limited computational budget. Surrogate assisted evolutionary algorithms [106], [107] will be helpful, although surrogate model management in the presence of irregular Pareto fronts needs more research efforts.

In general, handling complex irregular MOPs requires a closer integration of evolutionary optimization and machine learning techniques, in particular unsupervised learning such as clustering, generative adversarial networks [108], and selforganizing neural networks. In case expensive optimization problems are involved, supervised, semi-supervised learning[109], [110], and transfer learning [111] will play a more important role.

VI. CONCLUSION

This paper provides a survey of methods for handling multiand many-objective optimization problems with irregular Pareto fronts. After introducing the basic concepts, elaborating the causes of the irregularity in the Pareto fronts, and discussing the main ideas of dealing with the irregular Pareto fronts together with their limitations, we outline the main remaining challenges that need to be addressed in the future.

We expect that evolutionary algorithms will play an increasingly important role in solving practical optimization problems in a wide range of science and engineering, many of which may have irregular Pareto fronts. Thus, we hope this survey paper is helpful to further promote the research activities in this area by providing in-depth understanding and useful insights into the problems, and triggering valuable inspirations for developing more efficient algorithms for solving challenging multi-objective optimization problems.