处理NaCs光解离问题的两种方案比较

张彩霞，岳大光，孟庆田

(山东师范大学物理与电子科学学院，济南 250014)

处理NaCs光解离问题的两种方案比较

张彩霞，岳大光，孟庆田

(山东师范大学物理与电子科学学院，济南 250014)

利用含时波包动力学方法中的劈裂算符-傅里叶变换传播方案和切比雪夫多项式展开方案研究了NaCs分子的光吸收截面，并对由这两种方案计算得出的结果进行了比较. 结果表明劈裂算符-傅立叶变换传播方案能更好地展示光吸收截面的中间动力学信息，而在研究初始波包与光吸收截面的关系时，由切比雪夫多项式展开方案获得的结果则更直观. 利用后一方案计算的从基态X1∑+不同振动态跃迁到激发态B1∑+上相应的光吸收截面的结果表明，初始波包对光吸收截面有一定的影响，所有振动态的吸收截面均表现出谐振行为，即每一个振动态吸收截面最小值的个数恰好等于基态振动态波函数节点的个数，这种节点映射行为与映射原理相符合.

光解离动力学; 光吸收截面; 含时波包法

1 引 言

光解反应动力学是分子反应动力学的一个重要分支，它主要研究分子吸收光子后发生分解反应产生光解碎片的过程以及光解碎片的内能分布和空间分布. 作为分子碰撞反应的半过程，光解反应能够使人们对电子与核之间的运动有一个更深的了解，从而获得反应物初态和产物终态的详细信息，这对于态-态分辨的分子反应动力学研究具有重要的指导意义. 另外，光解反应动力学的研究涉及到基元化学反应的核心问题，即化学键的断裂和生成，因此对光解过程的研究可以帮助我们理解分子断键过程的机理，从而更好地实现外场对化学反应的控制[1,2]. 在人们首次探测到光解碎片的内能分布并开创了光解反应动力学这一崭新学科以来，随着激光与分子束技术的发展，在过去的几十年里光解反应动力学取得了巨大的发展[3]，有关它的研究深入到了物理化学的各个领域，包括环境化学、团簇化学、大气化学以及量子散射理论等[1]. 二十世纪九十年代初，高分辨的H原子里德堡时间飞渡光谱仪的发展使光解反应动力学又有了新的发展[4]，即实现了光解碎片平动能分布的精确测量和光解碎片内能分布 (包括碎片的振动能分布及转动能分布) 的精准预测. 近年来随着现代实验手段的进步，光解动力学也得到了进一步的发展，研究者们把越来越多的精力集中在利用激光控制其反应方面.

异核冷分子由于具有永久电偶极矩和可调谐的长程各向异性偶极-偶极相互作用等特点，近些年越来越受到理论和实验研究者的关注. 冷分子的光解离动力学中包含了很多基态和激发态的信息，例如解离能、势阱的宽度和深度、势能面的形状等，所以对于冷分子的光解离动力学的研究显得尤为重要. 迄今为止，科学家们已经成功研究了许多冷分子的光解离. 1986年，A. Sharma 等人[5]首次对NaCs分子进行了光解离实验；紧接着这些人又对NaRb分子进行了激光诱导解离的研究[6]; 2011年A. Grochola 等人[7]对LiCs的解离机制进行了实验研究，即把基态的LiCs分子解离成原子Li(22S)和Cs(52D)；近年来，科学家则把更多的注意力放在了冷分子的光缔合研究上[8-10]. 而在两步光缔合过程的研究中，光解离也是一个关键的过程，这也促进了冷分子光解离动力学研究的进一步发展.

在对光解离过程的理论研究中，人们经常用到的方法包括经典轨线方法、准经典轨线方法、非含时波包方法和含时波包方法[11]. 其中含时波包法是一种研究光解离动力学的重要方法，这种方法的优势不仅表现在具有数值计算的高效性，同时它还为动力学提供了物理意义明确而直观的图像，它既具有经典的直观，又不乏量子力学的准确，许多研究成果已经证明了其在处理光与物质相互作用时的可行性[12-14]. 在处理波包的演化时，劈裂算符-傅里叶变换传播方案和切比雪夫多项式展开方案是研究者们常用的两种方案[15,16].切比雪夫多项式展开方案在波函数传播时采用比较长的时间步长，这使得该方法不仅具有计算效率高的优点，而且在研究与时间相关的动力学问题时也比较直观，但较长的时间步长也会导致动力学计算时中间信息的丢失，所以在需要得到动力学的一些详细信息时，这种方法是有缺陷的；劈裂算符-傅里叶变换传播方案则由于其在波函数传播时采用较小的时间步长，因此可以获得较详细的动力学信息，这样就可以弥补切比雪夫多项式展开方案的不足，且又由于其具有明确的演化算符使得该计算也容易进行[17].

在所有的碱金属双原子分子中，NaCs分子不仅是典型的冷分子，而且它还具有最大可测的偶极矩[8]，所以成为本工作的首选. 本文介绍了量子波包方法的理论模型，即求解初始波包时所用的傅立叶网格哈密顿方法，波包演化时所用的劈裂算符-傅里叶变换传播方案和切比雪夫多项式展开方案以及光吸收截面的计算方法等. 为了使对冷分子光吸收截面的理论计算有更深入的了解，以便根据具体的研究目标更好的选择传播方案，我们采用了两种方案即劈裂算符-傅里叶变换传播方案和切比雪夫多项式展开方案对NaCs分子的光吸收截面进行了理论计算，并对由这两种计算所得出的结果进行了比较；利用切比雪夫多项式展开方案计算从基态X1∑+不同振动态跃迁到激发态B1∑+上相应的光吸收截面也在本文给出.

2 理论简介

2.1 傅立叶网格哈密顿(Fourier grid Hamiltonian, FGH)方法

在坐标空间中，使用傅里叶变换方法，哈密顿算符的矩阵元可以写成如下形式

(1)

其中，核间距用r表示，动能算符和势能算符分别用Tk和V(r)表示. 将连续的坐标值采用离散的坐标格点rα=αΔr进行替代(这里的α为整数)，令N=2n+1，那么在动量空间中有

(2)

且某个点的动量值为

kn=nΔk-kmin，

(3)

(4)

和

(5)

离散化的哈密顿量可以写为[18,19]

(6)

其中

(7)

m表示约化质量. 将式(6)直接对角化就能得到本征值和本征函数. 这里的Δr表示权重因子，其可以保证所得本征函数归一化.

2.2 波包传播方案

2.2.1 劈裂算符-傅里叶变换传播方案

对于一个具有两个势能面的体系，在玻恩-奥本海默(Born-Oppenheimer，B-O)近似下，并且忽略转动态与其它自由度的耦合，体系的径向含时薛定谔方程可以写为如下形式：

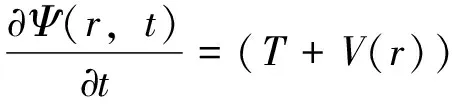
(8)

这里的Ψ(r,t)表示含时核的波函数，T、V(r)同上，它们分别可以表示为如下形式：

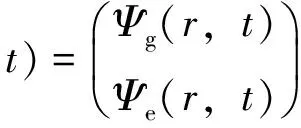
(9)

(10)

这里的Vg和Ve分别表示基态和激发态的绝热势，而Wge=Weg=Vge+μ(r)E(t)，Vge是两势能面的非绝热耦合势，μ(r)表示跃迁偶极矩，在式(9)中，Ψg和Ψe分别表示基态和激发态核的含时波函数.

给出初始时刻t0的波函数为Ψ(r,t0)，只考虑很小的时间间隔Δt，方程(8)的二级近似解就可以写为[20]

(11)

其中新的演化算符—动能演化算符UT和势能演化算符UV分别可以表示为如下形式

(12)

当时间传播n步后，得到经过时间演变后的波函数，如下所示[20]

(13)

2.2.2 切比雪夫多项式展开方案

通过FGH方法，可以得到当分子处在基电子态的一个束缚振动能级时的波函数Ψg(r,t0)，当处于该态的粒子吸收一个光子到达激发态时，此时获得该体系进行演化时的初始波包并由下式表示

Ψ(r,t0)=μ(r)Ψg(r,t0)，

(14)

(15)

这里的αn是多项式的展开系数，Pn是多项式的展开基. 这样就将波函数随时间的指数演化问题转换为利用多项式近似的演化问题.

考虑到切比雪夫多项式的取值范围为[-i,i]，所以为了使波函数归一化需要使哈密顿算符除以ΔE，同时为了使所计算的结果更加准确且本征值范围在[-1,1]内，那么哈密顿算符就需要变为[16]

(16)

其中ΔE=Emax-Emin，而Emin=Vmin，Emax=Vmax+Tmax，因此波函数的时间演化算符可以表示为

(17)

那么通过演化，波函数可以由下式进行描述[16]

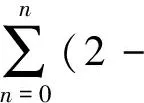
(18)

2.3 波函数的吸收

在对体系的波函数进行计算时，由于采用有限的基矢和格点，波函数传播到格点末端时会引起反射，从而造成动力学结果的不准确[21]. 为了消除这种边界反射，最直接有效的办法就是引入光学吸收势，这种方法已广泛应用到含时量子计算当中. 在本文中我们采用的吸收势形式如下[22]

(19)

这里的Vi0表示吸收势的高度，Rabs表示吸收势的位置，它必须远离相互作用区，而ΔRabs表示吸收势的宽度. 当波包传播到吸收区时，它的强度将逐渐变弱，最终在到达格点末端时，被吸收势完全吸收掉.

利用传播后的波函数给出光解过程的光吸收截面，即[23]

(20)

其中c是光速，ε0是真空介电常数，m同上，而ω和E分别是光子的角频率和分子的能量. 通道i的波函数Ψi和波矢ki则可以表示成如下形式

(21)

(22)

(22)式中的Vi(Rf)则代表在通道i，R=Rf(这里的Rf表示参考点的位置)时体系的势能.

3 计算结果与讨论

3.1 NaCs分子的光吸收截面

本文采用M. Aymar和O. Dulieu在文献 [24] 给出的NaCs分子基态X1∑+和激发态B1∑+的势能面(Potential Energy Curves, PECs)，如图1所示. 从图1中可以看出激发态B1∑+是一个排斥势，这样的势能面在满足一定的条件时很容易使分子发生解离，且该体系的解离能为0.1094 a u. 利用该势能面本文研究了该体系的光吸收截面.

图1 NaCs分子的势能面Fig. 1 The PECs for NaCs

为方便对光吸收截面的不同计算方案进行比较，这里分别采用劈裂算符-傅里叶变换传播方案和切比雪夫多项式展开方案研究了NaCs分子解离通道B1∑+上的吸收截面，如图2所示. 光吸收截面能够展示体系的振动能级结构[15]，它的最高峰所对应的光子能量代表光子被吸收的最可几能量，展宽代表光子能被吸收的能量范围. 从图2中可以看到由劈裂算符-傅里叶变换传播方案计算的光吸收截面的最可几能量相对于由切比雪夫多项式展开方案所计算出的最可几能量有一定的偏移，这是由于前一种方案中涉及到了外场，而外场与势能面的相互作用，可以使势能面被修饰，从而导致势能面之间的间隔发生变化，同时解离能也发生变化. 这种对势能面的修饰也能使吸收截面的带宽发生变化，特别是由于受弗兰克康登因子的影响，原来能被吸收的具有某一能量的光子现在变的不能再被吸收，或是被吸收的概率变小了，所以图2(a)的带宽明显要比图2(b)的小. 还有一个很明显的特征就是图2(a)中的光吸收截面不只有一个峰. 正如前面所说，劈裂算符-傅里叶变换传播方案涉及到外场效应，任一时刻的波函数都受基态和激发态势能面的影响，即与粒子的跃迁有关，所以所计算的光吸收截面能够反映基态势能面的某些信息. 从图2(a)中能够看到，在一个宽的包络里包含着一些窄的窗共振，这些窗共振的振幅大小能够反映基态势能面相应的各个振动能级的粒子数布居. 而切比雪夫展开方案不涉及外场效应，它的波函数的传播只受激发态势能面的控制，因此该方案所计算出的光吸收截面不能反映基态势能面各个振动态的粒子数布居信息. 从图1中可以看到，激发态是一个排斥势，波函数在该势能面上传播时不涉及在势阱中的振荡问题，所以当初始波函数取基态振动态v″=0的波函数时，由该方案获得的光吸收截面，如图2(b)所示，是一个光滑的近似对称的包络.

图 2 图(a)是由劈裂算符-傅里叶变换传播方案计算的在条件λ=385 nm，I=8×1012 W/cm2下，解离通道B1∑+上的光吸收截面；图(b)是由切比雪夫多项式展开方案计算的解离通道B1∑+上的光吸收截面Fig. 2 (a) The photoabsorption cross section in the channel B1∑+ at laser wavelength λ=385 nm and intensity I=8×1012 W/cm2 by using the split operator-Fourier transform propagation scheme; (b) The photoabsorption cross section in the channel B1∑+ by using the Chebyshev polynomial expansion scheme

3.2 NaCs分子从基态X1∑+的不同振动态跃迁到激发态B1∑+上的相应的光吸收截面

在研究不同初始波包对光吸收截面的影响时，本文选取三个不同振动态(v″=0，1，2)的波函数作为初始波包，并利用切比雪夫多项式展开方案计算了解离通道B1∑+上的光吸收截面. 从图3中可以看出，随着振动量子数v″的增加，解离通道B1∑+上的光吸收截面所拥有的峰数增加，这可能与初始波函数的形状有关. 从图3中还可以看出，随着v″的增加，光解截面的最大纵坐标即峰值减小，而光解离截面的整个包络的宽度却增加. 我们认为造成这种结果的原因是，由该种方案计算的光吸收截面能反映初始波包所在的振动态的粒子数，而v″越大，该振动态的粒子数越小，因此光吸收截面的峰值减小. 又由于初始波包所在的位置与激发态势能面之间的间隔随着v″的增大而减小，且初始波包在基态时的势阱振荡范围随v″的增大而增大，从而导致光解截面的最可几能量减小，而光解离截面的整个包络的宽度增加. 图4表示由FGH方法计算的基态X1∑+的不同振动态(v″=0，1，2)所对应的初始波函数.

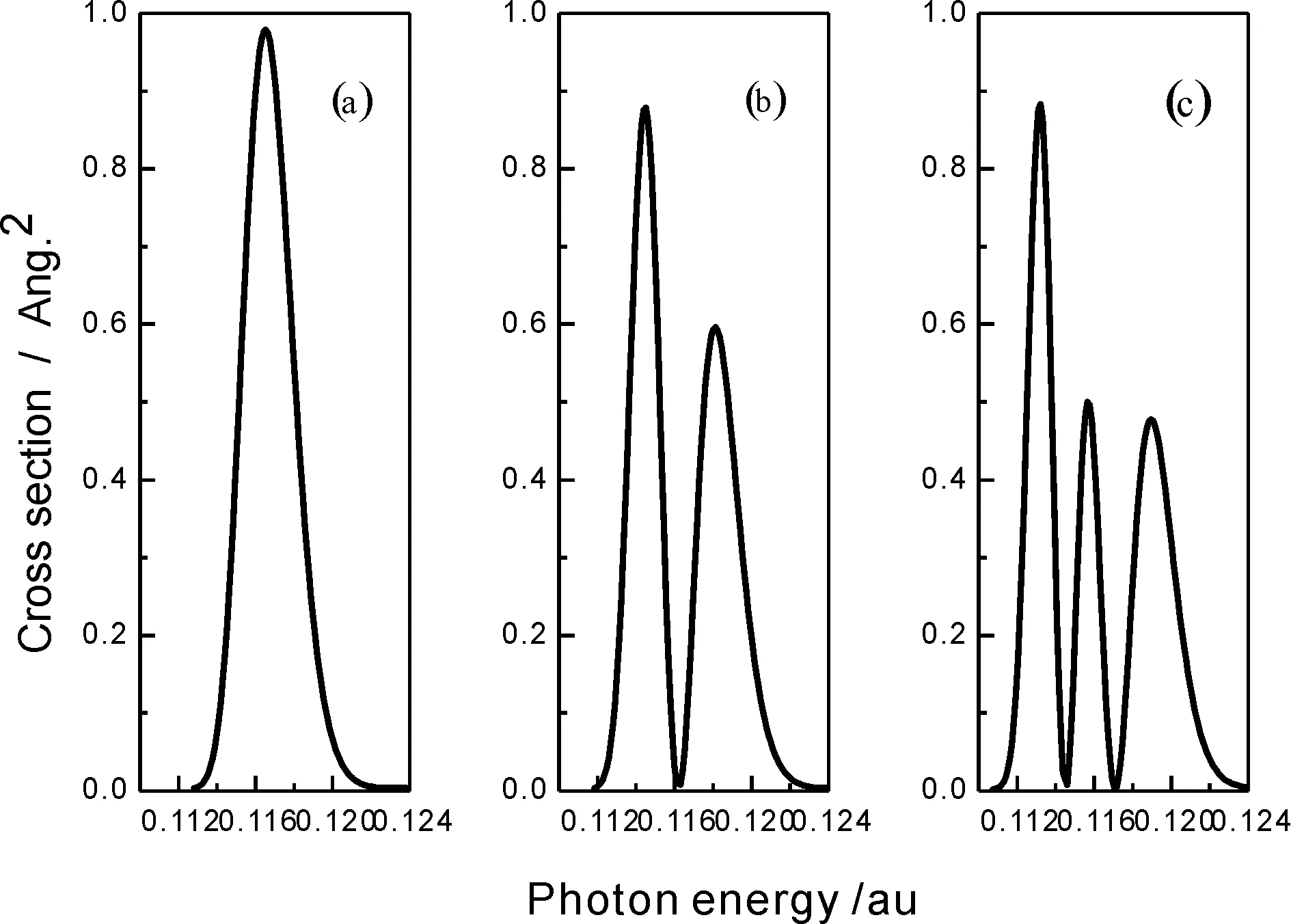
图3 (a)、(b)、(c)分别表示由切比雪夫多项式展开方案计算的从基态X1∑+不同振动态 (v″=0，1，2) 跃迁到激发态B1∑+上的所对应的光吸收截面Fig. 3 (a), (b) and (c) denote the photoabsorption cross section in the channel B1∑+ corresponding to the vibrational states v″=0，1，2, respectively, by using the Chebyshev polynomial expansion scheme

图4 (a)、(b)、(c)分别表示由FGH方法计算的基态X1∑+的不同振动态(v″=0，1，2)所对应的初始波函数Fig. 4 (a), (b) and (c) denote the initial wave function corresponding to the vibrational states v″=0，1，2 for the ground state X1∑+ by using FGH scheme

通过对比图3和图4可以看出，每个振动态的光吸收截面的最小值(除两端)个数等于基态束缚态各振动能级上波函数节点的个数，也就是说，v″=0时，初始波函数没有节点，且吸收截面也没有相应的最小值；而当v″=1时，初始波函数有一个节点，且吸收截面有一个最小值；v″=2时的行为如此类推. 这是由于在初始波函数的节点位置，粒子在该处的分布几率为零，从而导致具有相应能量的光子被吸收的概率为零. 这些振动态的光吸收截面所表现出来的这种谐振行为与映射原理[25]一致，即对应基态波函数的节点映射.

4 结 论

本文利用含时波包动力学理论研究了NaCs分子的光吸收截面. 在对波包进行传播时，分别采用了劈裂算符-傅里叶变换传播方案和切比雪夫多项式展开方案. 研究表明，由于这两种方案本身的差异，切比雪夫多项式展开方案无法较为详细地展示动力学过程中的某些信息，而劈裂算符-傅里叶变换传播方案则能弥补这一不足. 同时劈裂算符-傅里叶变换传播方案涉及到外场效应，而这种外场与体系的相互作用可以使电子态的势能面发生变化，从而使光吸收截面的中心和展宽发生变化. 所以在选取体系光吸收截面的计算方案时应视所研究的具体目标酌情而定. 利用切比雪夫多项式展开方案对从基态X1∑+不同振动态跃迁到激发态B1∑+上相应的光吸收截面的计算结果表明，初始波函数对光吸收截面有一定的影响，每个振动态所对应的光吸收截面的最小值个数与其基态束缚态各振动能级上波函数的节点个数相等，且光子被吸收的最可几能量和光吸收截面的展宽随着基振动态量子数v″的变化而变化. 这些振动态的光吸收截面所表现出来的谐振行为是基态波函数的节点映射，符合映射原理.

[1] Butler L J, Neumark D M. Photodissociation dynamics [J].J.Phys.Chem., 1996, 100 (31): 12801.

[2] Lei Z Z, Liu J, Zhou X Y,etal. Photodissociation of Cs2molecules and collisional energy transfer [J].J.At.Mol.Phys., 2004, 21 (1): 23(in Chinese)[雷振宙, 刘静, 周小岩, 等. Cs2分子的光解离和碰撞能量转移[J]. 原子与分子物理学报, 2004, 21 (1): 23]

[3] Zhao M Y.Theoreticalstudiesofphotodissociationdynamicsfortriatomicmolecules[D]. Dalian: Dalian Institute of Chemical Physics, Chinese Academy of Sciences, 2005 (in Chinese) [ 赵美玉. 三原子分子光解动力学的理论研究[D]. 大连：中国科学院大连化学物理研究所, 2005]

[4] Schnieder L, Meier W, Welge K H,etal. Photodissociation dynamics of H2S at 121.6 nm and a determination of the potential energy function of SH(A2∑+) [J].J.Chem.Phys., 1990, 92 (12): 7027.

[5] Sharma A, Dixit M N, Bhale G L. Relative photodissociation cross-section of NaCs molecule, using argon ion laser lines [J].J.Phys., 1986, 27 (5): 695.

[6] Sharma A, Bhale G I, Razvi M A N,etal. Laser induced photodissociation of the NaRb molecule [J].Opt.Commun., 1987, 61 (1): 21.

[7] Grochola A, Szczepkowski J, Jastrzebski W,etal. Experimental investigation of electronic states of LiCs dissociating to Li(22S) and Cs(52D) atoms [J].J.Chem.Phys., 2011, 135 (4): 044318.

[8] Zhang C Z, Zheng B, Wang J,etal. Theoretical simulation of the photoassociation process for NaCs [J].Chin.Phys. B, 2013, 22 (2): 023401.

[9] Zhao Z Y, Zhang W, Huang Y,etal. Photoassociation dynamics controlled by a spectral π-jump laser pulse [J].LaserPhys., 2013, 23 (3): 035502.

[10] Zhang H S, Ji Z H, Yuan J P,etal. Cold cesium molecules produced directly in a magneto-optical trap [J].Chin.Phys. B, 2011, 20 (12): 123702.

[11] Schinke R.Photodissociationdynamics[M]. Cambridge: Cambridge University Press, 1993.

[12] Meng Q T, Yang G H, Sun H L,etal. Theoretical study of the femtosecond -resolved photoelectron spectrum of the NO molecule [J].Phys.Rev. A, 2003, 67 (6): 063202.

[13] Meng Q T, Liu C H, Zhang Q G,etal. Time-dependent wavepacket dynamical approach to intense field effect of multiphoton ionization for diatomic molecules [J].J.At.Mol.Phys., 2006, 23 (2): 241(in Chinese)[孟庆田, 刘春华, 张庆刚, 等. 双原子分子多光子电离强场效应的含时波包动力学研究[J]. 原子与分子物理学报, 2006, 23 (2): 241]

[14] Lu R F, Zhang P Y, Han K L. Attosecond-resolution quantum dynamics calculations for atoms and molecules in strong laser fields [J].Phys.Rev. E, 2008, 77 (6): 066701.

[15] Meng Q T, Varandas A J C. Manifestation of external field effect in time-resolved photo-dissociation dynamics of LiF [J].Chin.Phys. B, 2013, 22 (7): 073303.

[16] Bhattacharjee A, Dastidar K R. Photodissociation of NaH [J].Phys.Rev. A, 2002, 65 (2): 022701.

[17] Zhao M Y, Meng Q T, Xie T X,etal. Nonadiabatic photodissociation dynamics [J].Int.J.Quantum.Chem., 2005, 101 (2): 153.

[18] Marston C C, Balint-Kurti G G. The Fourier grid Hamiltonian method for bound state eigenvalues and eigenfunctions [J].J.Chem.Phys., 1989, 91 (6): 3571.

[19] Balint-Kurti G G, Dixon R N, Marston C C. Grid methods for solving the Schrödinger equation and time dependent quantum dynamics of molecular photofragmentation and reactive scattering processes [J].Int.Rev.Phys.Chem., 1992, 11 (2): 317.

[20] Feit M D, Fleck J A, Steiger A. Solution of the Schrö-dinger equation by a spectral method [J].J.Comput.Phys., 1982, 47 (3): 412.

[21] Neuhasuer D, Baer M. The time-dependent Schrödinger equation: Application of absorbing boundary conditions [J].J.Chem.Phys., 1989, 90 (8): 4351.

[22] Feuerstein B, Thumm U. Fragmentation of H+2in strong 800-nm laser pulses: Initial-vibrational-state dependence [J].Phys.Rev. A, 2003, 67 (4): 043405.

[23] Alekseyev A B, Liebermann H P, Buenker R J,etal. Spin-orbit effects in photodissociation of sodium iodide [J].J.Chem.Phys., 2000, 113 (4): 1514.

[24] Aymar M, Dulieu O. Calculations of transition and permanent dipole moments of heteronuclear alkali dimers NaK, NaRb and NaCs [J].Mol.Phys., 2007, 105 (11-12): 1733.

[25] Brown A, Balint-Kurti G G. Spin-orbit branching in the photodissociation of HF and DF. II. A time-dependent wave packet study of vibrationally mediated photodissociation [J].J.Chem.Phys., 2000, 113 (5): 1879.

Comparison of two schemes for investigating NaCs photodissociation

ZHANG Cai-Xia, YUE Da-Guang, MENG Qing-Tian

(College of Physics and Electronics, Shandong Normal University, Jinan 250014, China)

The present work investigates the photoabsorption cross section of NaCs by using the split operator-Fourier transform propagation scheme and the Chebyshev polynomial expansion scheme. The comparison of the two calculated results shows that the split operator scheme can better exhibit the intermediate results of the dynamics process, while the other scheme is hard to satisfy this requirement due to the long time step. In this paper the photoabsorption cross sections, corresponding to the wave packet of the different vibrational states in the ground state transited to the excited states, also are calculated. The results show that the initial wave packet has a certain impact on photoabsorption cross section. The photoabsorption cross section corresponding to the related vibrational state shows a resonant behavior, i.e. the number of the minimum of the cross section corresponding to the each vibrational state is exactly equal to the number of the node of the wave function in the ground vibrational state. This situation caused by the reflection of the wave packet is accordance with the well-known reflection principle.

Photodissociation dynamics； Photoabsorption cross section； Time-dependent wave packet method

国家自然科学基金(11074151)；2012年高等学校博士学科点专项科研基金(20123704110002)

张彩霞(1987—), 女，汉族，山西原平人，主要从事外场与原子、分子的相互作用.E-mail: zhangcx298@126.com

孟庆田.E-mail: qtmeng@sdnu.edu.cn

103969/j.issn.1000-0364.2015.08.001

O561.4

A

1000-0364(2015)08-0531-07

投稿日期:2014-08-31