具有Eckart势的Schrödinger方程的任意l波解析解

安 博

(1.渭南师范学院物理与电气工程学院物理系，渭南 714099; 2.陕西省X射线检测与应用研究开发中心, 渭南 714099)

具有Eckart势的Schrödinger方程的任意l波解析解

安 博1, 2

(1.渭南师范学院物理与电气工程学院物理系，渭南 714099; 2.陕西省X射线检测与应用研究开发中心, 渭南 714099)

Eckart势； 完全量子化规则； Greene-Aldrich近似

1 引 言

由于精确解包含了几乎所有的量子信息，所以其在量子计算中具有非常重要的作用，但是只有极少简单的量子系统具有精确解．目前人们已经发展了许多寻找精确解的有效方法，如：因式分解[1]、超对称[2,3]、分离变量[4]和SWKB[5]等方法，解决了如Pöschl-Teller势[6]、双环状振子势[7]、Makarov势[8]、类Quesne环状球谐振子势[9]等物理模型．

Eckart势作为量子力学中一个重要的指数型可解势，首先于1930年被Eckart[9]提出．由于其在物理[10]和化学物理[11]方面的广泛应用，研究者探讨了具有Eckart势的Schrödinger方程、Klien-Gordon方程和Dirac方程的基态解[12-14]．但这些研究都被限制在方程的s波解．在上述研究基础上，本文提出采用Greene-Aldrich法对离心项近似，使用完全量子化规则计算了具有离心项的Eckart势的Schrödinger方程l(l≠0)波解析解，并分别讨论了基态和激发态下，势能范围参数λ和势阱深度η对具有不同角动量量子数的能量本征值的影响以及能量本征值和径向量子数n与角动量量子数l之间的关系．

2 完全量子化规则

一维Schrödinger方程可表示为：

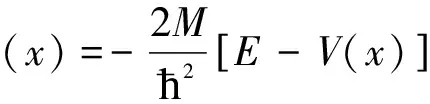
(1)

式(1)可以写成一个非线性Riccati方程：

φ(x)2

(2)

(3)

(4)

上式第二项可表示为：

π

(5)

将其代入式(3)得到：

π=nπ

(6)

若在三维空间中式(6)可表示为：

π

(7)

方程(6)和(7)被称作完全量子化规则[17-20]．

3 Eckart势的l波解析解

三维空间中Eckart势表示为[9]：

(8)

(9)

为简化表达式，做以下变量替换：

V2=λ2δ，V1=λ2γ

(10)

式(9)可另写为：

V(r)=V2y2+V1y

(11)

通过解方程Enl=V(r)得到两个转折点的关系：

(12)

将新变量代入基态非线性Riccati方程(2)得：(为简单下面选取自然单位ħ2=M=1)

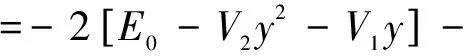
(13)

由于基态φ0(r)只有一个零点且无极点，则其一定是y的线性函数，根据Sturm-Liouville定理[17]，令φ0(r)=C1y+C2(C1>0)，代入式(13)得：

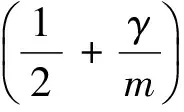
(14)

波矢k(r)可表示为：

将其代入式(7)的第一个积分中，得：

(15)

用E0替代式(15)中的Enl，得：

(16)

根据完全量子化规则，将式(15)和(16)代入式(7)，得：

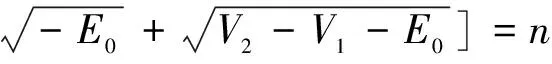
(17)

其解为：

(18)

为进一步研究能谱性质，图1(a)和(b)分别表示基态(n=0)和激发态(n=1)具有不同角动量量子数的能量本征值和势能范围参数λ之间的关系．可以看出，当l=0时能量曲线被强烈束缚在一个λ相对较宽的范围内，随着l增大，能量的束缚范围越来越小，尤其当l=10时，能量被束缚在一个λ相对极小的范围内，此时引力势程较短．总言之，随自旋量子数l的增大，能量被束缚的范围变小，l导致能量对λ变化敏感，因此λ的选择具有极小范围．图2(a)和(b)分别表示基态和激发态具有不同角动量量子数的能量本征值和势阱深度η之间的关系．可以看出，随着势阱深度的增加，能量先増后减．图3表示能量随径向量子数n和角动量量子数l的变化关系．可以看出，具有相同l时，能量随n的增大而增大；具有相同n时，能量随l增大而增大．

图1 具有不同角动量量子数的能量本征值和λ之间的关系(σ=0.025，η=0.00005)(a) 基态(n=0)(b) 第一激发态(n=1)Fig. 1 The variations of energy eigenvalue for various values of l as a function of the λ (σ=0.025，η=0.00005)(a) ground state(n=0)(b) first excited state(n=1)

图2 具有不同角动量量子数的能量本征值和势阱深度η之间的关系(σ=η=0.025)(a) 基态(n=0)(b) 第一激发态(n=1)Fig. 2 The variations of energy eigenvalue for various values of l as a function of the η (σ=0.025，η=0.00005)(a) ground state(n=0)(b) first excited state(n=1)

图3 能量本征值与n和l之间的关系Fig. 3 Relations of n and l with energy eigenvalue

4 结 论

本文采用完全量子化规则和Greene-Aldrich近似法研究了具有离心项的Eckart势的Schrödinger方程，得到其任意l波解析解．讨论了势能范围参数和势阱深度对Eckart势基态和激发态能谱的影响，结果表明：(1) 随l增大，能量被束缚的范围变小，引力势程减小；(2) 随势阱深度增加，能量先增后减；(3)n和l增大引起能量本征值增大．

[1] Arcos-Olalla R, Reyes M A, Rosu H C. An alternative factorization of the quantum harmonic oscillator and two-parameter family of self-adjoint operators [J].Phys.Lett. A, 2012, 376: 2860.

[2] Chen G. Bound states of relativistic particles in Rosen-Morse potential [J].ActaPhys.Sin., 2004, 53(3): 680(in Chinese) [陈刚. Rosen-Morse势阱中相对论粒子的束缚态[J]. 物理学报, 2004, 53(3): 680]

[3] Zarrinkamar S, Rajabi A A, Hassanabadi H. Dirac equation for the harmonic scalar and vector potentials and linear plus coulomb-like tensor potential: the SUSY approach [J].AnnPhys., 2010, 325: 2522.

[4] Zhang J F, Xu C Z, He B G. The variable separation approach and study on solving the variable-coefficient nonlinear Schrödinger equation [J].ActaPhys.Sin., 2004, 53(11): 3652 (in Chinese)[张解放, 许昌智, 何宝钢. 变量分离法与变系数非线性薛定谔方程的求解探索 [J]. 物理学报, 2004, 53(11): 3652]

[5] Yin C, Cao Z Q, Shen Q S. Why SWKB approximation is exact for all SIPs [J].Ann.Phys., 2010, 325: 528.

[6] Jia C S, Chen T, Cui L G. Approximate analytical solutions of the Dirac equation with the generalized Pöschl-Teller potential including the pseudo-centrifugal term [J].Phys.Lett. A, 2009, 373: 1621.

[7] Chen C Y, You Y, Wang X H. Exact solutions of the Schrödinger equation with double ring-shaped oscillator [J].Phys.Lett. A, 2013, 377: 1521.

[8] Chen C Y, Liu C L, Lu F L. Exact solutions of Schrödinger equation for the Makarov potential [J].Phys.Lett. A, 2010, 374: 1346.

[9] Zhang M C. Quesne-like ring-shaped spherical harmonic oscillator potential and pseudospin symmetry [J].ActaPhys.Sin., 2009, 58(2): 712 (in Chinese)[张民仓. 类Quesne环状球谐振子势场中赝自旋对称性 [J]. 物理学报, 2009, 58(2): 712]

[9] Eckart C. The penetration of a potential barrier by electrons [J].Phys.Rev., 1930, 35(11): 1303.

[10] Cooper F, Khare A, Sukhatme U. Supersymmetry and quantum mechanics [J].Phys.Rep., 1995, 251: 267.

[11] Cimas A, Aschi M, Barrientos C. Computational study on the kinetics of the reaction of N(4S) with CH2F [J].Chem.Phys.Lett., 2003, 374(3): 594.

[12] Dong S H, Qiang W C, Sun G,etal. Analytical approximations to the l-wave solution of the Schrödinger equation with the Eckart potential [J].J.Phys. A:Math.Theor., 2007, 40(34): 10535.

[13] Zhang M C, Huang-Fu G Q. L2-series solutions of the Schrödinger equation with the Eckart potential [J].Phys.Scr., 2010, 82(6): 065012.

[15] Yi L Z, Diao Y F, Liu J Y,etal. Bound states of the Klein-Gordon equation with vector and scalar Rosen-Morse-type potentials [J].Phys.Lett. A, 2004, 333(3): 212.

[14] Zou X, Yi L Z, Jia C S. Bound states of the Dirac equation with vector and scalar Eckart potentials [J].Phys.Lett. A, 2005, 346(1): 54.

[15] Ma Z Q, Xu B W. Exact quantization rule and the invariant [J].ActaPhys.Sin., 2006, 55(4): 1571 (in Chinese) [马中琪, 许伯威. 精确的量子化条件和不变量 [J]. 物理学报, 2006, 55(4): 1571]

[16] Gu X Y, Dong S H, Ma Z Q. Energy spectra for modified Rosen-Morse potential solved by the exact quantization rule [J].J.Phys. A:Math.Theor., 2009, 42(3): 035303.

[17] Qiang W C, Dong S H. Proper quantization rule [J].Europhys.Lett., 2010, 89: 10003.

[18] Serrano F A, Gu X Y, Dong S H. Qiang-Dong proper quantization rule and its applications to exactly solvable quantum systems [J].J.Math.Phys., 2010, 51(8): 082103.

[19] Sameer M I, Jamal A H. Quantization rule solution to the Hulthén potential in arbitrary dimension with a new approximate scheme for the centrifugal term [J].Phys.Scr., 2011, 83(2): 025002.

[20] Serrano F A, Dong S H. Proper quantization rule approach to three-dimensional quantum dots [J].Quant.Chem., 2013, 113: 2282.

[21] Zhang M C, Huang-Fu G Q. Analytical approximation to the l-wave solutions of the Eckart potential in the tridiagonal representation [J].Phys.Scr., 2012, 85(1): 015005.

Analytical solution to the arbitraryl-wave bound state
of the Schrödinger equation for the Eckart potential

AN Bo1, 2

(1.Department of Physics, Weinan Normal University, Wei’nan 714099, China;2.Center of Ray Detection and Application of Shanxi, Wei’nan 714099, China)

The Schrödinger equation including Eckart potential with centrifuge term was investigated using the proper quantization rule approach for any states. Setting the proper quantization rule and using Greene-Aldrich approximation, the energy spectra of Eckart potential can be determined from its ground state energy only. Finally, we discussed (1) the influences of the range of potentialηand the depth of potentialλon, respectively, the ground and first excited states for variousl, and (2) the relations of radial quantum numbernand angular quantum numberlwith energy eigenvalue.

Eckart potential; Proper quantization rule; Greene-Aldrich approximation

2014-07-27

国家自然科学基金青年科学基金(11304230)；渭南师范学院特色学科建设项目(14TSXK06)

安博(1981—), 男，陕西省渭南市人，硕士，讲师，从事量子多体理论研究.E-mail: mranbo@126.com

103969/j.issn.1000-0364.2015.08.021

O431.1

A

1000-0364(2015)08-0643-04