基于频率调制激光驱动的囚禁离子几何相位逻辑门

王中结, 方 旭

(安徽师范大学物理与电子信息学院, 芜湖 241000)

基于频率调制激光驱动的囚禁离子几何相位逻辑门

王中结, 方 旭

(安徽师范大学物理与电子信息学院, 芜湖 241000)

为了避免激光相位的起伏对几何相位逻辑门保真度的影响，提出一种基于囚禁离子的量子几何相位逻辑门的新方案.该方案是利用一束频率调制的行波激光场作用于两个囚禁离子上实现的.它的优点有：操作简单，仅需一步就能实现，不灵敏于激光场的相位也不需要对囚禁离子进行个别寻址.

量子光学； 量子几何相位门； 囚禁离子； 频率调制

1 引 言

在过去几年中，量子几何相位逻辑门的研究在理论和实验上都取得了显著的进展[1-8].不同于量子动力学型的逻辑门，量子几何相位逻辑门的操作是基于系统全局几何相位的思想, 并被认为是能够实现内置的容错量子计算[9].到目前为止，人们已针对不同的系统提出了构建量子几何相位门的各种方案，如在囚禁离子系统[9]，核磁共振系统[10]，超导系统[11]，量子点系统[12]，等等.在囚禁离子系统中，量子相位逻辑门是通过两束激光作用在囚禁离子上实现的.这个机制的核心是通过激光驱动实现一种依赖于囚禁离子内态的振动模式位移算符的相互作用哈密顿，但这个机制非常灵敏于激光场的相位[13]. 文献[14]的作者提出了一种利用一束驻波激光场驱动囚禁离子从而实现量子几何相位门的方案.然而，这个机制不但要求激光的相位是可控的而且要求激光场的相位必须满足严格的条件.近来，Lemmer等人提出基于激光和微波混合驱动囚禁离子的量子几何相位门方案[15]，该方案有助于抑制去相噪声，从而提高量子门操作的保真度.此外，据作者所知，所有量子几何相位门在其工作期间都易受激光相位起伏的影响.

在本文中，我们提出一种量子几何相位门，该方案基于使用一束频率调制行波激光作用于囚禁离子上实现的.我们提出的方案非常简单，仅需一步操作就可实现.它不仅不需要对囚禁离子单独寻址而且对激光相位的起伏不敏感.

2 量子几何相位门

我们考虑N个能级差为ħωa的二能级离子被囚禁在一个简谐势阱中，用一束频率调制的行波激光作用于囚禁离子上，那么，系统的哈密顿可表示为 (令ħ=1)

H=H0+HI

(1)

(2)

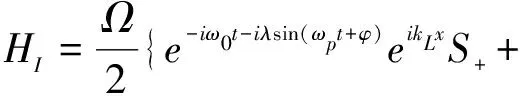
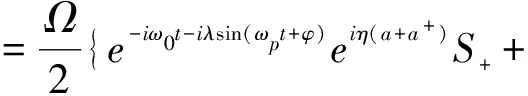
(3)

(4)

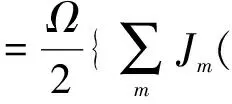
(5)

式中Δ=ωa-ω0是激光场载频和离子跃迁频率间失谐量，Jm(λ)是贝塞尔函数.在以下的分析中，我们选择失谐量Δ=0，于是我们可以得到在相互作用图像中相互作用哈密顿为

(6)

应用Lamb-Dicke近似，选择激光场的调制频率满足条件ν-ωp<<ωp,ν，并且忽略快速时变项，我们可以得到

HI(t)=iε0Sx+iεSx(ae-iδteiφ-a+eiδte-iφ)

(7)

式中δ=ν-ωp，ε0=ΩJ0(λ)/2，ε=ηΩJ1(λ)/2.根据位移算符的定义，在无限小的时间间隔[t,t+dt]，系统的演化算符可由下式确定

U(dt) =e-idtHI(t)

=e-idtε0Sxe[dαa+-dα*a]Sx

=e-itε0SxD(dαSx)

(8)

式中dα=-εeiδtdt.应用有关位移算符的公式

(9)

系统在相互作用时间t 的演化可以表示为[14]

α)

(10)

式中

(11)

α)=D(0)=1

(12)

于是，我们可以得到系统的演化算符为

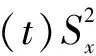
(13)

作为一个例子，我们考虑一个二比特的量子几何相位逻辑门的实现.用一束经典的频率调制的行波激光照射二囚禁离子上一段时间t，根据(13)式，系统的演化算符可表示为

U(t)=eiϑ(t)e-iφ(t)(σx1+σx2)

[cosϑ(t)+iσx1σx2sinϑ(t)]

(14)

选择σxi(i=1,2)的本征态矢 |±>i作为计算基矢，即σxi|±>i=±|±>i，我们可以得到下列态矢的演化

|++>12→e-i2φ(t)ei2ϑ(t)|++>12=eiθ1(t)|++>12

(15)

|+->12→|+->12

(16)

|-+>12→|-+>12

(17)

|-->12→ei2φ(t)ei2ϑ(t)|-->12=eiθ2(t)|++>12

(18)

式中 θ1(t)=2ϑ(t)-2φ(t)，θ2(t)=2ϑ(t)+2φ(t).明显看出这是一个量子几何相位门.例如，通过调节激光的调制振幅和拉比频率(与激光强度有关)满足θ1(t)=0，θ2(t)=π，我们可以得到一个π相位逻辑门.

3 讨论与结论

与以前人们提出的量子几何相位门方案相比[14]，本方案具有一些优点：(1)这种方法是非常简单的，因为它只需一步操作；(2)该方法只需要单个激光束，从而可避免的两个以上的激光束的准直调整；(3)在该方法中，相位逻辑门的操作由激光的调制频率和振幅，而不是由激光的相位进行控制，从而避免激光相位的起伏引起的误差；(4)该方法不要求对个别囚禁离子进行寻址.

总之，我们提出了一种基于囚禁离子与频率调制的行波光场的相互作用的量子几何相位门的方案.该方案具有操作简单抗退相干等优点.

[1]PachosJ,WaltherH.QuantumcomputationwithtrappedIonsinanopticalcavity[J]. Phys. Rev. Lett., 2002, 89(18): 187903.

[2]WuH,GaugerEM,GeorgeRE, et al.Geometricphasegateswithadiabaticcontrolinelectronspinresonance[J]. Phys. Rev.A, 2013, 87(3): 032326.

[3]EkertA,EricssonM,HaydenP, et al.Geometricquantumcomputation[J]. J. Mod. Opt., 2000, 47(14-15): 2501.

[4]ZhengSB.UnconventionalgeometricquantumphasegateswithacavityQEDsystem[J]. Phys. Rev.A, 2004, 70(5): 052320.

[5]PachosJK,BeigeA.Decoherence-freedynamicalandgeometricalentanglingphasegates[J]. Phys. Rev.A, 2004, 69(3): 033817.

[6]ZhuSL,WangZD.Unconventionalgeometricquantumcomputation[J]. Phys. Rev. Lett.，2003，91(18)： 187902.

[7]ChenCY,FengM,ZhangXL, et al.Strong-driving-assistedunconventionalgeometriclogicgateincavityQED[J]. Phys. Rev.A, 2006, 73: 032344.

[8]JiYH,CaiSH,LeJX.Operatingageometricquantumgatebyexternalcontrollableparameters[J]. Chin. Phys.B, 2010, 19(1): 010311.

[9]LeibfriedD,DeMarcoB,MeyerV, et al.Experimentaldemonstrationofarobust,high-fidelitygeometrictwoion-qubitphasegate[J]. Nature (London), 2003, 422: 412.

[10]JonesJA,VedralV,EkertA.Geometricquantumcomputationusingnuclearmagneticresonance[J]. Nature (London), 2000, 403: 869.

[11]FalciG,FazioR,PalmaGM, et al.Detectionofgeometricphasesinsuperconductingnanocircuits[J]. Nature(London), 2000, 407: 355.

[12]PuriS,KimNY,YamamotoY.Two-qubitgeometricphasegateforquantumdotspinsusingcavitypolaritonresonance[J]. Phys. Rev.B, 2012, 85(24): 241403R.

[13]HaljanPC,BrickmanK,DeslauriersL, et al.Spin-dependentforcesontrappedionsforphase-stablequantumgatesandentangledstatesofspinandmotion[J]. Phys. Rev. Lett., 2005, 94(15): 153602.

[14]ZhengSB.High-speedgeometricquantumphasegatesfortrappedionsinthermalmotion[J]. Phys. Rev.A, 2006, 74(3): 032322.

[15]LemmerA,BermudezA,PlenioMB.Drivengeometricphasegateswithtrappedions[J]. New Journal of Physics, 2013, 15(8): 083001.

A scheme for the geometric phase logic gates based on trapped ions driven by frequency-modulated laser

WANG Zhong-Jie, FANG Xu

(College of Physics and Electronic Information, Anhui Normal University, Wuhu 241000, China)

To avoid the effect of phase fluctuation of laser on fidelity of the geometric phase logic gate, we propose a scheme for quantum geometric phase gate based on trapped ions. This scheme works by the interaction of the trapped ions with a frequency-modulation traveling wave light field. The advantages of the scheme include: it can work by one-step operation, it is insensive to the phase of the laser, and it does not require individual addressing.

Quantum optics; Quantum geometric phase gates; Trapped ion; Frequency modulation

2014-02-04

安徽省自然科学基金资助项目(090412060)

王中结(1962—)，男，博士，教授，主要从事量子光学等领域的研究.E-mail: wuliwzj@mail.ahnu.edu.cn

103969/j.issn.1000-0364.2015.08.020

O431.2

A

1000-0364(2015)08-0640-03