LiBr分子基态光谱常数和分子常数研究

张金平，田 凯，李 慧，张洋洋

(黄河科技学院信息工程学院，郑州 450006)

LiBr分子基态光谱常数和分子常数研究

张金平，田 凯，李 慧，张洋洋

(黄河科技学院信息工程学院，郑州 450006)

采用高精度的量子化学从头计算多参考组态相互作用方法(MRCI)和相关一致基, 计算了LiBr分子基态的光谱常数(Re,ωeandDe)和势能曲线. 为获得更准确的结果, 计算中还考虑了二阶Douglas-Kroll-Hess相对论修正对LiBr分子基态的平衡键长、谐振频率和离解能影响. 将计算得到的势能曲线拟合为Murrell-Sorbie解析势能函数形式, 并进一步计算得到LiBr分子基态的其它光谱常数(ωeχe,αe,BeandD0). 比较发现它们与实验值符合的非常好. 通过求解核运动径向Schrödinger方程, 找到了LiBr分子基态的全部振动态. 还计算了每一个振动态的振动能级、经典转折点和惯性转动常数, 这些结果与已有的实验值一致.

光谱常数； 势能曲线； 分子常数； 相对论修正

1 Introduction

In the earliest days, alkali metal halides are of importance in quantum chemistry. They have played a central role in the understanding of the ionic bond[1]as well as in the development of the Landau-Zener method[2,3]for treating curve crossings. Recently, alkali metal halides also have important practical applications, from halogen metallurgy, chemical vapor transport and deposition[4-7]to the lamp industry. Among the alkali metal halides, LiBr molecule is one of the species which has received particular attention. A number of experimental[8-17]and theoretical[18-27]studies have been carried out about the LiBr molecule.

Around the 1950s, the experimental investigation of the LiBr molecule has been applied with the microwave spectroscopy technique[8]. Up until now, an increasing amount of interest has been paid to the comprehension of the properties of the LiBr molecule. However, it is important to mention that the spectroscopic constants of the LiBr molecule such as the harmonic frequencyωehave shown a wide variation[8-12, 16, 17]. And up to now, the accurate harmonic frequency has not been determined experimentally. On the theoretical front, these investigations[18-27]have focused mainly on the electronic structure and spectroscopic properties of the LiBr molecule potential in the equilibrium region. However, the extracted molecular parameters from these investigations are all incomplete. For example, we have found very little results about their vibrational levels, classical turning points and inertial rotation and centrifugal distortion constants, which are very useful in the theoretical rovibrational transition calculations.

The goal of the present work is to provide accurate harmonic frequencyωe, equilibrium internuclear distanceReand the potential energy curves (PECs) of the LiBr(X1∑+) molecule. Following, illustrate the relativistic scalar correction importance on the studied molecular properties. And the ab initio PECs are fitted to the analytical potential energy functions (APEFs) using a suitable Murrel-Sorbie (M-S) function. Based on the APEFs, the spectroscopic parameters and total vibrational manifolds are determined. The reliability of present theoretical method has been evaluated. The present results also provide more complete and accurate theoretical investigations on the molecular constants of LiBr molecule to this day.

2 Computational methods

All the calculations are made with the full valence complete active space self-consistent field (CASSCF) mothod[28]followed by the highly accurate valence internally contracted multireference configuration interaction (MRCI) approach[29, 30]. A full CI exactly solves the Schrödinger equation within some basis sets, but is usually too complex a calculation to compute molecules containing more electrons. The single reference methods can almost always be done, and usually are not very challenging (to the computer or the user), however, their accuracy is limited. MRCI is a way to systematically include those configuration state functions (CSFs) that contribute most significantly to the correlation energy[31]. It is precise in treating small systems, especially dimers.

The present calculations are performed with the MOLPRO 2008.1 package[32]. The one electron correlation-consistent basis set of Dunning and co-workers[33]is used throughout the present work. In particular, for the Li atom thespdfghcc-pV5Z basis set is employed, while for the Br atom the largest basis sets aug-cc-pV5Z are used, respectively. We believe that the very large basis sets, coupled with the effectiveness of the high-quality ab initio quantum chemical method MRCI procedure in treating the electron correlation, can give reliable harmonic frequencyωe, equilibrium internuclear distanceRe, dissociation energyDeand the PEC.

In general, the PECs calculations are made at intervals of 0.05 nm over the internuclear distance range from 0.08 to 2.07 nm. The ab initio results are all fitted to the Murrel-Sorbie (M-S) function with the least-squares fitting method. Thus the APEFs are derived, and then the rest spectroscopic parameters,ωeχe,αe,BeandD0, are determined. Based on the APEFs, the first 20 vibrational states are performed by solving radial Schrödinger equation of nuclear motion. And the complete vibrational levels, the classical turning points (RminandRmax), and the inertial rotation constants are reproduced whenJ= 0. All the calculations are carried out on our supercomputer Dawning TC4000A.

3 Results and discussion

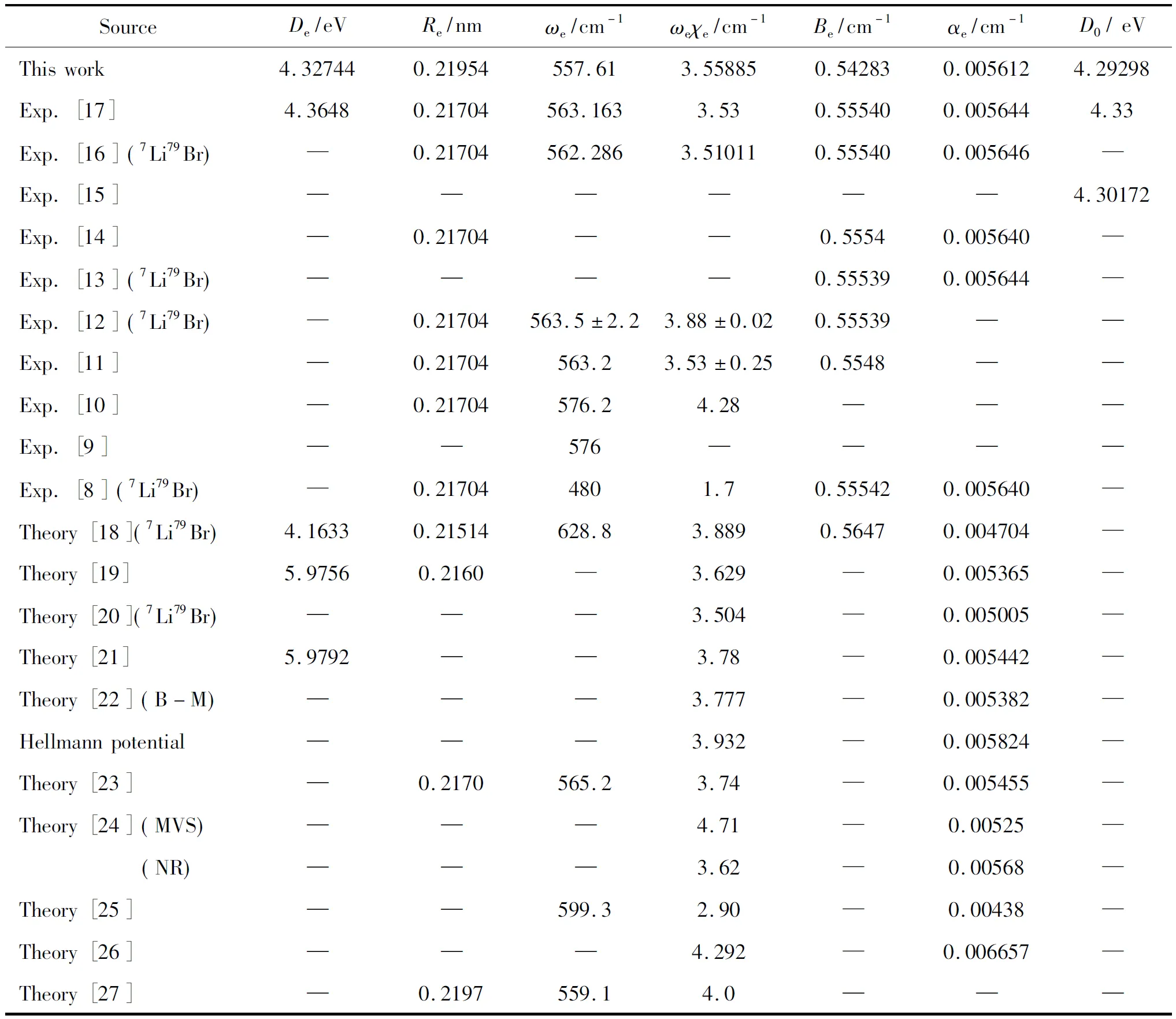
Table 1 presents the results of the MRCI calculated molecular properties (equilibrium distancesRe, harmonic frequencyωeand dissociation energyDe) and experimental data for the LiBr(X1∑+) molecule. In order to obtain more accurateRe,ωeandDe, we take into consideration the effects on these spectroscopic parameters by the relativistic corrections at these basis sets. The results obtained by the Douglas-Kroll-Hess 2ndorder (DKH2) scalar relativistic corrections and the deviations from the non-relativistic (NR) results are also listed in Table 1.

From Table 1, it is not diffcult to find that the DKH2 corrections make theResmall, thus slightly closer to the available experimental result[18]. As to theωe, the DKH2 corrections also make it better when compared with the non-relativistic calculations. Only theDebecomes further deviating from the measurement[18]under the DKH2 corrections. According to these, we think that the results obtained at the DKH2 corrections are in better accord with the experiments than those obtained at the non-relativistic calculations as a whole. Therefore, we employ the PECs obtained at the DKH2 corrections for further investigations.

Table 1 Spectroscopic parameter (Re,ωeandDe) comparisons with the latest experiments for LiBr(X1∑+) obtained by non-relativistic (NR) and DKH2 at the MRCI level of theory (Li for cc-pV5Z and Br for aug-cc-pV5Z)

3.1 APEF of the LiBr(X1∑+)

Here we use the M-S function to fit the LiBr potentials. This function can be commonly written as follows,

V(ρ)=-De(1+∑(ni=1aiρi)exp(-a1ρ).

(1)

Where,ρ=R-Re,Ris the internuclear distance of diatomic molecule.ReandDeare its equilibrium internuclear and distance dissociation energy, respectively. Which are regarded as the fixed parameters in the fitting process. The parametersai(i= 1, 2, 3,…,n) are determined by fitting.

Fitting equation (1) with the least-squares method, the parametersaiare determined. In order to attain a satisfactory result, of which the extracted spectroscopic parameters are the closest to the experiments, we try it fromn= 3 ton= 8. By comparison with the spectroscopic experiments (Be,αe,ωeχeandD0)[8, 11-14, 16, 17], we find that the best favorable results can be obtained atn= 4. The fitting results are tabulated in Table 2.

Table 2 The M-S APEF parameters for LiBr(X1∑+) by DKH2 corrections at the MRCI level of theory (Li for cc-pV5Z and Br for aug-cc-pV5Z)

In order to evaluate the fitting quality of the PEC, we calculate the root mean square error (ΔERMSE) in the fitting process,

(2)

WhereVAPEF(i) andVab initio(i) are energies attained by the fitting and by the ab initio calculations, respectively.Nis the number of fitting points (hereN= 235). The presentΔERMSEis of only 0.003279 eV (about 0.076 Kcal/mol). It shows that the M-S function is very suitable for reproducing the PEC of the LiBr(X1∑+), and the fitting process is of high quality. Therefore, the present APEF collected in Table 2 should be reliable and can be used to perform the spectroscopic and vibrational manifold calculations, such as the spectroscopic parameters, the vibrational levels, the classical turning points and the inertial rotation constants, etc.

3.2 Spectroscopic parameters (Be,αe,ωeχeandD0)

Now, we calculate the rest spectroscopic parameters (Be,αe,ωeχeandD0) of the LiBr(X1∑+) as the APEF tabulated in Table 2. Using equation (1), we can derive the expressions of the force constants, quadraticf2, cubicf3and quarticf4, at the equilibrium position as follows,

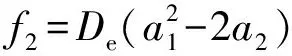
(3)

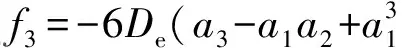
(4)

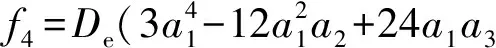
(5)

ThenthespectroscopicparametersBe, αe, ωeχeandD0canbedeterminedaccordingtothefollowingequations(6)-(9),

(6)

(7)

(8)

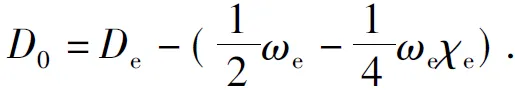
(9)

TheBe,αe,ωeχeandD0values derived at the MRCI level have been tabulated in Table 3 together with theReandωevalues for integrality. In addition, we also collect the available measurements[8-17]and other theories[18-27]in this Table for convenient comparison.

In Table 3, one can find that theDevalue at this basis set under the DKH2 corrections is good agreement with the available experiment[17], and the deviation from it[17]is of 0.86%. We also find that the presentReresult is also in accord with the experiments[8, 10-12, 14, 16, 17], and the difference between them is of 1.15%. As to theωeof the LiBr(X1∑+), different experiments[8-12, 16, 17]gave different results and the differences among these measurements[8-12, 16, 17]are very large as can be seen in Table 3. This makes it difficult for us to accurately compare the present value with them. However, on the one hand, the present basis set (Li for cc-pV5Z and Br for aug-cc-pV5Z) is a very large one; on the other hand, theDeandRevalues obtained at the MRCI level of theory are accurate. According to these, we conclude that theωevalue should be accurate. Theωedeviation between this theory and the latest experiment[16]is of only 0.83%. The rest spectroscopic parametersωeχe,Be,αeandD0reproduced from the APEF are favourite well with the measurements[10-17], too. So we can further conclude that the present APEF is credible.

Very recently, Matcha[18]calculated the spectroscopic parameters of the LiBr(X1∑+) using the self-consistent field (SCF) method. As we can see in Table 3, theDeandαevalues were too small when compared with the measurement[17], while theωevalue was too large when compared with the experiments[8-12, 16, 17]. Redingtom[19]performed theDe,Re,ωeχeandαecalculations. Unfortunately, theDevalue deviating from the measurement[17]was too large and the important constants,ωe,BeandD0, were not evaluated. Several theoretical spectroscopic investigations[20, 22, 24, 26]obtained onlyωeχeandαevalues. Obviously, other spectroscopic parameters, such asDe,Re,ωe,BeandD0, were not derived in their work. Refs. [21, 23, 25, 27] also calculated some spectroscopic parameters and their investigations were not complete.

From the above discussion, it is easy to find that the present spectroscopic investigations are more accurate and complete than those obtained by previous theories[18-27]. Therefore, we can employ the APEF tabulated in Table 2 to make the vibrational manifold calculations.

3.3 Vibrational manifolds

In order to determine the vibrational eigenvalues, we must solve the radial Schrödinger equation of nuclear motion. In the adiabatic approximation, the radial Schrödinger equation of nuclear motion can be written as,

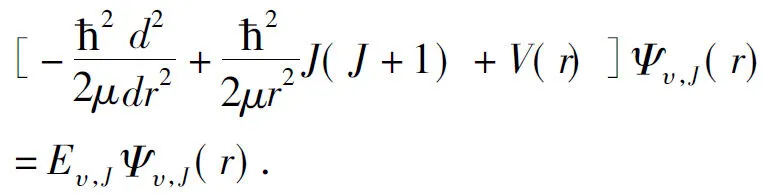
(10)

HereV(r) is the APEF tabulated in Table 2.ris the internuclear distance of two atoms, Br and Li.μis the reduced mass of the LiBr(X1∑+).υandJare the vibrational and the rotational quantum numbers, respectively.Eυ,JandΨυ,J(r) are the eigenvalues and eigenfunctions of the potentialJ(J+1)·ħ2/2μr2+V(r), respectively. The rotational sublevel of a given vibrational level is represented by the following power series,Where,G(υ) is the vibrational level.Bυis the inertial rotation constant. AndDυ,Hυ,Lυ,Mυ,NυandOυare the centrifugal distortion constants. By numerically solving equation (10) with the Numerov method[34], we have obtained a total of 126 vibrational states for the LiBr(X1∑+) when the rotational quantum numberJis set to equal zero (J=0). For each vibrational state, 1 vibrational levelG(υ), 1 inertial rotation constantBυand the classical turning points(RminandRmax) are obtained. Here, duo to the length limitation of the paper, we present only the first 20 vibrational levels, classical turning points and inertial rotation constants with the available experiments[16, 12]are all collected in Table 4.

Table 3 Spectroscopic parameter comparisons with the measurements and other theories for LiBr(X1∑+) by using DKH2 at the MRCI level of theory. In the calculations, the basis set used for Li is cc-pV5Z and for Br is aug-cc-pV5Z

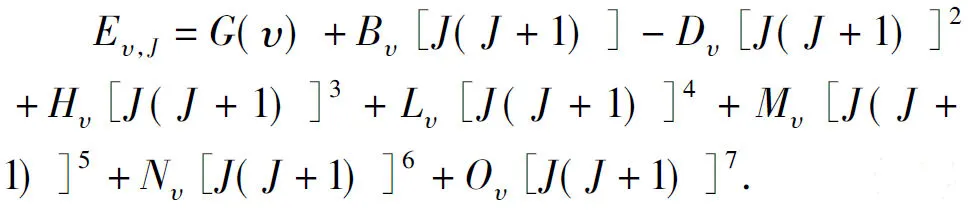
(11)

To our knowledge, in experiment, only Brazier et al.[16]determined theGυ,RminandRmaxvalues whenν≤ 9 for the LiBr(X1∑+) molecular. And Rusk and Gordy[12]obtained theBυvalues for the LiBr(X1∑+) molecular whenν=0. These results are listed in Table 4 for convenient comparisons. As a whole, the present results are in good accord with these experiments. For example, by comparison between present theory and experiment[16]in Table 4, we find that the largest deviations do not exceed 1.23%[16]forRminandRmax, 1.7%[16]forGυexcepts whenυ= 6, respectively. And by comparisonBυvalues between this theory and experiment[12]in Table 6, we also find that the deviations ofBυdo not exceed 1.4%[12]forυ=0.

By the way, we have used the present program codes to calculate the vibrational level, classical turning points and inertial rotation constants of the X1∑+,a3∑+and A1Π states of NO+ion[35].Favorable agreement exists when compared with experiments. These investigations show that the present program codes and method are reliable.

Unfortunately, to the best of our knowledge, no vibrational level and classical turning points exist anywhere whenν>9 and no inertial rotation constants can be found in the literature when the vibrational level is higher than zero for the LiBr(X1∑+) molecular. Thus, we cannot make any direct comparison among them. But according to the reliable APEF, the excellent agreement between the present spectroscopic parameters and the measurements[8-17]and the good accord of the vibrational level, classical turning points and inertial rotation constants between theory and experiments[16, 12], we conclude that the rest results collected in Table 4 must be accurate.

Table 4 Comparisons of the calculated vibrational levels, classical turning points and inertial rotation constants with experiments for LiBr(X1∑+) whenJ=0 at the MRCI level of theory

4 Conclusions

The PECs of the LiBr(X1∑+) molecular have been obtained using the MRCI theory and large correlation-consistent basis sets (cc-pV5Z for Li and aug-cc-pV5Z for Br) at the DKH2 corrections. The present spectroscopic constants, which are determined by the PECs obtained here, are in agreement with the experimental data. The first 20 vibrational levels, the classical turning points and the inertial rotation constants are also calculated whenJ=0 by numerically solving the radial Schrödinger equation of nuclear motion with the Numerov method. Comparison with the available experiments shows that the present calculations are reliable and accurate. As a whole, the present results provide more accurate and complete investigations on the molecular parameters of the LiBr(X1∑+) molecular when compared with the previous theoretical studies.

[1] Pauling L.Thenatureofthechemicalbond[M]. 3rd ed. New York: Cornell University Press, 1960.

[2] Landau L D. On the theory of transfer of energy at collisions [J].Phys.Z.Sowjetunion, 1932, 2: 46.

[3] Zener C. Non-adiabatic crossing of energy levels [J].Proc.R.Soc.Lond. A, 1932, 137 (833): 696.

[4] Binnewies M. Chemische transportreaktionen [J].Chem.UnsererZeit, 1998, 32 (1): 15.

[5] Ozaki T, Jiang J, Murase K,etal. Mutual separation characteristics for the yttrium and lanthanides with chemical vapor transport process mediated by metal chloride gaseous complexes [J].J.AlloysComp., 1998, 265 (1): 125.

[6] Hendricks J H, Aquino M I, Maslar J E,etal. Metal and ceramic thin film growth by reaction of alkali metals with metal halides: a new route for low-temperature chemical vapor deposition [J].Chem.Mater., 1998, 10 (8): 2221.

[7] Ottosson M, Andersson T, Carlsson J O,etal. Chemical vapor deposition of the superconducting YBa2Cu3O7-xphase using halides as metal sources [J].Appl.Phys.Lett., 1989, 54 (24): 2476.

[8] Honig A, Mandel M, Stitch M L,etal. Microwave spectra of the alkali halides [J].Phys.Rev., 1954, 96 (3): 629.

[9] Klemperer W, Rice S A. Infrared spectra of the alkali halides. Ⅰ. lithium halides [J].J.Chem.Phys., 1957, 26 (3): 618.

[10] Berry R S, Klemperer W. Spectra of the alkali halides. Ⅲ. Electronic spectra of lithium chloride, lithium bromide, and lithium iodide [J].J.Chem.Phys., 1957, 26 (4): 724.

[11] Klemperer W, Norris W G, B chler A,etal. Infrared spectra of lithium halide monomers [J].J.Chem.Phys., 1960, 33 (5): 1534 and references herein.

[12] Rusk J R, Gordy W. Millimeter wave molecular beam spectroscopy: alkali bromides and iodides [J].Phys.Rev., 1962, 127 (3): 817.

[13] Hebert A J, Breivogel F W, Street K. Radio-frequency and microwave spectra of LiBr by the molecular-beam eledtric-resonance method [J].J.Chem.Phys., 1964, 41 (8): 2368.

[14] Lide D R, Cahill P, Gold L P. Microwave spectrum of lithium chloride [J].J.Chem.Phys., 1964, 40 (1): 156 and references herein.

[15] Su T -M R, Riley S J. Alkali halide photofragment spectra. Ⅱ. Alkali bromide bond energies and excited state symmetries at 266 nm [J].J.Chem.Phys., 1980, 72 (3): 1614.

[16] Brazier C R, Oliphant N H, Bernath P F. Diode-laser spectroscopy of alkali halides: the lithium bromide molecule [J].J.Mol.Spectrosec., 1989, 134 (2): 421.

[17] Huber K P, Herzberg G.MolecularspectraandmolecularstructureIV.Constantsofdiatomicmolecules[M]. New York: Van Nostrand Reinhold Company, 1979.

[18] Matcha R L. Theoretical analysis of the electronic structure and molecular properties of the alkali halides. Ⅴ. potassium chloride and lithium bromide [J].J.Chem.Phys., 1970, 53 (2): 485.

[19] Redington R L. Internuclear potential energy functions for alkali halide molecules [J].J.Phys.Chem., 1970, 74 (1): 181.

[20] Brumer P, Karplus M. Perturbation theory and ionic models for alkali halide systems. diatomics [J].J.Chem.Phys., 1973, 58 (9): 3903.

[21] Finn E J. Spectroscopic constants of the Rittner potential evaluated by the Dunham method [J].J.Chem.Phys., 1975, 62 (5): 1842.

[22] Shanker J, Agrwal H B, Agrawal G G. Theory of interionic forces in alkali halide molecules [J].J.Chem.Phys., 1980, 73(8): 4056.

[23] Kumar M, Kaur A J, Shanker J. Spectroscopic constants of alkali halides and hydrides using modified T-Rittner model [J].J.Chem.Phys., 1986, 84 (10): 5735.[JP]

[24] Kumar M, Shanker J. Electronic polarizabilities, potential functions, and spectroscopic constants for diatomic molecules of alkali halides and alkali hydrides [J].J.Chem.Phys., 1992, 96 (7): 5289.

[25] Dotelli G, Lombardi E, Jansen L. Model analysis of bonding in the alkali halide molecules [J].J.Mol.Struct. (Theochem), 1994, 306 (2-3): 177.

[26] Hati S, Datta B, Datta D. Polarizability of an ion in a molecule. Applications of Ritter’s model to alkali halides [J].J.Phys.Chem., 1996, 100 (51): 19808.

[27] Bacskay G B, Buckingham A D. Nuclear quadrupole coupling constants in alkali halide molecules: an ab initio quantum chemical study [J].Mol.Phys., 1997, 91 (3): 391.

[28] Knowles P J, Werner H J. An efficient second-order MC SCF method for long configuration expansions [J].Chem.Phys.Lett., 1985, 115 (3): 259.

[29] Werner H J, Knowles P J. An efficient internally contracted multiconfiguration-reference configuration interaction method [J].J.Chem.Phys., 1988, 89 (9): 5803.

[30] Knowles P J, Werner H J. An efficient method for the evaluation of coupling coefficients in configuration interaction calculations [J].Chem.Phys.Lett., 1988, 145 (6): 514.

[31] Fermann J T, Sherrill C D.SomeCommentsonMulti-ReferenceCI(MRCI) [M]. 1996.

[32] Werner H J, Knowles P J, Lindh R,etal. 2008 MOLPRO, version 2008.1, a package of ab initio programs.

[33] (a) Dunning Jr T H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen [J].J.Chem.Phys., 1989, 90 (2): 1007. (b) Kendall R A, Dunning Jr T H, Harrison R J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions [J].J.Chem.Phys., 1992, 96 (9): 6796. (c) Woon D E, Dunning Jr T H. Gaussian basis sets for use in correlated molecular calculations.Ⅰ. Core-valence basis sets for boron through neon [J].J.Chem.Phys., 1995, 103 (11): 4572.

[35] Zhang J P, Cheng X L, Zhang H,etal. Spectroscopic investigations on NO+(X1∑+, a3∑+, A1П) ion using MRCI method and correlation-consistent sextuple basis set augmented with diffuse functions [J].Chin.Phys. B, 2011, 20 (6): 060401.

Theoretical investigation on spectroscopic parameters and
molecular constants of LiBr(X1∑+) molecule

ZHANG Jin-Ping, TIAN Kai, LI Hui, ZHANG Yang-Yang

(College of Information Engineering, Huanghe Science and Technology College, Zhengzhou 450006, China)

Abinitiocalculations using multireference configuration interaction (MRCI) theory in combination with a series of correlation-consistent basis sets are used to determine the accurate spectroscopic parameters (Re,ωeandDe) and potential energy curves for the ground state of diatomic molecules LiBr. We discuss the Douglas-Kroll-Hess 2ndorder scalar relativistic effects on bond lengths, harmonic frequencies and dissociation energies of LiBr. The potential energy curves are all fitted to the Murrell-Sorbie function, which are used to accurately reproduce the spectroscopic parameters such asωeχe,αe,BeandD0, which are in excellent agreement with experimental values. Based on the analytical potential energy function, the total vibrational manifolds of LiBr are calculated by numerically solving the radical Schrödinger equation of nuclear motion. For each vibrational state, the vibrational level, classical turning points and inertial rotation constants are obtained, which are in agreement with the available experiments.

Spectroscopic parameter; Potential energy curve; Molecular constant; Relativistic correction

2014-06-04

河南省科技厅科技发展计划项目(142300410282, 142102210136)；河南省教育厅科学技术重点项目(13B140986, 13B430985)；郑州市科技局科技攻关项目(20130679, 121PYFZX178)

张金平(1983—)，女，河南省郑州市人，博士，讲师，主要研究领域为原子、分子结构与光谱,含能材料结构与性质.E-mail: jinping213@163.com

103969/j.issn.1000-0364.2015.08.007

O561.1

A

1000-0364(2015)08-0564-08