冷却速率对Lennard-Jones体系凝固过程中结构与动力学性质的影响

杨邦鍫，孙永丽，孙亚娟，杨 平，厉华明

(1. 太原理工大学物理与光电工程学院，太原 030024； 2. 天津工业大学理学院，天津 300160)

冷却速率对Lennard-Jones体系凝固过程中结构与动力学性质的影响

杨邦鍫1，孙永丽1，孙亚娟2，杨 平1，厉华明1

(1. 太原理工大学物理与光电工程学院，太原 030024； 2. 天津工业大学理学院，天津 300160)

用分子动力学模拟方法研究了五种不同冷却速率对Lennard-Jones体系凝固过程中结构与动力学性质的影响.采用两种不同的方法来确定玻璃转变温度Tg，并且对结晶温度Tc、径向分布函数g(r)、均方位移函数MSD与扩散系数D、平均配位数进行比较分析.结果表明：冷却速率影响Lennard-Jones体系凝固过程中的结构.当使用足够高的冷却速率冷却时，体系发生玻璃化转变，而且冷却速率越快，玻璃转变温度越高；当冷却速率较小时，体系形成晶体，而且冷却速率越慢，结晶温度越高，结晶程度也越高.同时发现，冷却速率对扩散系数和平均配位数也有很大影响，二者在体系发生玻璃转变时都有一个缓变的过程，表明了过冷液相区的存在.

Lennard-Jones体系； 冷却速率； 结构； 动力学性质

1 引 言

分子动力学模拟自产生以来得到广泛的应用，特别随着计算机技术的高速发展，更是得到了绝大多数研究者的青睐.分子动力学模拟可以研究各种类型的材料，比如高分子材料[1-3]、金属材料[4-6]、非晶体合金[7-9]等.近年来关于液态金属凝固过程中微观结构的演变特性引起了研究者的广泛关注和重视，而冷却速率对其微观结构的影响也引起了激烈的讨论[10,11].其中液态金属Cu的快速凝固的模拟研究取得了许多重大的进展，这些研究所采用的模型势有FS势[12]、TB势[13]、EAM势[14,15]、由Wang等人[16]所发展的扩展非局域模型赝势[17]、Quantum Sutton-Chen (QSC)[18,19]多体势[20]等.由此可见，即使研究同一种金属材料，也能采用不同的势函数进行分析.

为此，本文采用Lennard-Jones模型，对液态Lennard-Jones体系在五个不同冷却速率下的凝固过程进行模拟研究，分析其结晶温度Tc与玻璃转变温度Tg、径向分布函数g(r)、均方位移函数MSD与扩散系数D、平均配位数，以较为深入的研究冷却速率对Lennard-Jones体系凝固过程中结构与动力学性质的影响.

2 模拟条件与方法

模拟计算的条件为：将4000个Lennard-Jones原子置于一立方体盒中, 然后让体系在周期性边界条件下运行.Lennard-Jones原子间的相互作用势为

(1)

式中，r表示原子间的距离.本文采用对比单位(Reduced unit s) , 用*表示，并以原子半径σ、原子间相互作用能量和原子质量m作为基本单位.

模拟计算均从T*=1.0开始，首先让体系等温等压运行50000 步使之处于平衡态，再分别以9.672×1011K/s，4.836×1011K/s，1.209×1011K/s，3.023×1010K/s，1.209×1010K/s的冷却速率冷却至T*=0.1，其中温度每隔0.05让体系进行一次充分弛豫，以测量该体系的结构组态, 即记录下每个原子的空间坐标.根据这些记录，对五个不同冷却速率下各温度的径向分布函数进行对比分析，并且分析其它相关量，以探讨不同冷却速率对Lennard-Jones体系快速凝固过程中结构与动力学性质的影响.

3 模拟计算结果与分析

3.1 结晶温度Tc与玻璃转变温度Tg分析

在不同冷却速率下，液体在凝固后可以得到晶体与非晶体，生成晶体的温度被定义为结晶温度Tc，生成非晶的温度被定义为玻璃转变温度Tg.图1 给出了Lennard-Jones体系在不同冷却速率下平均原子体积随温度的变化关系.可以看出，在冷却速率为9.672×1011K/s，4.836×1011K/s与1.209×1011K/s时，在降温过程中平均原子体积没有急剧的减少，说明在这三种冷却速率下，Lennard-Jones体系形成了非晶结构.反之，在3.023×1010K/s与1.209×1010K/s的冷却速率下，平均原子体积出现明显的转折，说明体系已经形成晶体.此外，从图中还可以看出，在形成晶体的两种冷却速率下，平均原子体积出现的转折点不一致，且速率较小的转折点所对应的温度较高，说明冷却速率越慢，结晶温度Tc越高.

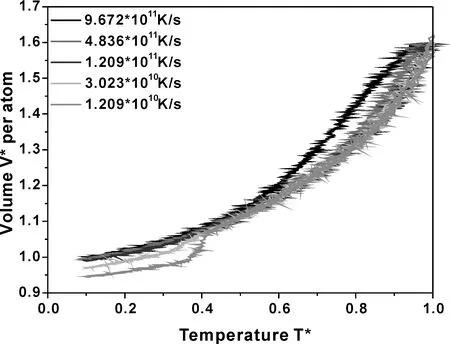
图1 Lennard-Jones体系在不同冷却速率下平均原子体积随温度的变化关系Fig. 1 The average atomic volume as a function of temperature for Lennard-Jones system at different cooling rates

玻璃转变温度Tg是判定非晶形成能力的重要参数(Trg=Tg/Tl)[21]，因此对于玻璃转变温度的测量是一个关键问题.下面采用两种常用的方法来确定玻璃转变温度Tg.

(1)体积变化判定法

这种方法是根据液体在快速冷却过程中，发生玻璃化转变时体积与温度的变化关系，将曲线两端的直线部分外推至相交[22,23]，交点即为Tg，如图2(a)所示(红色箭头所指即为玻璃转变温度Tg).由此可见，采用这种方法来计算玻璃转变温度所需要的数据比较容易得到，而且在实验测定和计算模拟都可以应用.

(2)径向分布函数参量法

这种方法是 Wendt-Abraham等人[24]提出的一种根据非晶化转变前后的结构变化来确定玻璃转变温度Tg的方法.这种方法首先定义一个参量R=gmin/gmax(g(r)曲线第一波谷的谷值与第一波峰的峰值之比)，然后通过不同温度下的R值与温度的关系，得到斜率不同的两条直线，其中的斜率变化点，即是玻璃转变温度Tg，如图2(b)所示(黑色箭头所指即为玻璃转变温度Tg).

通过比较分析图2(a)和图2(b)，可以发现这两种方法所确定的玻璃转变温度Tg相差不大.同样的，我们可以利用这两种方法分别对冷却速率为4.836×1011K/s与1.209×1011K/s的情况进行分析，确定各自的玻璃转变温度Tg.结果表明，当使用足够高的冷却速率进行冷却时，Lennard-Jones体系在快速凝固后形成非晶，而且冷却速率越快，玻璃转变温度Tg越高.

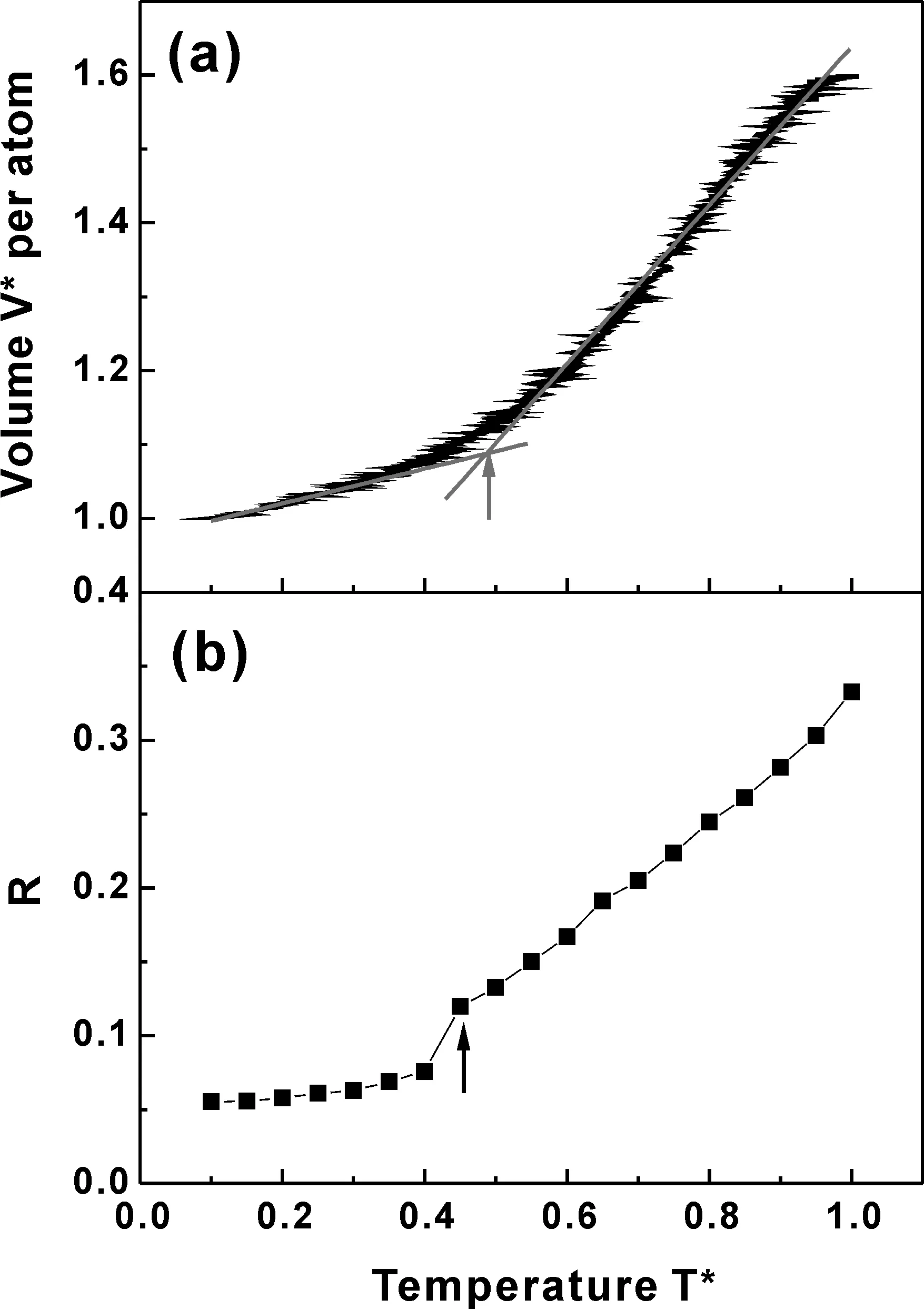
图2 冷却速率为9.672×1011 K/s时Lennard-Jones体系的平均原子体积和径向分布函数参量R随温度的变化关系Fig. 2 The average atomic volume and the radial distribution function parameter R as a function of temperature for Lennard-Jones system at the cooling rate of 9.672×1011 K/s

3.2 径向分布函数g(r)分析

径向分布函数g(r)被广泛用来描述液态和非晶态的结构特征，它表示距离原子r位置处发现另一原子的几率.图3(a)、(b)分别给出了液态下Lennard-Jones体系在冷却速率为9.672×1011K/s，1.209×1010K/s时的径向分布函数g(r*)曲线随温度的变化情况.从图中可以看出，随着温度的降低，第一个波峰由驼峰逐渐变高变锐.根据径向分数函数的定义，这种情况说明了距离原子r位置处发现另一原子的几率越来越大，表明了体系内相邻原子成键的几率也越来越大，有序度逐渐加强.在冷却速率为9.672×1011K/s的快速冷却下，当温度降到T*=0.4时，g(r*) 曲线的第二峰开始出现劈裂, 而且随着温度的降低，第二峰劈裂的越来越明显，并且劈裂的两个峰是前高后低.这正是非晶态金属结构的重要特征之一，这也表明快速冷却到T*=0.4附近就开始形成非晶.

从图3(b)可见，g(r*)曲线从T*=0.4开始，在第二峰与第三峰前后，明显出现了多个无规律的小峰，与冷却速率为3.023×1010K/s时的相比，这个速率下各小峰出现的位置和形状更有规律.说明体系在冷却速率为1.209×1010K/s时的结晶有序度比冷却速率为3.023×1010K/s时的要高.

图3 各冷却速率下径向分布函数g(r*)曲线随温度的变化关系 (a) 9.672×1011 K/s；(b) 1.209×1010K/sFig. 3 The radial distribution function g(r*) as a function of temperature at different cooling rates (a) 9.672×1011 K/s；(b) 1.209×1010 K/s

为了比较分析不同冷却速率下体系形成的固体结构，图4分别给出了不同冷却速率下各个温度的径向分布函数的对比关系.由于文中采用了五种冷却速率，有三种速率使系统玻璃化，另外两种晶化，所以根据这种这种情况将冷却速率分为两组，如图4(a)、(b)所示.由图可见，在T*=0.5时径向分布函数g(r*)在不同冷却速率下几乎完全一致，说明在液态时的g(r*)与冷却速率无关.比较图4(a)和图4(b)，可以发现图4(b)中的g(r*)相对于图4(a)的较敏感，而且图4(a)的三种冷却速率下g(r*)曲线在体系玻璃化后几乎完全重合，说明使系统玻璃化的不同冷却速率对体系玻璃化所形成的径向分布函数无多大影响.但对于使系统结晶的不同冷却速率来说，由图4(b)可见，温度从T*=0.4开始，两种冷却速率下的g(r*)均有明显的第一峰和第二峰.而且随着冷却速率的降低，第一峰和第二峰在强度上都有所升高，但第一峰的宽度有所减小，致使第一近邻配位数减少,有序度增强.在第一峰和第二峰之间均出现了肩峰，说明在液态体系在冷却过程中形成了一种中程有序结构(MRO)[25].

3.3 均方位移函数MSD与扩散系数D分析

均方位移(Mean square displacement，简称MSD)描述了体系中原子在t时间内的平均位移的平方.其表达式为

MSD=〈|ri(t+t0)-ri(t0)|2〉

(2)

式中，ri(t0)表示原子在t0时刻的位置，〈...〉表示系综平均.根据Einstein关系[26]，它与扩散系数满足如下关系式

(3)

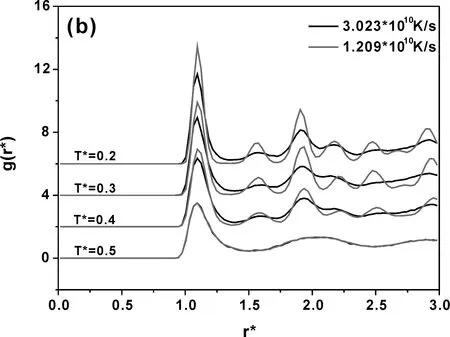
图4 不同冷却速率下各个温度的径向分布函数的对比关系Fig. 4 Comparison of the radial distribution function of each temperature at different cooling rates

其中，c是常数，D是扩散系数.由此可知扩散系数D可以通过均方位移随时间的变化曲线的斜率计算得到.

图5给出了在冷却速率为4.836×1011K/s与3.023×1010K/s时扩散系数D随温度的变化关系.由图可见，温度从T*=1下降到T*=0.45，两种冷却速率下lnD随1/T*的变化曲线完全重合，而且呈线性关系，说明原子扩散系数D随温度T*的变化满足Arrhenius关系，即lnD～1/T*.对于冷却速率为4.836×1011K/s的曲线来说，温度下降至T*=0.45之后，D随T*的变化偏离Arrhenius关系，且有一个缓变的过程，说明体系进入了过冷液相区.待温度下降至T*=0.4后，两种冷却速率下的扩散系数D基本不随温度的变化，说明此时体系流动性很小，已经凝固成晶体或非晶体.

图5 在冷却速率为4.836×1011 K/s与3.023×1010 K/s时扩散系数D随温度的变化关系Fig. 5 The diffusion coefficient D as a function of temperature at cooling rates of 4.836×1011 K/s and 3.023×1010 K/s

3.4 平均配位数的分析

配位数是指体系中任一原子周围最近邻且距离近于相等的原子数目[27]，是表征物质结构的基本参数.我们在模拟研究中发现，体系在冷却过程中，其原子的平均配位数(第一近邻)随温度的变化较为敏感.由此我们给出了两种冷却速率下(冷却速率分别为9.672×1011K/s与1.209×1010K/s)平均配位数随温度的变化关系，如图6所示.

由图可以明显看出，在两种冷却速率下，体系的原子平均配位数随温度的变化在高温时差别很小，而且都随着温度的降低而增大，而当温度降到T*=0.4以下时则有明显的不同.以较快的冷却速率(9.672×1011K/s)冷却时，体系在凝固形成非晶的过程中，其平均配位数先是比较稳定而缓慢地增加，其后保持不变，说明了非晶态的形成；而以较慢的冷却速率(1.209×1010K/s)冷却时，体系的原子平均配位数在T*=0.4以下基本保持不变，说明晶体已经形成.由此可见，平均配位数可以在某种程度上反映出Lennard-Jones体系在凝固过程中微观结构的演变特性，因而它可以作为一种方法来研究体系的结晶与玻璃化转变.

4 结 论

根据上述五种不同冷却速率对液态Lennard-Jones体系凝固过程中结构与动力学性质的影响的模拟研究结果和讨论，可得如下结论：

(1)冷却速率对结晶温度与玻璃转变温度的影响.当冷却速率为3.023×1010K/s与1.209×1010K/s时，体系形成晶体，而且冷却速率越慢，结晶温度Tc越高；当冷却速率为9.672×1011K/s，4.836×1011K/s与1.209×1011K/s时，体系发生玻璃化，而且冷却速率越快，玻璃转变温度Tg越高.

(2)冷却速率对Lennard-Jones体系形成的最终固体结构的影响.当使用足够高的冷却速率进行冷却时，冷却速率对Lennard-Jones体系发生玻璃化后所形成的径向分布函数无多大影响；反之，当使用的冷却速率过慢致使Lennard-Jones体系结晶时，冷却速率对Lennard-Jones体系发生晶化后所形成的径向分布函数有很大影响，而且冷却速率越慢，有序度越强，结晶程度也越高.

(3)冷却速率对扩散系数的影响.当Lennard-Jones体系在高温液体时，原子扩散系数D随温度T*的变化满足Arrhenius关系，即lnD～1/T*，与冷却速率无关；而当冷却速率足够高致使Lennard-Jones体系形成非晶时，原子扩散系数D不会随温度T*发生突变，而是有一个缓变的过程，说明了过冷液相区的存在.

(4)冷却速率对平均配位数的影响.不同冷却速率下Lennard-Jones体系的原子平均配位数在刚开始降温阶段都会随温度的降低而增大.而在高温液体之后，若使用的冷却速率过快致使Lennard-Jones体系形成非晶，那么其平均配位数先是比较稳定而缓慢地增加，而后保持不变；若使用的冷却速率过慢致使Lennard-Jones体系结晶，那么在其结晶后平均配位数一直保持不变，没有一个缓变的过程.

[1] Yao D G, Kim B Y. Simulation of the filling process in micro channels for polymeric materials [J].J.Micromech.Microeng., 2002, 12(5): 604.

[2] Qiao R, Brinson L C. Simulation of interphase percolation and gradients in polymer nanocomposites [J].Compos.Sci.Technol., 2009, 69(3): 491.

[3] Liu Z S, Hong W, Suo Z G,etal. Modeling and simulation of buckling of polymeric membrane thin film gel [J].Comp.Mater.Sci., 2010, 49(1): S60.

[4] Yoshidaa F. Material models for accurate simulation of sheet metal forming and springback [J].AIPConf.Proc., 2010, 1252: 71.

[5] Taherizadeh A, Green D E, Ghaei A,etal. A non-associated constitutive model with mixed iso-kinematic hardening for finite element simulation of sheet metal forming [J].Int.J.Plasticity, 2010, 26(2): 288.

[6] Toni M D, Coudert F X, Paranthaman S,etal. Molecular simulation of a Zn-triazamacrocyle metal-organic frameworks family with extraframework anions [J].J.Phys.Chem. C, 2012, 116(4): 2952.

[7] Schenk T, Holland M D, Simonet V,etal. Icosahedral short-range order in deeply undercooled metallic melts [J].Phys.Rev.Lett., 2002, 89(7): 075507.

[8] Luo W K, Sheng H W, Alamgir F M,etal. Icosahedral short-range order in amorphous alloys [J].Phys.Rev.Lett., 2004, 92(14): 145502.

[9] Huang L, Wang C Z, Hao S G,etal. Short- and medium-range order in amorphous Zr2Ni metallic alloy [J].Phys.Rev. B, 2010, 81(9): 094118.

[10] Yi X H, Liu R S, Tian Z A,etal. Formation and evolution properties of clusters in liquid metal copper during rapid cooling processes [J].Trans.NonferrousMet.Soc.China, 2008, 18(1): 33.

[11] Wang J F, Huang S, Guo S F,etal. Effects of cooling rate on microstructure, mechanical and corrosion properties of Mg-Zn-Ca alloy [J].Trans.NonferrousMet.Soc.China, 2013, 23(7): 1930.

[12] Zhang T, Zhang X R, Ding S L. The molecular dynamics simulation of cooled liquid Cu by FS potential model [J].J.At.Mol.Phys., 2003, 20 (3): 357 (in Chinese) [张弢, 张晓茹, 丁世良. 用FS多体势模型模拟金属铜的冷却过程[J]. 原子与分子物理学报, 2003, 20(3): 357]

[13] Liu C S, Xia J C, Zhu Z G,etal. The cooling rate dependence of crystallization for liquid copper: A molecular dynamics study [J].J.Chem.Phys., 2001, 114(17): 7506.

[14] Chen F F, Zhang H F, Qin F X,etal. Molecular dynamics study of atomic transport properties in rapidly cooling liquid copper [J].J.Chem.Phys., 2004, 120(4): 1826.

[15] Pang H, Jin Z H, Lu K. Relaxation, nucleation, and glass transition in supercooled liquid Cu [J].Phys.Rev. B, 2003, 67(9): 094113.

[16] Wang S, Lai S K. Structure and electrical resistivities of liquid binary alloys [J].J.Phys. F:Met.Phys. , 1980, 10(12): 2717.

[17] Lin Y, Liu R S, Tian Z A,etal. Effect of cooling rates on microstructures during solidification process of liquid metal Zn [J].ActaPhys.Chim.Sin. , 2008, 24(2): 250 (in Chinese)

[18] Qi Y, Cagin T, Kimura Y,etal. Molecular-dynamics simulations of glass formation and crystallization in binary liquid metals: Cu-Ag and Cu-Ni [J].Phys.Rev. B, 1999, 59(5): 3527.

[19] Sutton A P, Chen J. Long-range finnis-sinclair potentials [J].Philos.Mag.Lett., 1990, 61(3): 139.

[20] Yi X H, Liu R S, Tian Z A,etal. Simulation study of effect of cooling rate on evolution of microstructures during solidification of liquid metal Cu [J].ActaPhys.Sin., 2006, 55(10): 5386 (in Chinese)

[21] Turnbull D. Under what conditions can a glass be formed? [J].Contemp.Phys., 1969, 10(5): 473.

[22] Berthier L, Biroli G. Theoretical perspective on the glass transition and amorphous materials [J].Rev.Mod.Phys., 2011, 83(2): 587.

[23] Biroli G, Garrahan J P. Perspective: The glass transition [J].J.Chem.Phys., 2013, 138(12): 12A301.

[24] Abraham F F. An isothermal-isobaric computer simulation of the supercooled liquid/glass transition region: Is the short-range order in the amorphous solid fcc? [J].J.Chem.Phys., 1980, 72(1): 359.

[25] Li H. Shoulder-peak formation in the process of quenching [J].Phys.Rev. B, 2003, 68(2): 024210.

[26] Barkai E, Fleurov V N. Generalized Einstein relation: A stochastic modeling approach [J].Phys.Rev. E, 1998, 58(2): 1296.

[27] Zhou L L, Liu R S, Hou Z Y,etal. Simulation study of effects of cooling rate on evolution of micro-cluster structures during solidification of liquid Pb [J].ActaPhys.Sin., 2008, 57(6): 3653 (in Chinese)

Effects of cooling rates on structures and kinetic properties during solidification process of the Lennard-Jones system

YANG Bang-Qiao1, SUN Yong-Li1, SUN Ya-Juan2, YANG Ping1, LI Hua-Ming1

(1.College of Physics and Optoelectronics, Taiyuan University of Technology, Taiyuan 030024, China;2. School of Science, Tianjin Polytechnic University, Tianjin 300160, China)

A molecular dynamics simulation study was performed for the effects of five different rates on structures and kinetic properties during solidification process of the Lennard-Jones system. Glass transition temperatureTgwas measured by using two different methods, and the crystallization temperatureTc, the radial distribution function, the mean square displacementMSD, the diffusion coefficientDand the mean coordination number were used to compare and analyze. The results show that the cooling rate plays a critical role on structures during solidification process of the Lennard-Jones system. As the cooling rate being high enough, the system will be transferred into glass, and the greater the cooling rate, the higher the glass transition temperature. As the cooling rate being smaller, the system will be crystallized, and the slower the cooling rate, the higher the crystallization temperature, and the higher the degree of crystallization. At the same time, it is found that the diffusion coefficient and the mean coordination number are largely influenced by cooling rates, and both have a slow graded process of the glass transition occurred in the system, which shows the existence of supercooled liquid region.

Lennard-Jones system; Cooling rate; Structure; Kinetic property

国家自然科学基金项目(11204200)

杨邦鍫(1989—),男，浙江温州人，硕士研究生，研究方向为分子动力学模拟.E-mail: daxuewuli001@163.com

孙永丽. E-mail: sunyongli@tyut.edu.cn

103969/j.issn.1000-0364.2015.08.022

O751

A

1000-0364(2015)08-0647-06

投稿日期:2013-12-08