α-BeH2电子结构与光学性质的第一性原理研究

彭 敏，韦建军，张 季，刘 丽,

( 1. 新疆工程学院基础部，乌鲁木齐 830091； 2. 四川大学原子与分子物理研究所，成都 610065)

α-BeH2电子结构与光学性质的第一性原理研究

彭 敏1，韦建军2，张 季1，刘 丽1, 2

( 1. 新疆工程学院基础部，乌鲁木齐 830091； 2. 四川大学原子与分子物理研究所，成都 610065)

基于密度泛函理论，采用赝势平面波方法研究了α-BeH2的结构、电子和光学性质.基态下，α-BeH2晶格常数a和体积弹性模量B0计算值与实验值及其它理论值一致.根据能带理论研究了α-BeH2基态下的能带结构、总态密度(DOS)和分波态密度(PDOS).经过分析发现α-BeH2为直接能隙半导体材料，能隙为5.44 eV，与文献相比，本文计算的结果偏低，这主要是利用第一性原理中的局域密度近似(LAD)或广义梯度近似(GGA)交换关联能函数计算材料的带隙宽度或者磁耦合的理论结果均会偏低.通过对基态α-BeH2的Mulliken电荷分布和集居数的分析发现：α-BeH2属于离子键和共价键所形成的混合键化合物；α-BeH2的电荷总数分别来源于H 1s轨道，Be 2s和2p轨道.同时本文还分析研究了α-BeH2的光学介电函数、吸收系数、复折射率、反射系数和能量损失等光学性质.

第一性原理; α-BeH2; 光学性质; 介电函数

1 引 言

由于BeH2在科学和技术上有着潜在的应用价值，因而引起了人们的广泛兴趣.BeH2有一系列独特的核物理性质：低原子质量；固体BeH2(或BeD2,BeDT)中氢同位素浓度高；对热中子的捕获截面低，热中子散射截面高，可以作为反应堆中子减速物质.BeH2粉末含能高，用作火箭固体推进燃料，可以提供碳氢推进燃料两倍的动力[1].BeH2是压稳态氢化物，稍微加热就会分解释放出氢气，故可以作为储氢材料[2].此外，BeH2可以作为烧蚀层材料应用在惯性约束聚变(ICF)中[3]，由于含铍烧蚀层材料元素核电荷少和低压缩，具有相对高的密度.其优良的性能组合在高效激光辐射吸收和等离子体自身辐射的低能量损耗下，确保了压缩热核物质活塞具有良好的流体动力学特性.在具有高热核增益因子(100或更高，对应激光能量5～10 MJ)的反应堆靶燃烧时，靶中心区传出的热冲击波可以达到明显高于DT或DD反应的温度阈值，含热核燃料的壳层—烧蚀层燃烧显著地增加了能量效益[4].自从1933年发现BeH2以来，已经有各种各样的制备方法报道.1951年，Schlesinger等[5]通过含醚二叔丁基铍和LiAlH4反应合成了质量纯度为50%的BeH2；1954年，Coates等[6]通过含醚二叔丁基铍在150-210度热分解制备出了质量纯度为70%的BeH2.1957年，Holley等[7]改进了Coates的方法，利用二叔丁基铍在氮气的保护下制备出白色多孔的BeH2粉末.1999年, Yu.E.Markhushkin等[8]用化学气相沉积技术，在低压氘氚气氛下，蒸发的金属铍和非平衡氘原子反应，生成的BeD2沉积到半球壳基底上.结果显示：在球表面的极点处，氘化铍薄膜的厚度最小，接近边缘处，厚度增加.但由于BeH2具有毒性和制备高纯度BeH2困难，对该材料的研究较少，尤其是在国内，对该材料的研究几乎是空白.理论上，2004年P.Vajeeston等人[9]采用第一性原理并根据能量最低原理进行了详细地研究.结果表明：α-BeH2在7.07 GPa时转变为β-BeH2; β-BeH2在51.41 GPa时转变为γ-BeH2; γ-BeH2在86.56 GPa时转变为δ-BeH2; 最后δ-BeH2在97.55 GPa时转变为ε-BeH2.但从理论上对BeH2的介电函数、折射系数、能量损失谱等光学性质的研究报道相对较少，为此本文基于密度泛函理论详细研究了α-BeH2的光学性质，对BeH2材料的实验研究具有重要的指导意义.

2 计算方法

高压情况下BeH2主要有五种结构[9]：α-BeH2、β-BeH2、γ-BeH2、δ-BeH2和ε-BeH2.本文根据密度泛函理论和赝势平面波方法，通过MS5.5中的CASTEP模块[11]计算α-BeH2的结构、电子性质和光学性质.晶体波函数由平面波基矢展开，交换关联函数选取广义梯度近似GGA中Perdew Burke Ernzerh (PBE)泛函形式[12],赝势采用平面波超软赝势[13].体系中赝势原子Be:2s2，H:1s1视为价电子处理.平面波的截止能量Ecut=450 eV，沿对称布里渊区(BZ)方向Monkhorst-Pack K点[14]取6×8×6,对结构优化采用了BFGS[15]方法，自洽计算体系总能收敛小于2×10-5eV/atom, 原子受力低于0.05 eV/Å，公差偏移小于1×10-5Å，应力偏差小于0.01 GPa.

3 结果和讨论

3.1 α-BeH2结构

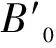
图1 α-BeH2结构Fig. 1 The structure of α-BeH2

表1 α-BeH2的晶格常数a、体弹模量B0和能隙Eg

Table 1 The lattice constanta, bulk modulusB0and band gapEgof α-BeH2

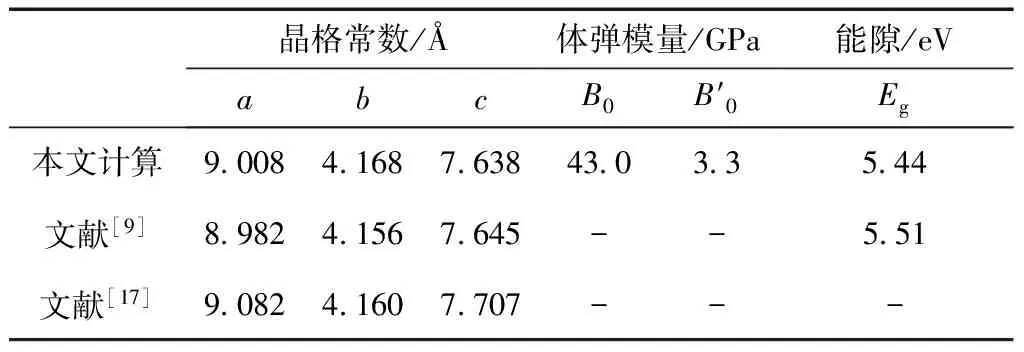
晶格常数/Åabc体弹模量/GPaB0B′0能隙/eVEg本文计算9 0084 1687 63843 03 35 44文献[9]8 9824 1567 645--5 51文献[17]9 0824 1607 707---

3.2 α-BeH2的电子性质、Mulliken电荷布居和重叠布居数分析

在几何优化的基础之上计算了α-BeH2的能带结构、总态密度(DOS)和分波态密度(PDOS).图2为α-BeH2沿布里渊区高对称方向积分计算得到的能带结构和态密度图.零点能选在费米能级处.经过分析，α-BeH2的直接禁带宽度 (价带顶G点到导带底G点)Eg为5.44 eV，文献[9]为5.51 eV.本文计算的结果偏低，主要原因是利用第一性原理中的局域密度近似(LAD)或广义梯度近似(GGA)交换关联能函数计算材料的带隙宽度或者磁耦合的理论结果均会偏低[18]，为了使结果更接近实验值或其他理论值，可以采用剪刀算符[19]对能量进行修正.从能带结构可以看α-BeH2属于直接带隙半导体材料.结合图2中右侧给出的α-BeH2总态密度(DOS)和分波态密度(PDOS)可知:下价带-6.61到-2.20 eV之间的峰主要来源于H 1s态电子和Be 2p态电子以及少量的Be 2s态电子和Be 2p态电子杂化贡献.费米能级附近的上价带区间(即: -2.20到0 eV)的峰主要由H 1s态电子，Be 2p态电子贡献.从整体来看，整个价带区间的电子态都是非局域态.能带区间5.44到8.72 eV之间的峰是H 1s态电子，Be 2s和2p态电子共同贡献，整个导带区间的电子态也是非局域态.关于α-BeH2能带其它重要信息，特别是禁带宽度，详见表2所示.

在计算分析了α-BeH2的能带结构和态密度之后还计算了其Mulliken电荷分布[20,21].表3和表4所列为α-BeH2的Mulliken电荷布居分析和重叠布居数.表3为α-BeH2的Mulliken电荷布居分析, 电荷为正表示失去电子，电荷为负表示得到电子.在α-BeH2结构中，H 1s轨道和Be 2p轨道占有的电子对α-BeH2电荷总数有主体贡献.H净原子区域集居数分别为-0.30和-0.32，Be净原子区域布居数分别为：0.63和0.61，说明电荷主要从Be原子向H原子转移.H1和H2 1s轨道占据的电子数分别为1.30和1.32；Be1和Be2 2p轨道占据的电子数分别为1.13和1.14.占据Be1和Be2 2s态的电子数目明显少于2p态的电子数目.或者可以这样说，较其自由状态，在其形成化合物过程中，占据Be1和Be2 2s态的电子向2p态转移.α-BeH2沿(002)方向的差分态密度如图3所示.材料的共价特性主要是取决于体系中阴阳离子间共用电子对的形成，而离子特性则主要取决于体系中阴阳离子间电荷的转移.从图中可知，电荷主要集居在H原子周围，且从表4中可知，沿Be-H键方向形成了一较强的共价键，主要起源于H 1s和 Be 2p轨道的sp3杂化.表4为α-BeH2的Mulliken重叠布居数[20,22]，其中正、负布居数分别表示两原子间的成键与反成键.布居数为零或接近于零表明原子之间没有或无明显成键.从表4中我们H-H键原子之间有负的重叠布居数，这说明α-BeH2结构中存在反键态；H-Be键原子之间除了个别的重叠布居数显示为负外，其余都为较大的正数，说明α-BeH2结构中存在成键态，性质表现为极为强的共价性；Be-Be键原子之间有正的重叠布居数，说明该原子之间也存在共价性较强的成键态.同时还发现，同种原子键之间，重叠布居数越大，其键长就越短，拥有较强的结合能.通过以上分析可知，α-BeH2是一个共价性较强而离子性较弱的混合金属氢化物材料.H-Be离子键形成的原因可以这样分析：占据Be 2s轨道高能态的价电子跃迁到低能态的H 1s的空轨道上；H-Be共价键的形成则是H 1s与Be 2p轨道在能级为2.20 eV和费米能级附近(根据基态下的能带和PDOS分波态密度判定)杂化形成的杂化轨道，杂化轨道与H 1s轨道线性组合成反键态和成键态高低能级轨道.成键轨道由于电子满占，根据能量最低原理和泡利不相容原理，成键轨道要向低能移动；反键轨道由于电子非满占或处于空轨道，该反成键轨道应向高能方向移动而性能所谓的能隙，且成键电子向电负性较大的H原子偏移.

图2 α-BeH2的能带结构Fig.2 The band structure of α-BeH2

G→GG→ZG→TG→YG→SG→XG→UG→R5 445 845 955 746 276 275 776 48Z→ZT→TY→YS→SX→XU→UR→R5 896 045 796 716 706 607 24

图3 α-BeH2沿(002)平面的差分态电荷密度图Fig. 3 Charge density along the (002) plane of α-BeH2

原子s电子p电子电荷总数净电荷H11 300 001 30-0 30H21 320 001 32-0 32Be10 241 131 370 63Be20 261 141 390 61

3.3 α-BeH2光学性质

在线性光学光学响应范围内, 通常用复介电函数ε(ω)=ε1(ω)+iε2(ω)来描述固体宏观光学响应函数，其中ε1(ω)为介电实部，ε2(ω)为介电虚部，通过占据态和非占据态波函数的动量矩阵元可得[23-25]：

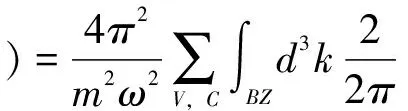
×δ[EC(k)-EV(k)-ħω]

(1)

表4 α-BeH2的Mulliken重叠布居数

(2)

其中P是动量矩阵元.其他光学性质，如反射率，折射率也可由介电函数的实部和虚部求出.具体关系式如下所示[23-25]：

折射率：

(3)

吸收系数：

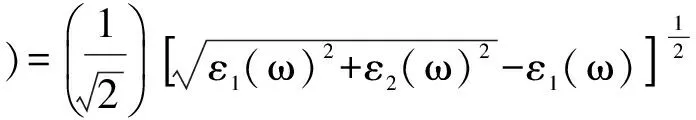
(4)

(5)

(6)

图4为α-BeH2介电函数的实部ε1(ω)和虚部ε2(ω).不考虑接近零点能位置的谱线变化情况，本征态介电函数虚部主要存在五个主跃迁峰，这五个主跃迁峰分别位于A(6.33eV)、B(6.95eV)、C(7.31eV)、D(7.88eV)和E(8.73eV)处，从能带和态密度分析可知A峰主要来自H1s态电子向Be2s态电子跃迁贡献；B峰起源于H1s 态电子向Be2s态电子，Be2p态电子向Be2s态电子跃迁；C峰来源于H1s电子向Be2s态电子跃迁；D峰由H1s态电子向Be2p态电子跃迁贡献；E峰起源于Be2p态电子向Be2s态电子跃迁.介电函数虚部ε2(ω)初始阈值E0=5.49eV接近平衡态时的能隙值(5.44eV).众所周知，当材料的禁带宽度大于3.1eV时[26,27]，材料对紫外光的吸收比较敏感，所以α-BeH2是一种优良的紫外光学材料.本征态介电函数实部ε1(ω)存在一个负值区域，即：7.48到13.01eV.说明α-BeH2在这些能量范围呈现出金属性质.零频情况时，静态介电函数实部ε1(0)为2.84.

图4 α-BeH2复介电函数实部ε1(ω)和虚部ε2(ω)Fig. 4 The real ε1(ω) and imaginary ε2(ω) parts of complex dielectric function of α-BeH2

图5为α-BeH2的光学吸收系数和光学吸收带边.吸收带边Eop可以由下列公式求得[28]：

αhυ=C(hυ-Eop)n

(7)

其中，hυ为光子能量，C为一常数，α为吸收系数.材料为直接带隙材料时，n=0.5；材料为间接带隙材料时，n=2.利用线性外推法计算得到α-BeH2的直接吸收边为6.16eV, 与前面计算得到的帯隙5.44eV相近.由于利用第一性原理中的局域密度近似(LAD)或广义梯度近似(GGA)交换关联能函数计算材料的带隙宽度偏低，因此我们预测利用线性外推法计算得到的吸收带边值更接近实验值.图5中的插图为α-BeH2光学吸收系数随能量的变化关系.吸收开始于5.50eV左右处，吸收强度随着能量的增加而增强，8.18eV时达到一最大值3.44×105/cm，之后总体减小到零.α-BeH2的主要吸收区域位于紫外区域，由此可知α-BeH2是一种优良的紫外光学材料.对于α-BeH2，当光子能量小于5.50eV或者小于其帯隙值时没有吸收发生，电子处于禁戎状态.图6为α-BeH2的复折射率n(ω)和消光系数k(ω)随能量的变化关系.零频情况下，静态折射率n(0)是一非常重要的物理量，α-BeH2静态折射率n(0)为1.68.最大复折射率位于6.22eV处，其值为3.14，此峰主要由Be2s 和2p态电子共同贡献.相比，α-BeH2的消光系数曲线与介电函数虚部ε2(ω)很类似.

图7为α-BeH2的能量损失谱L(ω)和反射谱R(ω).能量损失谱是描述快电子穿透材料时能量损失情况的重要物理参数.一般来说，能量损失谱L(ω)峰位可以用来表征材料中等离子体的共振情况，相对应的频率被称为等离子体共振频率[29].由图7可知，α-BeH2能量损失峰主要位于13.01eV处，其强度分别为357.28.零频情况下，α-BeH2的反射率为6.45%，且0到5.25eV能量区间，α-BeH2的反射率几乎相同，可以预测在红外和可见光区α-BeH2是一透明材料，且在这些能量范围α-BeH2可用作减反膜涂层材料.最大反射率出现在12.90eV处，其值为96.32%.当能量损失达到最大时，可以观察到α-BeH2反射率反而快速下降，如图7中虚线所示.

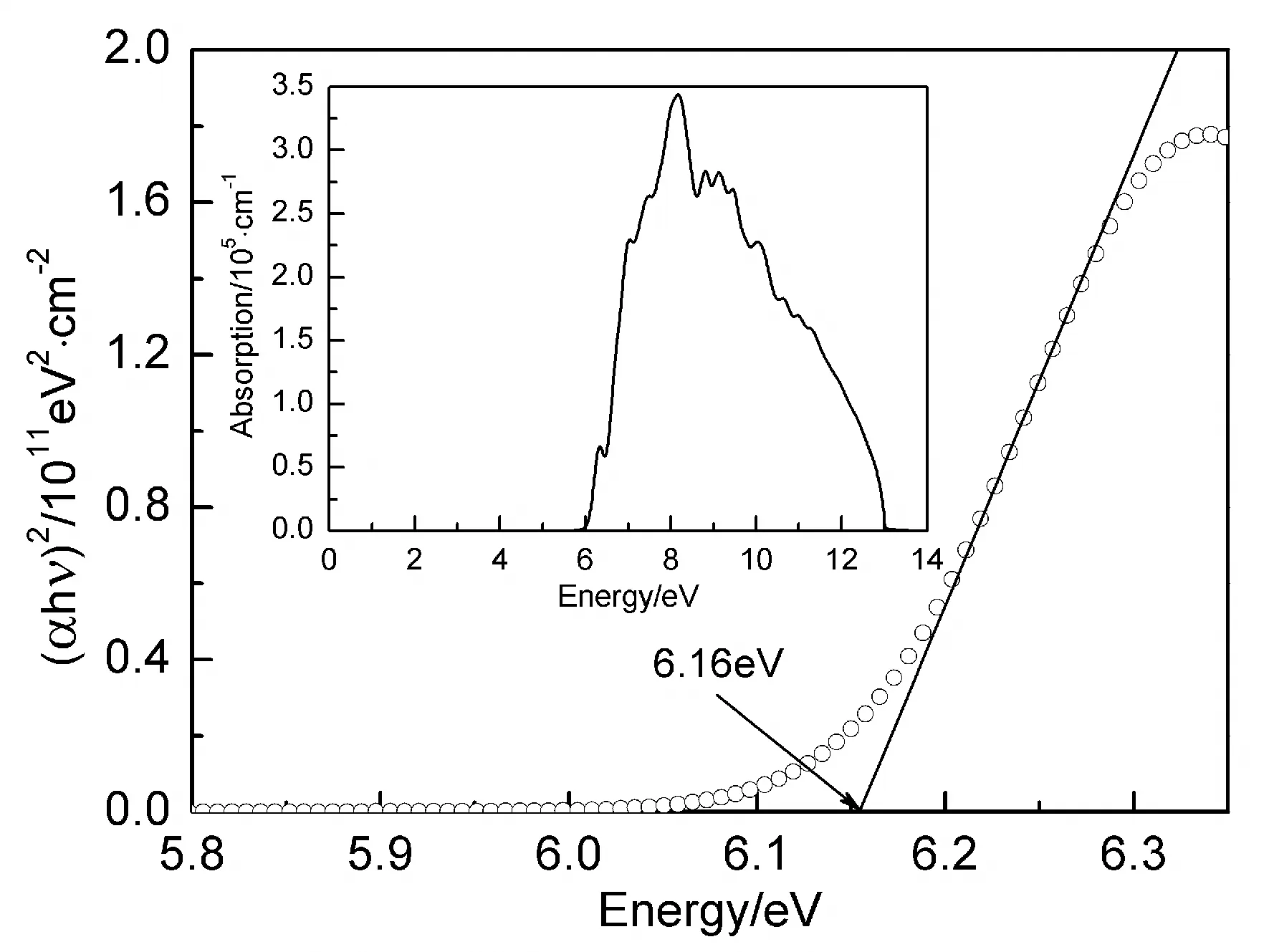
图5 α-BeH2光学吸收带边Eop和光学吸收系数I(ω)Fig. 5 The absorption edge Eop and optical absorption coefficient I(ω) of α-BeH2

图6 α-BeH2复折射率n(ω)和消光系数k(ω)Fig. 6 The complex refractive index n(ω) and the extinction coefficient k(ω) of α-BeH2

图7 α-BeH2能量损失谱(a)和反射率(b)Fig. 7 Optical spectra as a function of photon energy for α-BeH2: (a) energy loss function and (b) reflectivity

4 结 论

基于密度泛函理论(DFT)，采用赝势平面波方法和广义梯度近似(GGA)计算研究了α-BeH2的结构、电子和光学性质.α-BeH2为直接能隙半导体材料，其能隙为5.44eV，通过对基态α-BeH2的Mulliken电荷布居分析和重叠布居数分析发现：α-BeH2属于离子键和共价键所形成的混合键化合物；α-BeH2的电荷总数分别来源于各自的H1s轨道，Be2s和2p轨道.同时本文还研究分析了α-BeH2的光学介电函数、吸收系数、复折射率、反射系数和能量损失等光学性质.α-BeH2的主要吸收区域位于紫外区域，α-BeH2是一种优良的紫外光学材料.

[1]SeninMD,AkhachinskiiVV,MarkushkinYE.Theproduction,structureandpropertiesofberylliumhydride[J].Inorganic Materials, 1993, 29: 1416.

[2]SampathS,KolesnikovAI,KristinaML, et al.Vibrationaldynamicsofamorphousberylliumhydrideandlithiumberylliumhydrides[J]. J. Chem. Phys., 2008, 128: 134512.

[3]SalKF, Ed.HuaXS,HuoHS,TaoYZ, et al. Tran. Present situation and prospect of inertial ionfinement fusion[M].Beijing:AtomicEnergyPress, 2008: 39(inChinese)[萨尔柯夫主编. 华欣生, 霍广盛, 陶益之等译. 惯性约束核聚变现状与能源前景[M]. 北京： 原子能出版社，2008: 39]

[4]Gus'kovSY,ZmitrenkoNV,MarkushkinYE, et al.Energeticefficiencyoflaserthermonucleartargetswithablatorshellsmadeofberylliummaterials:Acomparativeanalysis[J]. J. Russ. Laser. Res., 2007, 28:148.

[5]BarbarasGD,DillardC,FinholtAE, et al.Thepreparationofthehydridesofzinc,cadmium,beryllium,magnesiumandlithiumbytheuseoflithiumaluminumhydride[J]. J. Am. Chem. Soc., 1951, 73: 4585.

[6]CoatesGE,GlocklingF.Di-tert.-butylberylliumandberylliumhydride[J]. J. Chem. Soc., 1954, 2526.

[7]HeadEL,HolleyJrCE,RabideauSW.Di-t-butylberylliumandberylliumhydride[J]. J. Am. Chem. Soc., 1957, 79: 3687.

[8]MarkhushkinYF,ChirinNA.Berylliumdeuteride-tritideasfuelforICFtarget[J]. J. Moscow Phys. Soc., 1999, 9: 77.

[9]VajeestonP,RavindranP,KjekshusA, et al.StructuralstabilityofBeH2athighpressures[J]. Appl. Phys. Lett., 2004, 84: 34.

[10]HohenbergP,KohnW.Inhomogeneouselectrongas[J]. Phys. Rev., 1964, 136(3B):B864.

[11]SegallMD,LindanPJD,ProbertMJ, et al.First-principlessimulation:ideas,illustrationsandtheCASTEPcode[J]. J. Phys.: Condens. Matter, 2002, 14: 2717.

[12]PerdewJP,BurkeK,ErnzerhofM.Generalizedgradientapproximationmadesimple[J]. Phys. Rev. Lett., 1996, 77: 3865.

[13]MilmanV,WinklerB,WhiteJA, et al.Electronicstructure,properties,andphasestabilityofinorganiccrystals:Apseudopotentialplane-wavestudy[J]. Int. J. Quantum Chem., 2000, 77: 895.

[14]MonkhorstHJ,PackJD.SpecialpointsforBrillouin-zoneintegrations[J]. Phys. Rev.B, 1976, 13:5188.

[15]PfrommerBG,CoteM,LouieSG, et al.Relaxationofcrystalswiththequasi-Newtonmethod[J]. J. Comput. Phys., 1997, 131: 233.

[16]MurnaghanFD.Thecompressibilityofmediaunderextremepressures[J]. Proc. Natl. Acad. Sci. USA, 1944, 30: 244.

[17]SimthGS,JohnsonQC,SimthDK, et al.Thecrystalandmolecularstructureofberylliumhydride[J]. Solid State Commun., 1988, 67(5): 491.

[18]VisputeRD,TalyanskyV,ChoopunS, et al.HeteroepitaxyofZnOonGaNanditsimplicationsforfabricationofhybridoptoelectronicdevices[J]. Appl. Phys. Lett., 1998, 73: 348.

[19]LinZ,OrlovA,LambertRM, et al.Newinsightsintotheoriginofvisiblelightphotocatalyticactivityofnitrogen-dopedandoxygen-deficientanataseTiO2[J]. J. Phys. Chem.B, 2005, 109: 20948.

[20]MullikenRS.ElectronicpopulationanalysisonLCAO-MOmolecularwavefunctions.I[J]. J. Chem. Phys., 1955, 23: 1833.

[21]SegallMD,PickardCJ,ShahR, et al.Populationanalysisinplanewaveelectronicstructurecalculations[J]. Mol. Phys., 1996, 89: 571.

[22]SegallMD,ShahR,PickardCJ, et al.Populationanalysisofplane-waveelectronicstructurecalculationsofbulkmaterials[J]. Phys. Rev.B, 1996, 54:16317.

[23]Ambrosch-DraxlC,SofoJO.Linearopticalpropertiesofsolidswithinthefull-potentiallinearizedaugmentedplanewavemethod[J]. Comput. Phys. Commun., 2006, 175: 1.

[24]FoxM. Optical properties of solids [M].NewYork:OxfordUniversityPress, 2001.

[25]WootenF. Optical properties of solids [M].NewYork:Acadmicpress, 1972: 179.

[26]MaqboolM,AminB,AhmedI.BandgapinvestigationsandtheeffectoftheInandAlconcentrationontheopticalpropertiesofInxAl1-xN[J]. J. Opt. Soc. Am.B, 2009, 26: 2181.

[27]MaqboolM,KordeschME,KayaniA.EnhancedcathodoluminescencefromanamorphousAlN:holmiumphosphorbyco-dopedGd+3foropticaldevicesapplications[J]. J. Opt. Soc. Am.B, 2009, 26: 998.

[28]SrikantV,ClarkeaDR.OpticalabsorptionedgeofZnOthinfilms:Theeffectofsubstrate[J]. J. Appl. Phys., 1997, 81: 6357.

[29]AndersonOL.AsimplifiedmethodforcalculatingtheDebyetemperaturefromelasticconstants[J]. J. Phys. Chem. Solid, 1963, 24: 909.

First principles study of electronic and optical properties of α-BeH2

PENG Min1, WEI Jian-Jun2, ZHANG Ji1, LIU Li1,2

(1. Basic Department, Xin Jiang Institute of Engineering, Urumqi 830091, China；2. Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China)

The structural, electronic and optical properties of α-BeH2were investigated using the pseudo-potential plane wave method within the generalized gradient approximation in the frame of the density functional theory. The ground state properties, such as lattice constant a and bulk modulus B0, were calculated. These results are in good agreement with the experimental and other theoretical data. According to the band structural theory, we have studied the band structure, density of states (DOS) and partial density of states (PDOS) for α-BeH2at the ground state. We found that α-BeH2is a direct band gap semi-conductive material with the band gap 5.44 eV. The result is smaller than that in literature. This is because in response to the band gap or magnetic coupling theory, the calculated results using the local density approximation (LDA) or generalized gradient approximation (GGA) within the first principles are smaller than those using other method. We investigated the Mulliken charge and population of α-BeH2. It is indicated that α-BeH2is a mix bond chemical compound consisting of ionic bond and covalent bond. The total charge of α-BeH2derives from H 1s, Be 2s and 2p orbits, respectively. At the same time, the dielectric function, adsorption coefficient, refractive index, reflection coefficient and loss function of α-BeH2were calculated and investigated.

First principles; α-BeH2; Optical properties; Dielectric function

彭敏(1978—)，女，新疆乌鲁木齐人，硕士，讲师，主要从事电气自动化控制与技术研究.

韦建军.E-mail: wjj33333@163.com

103969/j.issn.1000-0364.2015.08.023

O443.5

A

1000-0364(2015)08-0653-07

投稿日期: 2014-09-07